基于Logistic回归对过敏性疾病影响因素的计量分析

徐 香，蒋 娟，朱家明

(1.安徽蚌埠第四人民医院,安徽 蚌埠 233010;2.兰州大学,甘肃 兰州 730000；3.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

十九大报告提出“要像对待生命一样对待生态环境，保护好生态环境就是保护未来”。生态环境的不断恶化，会导致一系列空气污染等现象的发生，例如PM2.5浓度增高，会导致各类过敏性疾病的发生，譬如皮肤过敏、呼吸道过敏、消化道过敏等。过敏性疾病是机体因变态反应而出现的临床表现各异的一类免疫反应性疾病，包括过敏性鼻炎、支气管哮喘、荨麻疹、过敏性结膜炎等[1],且从新生儿到老年人的各个年龄阶段都可能发生，往往具有明显的遗传倾向。在过敏性疾病中，以速发型过敏反应比较常见，其主要类型有皮肤过敏反应、呼吸道过敏反应、消化道过敏反应及过敏性休克[1]。本文通过对过敏性疾病的相关影响因素分析，为预防过敏反应及过敏性疾病的治疗提供可靠依据，从而有效降低过敏性疾病发病率。同时结合相关生态环境指标，分析生态环境对过敏性疾病发病率的影响，为相关政府部门和广大市民朋友提供合理的建议。

1 模型假设及文献综述

1.1 数据来源及假设

数据来源于中国医学临床案例。为便于解决问题，提出以下假设：⑴假设数据中儿科、耳鼻喉科、呼吸科和皮肤科的患者均是由于自身患有过敏性疾病而进行过敏原检测；⑵假设数据给出的过敏程度可以近似取整，如过敏程度“5(4+)”可近似等于“5”。

1.2 文献综述

刘妍妍等[2]应用Hurdle模型分析了具有零膨胀数据阳性过敏原数的影响因素，为预防过敏反应及过敏性疾病提供依据。罗宇阳等[3]通过采用Logistic回归分析法探讨了南宁市0～24个月婴幼儿过敏性疾病的临床特征及相关影响因素。崔一帆等[4]采用单因素分析以及Logistic回归，分析儿童过敏性鼻炎的危险因素，得出2016年来院就诊儿童过敏性鼻炎排名前五位的过敏原。以上研究通过采用不同方法，得出过敏性疾病的相关影响因素并且为过敏反应的预防提供依据。G Melioli等[5]通过对不同年龄段过敏性疾病患儿的横截面研究显示，食物过敏原特异性IgE(免疫球蛋白E)在幼儿出生早期(2岁以内)即可从血清检出，其主要为牛奶和鸡蛋，而后期吸入性过敏原特异性IgE逐渐出现且稳定。S.P.Nissen等[6]发现婴儿早期食物过敏原的致敏率最高，而后期吸入占据主要地位[7]。以上研究均发现过敏原随年龄而变化的规律，且在血清特异性IgE[8]这个I型速发过敏反应的标志物上发生变化。

1.3 数据处理

(1)科室分类。通过查阅相关医学文献，将原数据表中科室类别重新分为：儿科、呼吸科、耳鼻喉科、皮肤科、其他科[9]。

(2)设置其他过敏原。对于前来问诊但致病过敏原未知的病人，设置其他过敏原项。

(3)对过敏疾病分类。首先将所给某医院过敏原检测数据依据科室这一指标进行过敏性疾病类型的分类，根据各科室的所占权重大小将过敏性疾病分成5类：儿科、耳鼻喉科、呼吸科、皮肤科以及其他科，由公式pi=ni/∑ni， 可计算出各科室出诊频率分别为：儿科0.074，耳鼻喉科0.076，呼吸科0.275，皮肤科0.375，其他科0.2。

(4)对性别的处理。由于性别只有男和女两种情况，故将性别设置为虚拟变量，引入0/1，将男性患者设为1，女性患者设为0。

(5)对季节的处理。将一年四个季节引入春、夏、秋这3个虚拟变量，并设置具有该性质为1，否则为0。

(6)对过敏原检测结果处理。因数据来源中未对调查结果作出明确解释，根据检测的IgE浓度[10]，可将0～6级过敏原转换为具体分数，见表1。

表1 特异性浓度对应级别

(7)对年龄处理。将年龄段按5年作为组距，将2 284名过敏患者按组分为20组，分别统计每组患者数。

2 定性分析

2.1 研究思路

(1)将4年的就诊数据按照365为量度，使日期数据转化为一年中对应的天数，作为时间对过敏性疾病影响因素的相关数据；(2)将科室分为5类科室，按照季度，分别对每个科室的就诊量进行计数，作为季节影响的数据基础；(3)统计各科室的男女就诊情况的数据，作为性别影响因素的数据基础；(4)用20组分类的年龄数据分别对不同科室的就诊量进行计数，作为年龄影响因素的相关数据。通过运用Excel、MATLAB等绘制不同类型过敏性疾病与各影响因素之间的散点图、柱状图等，根据所得结果进行描述性分析。

2.2 研究方法及结果分析

(1)过敏性疾病与时间的相关关系

运用MATLAB对所收集的数据进行初步处理，把日期时间通过365天/年的刻度单位化作为x轴，将就诊病人的年龄作为y轴绘出5类科室出诊次数散点图，如图1所示。

图1 各科室出诊频率分布散点

由图1可知，耳鼻喉科和呼吸科在0～50 d、250～365 d之间出诊频率较高，在100～250 d之间较低。总体上而言，过敏性疾病发病频率夏季与秋冬对比，在夏季明显降低。

(2)过敏性疾病与季节的相关关系(图2～3)

图2 不同季节各科室出诊次数 图3 不同季节各科室出诊频率

由图2可知，全年各季节皮肤科就诊人数相较于其它科室最多，耳鼻喉科最少。在春夏交替之时，由于草木生长以及花粉的传播，呼吸科就诊的人数明显呈现上升趋势；在秋冬交替之时，就诊人数呈现下降趋势。其余科室就诊人数全年无明显波动变化。由图3可知，夏季过敏性疾病发病率明显高于冬季，春秋无明显区别。可以看出，皮肤科就诊人数比例在5个科室中占比最高且四季无明显波动。

(3)过敏性疾病与性别的相关关系(图4)

图4 各科室男女就诊人数

由图4可知，男性与女性在皮肤科方面的过敏性疾病发病人数有较大差别，女性更加容易患上皮肤性过敏疾病。同时可以看出其余4种科室出诊次数无明显波动。

(4)过敏性疾病与年龄的相关关系(图5)

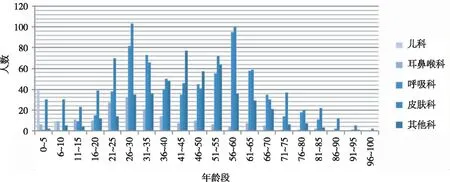
图5 各科室各年龄段就诊人数

由图5可知，婴幼儿时期更加容易患上过敏性疾病，青少年时期发病率较低。在26～30、56～60年龄段之间更加容易患上皮肤性过敏疾病，年龄的大小与过敏性疾病存在一定的相关关系。横向对比来看，耳鼻喉性过敏性疾病发病率在不断上升(例如鼻炎)，皮肤过敏性疾病发病率最高，其次是呼吸道过敏疾病。

3 定量分析

3.1 研究思路

剔除科室就诊结果为空的数据，对不同的科室进行分类，建立解释变量时间、季节、性别与被解释变量科室之间的函数关系。将皮肤科设为参考类别、性别以及季节作为因子、年龄作为协变量，建立多分类的Logistic回归模型并求出模型，并以二元Logit回归对儿科相关变量之间的关系进行检验。运用SPSS和Eviews进行求解，通过对运行结果的分析，得出过敏性疾病与时间、季节、性别等之间的逻辑回归方程并作出合理的解释说明和相互论证。

3.2 研究方法

多分类Logistic回归模型。对于K个可能的分类结果，运行K-1个独立二元逻辑回归模型，在运行过程中把其中一个类别看成是主类别，然后将其它K-1个类别和我们所选择的主类别分别进行回归。通过这样的方式，如果选择结果作为主类别，可以得到以下公式

(1)

对公式(1)左右两边进行指数化处理得到

Pr(Yi=1)=Pr(Yi=K)eβ1xi,Pr(Yi=2)=Pr(Yi=K)eβ2xi,…,Pr(Yi=K-1)=Pr(Yi=K)eβK-1xi

(2)

其中βi(0<βi<1)为第i个变量的系数，得到的概率必须加起来等于1，基于这个事实可以得到

(3)

将式(3)带入到式(2)即可得到最终的结果表达式

(4)

对季节、性别、年龄分别引入0/1变量，且输出类别为儿科：1，呼吸科:2，耳鼻喉科:3，皮肤科:4，其他科:5。为保证xi与输出结果Pr(Yi)的一一对应关系，在式(4)右边xi乘以Yi，得到模型，见式(5)。

(5)

3.3 结果分析

根据上述分析，运用SPSS，分别以各发病频率代替各过敏性疾病类型，并将其作为因变量，参考类别为皮肤科；将性别以及春、夏、秋3个虚拟变量作为因子；由于患者的年龄作为一个独立变量，不受人为控制，但其数值仍影响着患病结果，所以将年龄作为协变量。进行多元Logistic回归，结果见表2。

表2 拟合优度表

由表2可知，原假设模型能很好地拟合原始数据，最后一列皮尔逊卡方显著性值0.996概率较大，原假设成立，说明模型对原始数据的拟合通过检验。根据极大似然比检验表，我们能看到最终进入模型的效应包括截距、年龄、性别、季节，而且最后一列显著性值均小于0.05，表明自变量对模型构成均有显著贡献，故根据参数估计值表得出如下模型：

W1=log[p(儿科/皮肤科)]=4.32-0.428x1-0.177x2-0.455x3-0.326x4-0.35x5W2=log[p(耳鼻喉科/皮肤科)]=1.749-0.186x1-0.837x2-0.077x3-0.827x4-0.033x5W3=log[p(其他科/皮肤科)]=0.963-0.496x1-0.79x2-0.940x3-0.459x4-0.007x5W3=log[p(呼吸科/皮肤科)]=-0.354-0.2x1-0.185x2+0.075x3-0.234x4-0.009x5

4 定量分析2013-2017年过敏原检测结果的变化趋势

4.1 研究思路

首先，运用Excel对数据进行初步处理，汇总2013-2017年每年就诊病人中各类过敏原致病人数，再利用MATLAB多元回归工具箱作出每一类由过敏原致病人数随时间变化的多元回归方程，并作出R2检验。通过查阅大量文献资料，将17种过敏原按照生态环境的因素进行科学的分类，分为土壤类致病过敏原、空气类致病过敏原、水资源类致病过敏原。随后，按照过敏原的三大类分别找取与之对应的三大类环境指标，并利用相关系数进行判断，挑选出与之相关性程度最高的环境类指标。最后，运用灰度预测模型预测未来几年各类过敏原发病率及环境因素，再次求出两者间的相关系数，检验是否依然存在合理可靠的相关关系。

4.2 研究方法

过敏原检测结果变化趋势。利用Excel进行统计分析，考虑到过敏程度，我们采用求和的方式，统计汇总得出2013-2017年就诊病人中各类过敏原致病人数，并由此得出各类过敏原致病人数随时间变化的多元回归模型并给出检验系数。具体结果见表3。

表3 过敏原变化趋势拟合方程

环境保护指标的选取。根据查阅的大量文献资料进行综合考虑，将17种过敏原按受生态环境影响因素进行科学的分类[11]，最终分为土壤类致病过敏原、空气类致病过敏原、水资源类致病过敏原3类。具体分类结果见图6。

图6 致病过敏原分类结果

通过查阅环境保护文献分别选取2个土壤类环境保护指标：污水排放总量、降水量；2个空气类环境保护指标：烟粉尘排放总量、PM2.5；1个水资源类环境保护指标：废水主要污染物排放量。查阅相关数据结果见表4。

表4 环保指标数据

将5个环境指标分别与过敏原指标进行相关分析，得出污水排放总量与大多数过敏原检测结果相关，故选取污水排放总量这一环境保护指标进行相关分析。

相关性分析：将过敏原指标和环保指标进行标准化处理，用相关系数法求得两者之间的相关性见表5。

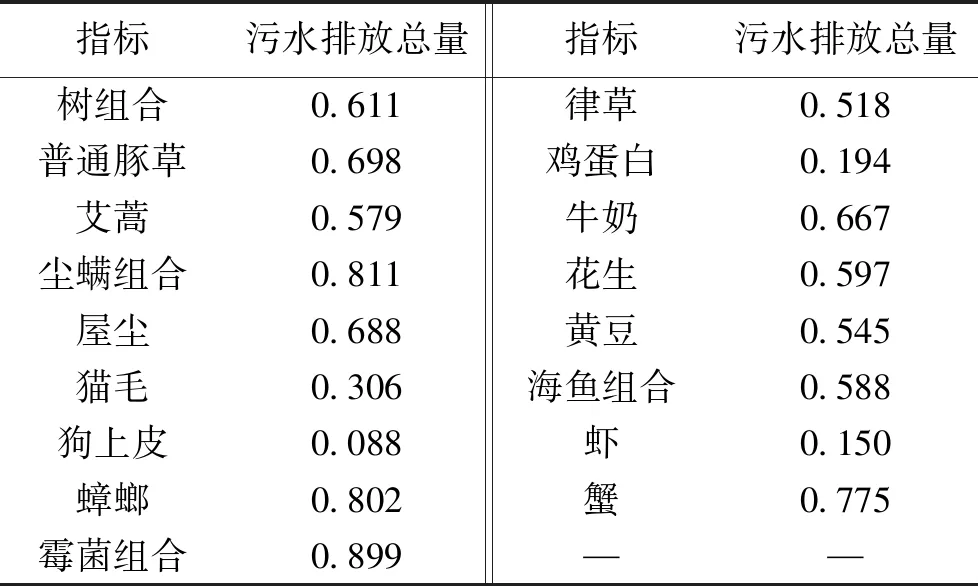
表5 相关系数

分析可知，除了猫毛、狗上皮、鸡蛋白和虾以外，污水排放总量这一指标与其余13个过敏原指标之间均呈现较强的正相关关系。

4.3 模型的检验

根据2013-2017年的相关数据，利用灰色预测法预测出2018年过敏原各项指标和5项环保指标，如见表6。

表6 2018年数据预测

根据2018年数据预测表，用2013-2018总计6年的数据做回归分析和相关关系矩阵的求解，得到的结果可以看出，预测结果与原来结果具有一致性。

5 结语与建议

多分类的Logisitic回归在医学领域有着及其重要的地位和影响力。本文采用定量与定性相结合的方法，运用医学领域常用的多分类Logistics回归模型进行分析，提高了所求变量间相关性的准确程度[12]。根据过敏程度评分标准，我们将过敏等级(1-6)转化为检测得分(1-100分)，使得原始变量变为连续性变量，有效区分了不同过敏程度之间的差异性，使得结果更加准确合理。运用SPSS，Eviews，MATLAB等多种数学软件进行计算，取长补短，使计算结果更加准确[13]。基于过敏原多影响因素分析模型的推广，将时间、季节、年龄、性别与过敏原致病类别进行逻辑回归，得到了两两间的定量相关关系，对今后分析不同类型疾病的病人过敏原检测结果之间的差异及环境对致病概率的影响提供了理论基础[14]。