一种基于遗传算法的通信网拓扑优化方法*

尹梦梦，王 磊，姚昌华，童 玮

（1.陆军工程大学，江苏 南京 210001；2.南京信息工程大学，江苏 南京 210044）

0 引言

通信网[1]的网络结构（即网络拓扑）是泛指网络节点和传输线路的几何连接形状，关系着网络连通性问题[2]。从网络的内部结构属性出发，探究具有较高可靠性的通信网，在各种实际应用中是一项重要需求。

目前，关于通信网可靠性的研究已取得了不少成果。文献[3]提出了实现导航共享的通信网络拓扑优化方法，为寻找不同条件下具有最小通信连接数（Minimum of Communication Connections Number，MCCN）的通信网络拓扑建立了导航共享的MCCN 拓扑模型，并设计了相应方法，理论上证明了算法的有效性。文献[4]提出了一种基于服务特性和节点可靠性的电力通信网络故障恢复算法，通过与传统算法的比较，验证了该算法提高了电力通信网络的故障恢复率和收益，具有很大的实际应用价值。文献[5]利用FCM 算法对电力通信网的关键资源进行识别和备份，从而提升了电力通信网的可靠性。文献[6]以复杂网络为研究对象，建立了基于冗余度的网络可靠性及节点重要度评估模型。结果表明，该模型算法能为一定约束成本限制下高可靠性网络的构造问题提供解决方案。

本文从通信网拓扑结构的角度构建可靠性优化模型。该模型属于NP-hard 问题，直接求解难度大。本文针对目标函数设计了改进的遗传算法求解该模型，是一种启发式方法。编码过程即网络转化为邻接矩阵的过程，设计的优化变量是以图的邻接矩阵形式进行编码。选用轮盘赌、截断和排序分组3 种选择操作，使用单点交叉算子在交叉位进行交叉操作，采用单点变异的变异操作。通过仿真实验，验证了本算法能有效提升通信网的可靠性。

1 基于自然连通度的通信网可靠性优化模型

本文以自然连通度作为网络可靠性测度指标优化其拓扑结构。

对通信网图G的基本假设如下。

（1）通信网是无权图且为无向简单图，因此aij的取值集合为{aij=aji=1|e(vi,vj)∈E(G)}和{aij=aji=0|e(vi,vj)∉E(G)}。

（2）满足连通图，即其拉普拉斯矩阵的次小特征根μ＞0。当网络规模增大时，次小特征根求解时间过长。为了简便处理，本文定义函数：

C(G)通过深度优先搜索为每一个节点进行遍历，遍历所有节点其结果都能连通任意其他节点。所的图即为连通图，否则为非连通图。

定义自然连通度，即假设在一个网络中，任意节点vi和vj之间的长度为k的途径数目为，然后通过i、j、k的关系求和：

S值的大小反映了网络中冗余路径数量的多少。显然，S将是一个复杂的表达式，采用起点和终点为长度为k的闭途径数目表示如下：

将S除以节点间长度为k的阶乘来衡量闭路径的贡献，其中较短的闭路径对替代路径的冗余性影响较大，表示如下：

此时，nk表示网络中所有长度为k的闭途径数目，可表示为：

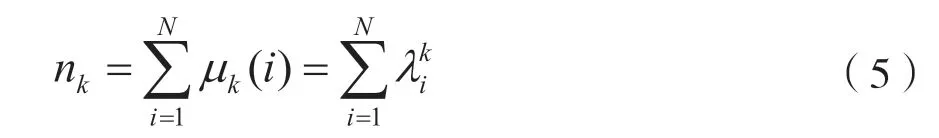
代回式（4），可得：

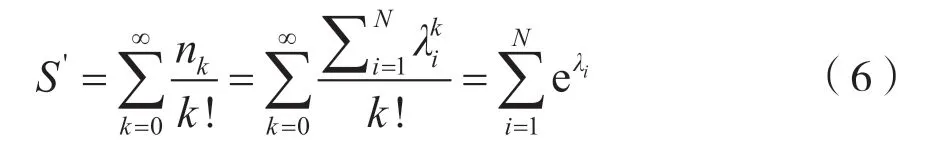
式中，λi代表该网络邻接矩阵的特征根。

影响网络可靠性的因素很多。在网络节点数量一定的情况下，网络中链路数量成为主要影响因素。自然连通度值关于增边是严格单调递增的，在对网络链路数量没有限制的情况下，全连接网络拓扑将是可靠性最优的网络。但是，事实上，网络构造会受到成本等限制，显然链路数越多的网络成本也将越大。因此，在链路数W一定的情况下，研究网络可靠性问题是必要的。本文假设通信网链路数量满足的约束条件如下：

由上述分析可建立通信网拓扑结构优化模型：

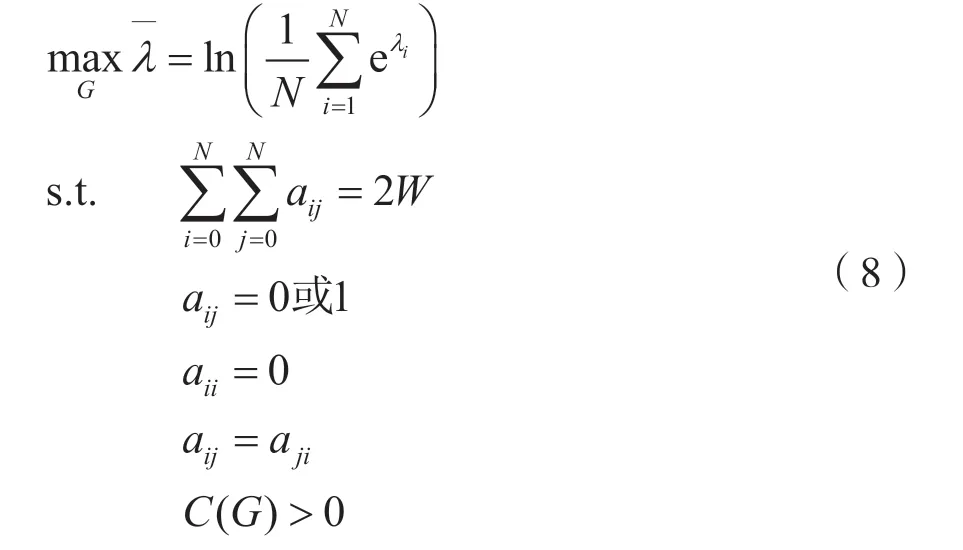
式中，λi为以aij组成的邻接矩阵A(G)的特征根。

2 基于遗传算法的通信网可靠性仿真优化方法

上述模型属于非线性0-1 整数规划问题，是典型的NP-hard 问题，无法使用目前的一些求解器直接进行求解。传统解决NP-hard 问题的方法包括使用相似问题替代原问题，即原问题复杂难求，不能直接求解，寻找相似度高且易于求解的问题进行替代。另一种方法是利用启发式搜索。本文优先选择群智能算法。由于网络图的邻接矩阵为0-1 矩阵，为了编码方式的便捷性，本文选择遗传算法进行问题的搜索，流程如图1 所示。

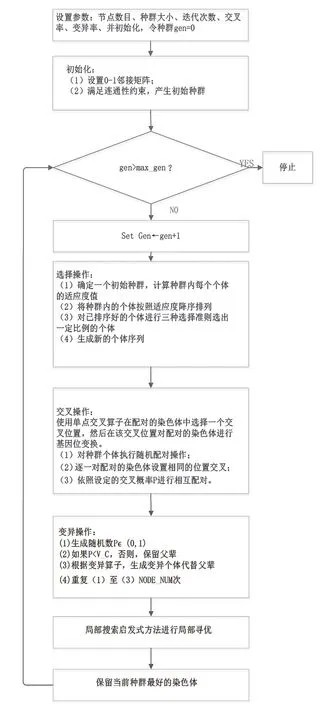
图1 遗传算法流程

2.1 变量编码

通信网可表示为无权、无向简单图，而图本身可以用0-1 邻接矩阵表示，很合适将其直接当做染色体。因此，每个邻接矩阵为遗传算法的优化变量，即解的编码。

2.2 选择操作

为了寻找可靠性更高的通信网拓扑结构，在每一次选择操作中依据目标函数值选择结果较大的个体。本文中分别选用轮盘赌选择、截断选择法、排序分组3 种不同的操作进行对比与分析。

截断选择法根据目标函数值大小对种群中的个体进行降序排列（求解max），选取前n个个体进入下一代，算法操作如下：

（1）在初始种群中计算每个个体（邻接矩阵）的目标函数值；

（2）按照适应度值大小进行降序排列；

（3）截取前n个最好的个体进入下一代。

排序分组选择的思想用图形表示如下。

（1）以个体数为9 的一个初始种群为例，表1中数据为种群个体适应度值。

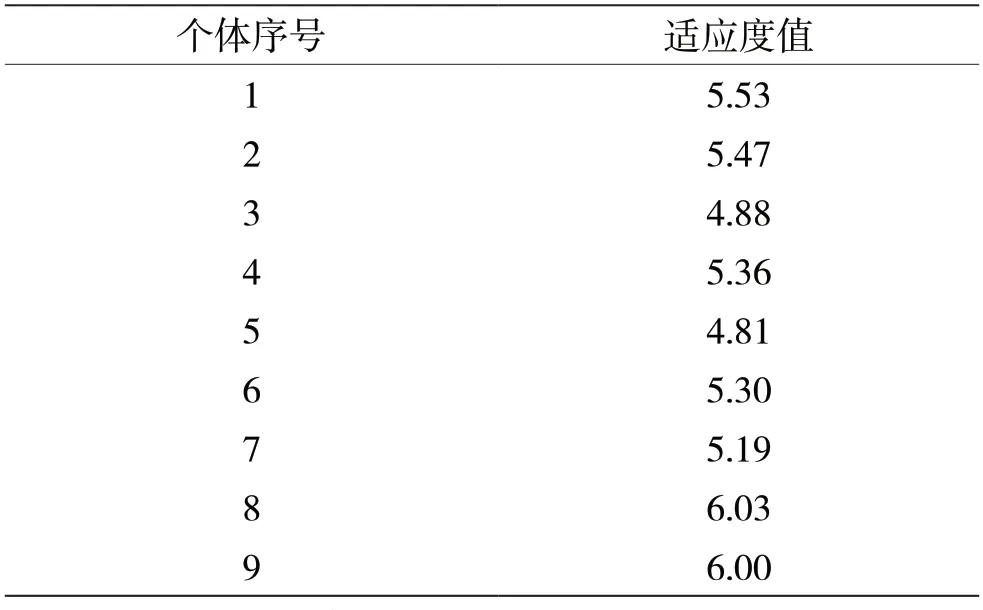
表1 个体数为9 的一个初始种群的个体适应度值

（2）种群个体按适应度值由大到小进行排列，如表2 所示。

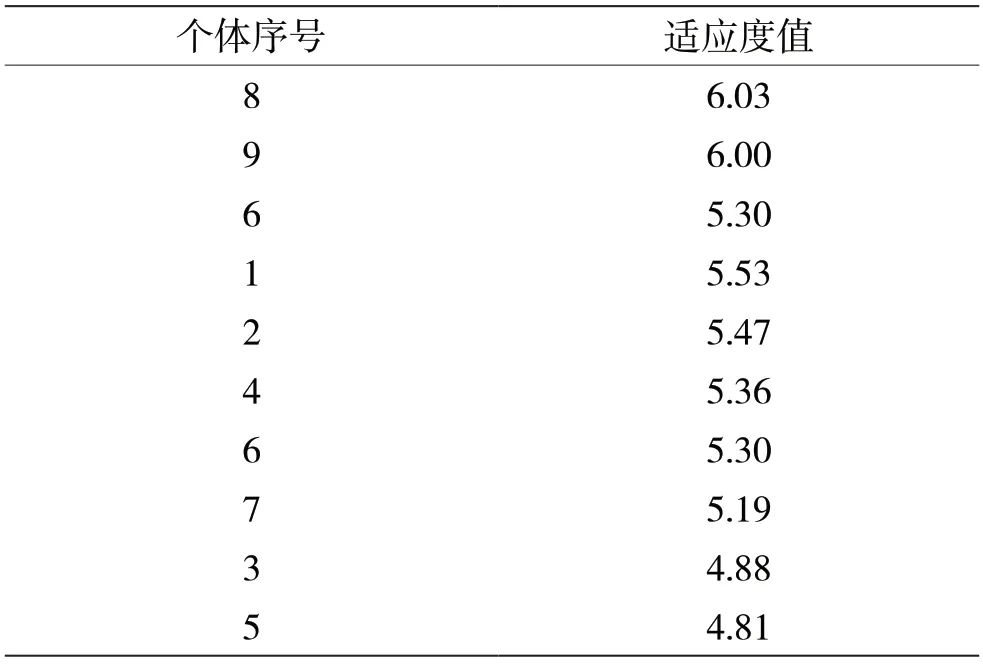
表2 适应度值由大到小进行排列的结果

（3）排列好的个体平均截取3 段。

（4）每段分别按不同的比例进行随机选择。

（5）选择出来的个体如表3 所示。

表3 选择出来的个体情况

（6）从头段中选取由于选择操作而损失的个体。

（7）将第（3）步选出的头部个体插入第（5）步中组合成新的个体，结果如表4 所示。

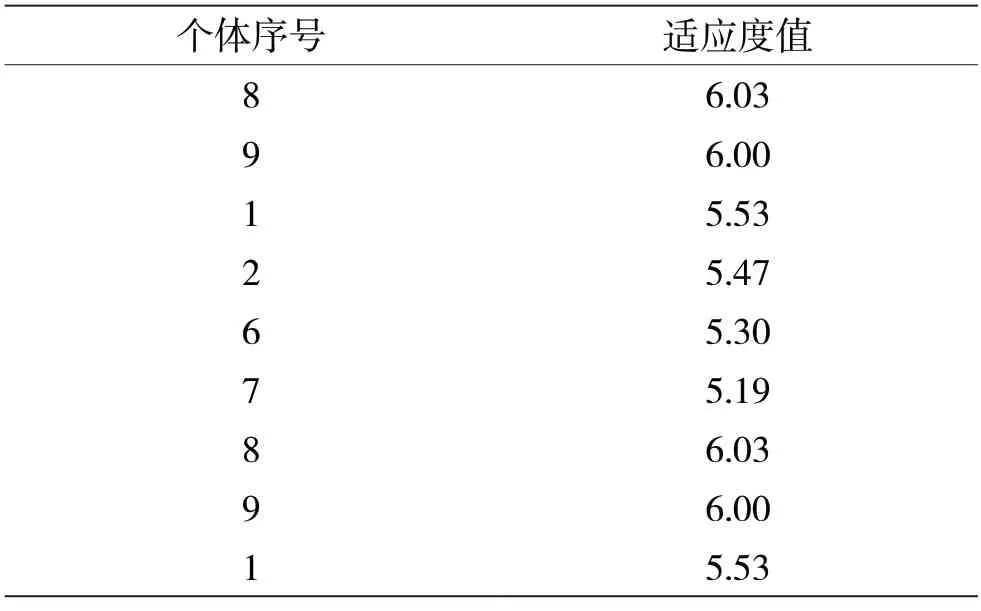
表4 选择出来的个体情况

最终种群与初始种群相比，平均适应度值都得到了提高。本文选用的3 种选择算法操作简便，在计算出适应度值后只需进行排序、分组、插入等一些基本的操作可选出较优个体。

2.3 交叉操作

选取不同的邻接矩阵交换矩阵中间元素实现在该交叉位置对其进行基因位变换，具体操作步骤 如下：

（1）对种群个体进行随机配对操作；

（2）针对配对的染色体设定相同的位置交叉点；

（3）依照设定的交叉概率P进行相互配对。

交叉过程如图2 所示。

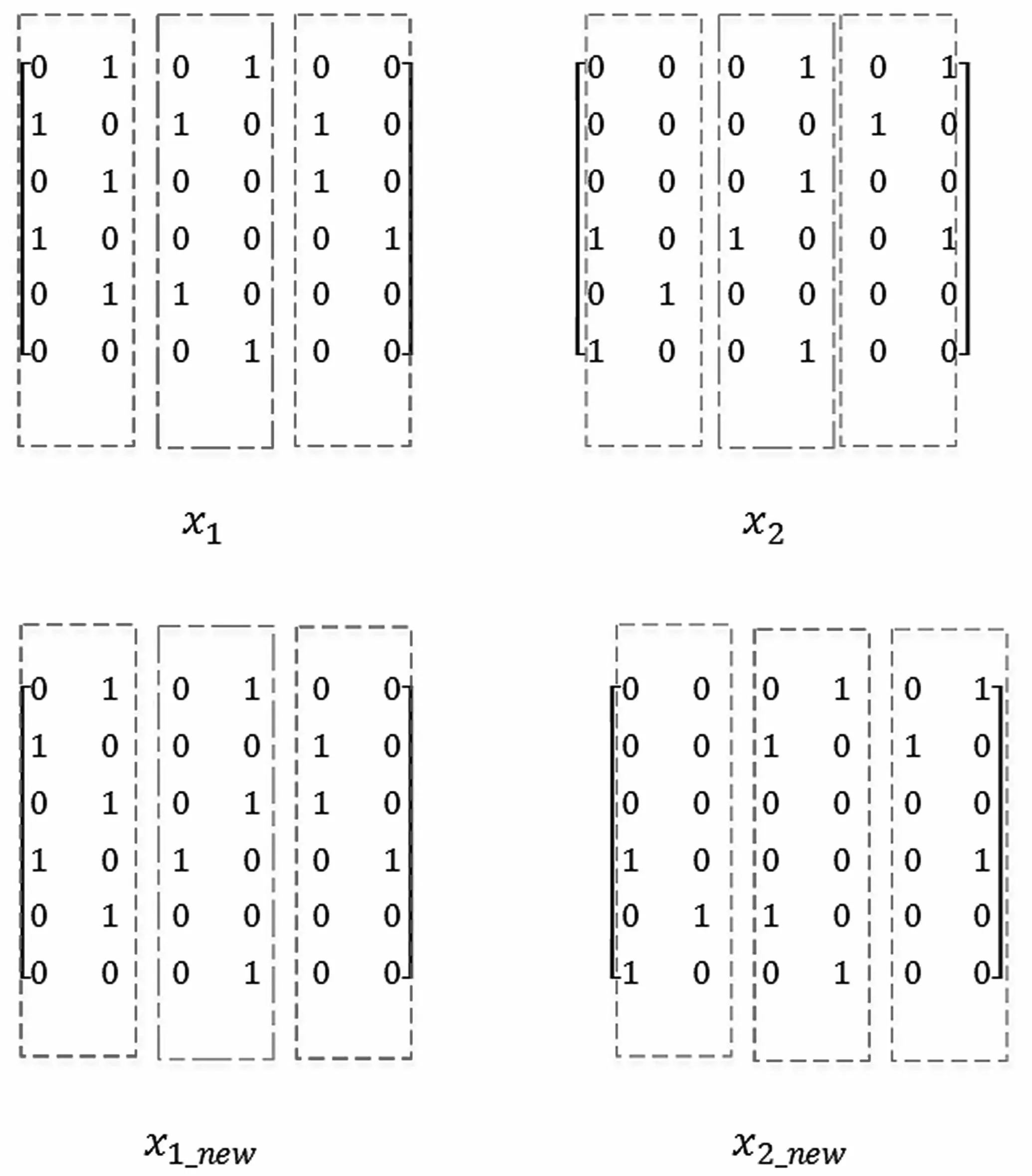
图2 交叉过程

2.4 变异操作

本文主要采用单点变异，即只需要对基因序列中某一个位进行变异。以二进制编码为例，即0 变为1，1 变为0。变异是从种群中随机选择个体按一定概率变异得到新个体的过程。例如，对某个个体进行变异，方法如下：

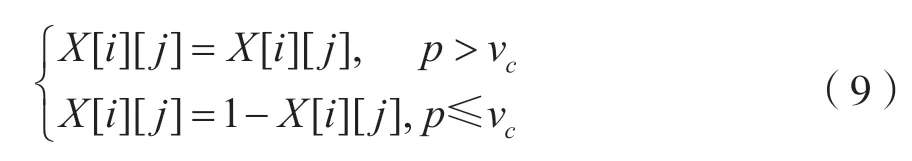
式中，X[i][j]为邻接矩阵中某一元素，p是位于[0，1]之间的随机数，vc是变异概率。

3 算法改进及模型约束

3.1 算法改进

传统的遗传算法容易出现收敛速度慢的问题，本文改进了局部寻优策略，具体如下。

3.1.1 局部搜索

在每一次迭代结束后，对种群中的每一个染色体进行局部搜索优化。局部搜索具体操作为对当前染色体所表示的邻接矩阵的任意一位取反操作，可表示为函数N(Gk)。局部搜索对染色的更新具体表示为：

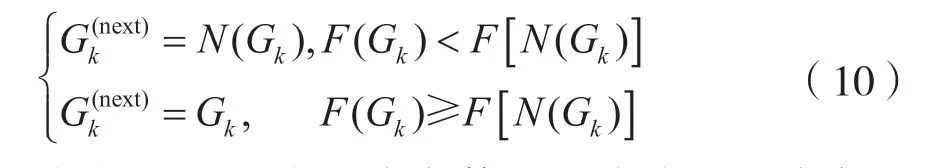
式中，F(Gk)表示染色体的适应度，固定每个染色体的局部优化次数，如50 次。

3.1.2 参数自适应

为了同时保证算法在训练时前期的多样性和后期的集中性，本文对交叉概率Pc和变异概率Vc做自适应性的调整：

式中，ρ1和ρ2分别是小于1 的常数，i表示迭代次数。

3.2 模型约束

优化模型含有大量的约束条件，且多数为较强的约束，如对图的边的数目的限制为常数。此类约束将使得多数染色体不符合条件而被淘汰，在前期的迭代中导致子代染色体数目过少甚至为0。因此，本文使用修复不可行解和惩罚函数法对问题约束条件进行处理，具体如下。

3.2.1 网络图的无向简单图约束

在种群初始化、交叉、变异和局部优化中，均可能造成图的邻接矩阵不满足无向简单图约束，如aij≠aji。因此，本文在每次涉及到改变图结构的操作后，对邻接矩阵进行逐行扫描修复。

3.2.2 网络图的边数目约束

由于几乎任何操作都将会改变图的边的数目，因此本文选择对图进行不可行解的修复。具体的修复方式如下。

假设边的数目为：

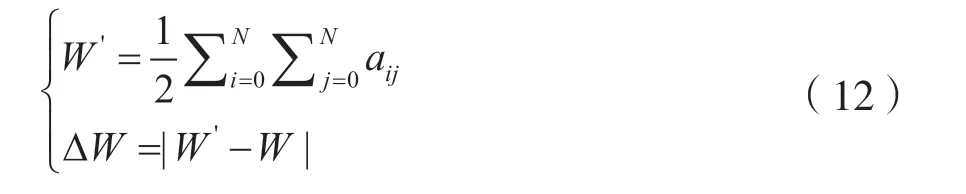
若W´-W>0，则随机选择邻接矩阵中的∆W个元素{a1,a2,…,a∆W}。集合中的每一个元素值都为1，且在原邻接矩阵中的下标均满足j≥i。将集合中的元素的值变为0，而后做满足式（1）中的无向简单图修复操作。反之，若W´-W<0，做相反操作。

3.2.3 图的连通性约束

对于图的连通性的修复较为困难，另外经过实验发现随机生成的图是连通图的概率在95＆以上，意味着只有较少数的图不是连通图。因此，在训练过程中，如果解不满足连通性约束，则放弃此解。即使用惩罚函数法，对不满足约束的解，其适应度值设为负无穷。

4 仿真实验及分析

4.1 优化拓扑结构的实验仿真

为了验证提出的网络拓扑优化算法的有效性，在仿真运行环境为64 位Windows10 操作系统、Python3.8、处理器为Intel i7 9570H、主频2.6 GHz、内存16 GB 的情况下进行实验，参数设置如表5 所示。首先，构造初始通信网得到其邻接矩阵。其次，通过表1 设置的参数进行遗传算法的初始化。最后，根据第4 节遗传算法的步骤得到自然连通度的最 优值。

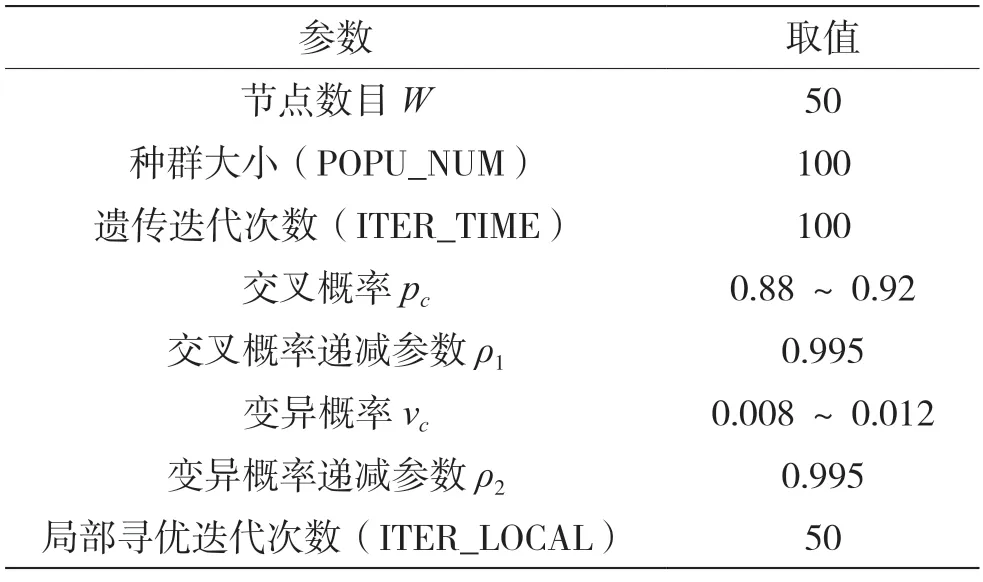
表5 参数设置

4.2 网络拓扑结构分析

仿真过程中，选用ER 随机图为研究对象。基本参数中，定义节点数N=50，边连接概率p=0.12。生成的ER 网络（连通图）拓扑结构与度分布，如图3 所示。

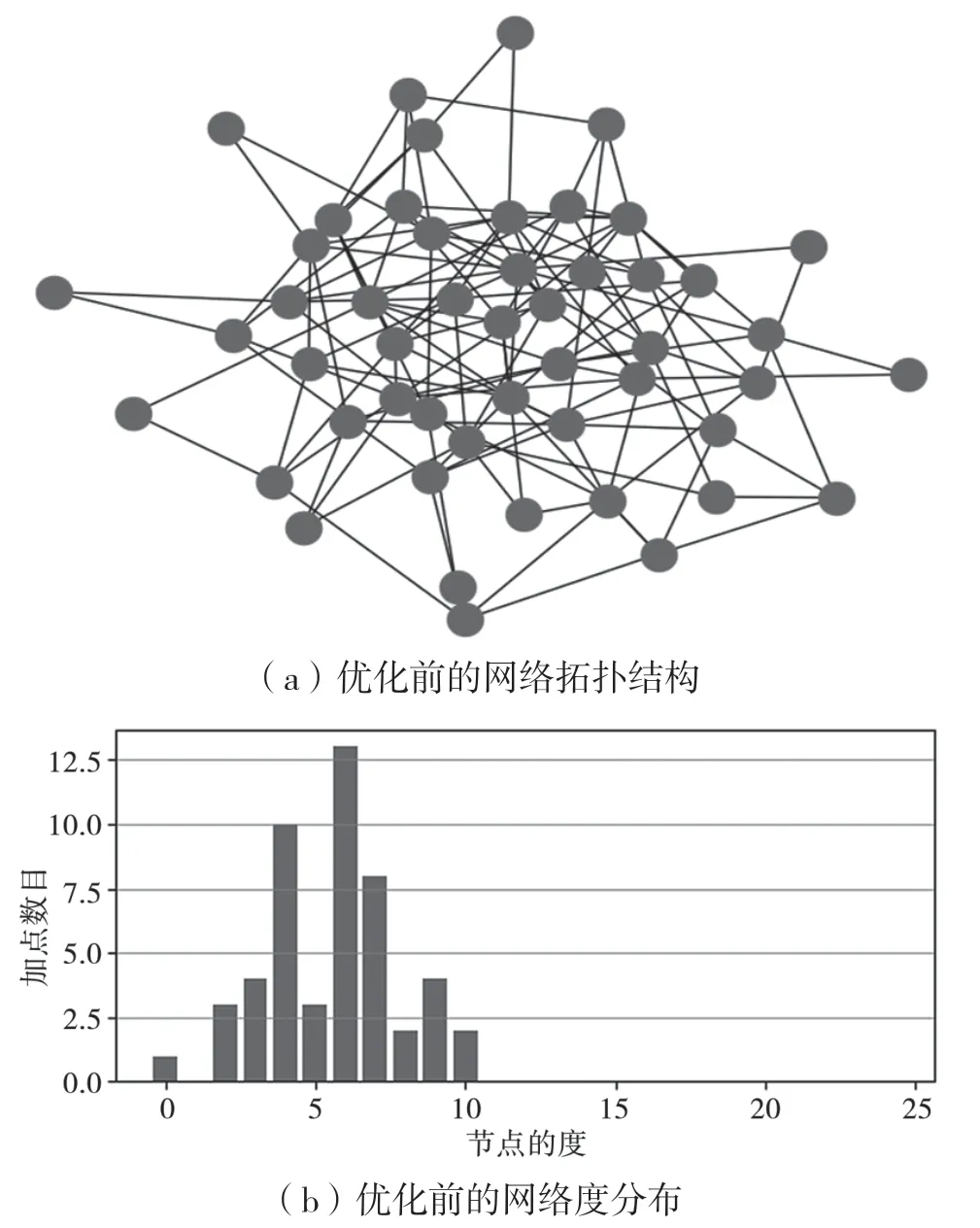
图3 网络拓扑结构与度分布

在保持网络节点数和链路数不变的情况下，优化前后的通信网拓扑结构及度分布分别如图3 和 图4 所示。随着迭代次数的增加，自然连通度值都明显呈上升趋势，如图5 所示。因此，遗传算法可用于求解通信网拓扑优化模型，且运用了算法收敛速度快等优点。

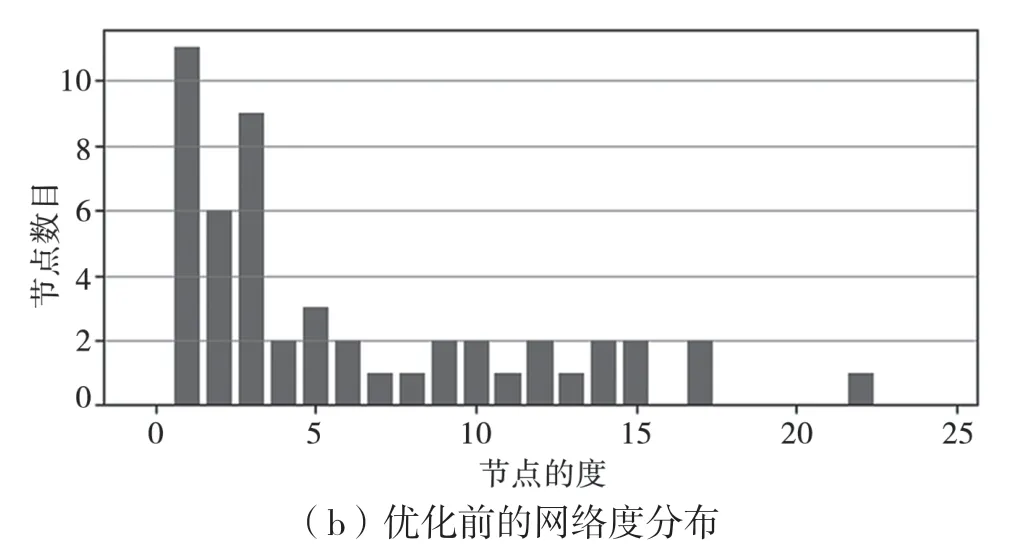
图4 网络拓扑结构与度分布

由仿真结果分析可得到以下基本结论。

（1）仿真分析验证了通信网拓扑结构优化模型的有效性和采用遗传算法求解该模型的可行性。由图5 可得，随着迭代次数的增加，自然连通度值呈上升趋势，最优结果在第100 次迭代达到7.6，说明网络拓扑结构可靠性得到增强。

（2）经遗传算法优化后，改变了通信网的度分布，其中网络节点倾向于与度大节点相连，度小节点数增加，而度大节点数减少。

（3）根据图3（b）和图4（b）可知，优化前网络度分布基本呈二项分布特点，而优化后网络中度值大的节点数增加，度由低到高节点数依次减少。因此，ER 网络拓扑结构优化后，度小的节点倾向于和度大节点相连。

（4）根据图5 可知，使用截断式选择法的遗传算法适应度函数值随迭代次数不断增大，优化效果明显高于以轮盘赌法和排序分组法为选择操作的遗传算法。

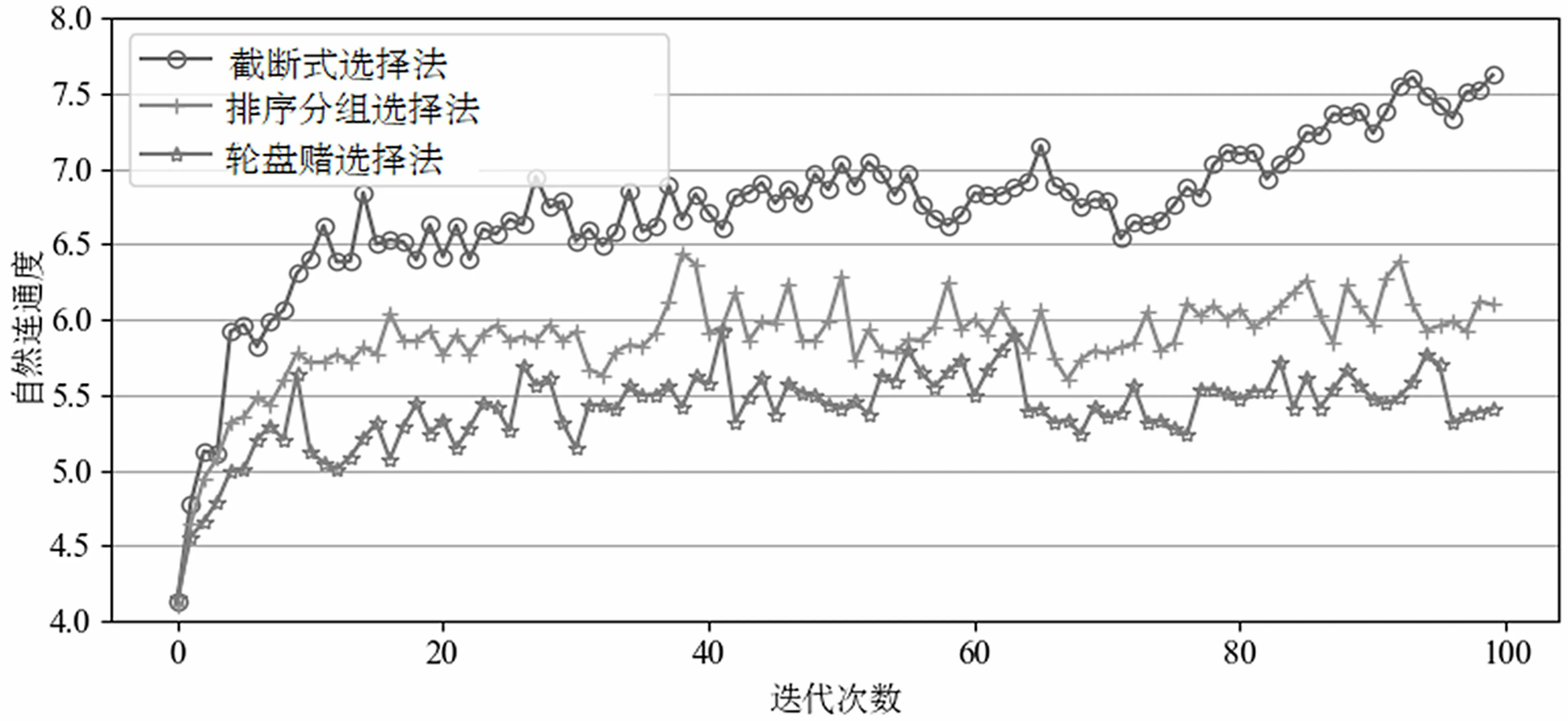
图5 自然连通度的迭代优化

4.3 可靠性分析

上述分析以自然连通度为网络可靠性测度建立拓扑优化模型，并采用遗传进化算法求解，提高了网络可靠性。本文采取随机攻击和蓄意攻击两种策略，分别对优化前后的通信网实施攻击并分析网络可靠性。通过仿真分析可知，通信网拓扑优化前后面临不同攻击策略具有以下特点。

（1）在随机去点攻击策略中（如图6（a）所示），优化后的网络可靠性在受到攻击时相比于优化前更加不稳定，若增大网络规模，将呈现更高的抗毁性。

图6 随机去除网络的节点与边

（2）在蓄意去点攻击策略中（如图7（a）和图7（b）所示），由于攻击方式是依次去除度大节点，优化后的网络在遭受此攻击时受损性更高。

（3）在按介数去边攻击策略中（如图7（b）所示），按边的介数大小依次去边。优化后网络面临该攻击方法表现出相对较强的可靠性，去除少量介数较大边，对网络可靠性影响有限。分析原因，在于优化后网络中度小的节点倾向于和度大节点相连，从而导致连接度大节点之间边的介数相对较大，因此边的冗余性较强。而针对优化前的网络结构，反之亦然。

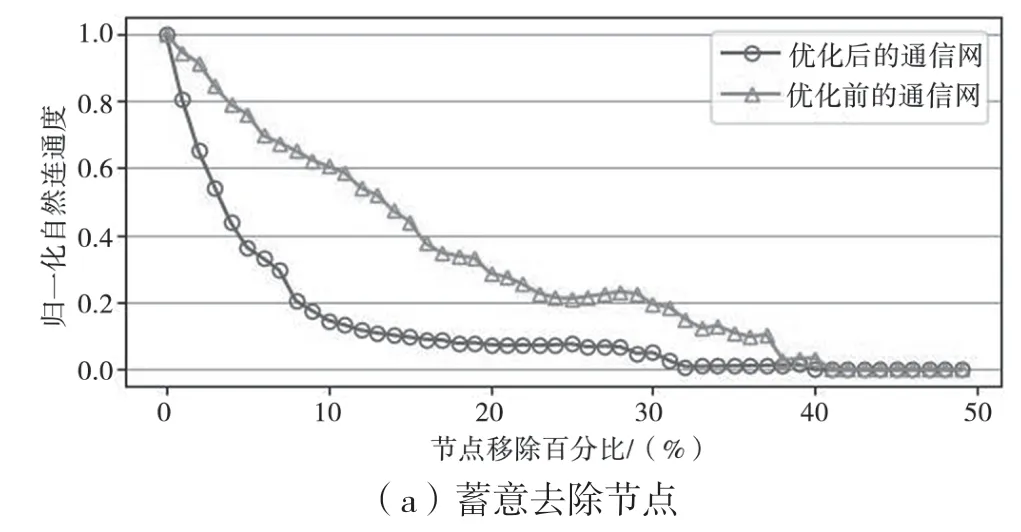
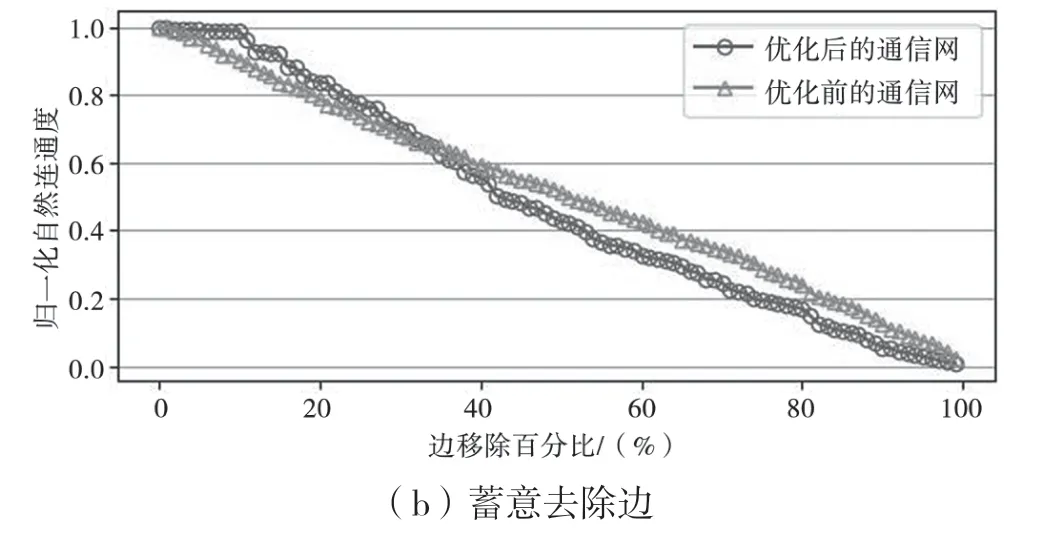
图7 蓄意去除边和节点

5 结语

本文首先建立了通信网拓扑结构优化模型，提出了基于遗传算法的求解方法，并通过仿真分析验证了模型与方法的可行性。

（1）建立以自然连通度为目标函数，以边的数量为约束条件的通信网可靠性组合优化模型；

（2）提出了基于遗传算法的通信网可靠性仿真优化算法，设计了变量编码，改进了选择操作，定义了交叉操作和变异操作，给出了算法流程；

（3）分析了优化前后网络拓扑结构与分布属性，表明优化后的通信网呈现出明显的同配度关联模式，度小节点倾向于与度大节点相连，高度数节点相对聚集，高度数节点之间连接较多，大多数节点之间连接较少，网络拓扑呈现出“核心-外围”结构。

通过可靠性分析发现，经遗传算法优化后的通信网在面对随机去点攻击和按介数去边攻击时表现出更高的抗毁能力，而面临蓄意去点攻击时则抗毁能力相对较差。因此，实际应用中应结合攻击策略适应性的构建初始通信网拓扑结构。