基于改进因子分析法的影响苏州现代服务业集聚区发展的因素分析

程毛林，韩 云

（1.苏州科技大学 数学科学学院，江苏 苏州 215009；2.苏州科技大学 商学院，江苏 苏州 215009）

产业集聚区是指政府统一规划、企业相对比较集中、实现资源集约利用、提高整体效益的区域。苏州市从2007 年开始打造和培育现代服务业集聚区，经过10 年的发展，服务业集聚区对全市服务业集聚、集约发展起到了很好的促进和推动作用。近年来，现代服务业的跨越发展，服务业集聚区的形态、产业发展重点、规模体量、运作模式等有了较大变化，形成了一批形态新、成长性好、发展进度快、示范引领强的新的服务业集聚区，同时，也有部分市级现代服务业集聚区发展缓慢，已不能适应服务业集聚区提档升级发展要求。分析和掌握影响苏州现代服务业集聚区发展的主要因素，对制定区域发展计划和决策非常重要[1-4]。影响苏州现代服务业集聚区发展的因素很多[5-7]，主要包括四大方面，即集聚区之间的关系、发展潜力、发展风险、集聚区的服务产业链。每个方面均包含相关指标[8]。

因子分析法是分析此类问题的重要方法[9-12]。一般而言，在有多个指标的许多问题中，用因子分析法可以寻找出支配多个指标的少数几个公因子或共性因子。这些公因子是彼此独立或不相关的，在所研究的问题中，可以不损失或很少损失原指标所包含的信息，以公因子（新变量）代替原指标（原变量）作为研究对象。用得到的少数几个公因子进行因素分析。

有许多研究者利用因子分析法做了各种研究。李燕华和路立敏[13]采用因子分析法对23 家沪深A 股的水泥行业上市公司进行2019 年财务绩效综合评分，结果显示，水泥上市公司之间财务绩效表现差距较大，行业整体水平有待提升。陈媛媛[14]突破传统的研究方法与研究视角，利用解释结构理论及模型来进行高校辅导员职业能力的因子分析，构建高校辅导员职业能力因子的多级递阶解释结构模型，探讨职业能力因子之间的内在关系，为高校辅导员职业化建设提供相关建议。陈新铄等人[15]以南京市为例，分析了南京市大气污染影响因素，研究了南京市大气污染治理中存在的问题并提出改进措施，为南京市及全国其他城市大气污染治理提供参考。宋玉康等人[16]选取苏州10 个典型社区作为研究对象，利用因子分析法深入剖析影响城郊集中社区公共空间满意度的关键因子。结果显示：可达性、采光性、健身设施完善度、设施管理维护等8 个因子是影响公共空间满意度的重要客观因子；居民年龄、月收入、入住时间与公共空间满意度呈现显著相关性，是影响满意度的3 个主观因子。张秀伟[17]运用因子分析模型中不同的参数估计方法，客观、有效地确定新课程课堂教学评价的基本因素，较好地为新课程课堂教学评价的实施提供依据。

为了得到相关指标的数据笔者对178 家苏州工业园区现代服务业集聚区的企业进行了问卷调查。由于调查的数据比较分散，一般的因子分析法效果不太理想，表现为寻找的少数几个公因子其累计贡献率不高，为此文中选用优化方法对原始数据进行Box-Cox 变换[18－22]使这寻找的少数几个公因子其累计贡献率最大，此法称为改进因子分析法。

1 改进因子分析法

对比较分散的数据，传统的因子分析法在一些情况下得到的少数几个公因子其累计贡献率不高，而且一般只能处理线性问题。因此，文中提出了一种基于非线性变换的因子分析法，该方法通过Box-Cox 变换，选择Box-Cox 变换参数，使变换后的变量进行因子分析得到的少数几个公因子其累计贡献率有最大值，这种改进因子分析法效果显著。

1.1 Box-Cox 变换

Box-Cox 变换是常用的数据变换方法，即

其中，yi为第i 个变量（指标）的原始观测值，xi是第i 个变量变换后的数值，λi为待确定的参数。

广义Box-Cox 变换，即

其中，λ1i、λ2i为2 个待确定的参数，要求yi+λ2i＞0。此广义Box-Cox 变换是一般Box-Cox 变换的推广。对yi为负数值的情况下可使用下式变换

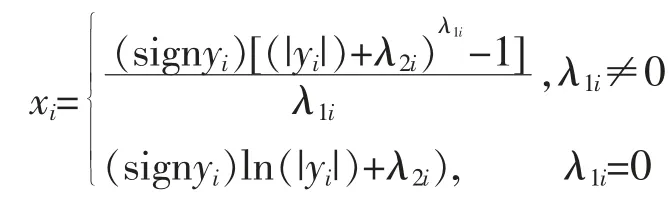
其中，sign 为符号函数，λ1i、λ2i为2 个待确定的参数。

1.2 因子分析法

由于文中调查的数据量化后均为正数，所以实行一般的Box-Cox 变换。使用优化方法，选择Box-Cox 变换参数，使变换后的变量进行因子分析得到的少数几个公因子其累计贡献率有最大值。

具体步骤如下：

（1）设变换后的变量为x1，x2，…，xm

现有n 个样品，相应的观测值为xik，i=1，2，…，n；k=1，2，…，m。作标准化变换后，将xk变换成xk*，即

（2）求矩阵R 的特征值和特征向量

设相关矩阵为R＝X·X′（假定标准化后的矩阵仍记为X），标准特征方程|R-γI|=0，利用一定的数学方法，求出相关矩阵R 的特征向量矩阵A 和特征值γ1＞γ2＞…＞γp≥0，并使F=A′x，其中F 为主因子阵。

（3）建立因子模型

在因子分析中，一般将A，F 分解为两部分：

则因子模型为

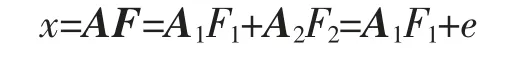
A1称为因子载荷矩阵，F1称为主因子，e 称为特殊因子。因子模型可具体写成

式中，f1，f2，…，fm为主要因子，分别反映某一方面信息的不可观测的潜在变量；aij为因子载荷系数，是第i 个指标在第j 个因子上的负荷，若某指标在某因子中作用大，则该因子的载荷系数就大，反之亦然；ei为特殊因子，实际建模中可忽略。

（4）确定因子贡献率及累计贡献率

（5）因子载荷阵的变换

由因子模型阵得到的初始因子载荷阵，如果因子负荷的大小相差不大，对因子的解释可能有困难。因此，为得出较明确的分析结果，通过旋转坐标轴，使每个因子负荷在新的坐标系中能按列向0 或1 两极分化，同时也包含按行向两极分化。旋转的方法有正交旋转和斜交旋转两种，由于选择的旋转方法不同，结果也就不同，一般以能得到较明确的分析结果为最终计算结果。

2 影响苏州现代服务业集聚区发展的因子分析

2.1 影响苏州现代服务业集聚区发展的指标体系构建

从系统角度全面考虑，笔者将影响苏州现代服务业集聚区发展的指标划分为三个层次，自上而下分别为目标层（1 级指标）、控制层（2 级指标）、指标层（3 级指标）。每类指标分别确定若干个子指标。根据指标设计的综合性、层次性、代表性、实用性、动态性原则，考虑苏州工业园现代服务业集聚区企业的实际情况，课题组设计了下列指标，指标体系见表1。

表1 影响苏州现代服务业集聚区发展的指标体系

2.2 数据建模与分析

对178 家苏州工业园区现代服务业集聚区的企业进行了问卷调查，指标从高到低，从大到小分为5 级，分别为A、B、C、D、E。首先，对原始资料量化，A 为100，B 为80，C 为60，D 为40，E 为20，将上述经过整理的指标数据利用MATLAB2106A 软件进行因子分析。

对15 个三级指标（变量）的数据进行Box-Cox 变换

文中用优化方法让前6 个主要因子贡献率之和最大，优化模型如下

得到15 个变量的Box-Cox 变换参数λi，参数取值结果见表2。得到变换后的因子分析结果（6 个因子特征值、方差贡献率和累计贡献率）见表3。

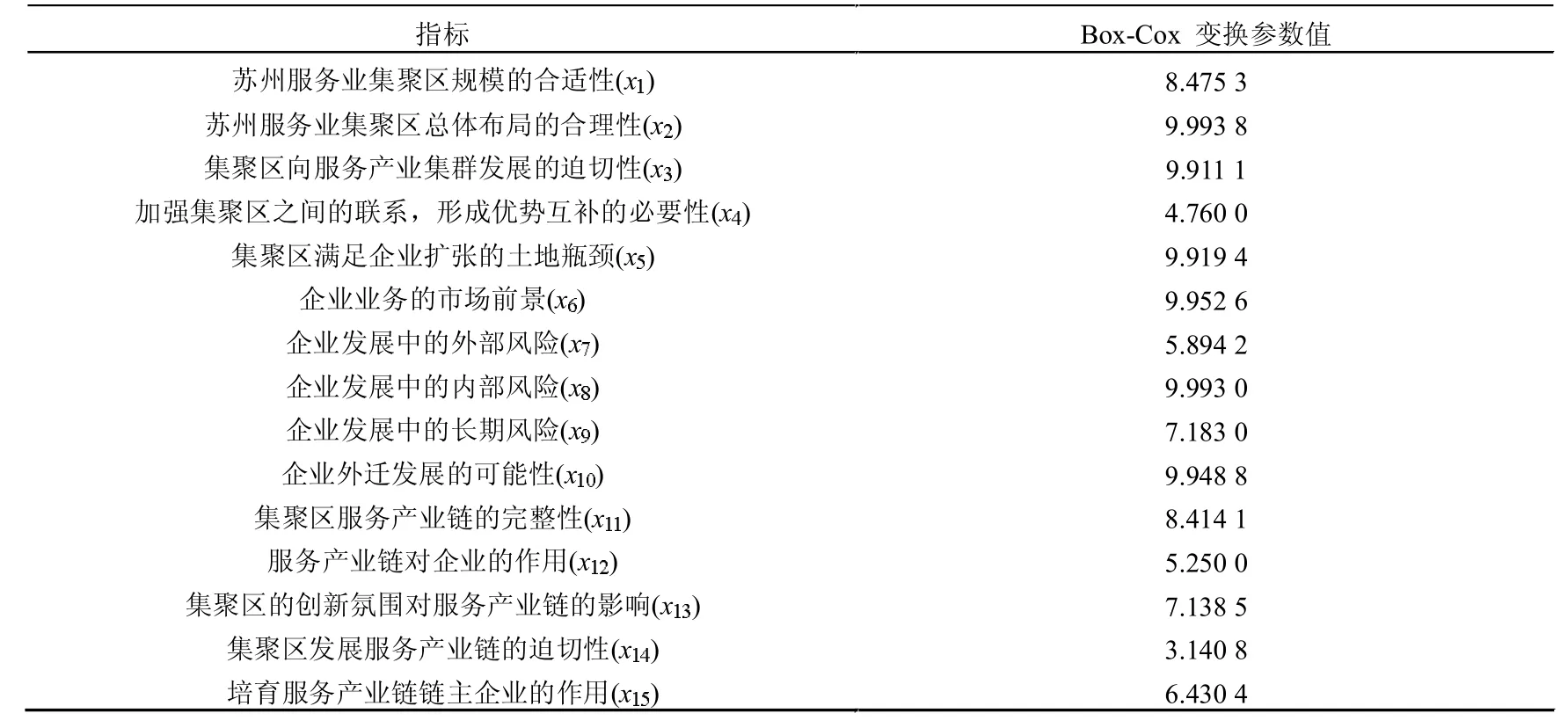
表2 Box-Cox 变换参数结果

表3 特征值、方差贡献率与累计贡献率

从表3 中可以看出，变换前第一因子的方差占所有因子方差的13.38%，前6 个因子的方差贡献率累计48.08%，变换后第一因子的方差占所有因子方差的18.76%，前6 个因子的方差贡献率累计70.01%，基本上能够描述和解释影响苏州现代服务业集聚区发展的情况。

由于初始的因子载荷矩阵中各因子含义的描述不太明晰，文中对初始因子载荷矩阵进行方差最大旋转，旋转后的载荷矩阵见表4。

表4 旋转后因子载荷矩阵

从表4 中可以看出，第一公因子在集聚区服务产业链的完整性、企业业务的市场前景、服务产业链对企业的作用、集聚区的创新氛围对服务产业链的影响上具有较大的载荷，可以反映服务产业链的影响，将其定义为服务产业链因子；第二公因子在企业外迁发展的可能性上有较大的载荷，将其定义为企业外迁发展因子；第三公因子在加强集聚区之间的联系，形成优势互补的必要性上有较大的载荷，可以反映集聚区企业之间的联系和优势互补强弱，将其定义为优势互补因子；第四公因子在苏州服务业集聚区总体布局的合理性上有较大的载荷，可以反映集聚区总体布局的状况，将其定义为总体布局因子；第五公因子在培育服务产业链链主企业上有较大的载荷，可以反映培育服务产业链链主企业方面的情况，将其定义为培育链主企业因子；第六公因子在集聚区满足企业扩张的土地瓶颈上具有较大的载荷，将其定义为土地瓶颈因子。这六大因子分别反映的相关指标（载荷大）是影响苏州现代服务业集聚区发展的主要因素，且影响大小从第一公因子反映的指标到第六因子反映的指标依次降低。

3 结语

对178 家苏州工业园区现代服务业集聚区的企业进行了问卷调查，用因子分析法进行因素分析，得到影响苏州现代服务业集聚区发展的主要因素。由于调查的数据比较分散，一般的因子分析法处理效果不太理想，表现为寻找的少数几个公因子其累计贡献率不高，为此文中选择优化方法对原始数据进行Box-Cox 变换使这寻找的少数几个公因子其累计贡献率最大。实证分析表明，改进的因子分析法使得前面几个公因子累计贡献率显著提高，且能反映原始指标包含的信息。