求解非光滑问题的修正HS共轭梯度法

胡亚萍，王玉杰，刘丽英

(天津科技大学理学院，天津 300457)

考虑无约束优化问题min{ f(x) |x ∈ℝn}，其中f: ℝn→ℝ为非光滑凸函数．非光滑问题中的目标函数是连续不可微函数，传统的优化算法不能直接用于求解该问题．与非光滑凸优化问题紧密相关的是目标函数Moreau-Yosida正则化[1]，正则化函数F(x)是定义在整个空间nℝ上的可微的凸函数，并且与原非光滑优化问题拥有相同的解集合．求解非光滑优化问题的常用算法有Bundle法和信赖域法[2-4]．近年来，Yuan等[5-6]和Hu[7-8]提出的梯度类算法在求解非光滑问题时表现较好．其中文献[6]基于BFGS修正技术提出的修正PRP共轭梯度法需要较大的存储空间和计算量，它每步迭代时的计算量和内存需求均大于共轭梯度类算法．本文结合Moreau-Yosida正则化和非单调线搜索技术，提出了修正的HS共轭梯度算法求解非光滑优化问题．新算法具有满足共轭性条件、自动具有充分下降性、给出近似参数选取方式、克服存储需求大与算法复杂等特点．数值结果表明，与文献[6]的算法相比，新算法具有收敛速度快、精度高的优点．

1 算 法

记p(x) =argmin {θ(z ) |z ∈ℝn}，且定义θ(z)=f(z)+ ‖z -x‖2/(2λ)，由于θ(z)是一个强凸函数，极小值点p(x)存在且唯一．于是非光滑凸函数f(x)的Moreau-Yosida正则函数F(x)表示为

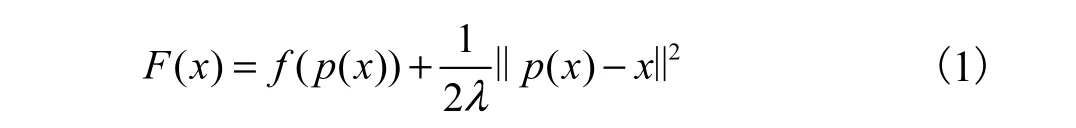
正则化函数F(x)是连续可微的凸函数，但同时注意到F(x)未必二次可微．F(x)在点x处的梯度为g(x) =∇F (x) = ( x - p(x) )/λ．然而θ(z)的极小值点p(x)一般很难甚至不可能精确求解，这便不能直接利用p(x)的精确值来确定函数值F(x)和梯度值g(x)．但是对任意 x∈ℝn和任意的近似参数ε＞0，存在近似值 pα(x,ε) ∈ℝn满足

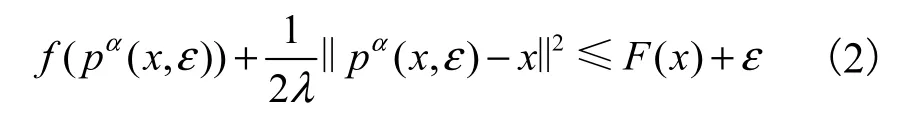
于是，可以利用pα( x,ε)来确定F(x)和g(x)的近似值，即

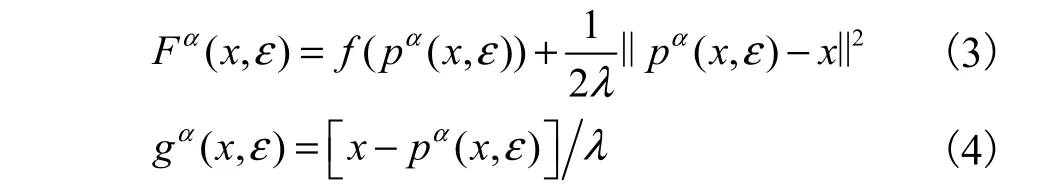
一些用于求解近似极小值点pα( x,ε)的算法见文献[9]，近似值Fα( x,ε)和gα( x,ε)满足下面的性质[9]：

本文提出修正HS共轭梯度算法，简记为MHS算法，令

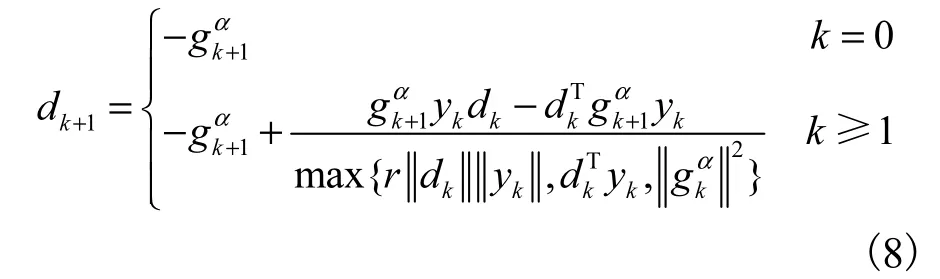
算法MHS的步骤如下：

步骤0：令k=0，给定初始点 x0∈ℝn，s＞0，ξ∈ (0,1)，σ∈ (0,1)，λ＞0，ρ＞0，E0=1，一个严格下降的正序列{τk}满足τ0≤1且，ε0=τ0，J0= Fa(x0,ε0)，d0=- gα(x0,ε0)．

步骤2：选取εk1+满足

由非单调Armijo-型线搜索确定步长 kα：

其中，αk=s 2-ik，ik∈{ 1,2,…}．

步骤3：令 xk+1= xk+αkdk．若则算法停止．

步骤4：由下面公式更新Jk1+

步骤5：由式(8)计算搜索方向dk1+．

步骤6：令k=k+1，转步骤1．

2 全局收敛性

本节讨论修正HS共轭梯度算法用于求解非光滑凸优化问题时的收敛性．为此，需要文献[5-7]中的假设条件．

假设A．序列{Vk}有界，即存在常数M ＞0使得

其中矩阵 Vk∈∂Bg (xk)．

假设 B．正则化函数F有下界．

引理1由式(8)的定义，搜索方向满足性质

证明:当k=0时，d0=- gα(x0,ε0)，式(11)、式(12)显然成立．

当k≥1时

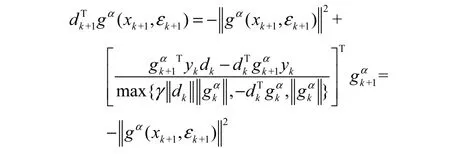
故(12)成立．

故(13)成立．证毕．

根据假设B和修正HS算法中的步骤5，提出下面的引理．引理表明该搜索是适定的，证明方法与文献[10]中的引理1类似，故省略．

引理2若假设B成立．序列{xk}由算法MHS产生，则 Fa(xk,εk)≤ Jk≤ Ck对每一个k成立，其中另外，存在kα满足线搜索中Armijo条件．

由假设A，类似于文献[5]中的引理4.2，可以得到下面的引理．

引理3若假设A成立．序列{(xk,εk)}由算法MHS产生．假设成立．则存在常数m0＞ 0，满足αk≥ m0．

定理1若假设A，假设B和引理3的条件成立，序列{xk}由算法MHS产生，则有，且序列{xk}的每一个聚点都是非光滑凸优化问题(1)的最优解．

证明：先用反证法证明假设存在常数є0＞0和k0＞0使得‖ gα(xk,εk‖)≥є0对所有的 k＞k0成立．由式(5)和假设B，知 Fa(xk,εk)有下界．结合引理2，得到Jk有下界，且

另一方面，由式(9)和引理3，有

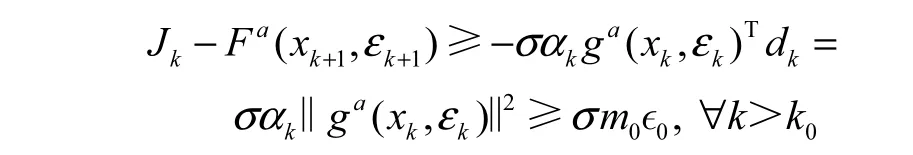
因此，上式结合式(10)可推出

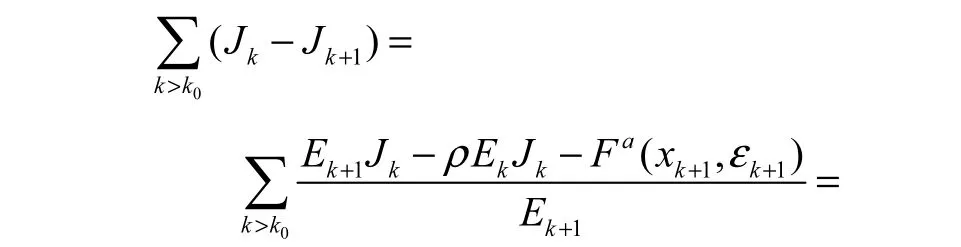
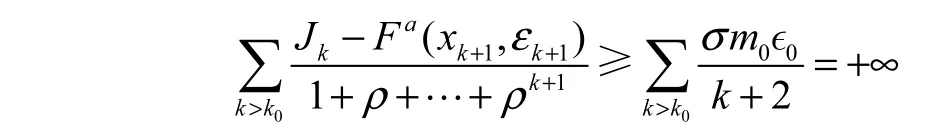
由{εk}的定义和式(7)，有．令 x*是序列{xk}的一个聚点，不妨设存在一个子列{xk}K，使得

由正则化函数F(x)的定义，有

式中令k→∞，有 x*=p(x*)成立．因此x*是非光滑优化问题(1)的最优解．证毕．

3 数值实验

算法MHS、MPRP[6]和BT[11]的数值结果见表1.非光滑测试函数信息可参考文献[5]的表1．在实验中，取参数s=λ=1，ρ=0.75，σ=0.9，εk= 1/( k +1)2，终止准则为‖ ga(x,ε)‖ ≤ 10-5．表1中f(x)表示算法终止时的函数值；fops(x)表示目标函数的最优值．

从表1中迭代次数、函数值计算次数和算法终止时的函数值三方面综合来看，修正HS共轭梯度算法对求解非光滑问题是有效的．

表1 不同算法的数值结果 Tab. 1 Numerical results of different algorithms

4 结 语

非光滑优化问题是最优化理论与方法的重要分支，其求解也是优化领域的难题之一．本文结合Moreau-Yosida正则化和非单调线搜索技术提出了非线性修正HS共轭梯度算法用于求解非光滑优化问题．在适当条件下，证明了该算法具有全局收敛性．数值结果表明新算法在求解非光滑优化问题方面是有效的．