面向物流场景的关键设备与输送线混合布局方法
朱俊杰,李 琳,2*,曹 力,2,刘晓平,2
(1.合肥工业大学计算机与信息学院,安徽 合肥 230601;2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230009)
设备布局问题是工业生产领域的一个重点研究问题,主要研究对于给定的一组工业生产设备,在已知设备间的物流量和物流关系等数据的情况下,确定设备在生产车间内的精确布局,从而实现生产成本、设备占地面积等目标的最优化.设备布局对于工业生产意义重大,Tompkins等[1]的研究指出,良好的设备布局可以减少工业生产中10%~30%的成本.物流场景的布局问题从广义上属于设备布局问题的一种,但其也有自身的特点:对于物流场景,其主要功能是对物料进行分拣、运输和存储,物流场景中主要有关键设备和输送设备两类设备,前者指各种加工、分拣和存储设备,后者则用于连接不同的关键设备,以实现物料在关键设备间的运输.为便于表述,下文以设备代指关键设备,以输送线代指输送设备.
为了解决面向物流场景的布局问题,可从传统设备布局问题开始研究.设备布局问题已被证明是一个非确定性多项式困难(NP-hard)问题,其解空间十分庞大,同时对于多目标设备布局问题来说,在求解多个目标时可能存在冲突,以上两个原因导致设备布局问题难以求出精确的全局最优解.元启发式算法能在可接受的时间空间代价下求出该问题的可行解,对于解决这类问题有着很好的效果.目前在设备布局领域有大量关于元启发式优化算法的研究,包括遗传算法[2-6]、粒子群算法[7-9]、模拟退火算法[10-14]、人工免疫算法[15-16]、差分进化算法[17]、禁忌搜索算法[18]、教与学算法[19]等,学者们结合具体的布局问题,或加入新的搜索策略[2-5,9,11],或加入新的约束处理策略[8],或建立全新的布局模型[6-7,10],或将多种优化算法融合[20],以提高布局算法的时间效率和最终布局效果.
针对设备布局问题,目前已有大量成熟的布局方法,但针对面向物流场景的混合布局问题,传统的设备布局方法还存在一些缺陷.主要表现为:1) 由于输送线同时具备设备属性和路线属性,其中设备属性是指输送线本身也是设备,和其他设备一样需要满足重叠等约束,路线属性是指其用于连接不同的关键设备,可将其看成线路,每条输送线的长度和走向要在确定设备位置并进行布线后方可确定,因此传统的设备布局方法并不适用于输送线.2) 传统的设备布局方法由于没有考虑输送线布局,一般均采用理想的曼哈顿距离来表示设备间的距离,但这并不符合实际.如图1所示,按照曼哈顿距离计算的输送路径会导致设备与输送线发生冲突,同时这样也未考虑两者之间的布局约束、设备与输送线的连接位置等因素.3) 目前很多文献[4-5,13-19]将设备按照行和列进行布局,设备位置不能连续变化,而本文中的设备和输送线位置均可连续变化,这样更符合实际,同时也导致约束处理过程更复杂,需要提出全新的约束处理策略.
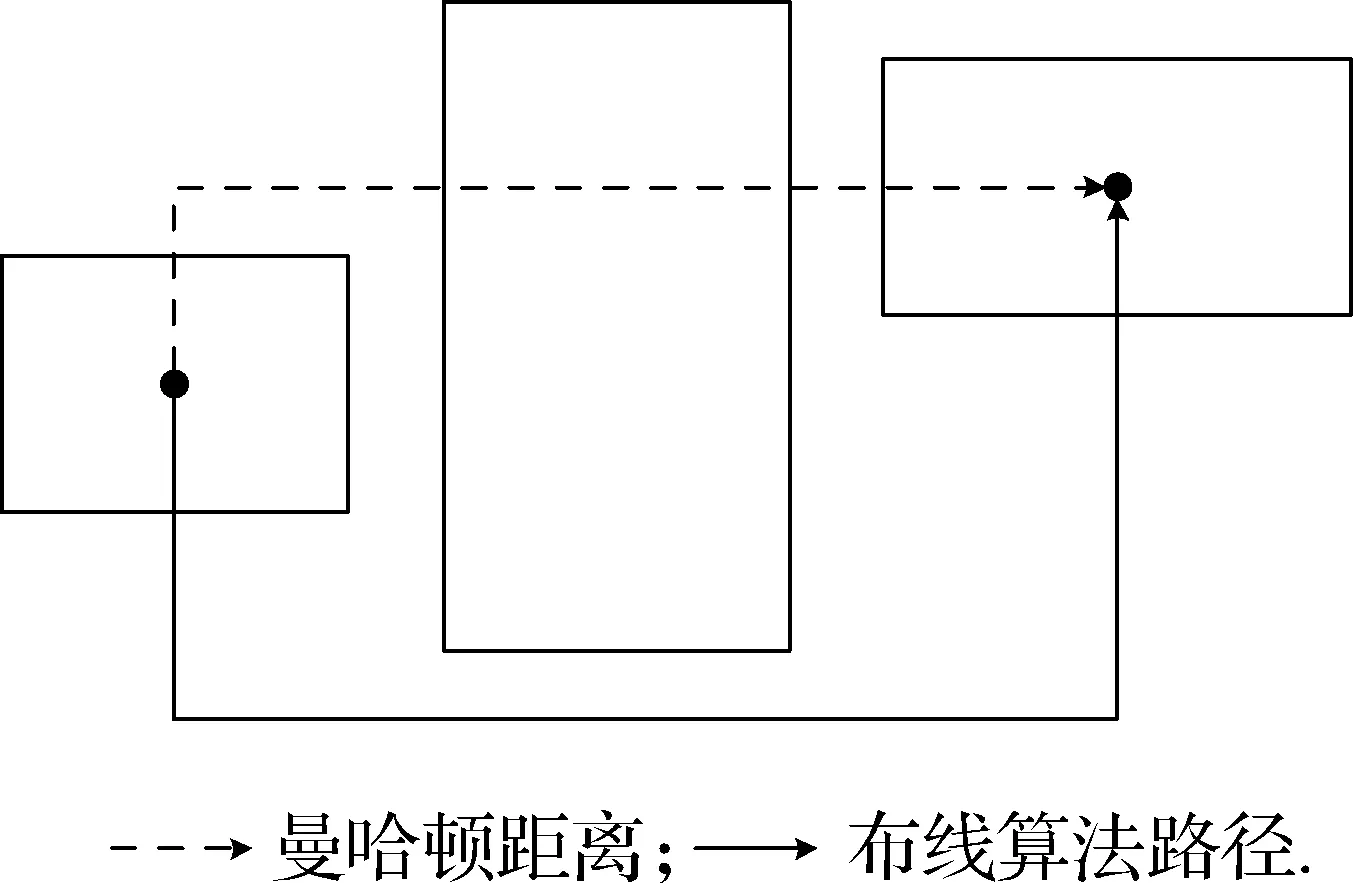
图1 两种不同的最短距离Fig.1 Two different kinds of shortest distance
为此,本文首先建立一个考虑物料搬运总成本和输送线总成本的多目标优化数学模型,然后使用混合方法进行布局.混合布局方法分为两部分:第一部分为多目标元启发式布局算法,用于实现设备布局、解的更新与迭代,该部分可以选择不同的元启发式算法,目前在设备布局领域,研究较多的为多目标遗传算法和多目标粒子群算法(MOPSO),模拟退火算法则一般用于解决单目标设备布局问题[10,12-14],或者使用加权的方法将多目标问题归一化为单目标问题再求解[11].因此,为了验证本文方法的有效性和适用性,本文分别选择MOPSO和非支配排序遗传算法2(NSGA2)[21]这两种较为通用的多目标元启发式算法.第二部分为布线算法,用于实现输送线布局,本文没有使用理想的曼哈顿距离表示设备间路径,而是使用一种基于多目标评估的路径搜索算法实现输送线的布置,并结合实际问题,对该布线算法中的路径点矩阵构造策略和路径点选择评估函数等进行了修改.此外在方法中加入了处理关键设备和输送线约束的策略.最后通过同基于MOPSO和NSGA2的传统设备布局方法对比,验证本文方法对于解决物流场景中关键设备和输送线混合布局问题的有效性.
1 问题描述和数学建模
1.1 问题描述
本文在已知物流设备的种类与数目,以及物料种类、物料量、运转路线等条件下,实现对设备与输送线的自动化布局,从而实现物料搬运总成本和输送线总成本最小的目标.
结合相关物流背景知识和实际情况,列出本文问题的假设条件:
1) 车间大小固定且足够容纳所有设备和输送线;
2) 所有设备大小固定,且均视为矩形,若不是矩形,则用一个包络矩形近似表示设备形状,如图2(a)所示;
3) 设备的朝向分为上下左右4种,默认方向为向上,规定y轴正方向为设备上方;
4) 每个设备的加工效率和出入口位置已知;

6) 设备与设备之间,以及设备与输送线间有最短距离限制;
7) 输送线分为用于物料的长距离直线运输(如直线输送机)和用于实现物料转向的输送机(如万向轮和转弯输送机);
8) 输送线有最短的长度限制.这里的长度指的是一条输送线上两个相邻转弯点间的长度,因输送线也需考虑尺寸,故要求两个转弯点间的路线长度不小于一个转向输送机的长度,否则会导致设备发生如图2(c)所示的重叠,违反了物理约束;

图2 物流设备布局的问题举例Fig.2 Problem examples of logistics equipent layout
9) 所有输送线的输送速度相同;
10) 输送线只允许向水平或垂直方向延伸,不允许出现斜向的输送线;
11) 物料的种类、数量和经过的设备路线已知.
1.2 数学建模
1.2.1 布局坐标系
设备布局在二维平面中进行.如图3所示,建立了一个二维坐标系统,用于表示车间的坐标范围、设备位置和输送线路信息.其中,O点为坐标系原点,x轴为车间的长度所在边,y轴为车间的宽度所在边,点的几何位置用二维坐标表示,Ein和Eout分别表示车间入口和出口.设备所在包络矩形的中心坐标表示其布局位置,输送线路则使用路线起始点、终点以及各转弯点间的连线表示.

图3 布局坐标系Fig.3 Layout coordinate system
1.2.2 目标函数
目标1为物料搬运总成本f1(x)最小,f1(x)如式(1)所示.由于单个车间内可能有多种物料需要进行加工、运输和存储,所以设置物料种类数目为K,Sk表示物料k的总量,Lk表示物料k经过的输送线总长度.对于物料k,其经过的设备及所在设备出入口的序列构成了在车间中的运输路线,序列的总长度即为Lk.
(1)
目标2为输送线总成本f2(x)最小,f2(x)如式(2)所示.这里将输送线成本分为直线输送机和转弯输送机两部分计算,其中LS表示直线输送机的总长度,CS表示单位长度直线输送机的成本,ST表示转弯输送机的总数,CT表示单个转弯输送机的成本,LS和ST在输送线布局完成后得到,CS和CT为已知量.本文中,允许两条输送线中间有公用部分,在计算成本时公用部分仅计算一次.
f2(x)=LS×CS+ST×CT.
(2)
1.2.3 约束条件
布局时,设备与输送线要满足一系列约束条件:
1) 根据设备要位于车间内,有如式(3)~(6)所示的约束条件.
Xi-0.5li≥0,∀i∈{1,2,…,I},
(3)
Yi-0.5wi≥0,∀i∈{1,2,…,I},
(4)
Xi+0.5li≤L,∀i∈{1,2,…,I},
(5)
Yi+0.5wi≤W,∀i∈{1,2,…,I}.
(6)
其中,I表示设备总数,Xi和Yi分别表示设备i的x轴和y轴坐标,li表示设备i的长度,wi表示设备i的宽度,L表示车间长度,W表示车间宽度.
2) 设备之间不能重叠,但有最小距离限制.本文同时处理这两个约束,通过给设备4个方向各设置一个禁区距离,布局时只需实现设备外层范围间不重叠,就同时实现了设备重叠和距离约束.如式(7)所示,I(ai)表示设备i考虑禁区距离后的内部范围.
I(ai)∩I(aj)=∅,i≠j,∀i,j∈{1,2,…,I}.
(7)
3) 输送线布局约束.首先见1.1节中的8),输送线有最短长度约束,同时直线输送机设备本身也有一个最短长度,其长度不能小于这个最小值.综合这两个因素,加入输送线长度约束,Lmn表示两个转弯点m和n之间的输送线长度.WC表示输送机本身的宽度,LCM表示直线输送机的最短长度限制.转弯点间的长度约束如式(8)所示.
Lmn≥LCM+WC.
(8)
不同输送线之间也不能发生重叠,如式(9)所示,I(li)和I(lj)表示任意两条输送线的设备范围.
I(li)∩I(lj)=∅,i≠j.
(9)
1.2.4 布局结果
布局结果包含两部分:
1) 所有设备的坐标及朝向信息.表示为(X1,Y1,D1,X2,Y2,D2,…,Xi,Yi,Di,…,XI,YI,DI),其中Di表示设备i的朝向,有Di∈{Dup,Ddown,Dleft,Dright},即每个设备有上下左右4个朝向.

2 算法描述
本文的混合布局方法整体流程如下:首先输入物流场景布局参数,然后对设备位置信息进行编码,根据具体的元启发式优化方法产生初始解,并使用各自的启发式策略对解进行更新,结合输送线布局结果计算目标函数值,根据目标函数值对解进行选择和迭代,同时对关键设备和输送线布局的约束进行处理,通过不断迭代得到最终布局结果.
本文分别基于MOPSO和NSGA2,并结合基于A*算法改进的多目标评估路径搜索算法(具体改进见2.3节),实现了MOPSO-Route和NSGA2-Route两种混合布局算法.
算法的整体流程如图4所示,本文将MOPSO和NSGA2算法嵌入其中,具体地,对于不同的元启发式算法,不同的步骤主要是解的编码和初始化、解的更新、解的筛选与迭代,其他步骤是一样的.表1给出了它们对应具体算法的步骤.

图4 混合布局算法流程Fig.4 Hybrid layout algorithm flow

表1 MOPSO和NSGA2的不同步骤
2.1 解的编码和初始化
本文对关键设备的坐标和朝向信息进行编码:
XI,YI,DI],
(10)
为加快算法收敛速度,在初始化时本文采取一种策略来保证初始解的非重叠性和多样性,步骤如下:
1) 将车间按照长宽等距离分割为二维网格,分割步长设为1 m;
2) 检查待布局设备是否为空,若为空,结束;否则,从待布局设备中随机选择一个进行布局.具体地,从空闲区域开始,在1 m×1 m范围内随机产生一个设备位置与朝向信息;
3) 检查该设备位置与朝向是否与其他设备重叠,若不重叠则确定该设备的位置和朝向,并从待布局设备中删除该设备,然后进入步骤2);否则继续试探设备新位置.
2.2 解的更新与迭代
得到初始解后进入更新迭代过程.在每次迭代中,首先更新当前解以产生新解,然后根据设备和输送线布局结果计算新解的目标函数值,接着进行解的选择,更新相关参数并产生下一代解集.不同算法的具体更新迭代策略有所不同:
1) 遗传算法[2-6]通过父染色体之间的交叉、变异产生新个体,然后采用选择策略(轮盘赌、锦标赛选择等)结合目标函数值从父个体和新个体中选择最优个体组成子种群.
2) 粒子群算法[7-9]中,粒子通过跟踪两个极值更新自身,分别为个体最佳极值Pbest和全局最佳极值Gbest.粒子更新后即产生新一代粒子群,然后计算新一代粒子群的目标函数值,并以此更新Pbest和Gbest.
2.3 基于多目标评估的输送线布局算法
每次更新设备位置后进行输送线的布局.本文使用基于多目标评估的路径搜索算法实现不同设备之间的布线,并根据具体问题对其进行改进.下面介绍输送线布局算法过程:
1) 构造路径点矩阵用于寻路.一般采用等间隔划分二维网格的方式构造路径点矩阵,而在本文问题中,因设备位置可以连续变化,难以确定间隔的粒度,故本文选择利用设备布局的信息,通过提取布局关键点构造路径点矩阵.如图5所示,选择每个设备的中心点、出入口点和外围边界点,并得到各点的x轴和y轴坐标,通过x轴坐标和y轴坐标交叉组成二维点阵,即可构造一个路径点矩阵.

图5 路径点矩阵构造Fig.5 Path point matrix construction
2) 遍历1)中的路径点矩阵,检测路径点是否与任意设备范围重叠,若存在重叠则将其标记为障碍点,否则标记为可行点.
3) 遍历所有物料的设备路线,调用多目标评估路径搜索算法得到一条最短路径,同时记录路径信息,路径信息包括路径起始点、终点和转弯点参数.
由于输送线路径只允许水平和垂直方向,可能会出现部分线路拐点过多的情况.如图6所示,A→D→C的距离和A→B→C相等,按照原算法的搜索策略会导致两者均可能被选择为路径,为解决该问题,本文进行了以下两步优化:

图6 拐点数不同的多条等长路线Fig.6 Multiple equally long routes with different numbers of turning points
a) 添加路径方向属性Dcur表示当前路径的方向,Dcur有水平和垂直两个取值,每次搜索当前节点的相邻节点时,优先添加方向和Dcur一致的节点;
b) 修改路径搜索的成本评估函数:
F(n)=G(n)+H(n)+E(n).
(11)
其中,G(n)和H(n)为预期路径成本,E(n)为路径转弯成本.这样,在G(n)与H(n)之和相等时,由于转弯点多了E(n)的成本,算法便会优先选择非转弯点加入路径.完成输送线布局后,即可得到所有设备之间的运输距离,再根据式(1)计算出物料搬运总成本.
2.4 处理布局约束
2.4.1 关键设备布局约束
关键设备布局约束如式(3)~(7)所示,包括设备位于车间内约束和设备非重叠约束,前者为线性约束,通过设置每个坐标的上下边界即可实现.后者为非线性约束不好处理.本文综合使用设备位置调整策略和罚函数法处理该约束.
设备位置调整方法如下:
1) 将设备按尺寸从小到大排序;
2) 遍历所有设备,检测是否有重叠情况,若无,进入步骤5),若存在设备与当前设备D1重叠,进入步骤3);
3) 检测第一个与D1重叠的设备,记为D2,通过将D1移出与D2的重叠范围来消除二者的重叠.具体地,规定D1只能向x和y的负方向移动,计算D1在两个方向上的移动距离,并分别计算x轴距离与车间长度、y轴距离与车间宽度的比值,选择比值小的方向作为移动方向,从而避免设备范围溢出车间.通过不断移动D1,消除D1和其他设备的重叠;
4) D1的移动可能会导致新的重叠,如图7(a)所示,设备2在消除与设备3的重叠后,与设备1又发生了重叠.故每次消除D1的重叠后,仍需重新遍历所有设备,并逐一消除重叠,防止顺序在前的设备出现了新的重叠;
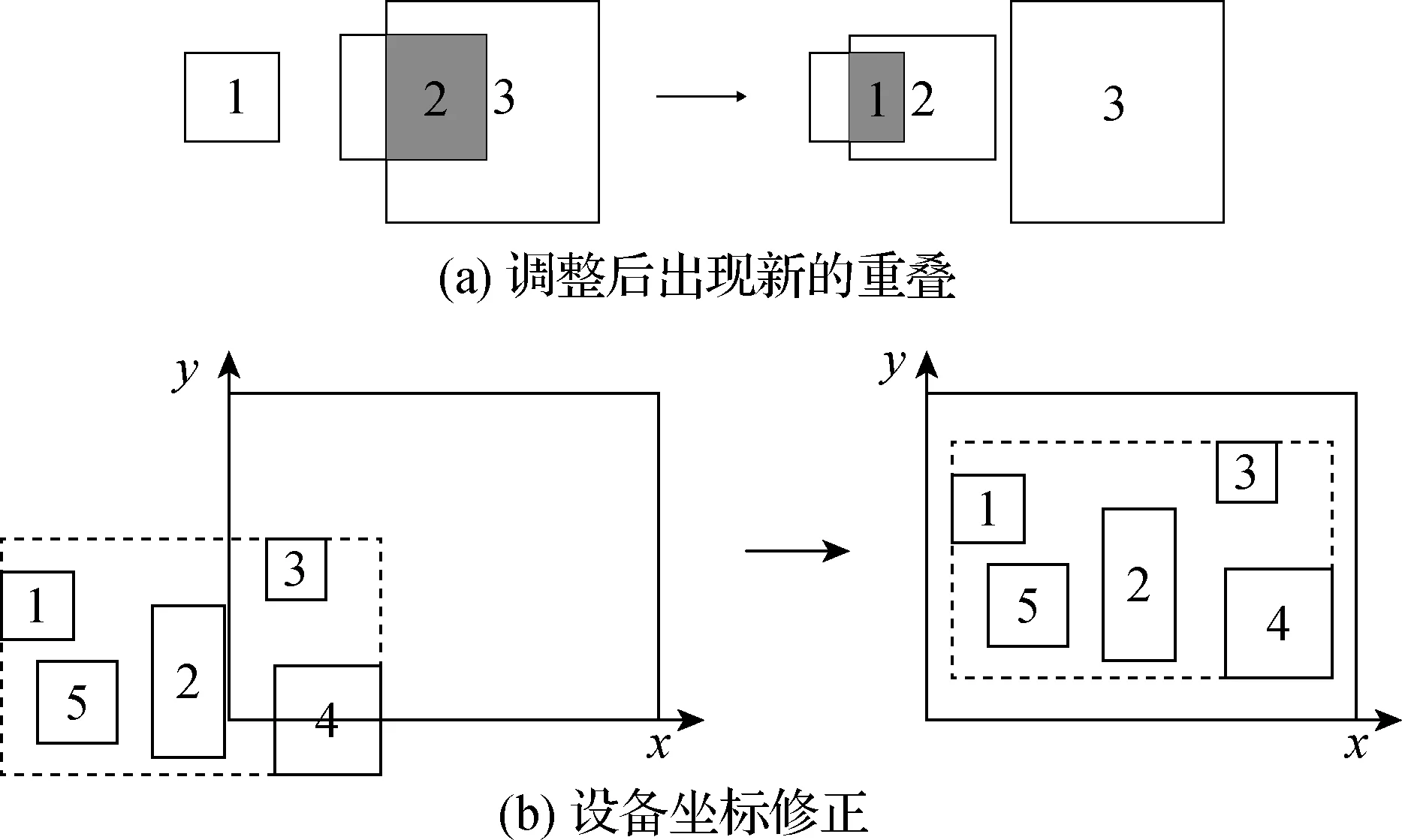
图7 设备重叠调整和坐标修正Fig.7 Overlap adjustment and coordinate correction of device
5) 计算所有设备的总包络矩形范围,在重叠全部消除后,设备的位置可能超出车间范围,如图7(b)所示.若该范围小于车间范围,给包络矩形中心设置一个车间内的随机坐标,并同步修改所有设备的坐标;若范围超出车间范围,调整失败,转而采用罚函数法.
罚函数法是一种常用的处理非线性约束的方法[22].具体的,在1)调整失败后给目标函数设置一个大的正数作为惩罚值.
2.4.2 输送线布局约束
输送线约束如式(8)和(9)所示,本文综合使用设备位置调整策略和罚函数法处理非重叠约束.
首先介绍设备位置调整方法.在本文问题中,不合理的设备布局会导致输送线布局失败.通过归纳设备间各种不合理的相对位置,并针对每种情况制定调整方案,主要是通过移动设备消除不合理位置.图8中列出了部分不合理情况及其调整方案.具体调整过程如下:
1) 取出两个有连接关系的设备,判断两者相对位置是否合理,若不合理,进入步骤2),否则继续步骤1),若所有设备相对位置均合理,调整结束;
2) 根据相对位置的类型选择方案对其进行调整.不同方案的策略相似,即通过平移两个设备,使得输送线中间的不合理部分被消除.以图8(b)中第一个图为例,让两个设备的出入口点在x轴上对齐,即可消除过短的输送线路.接着返回步骤1).

图8 设备间不合理相对位置及其调整Fig.8 Unreasonable relative position of devices and its adjustment
罚函数法则是通过检测所有线路的输送线长度,若发现存在输送线长度过短、输送线之间距离过短的情况,给其目标函数设置一个大的正数作为惩罚值.
3 实验及分析
为了验证本文算法的有效性,本文选择了3个车间布局实例进行实验分析.其中实例1为一个仓储物流车间,其中有若干多入口多出口设备,用于验证本文算法对于解决这类布局问题的有效性.车间详细参数见附录(http:∥jxmu.xmu.edu.cn/upload/20210412.html)表S1和S2.实例2来自于文献[9]中的SFLP-1,实例3来自于文献[2],3个实例的部分参数见附录表S3.由于本文研究的是关键设备与输送线的混合布局,所以对布局数据进行了修改:
1) 添加了输送线参数、设备的出入口参数,输送线参数如附录表S4所示.对于设备出入口参数,除实例1以外,其他实例中设备均设置为单入单出,且出口和入口分别位于设备默认朝向的上方和下方;
2) 除实例1以外,其他实例均没有车间出入口参数;
3) 添加了设备之间的距离约束,具体地,设备4个方向的禁区距离均设为2.5 m;
4) 修改了车间的尺寸,详见附录表S3.
本文分别使用传统设备布局方法(基于MOPSO和NSGA2实现)以及本文中的混合算法(MOPSO-Route和NSGA2-Route)对3个实例进行实验.为保证对比的有效性,控制MOPSO与MOPSO-Route,以及NSGA2与NSGA2-Route的算法参数完全一致.由于传统设备布局方法中不涉及输送线部分,所以只关注物料搬运总成本这一目标.同时,由于传统设备布局方法中输送长度按照理想的曼哈顿距离计算,不符合实际输送线布局,无法直接与本文算法的结果对比.所以使用传统布局算法得到布局结果后,需计算出考虑实际路径下的输送线路长度,然后用该实际长度计算出物料搬运总成本,方可进行对比.
本文算法基于C++实现,对于每个实例,每种算法独立运行10次,然后取平均值,结果如表2所示.表3给出了每种算法运行10次的平均运行时间.图9中给出了每种算法的部分布局结果图.

表2 实例1~3在4种算法下的实验结果Tab.2 The experimental results of example 1-3 under four algorithms
由表2可知,在3个实例的实验中,本文的两种混合算法的布局结果均优于传统设备布局算法.
分析表3结果,由于混合布局算法结合了多目标优化算法和基于路径搜索的布线算法,所以其计算时间较长.混合布局算法中,较耗时的操作主要包括每次迭代时解的更新和布线过程.且根据表中数据可知,在迭代次数相同时,NSGA2-Route算法的运行效率要低于MOPSO-Route算法.
分析图9结果,混合算法布局结果满足了设备和输送线的各项约束;从图9中的圆圈标记处可以看出,传统方法得到的布局会出现输送线路长度过短、输送线之间发生冲突的情况,其布局结果不具有可行性.

图9 混合算法布局结果Fig.9 Hybrid algorithm layout results
4 结论和展望
物流场景中同时存在关键设备和输送线设备,而传统设备布局方法中只适用于关键设备的布局.本文针对该问题,提出了一个结合多目标元启发式优化方法和布线算法的混合布局算法框架,同时针对设备位置连续变化和混合布局的特点,提出了处理关键设备和输送线约束的策略.接着,本文分别使用MOPSO和NSGA2作为元启发式算法,使用改进的多目标评估的路径搜索算法作为布线算法,在混合算法框架下实现了MOPSO-Route和NSGA2-Route两个具体算法,并通过与传统设备布局算法(基于MOPSO[7]和NSGA2[21])的对比,验证了本文算法在解决物流场景中混合布局问题上的优越性.未来可以进一步提高算法效率,实现对于更大规模物流场景的高效布局.

表3 算法运行时间

