基于“问题+追问”教学法的教学案例及思考

陈旭旋

2019年12月，广東教育学会中学数学教学专业委员会发出《关于征集第二届广东省中考数学疑难问题教学设计的通知》，笔者有幸参加了此次的教学设计评选。在经过对中考数学疑难问题的认真分析研究下，笔者选择了压轴题高频考点：由动点产生的特殊三角形的存在性问题之等腰三角形存在性问题作为课例，采用“问题+追问”的启发引导教学法进行教学设计，经过中数会组织的专家评审中获得特等奖。现将其教学设计过程和反思整理出来，以抛砖引玉，欢迎各位同行和专家批评指正。

一、教学案例--以等腰三角形的存在性问题为例

1.问题引入

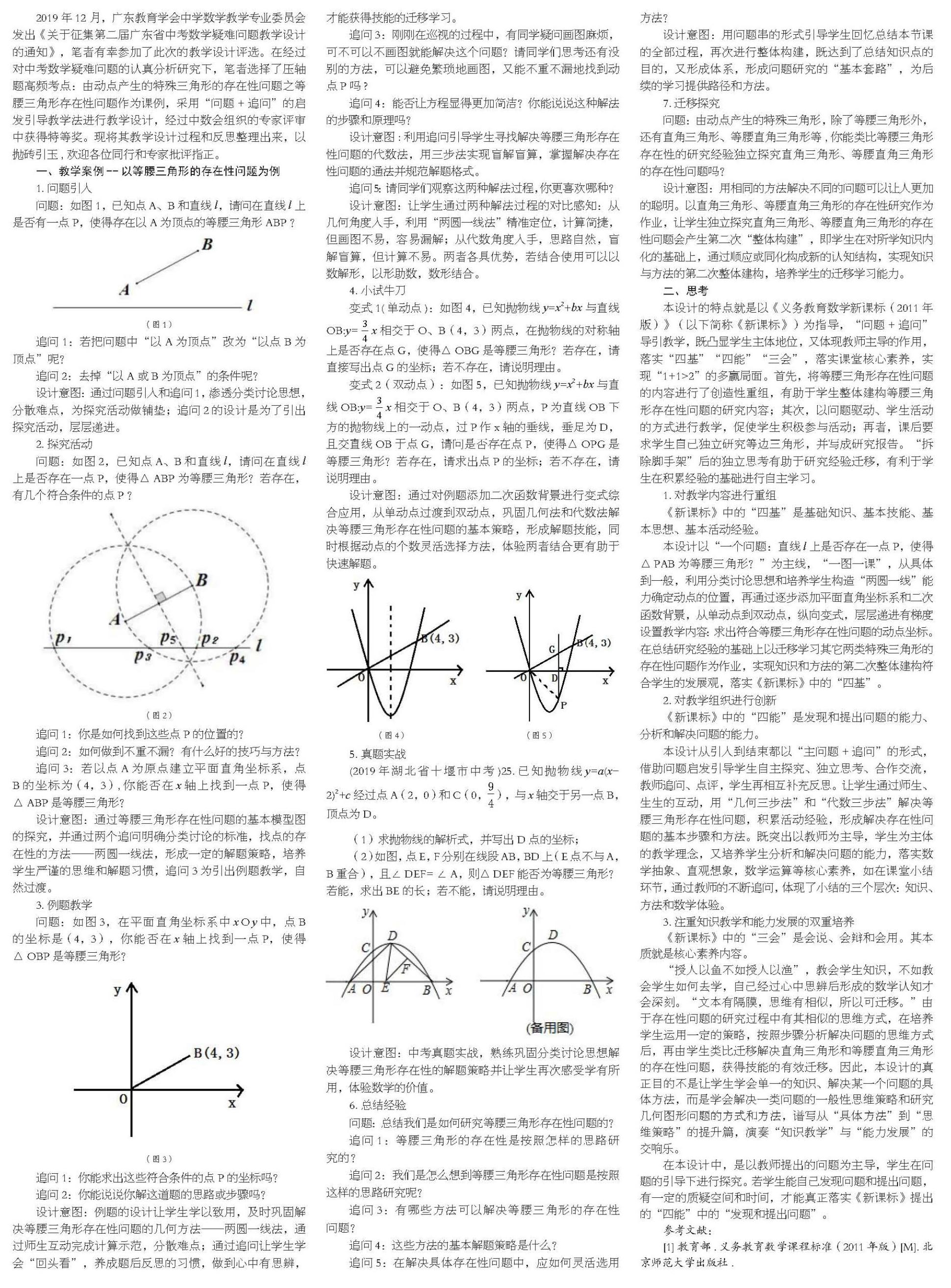
问题：如图1，已知点A、B和直线l，请问在直线l上是否有一点P，使得存在以A为顶点的等腰三角形ABP？

追问1：若把问题中“以A为顶点”改为“以点B为顶点”呢？

追问2：去掉“以A或B为顶点”的条件呢？

设计意图：通过问题引入和追问1，渗透分类讨论思想，分散难点，为探究活动做铺垫;追问2的设计是为了引出探究活动，层层递进。

2.探究活动

问题：如图2，已知点A、B和直线l，请问在直线l上是否存在一点P，使得△ABP为等腰三角形？若存在，有几个符合条件的点P？

追问1：你是如何找到这些点P的位置的？

追问2：如何做到不重不漏？有什么好的技巧与方法？

追问3：若以点A为原点建立平面直角坐标系，点B的坐标为（4，3），你能否在x轴上找到一点P，使得△ABP是等腰三角形？

设计意图：通过等腰三角形存在性问题的基本模型图的探究，并通过两个追问明确分类讨论的标准，找点的存在性的方法——两圆一线法，形成一定的解题策略，培养学生严谨的思维和解题习惯，追问3为引出例题教学，自然过渡。

3.例题教学

问题：如图3，在平面直角坐标系中x O y中，点B的坐标是（4，3），你能否在x轴上找到一点P，使得△OBP是等腰三角形？

追问1：你能求出这些符合条件的点P的坐标吗？

追问2：你能说说你解这道题的思路或步骤吗？

设计意图：例题的设计让学生学以致用，及时巩固解决等腰三角形存在性问题的几何方法——两圆一线法，通过师生互动完成计算示范，分散难点;通过追问让学生学会“回头看”，养成题后反思的习惯，做到心中有思辨，才能获得技能的迁移学习。

追问3：刚刚在巡视的过程中，有同学疑问画图麻烦，可不可以不画图就能解决这个问题？请同学们思考还有没别的方法，可以避免繁琐地画图，又能不重不漏地找到动点P吗？

追问4：能否让方程显得更加简洁？你能说说这种解法的步骤和原理吗？

设计意图：利用追问引导学生寻找解决等腰三角形存在性问题的代数法，用三步法实现盲解盲算，掌握解决存在性问题的通法并规范解题格式。

追问5：请同学们观察这两种解法过程，你更喜欢哪种？

设计意图：让学生通过两种解法过程的对比感知：从几何角度入手，利用“两圆一线法”精准定位，计算简捷，但画图不易，容易漏解;从代数角度入手，思路自然，盲解盲算，但计算不易。两者各具优势，若结合使用可以以数解形，以形助数，数形结合。

4.小试牛刀

变式1（单动点）：如图4，已知抛物线y=x2+bx与直线OB：y=x相交于O、B（4，3）两点，在抛物线的对称轴上是否存在点G，使得△OBG是等腰三角形？若存在，请直接写出点G的坐标;若不存在，请说明理由。

变式2（双动点）：如图5，已知抛物线y=x2+bx与直线OB：y=x相交于O、B（4，3）两点，P为直线OB下方的抛物线上的一动点，过P作x轴的垂线，垂足为D，且交直线OB于点G，请问是否存在点P，使得△OPG是等腰三角形？若存在，请求出点P的坐标;若不存在，请说明理由。

设计意图：通过对例题添加二次函数背景进行变式综合应用，从单动点过渡到双动点，巩固几何法和代数法解决等腰三角形存在性问题的基本策略，形成解题技能，同时根据动点的个数灵活选择方法，体验两者结合更有助于快速解题。

5.真题实战

（2019年湖北省十堰市中考）25.已知抛物线y=a（x-2）2+c经过点A（2，0）和C（0，），与x轴交于另一点B，顶点为D。

（1）求抛物线的解析式，并写出D点的坐标;

（2）如图，点E，F分别在线段AB，BD上（E点不与A，B重合），且∠DEF=∠A，则△DEF能否为等腰三角形？若能，求出BE的长;若不能，请说明理由。

设计意图：中考真题实战，熟练巩固分类讨论思想解决等腰三角形存在性的解题策略并让学生再次感受学有所用，体验数学的价值。

6.总结经验

问题：总结我们是如何研究等腰三角形存在性问题的？

追问1：等腰三角形的存在性是按照怎样的思路研究的？

追问2：我们是怎么想到等腰三角形存在性问题是按照这样的思路研究呢？

追问3：有哪些方法可以解决等腰三角形的存在性问题？

追问4：这些方法的基本解题策略是什么？

追问5：在解决具体存在性问题中，应如何灵活选用方法？

设计意图：用问题串的形式引导学生回忆总结本节课的全部过程，再次进行整体构建，既达到了总结知识点的目的，又形成体系，形成问题研究的“基本套路”，为后续的学习提供路径和方法。

7.迁移探究

问题：由动点产生的特殊三角形，除了等腰三角形外，还有直角三角形、等腰直角三角形等， 你能类比等腰三角形存在性的研究经验独立探究直角三角形、等腰直角三角形的存在性问题吗？

设计意图：用相同的方法解决不同的问题可以让人更加的聪明。以直角三角形、等腰直角三角形的存在性研究作为作业，让学生独立探究直角三角形、等腰直角三角形的存在性问题会产生第二次“整体构建”，即学生在对所学知识内化的基础上，通过顺应或同化构成新的认知结构，实现知识与方法的第二次整体建构，培养学生的迁移学习能力。