单箱三室连续梁桥在横向温度梯度与汽车偏载下的空间效应分析

刘金春，宋子轩，梁 栋

(河北工业大学 土木与交通学院，天津 300401)

0 引 言

为适应我国车流量逐渐增大，交通运输负担逐渐加重的变化趋势，桥梁宽度不断地增加，具有宽箱结构的连续梁桥由于变形小、施工技术成熟、运营行车舒适等优点被广泛应用。但在其实际运营中出现的裂缝问题日趋严重[1-3]。一方面原因是对温度梯度作用的认识还存在着不足，在以往箱梁桥设计中往往忽略横向温度梯度作用；另一方面原因是宽箱梁作为一种典型的空间薄壁结构[4]，在汽车偏载作用下产生的空间效应不可忽视，尽管在设计计算时会引入偏载增大系数来考虑荷载放大效应，但不论经验系数法、偏心压力法还是修正的偏心压力法在计算宽箱梁桥的偏载增大系数时均具有一定的局限性[5]，无法准确计算得到宽箱梁结构在汽车偏载下的空间效应。

针对上述两方面原因科研人员也做了相关研究：随着对温度梯度作用及其效应研究的深入，发现某些箱梁桥的温度梯度作用效应逐渐达到甚至超过汽车荷载效应[6-8]；张广达等[9]利用ANSYS有限元软件建立了桥宽25 m的宽箱连续梁桥实体有限元模型，分别布置JTGD60—2015《公路桥涵通用设计规范》中的温度梯度作用与JTGD60—2004《公路桥涵通用设计规范》中的温度梯度作用计算得到，前者的作用效应比后者的作用效应更加贴近实际；陈国强[10]利用有限元软件对桥宽33 m的宽箱连续梁桥分析得到，以往单箱单室箱梁桥设计计算时采用的偏载增大系数已不能适用于宽箱连续梁桥，需要根据实际桥型建立实体有限元模型进行重新计算；马兆锐等[11]通过对桥宽16 m的宽箱连续梁桥分别采用梁单元和实体单元建立模型分析移动荷载效应，得到梁单元模型计算结果安全储备较小，应按照实体单元模型计算。

由于JTGD60—2015《公路桥涵通用设计规范》中新增的横向温度梯度作用是参考“超大跨混合斜拉桥”项目的研究成果制定的，并建议对于无悬臂的宽幅箱梁桥宜考虑横向温度梯度作用，而对于有悬臂的宽幅箱梁桥是否存在规范中规定的横向温度梯度作用，以及规范中横向温度梯度作用参考值是否适用于全国各地，需要对实桥进行实测，通过温度数据的采集与分析得到。目前关于宽箱连续梁桥同时考虑在横向温度梯度作用和汽车偏载下的空间效应的研究较少。

笔者以某单箱三室连续梁桥为工程依托，该桥顶板宽25.4 m，基于现场实测温度数据，拟合得到实测横向温度梯度作用，利用midas/FEA有限元软件建立了全桥实体有限元模型，分析在实测横向温度梯度作用和汽车偏载下的空间效应，为同地区类似结构的设计与计算提供参考。

1 工程概况及有限元模型

某单箱三室连续梁桥位于河北省廊坊市境内，呈南北走向。跨度(45+80+45)m，顶板宽25.4 m，底板宽19.5 m，翼缘板宽2.95 m，箱室高度由支点处4.7 m变化到跨中处2.2 m。全桥及典型截面示意图如图1，其中在图1(a)中截面A-A为中跨跨中截面，截面B-B为中跨支点截面，截面C-C为边跨跨中截面。

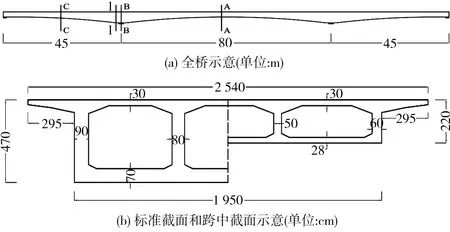
图1 全桥及典型截面示意Fig.1 Schematic diagram of the whole bridge and typical cross- sections

利用midas/Civil有限元软件建立全桥上部结构的杆系有限元模型，共计65个节点，54个单元。具体材料参数如下表1和表2。

表1 C50混凝土主要力学参数Table 1 Main mechanical parameters of C50 concrete

表2 预应力钢筋力学性能和相关计算参数Table 2 The mechanical properties and the relevant calculation parameters of prestressing tendon

通过midas/Civil有限元软件中杆系模型转为实体模型功能，将上部结构杆系模型导入到midas/FEA有限元软件中，建立全桥上部结构实体有限元模型，以边跨端部截面的顶板上缘中点为坐标原点建立全桥空间直角坐标系，其中X轴方向为纵桥向，Y轴方向为横桥向，Z轴方向为竖桥向。材料参数，边界条件均与杆系有限元模型设置一致，并以0.5 m尺寸的六面体单元划分网格，共划分108 084个节点，100 643个单元。全桥和截面A-A网格划分如图2。

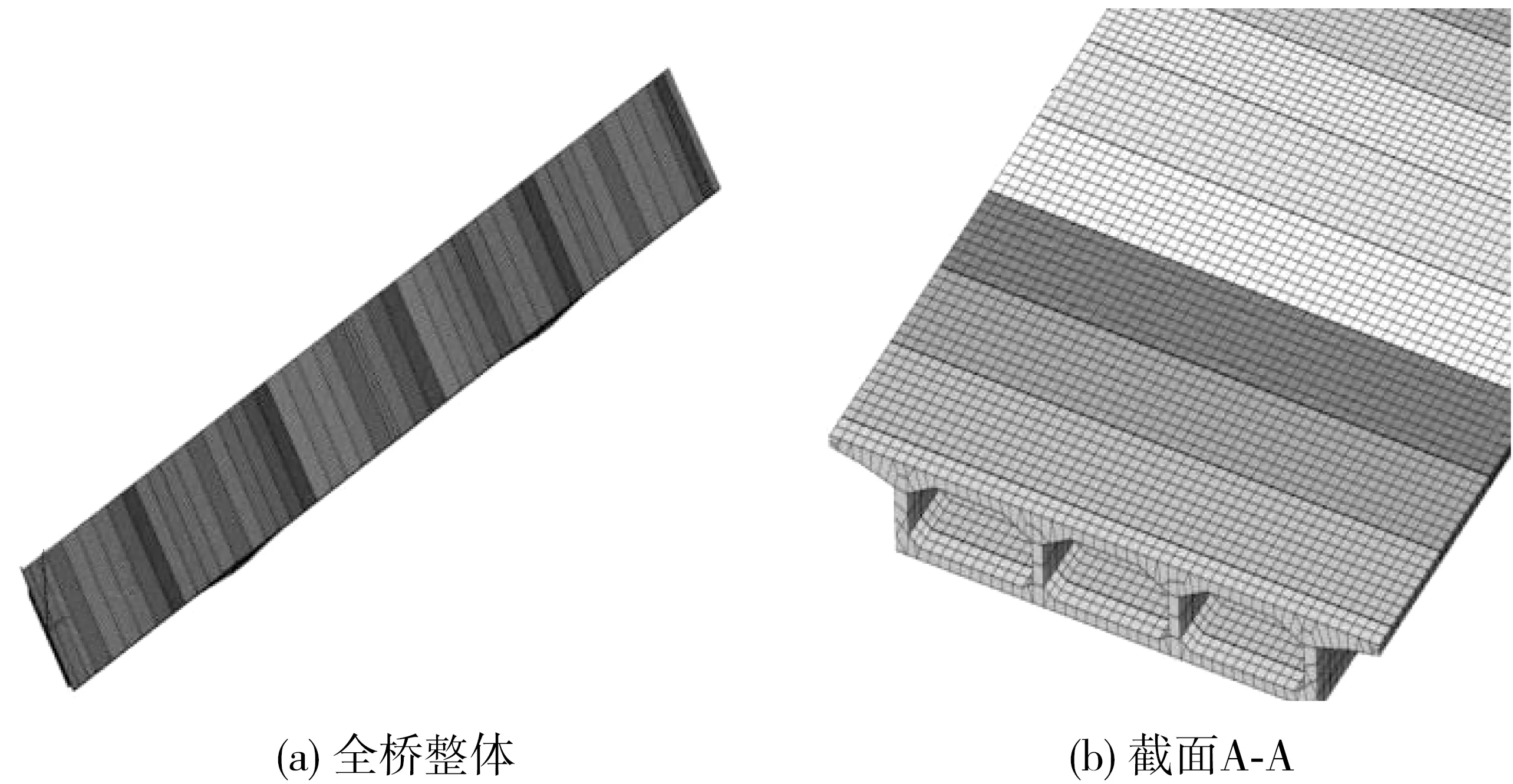
图2 实体有限元模型网格划分Fig.2 Mesh generation of solid finite element model

2 横向温度梯度作用效应分析

2.1 箱梁日照温度场的实测

箱梁日照温度场是随时发生变化的，由文献[12]得到，沿桥纵向不同位置、不同高度的箱梁截面具有相同的温度分布形式，因此将箱梁日照温度场由三维空间问题简化为二维平面问题。选择4#桥墩的0#梁段端部截面1-1如图1(a)，在施工阶段预埋温度传感器如图3(a)，通过连接自动采集仪如图3(b)采集温度数据，时间间隔设定2 h。截面温度测点布置如图4，其中T1～T5为顶板温度测点，M1～M4为腹板温度测点，B1～B3为底板温度测点。

图3 温度场数据采集仪器Fig.3 Temperature field data acquisition instrument

图4 截面温度传感器布置(单位：cm)Fig. 4 Arrangement of temperature sensors at cross-section

箱梁日照温度场主要受到太阳辐射、大气温度、风速这3个主要因素影响[13]，故筛选箱梁温度实测数据时，优先选择晴天，无风且温差较大的典型日期下温度实测数据，最终确定2019年9月6日至9月8日的温度数据。将顶板、腹板、底板测点温度随时间变化的数据整理后发现只有顶板具有较大的横向温度梯度，现将顶板温度传感器测点温度随时间变化的数据整理如图5。

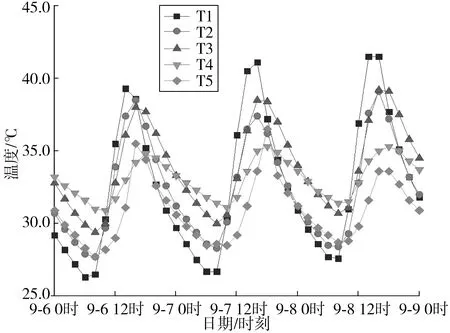
图5 顶板温度传感器测点温度值随时间变化曲线Fig.5 Curve of temperature value of the measured point of roof temperature sensor changing with time

由图5可得，顶板各测点温度随时间变化规律类似正弦曲线，每天均在14：00时达到最大温度，同时刻顶板也达到最大横向温度梯度。

2.2 实测横向温度梯度作用曲线的拟合

选择2019年9月8日14:00时刻顶板各测点温度数据，根据JTGD60—2015《公路桥涵通用设计规范》中4.3.12条第4点的条文说明所给出的横向温度梯度作用曲线类型为线性，利用最小二乘法拟合得到实测横向温度梯度作用曲线如图6，其中T1为10.2 ℃，B为顶板宽。

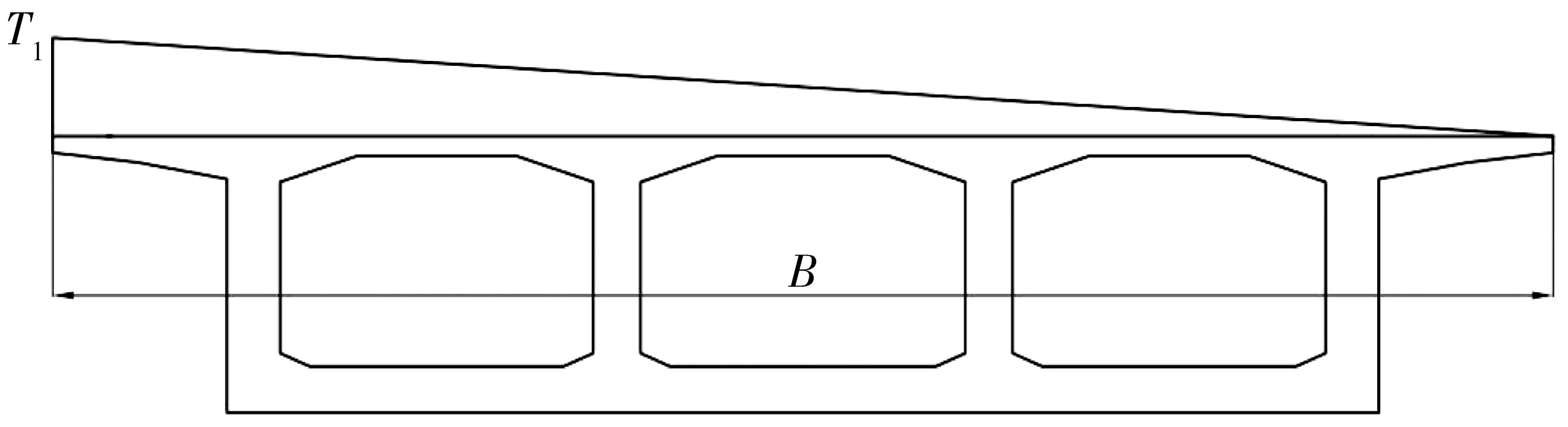
图6 横向温度梯度作用曲线Fig.6 Transverse temperature gradient effect curve

2.3 横向温度梯度作用效应的计算结果与分析

将2.2节拟合得到的横向温度梯度作用加载于实体有限元模型中的顶板位置，由于各截面受到的横向温度梯度作用是相同的，因此选择分析中跨支点(截面B-B)和中跨跨中(截面A-A)的横向温度梯度作用效应。将两个截面的最大与最小应力值整理如表3，其中拉应力为正，压应力为负。

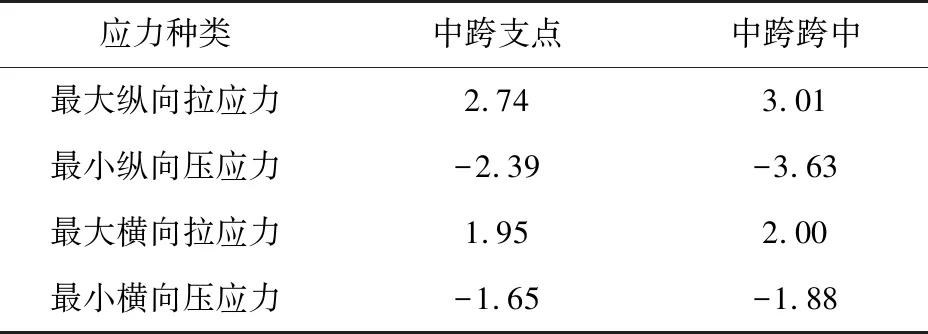
表3 截面最大与最小应力值Table 3 Maximum and minimum stress values at cross-section MPa

通过对比表3中的中跨支点与中跨跨中最大应力值可得：中跨跨中在受到实测横向温度梯度作用时产生的最大应力值明显比中跨支点的大。因此，中跨跨中截面是在横向温度梯度作用下的最不利截面位置。

计算得到中跨跨中截面的竖向与横向位移分布图如图7，其中分布图的右侧为上述定义Y轴的正方向侧，竖向位移向上为正，向下为负；横向位移向右为正，向左为负。

图7 截面A-A位移分布(单位：m)Fig. 7 Displacement distribution of cross-section A-A

由图7可得，中跨跨中截面竖向位移在Y轴正方向是向下的，而在Y轴负方向处是向上的，竖向位移沿桥宽方向变化不均匀，在Y轴正方向的翼缘板端部取得最大竖向位移3.95 cm，在Y轴负方向的翼缘板端部取得最小竖向位移-2.18 cm；横向位移整体偏向Y轴正方向，在Y轴正方向的翼缘板端部达到最大横向位移1.39 cm。

3 汽车偏载效应分析

该桥设计荷载为公路-Ⅰ级，单向通行。根据JTGD60—2015《公路桥涵通用设计规范》中4.3.1条关于汽车荷载的规定布置车道荷载，其荷载示意如图8，其中均布荷载标准值qk取10.5 kN/m，集中荷载标准值Pk取360 kN；设计车道数为单向七车道，车道横向具体布置示意如图9，并考虑多车道横向折减系数。

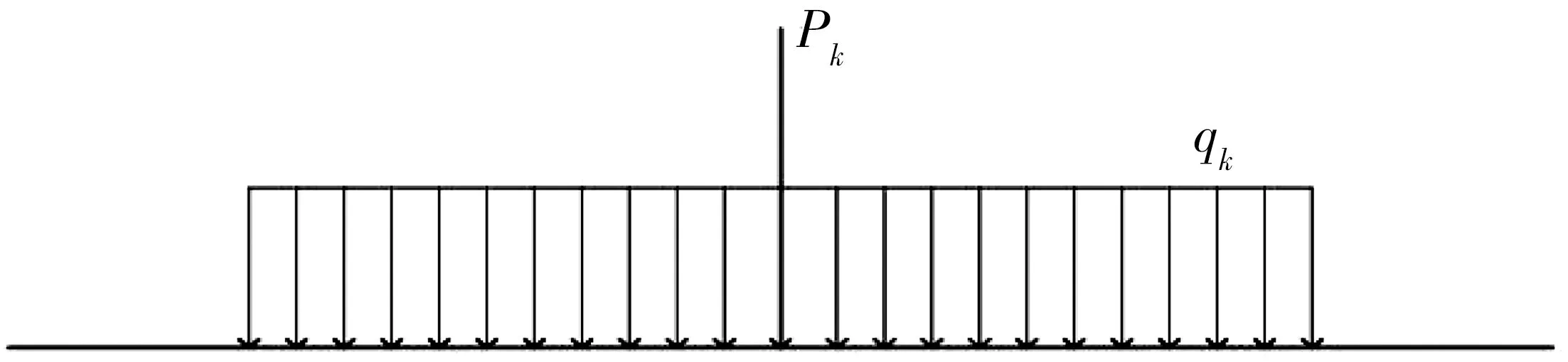
图8 车道荷载Fig.8 The lane load

图9 车道荷载横向布置(单位：m)Fig. 9 Transverse arrangement of the lane load

3.1 汽车偏载的布置

目前midas/FEA无法直接布置汽车荷载，并自动按照影响线或影响面的方法计算得到相应的荷载效应。因此首先通过midas/Civil按照上述车道荷载布置，计算得到汽车偏载下全桥竖向弯矩My图，如图10。

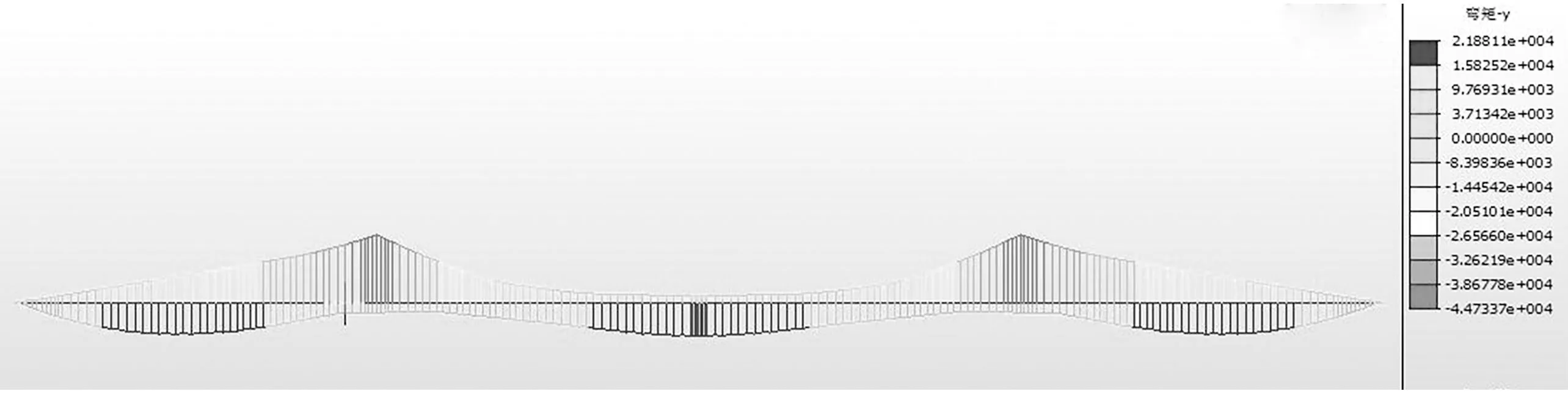
图10 车道偏载作用下全桥竖向弯矩My(单位：kN·m)Fig. 10 Vertical bending moment My of the whole bridge under eccentric lane load

由图10可得，最大负弯矩出现在中跨支点截面，最大正弯矩出现在中跨跨中截面，虽然边跨跨中截面的正弯矩值与中跨跨中截面的十分接近，但二者截面存在较大差异。对于混凝土结构来说，开裂往往是由于拉应力过大引起的，因此选择中跨跨中底板和中跨支点顶板作为分析偏载效应的最不利截面位置，接下来利用midas/Civil中移动荷载追踪器功能得到上述两个截面达到最大弯矩时的影响线，根据影响线形状，在midas/FEA中利用点荷载和均布荷载布置对应的车道荷载，其中车道荷载横向布置均按照图9，由Y轴正方向向负方向布置，并依据车道加载数量的不同分为不同的计算工况，如表4，车道荷载纵向布置如图11。

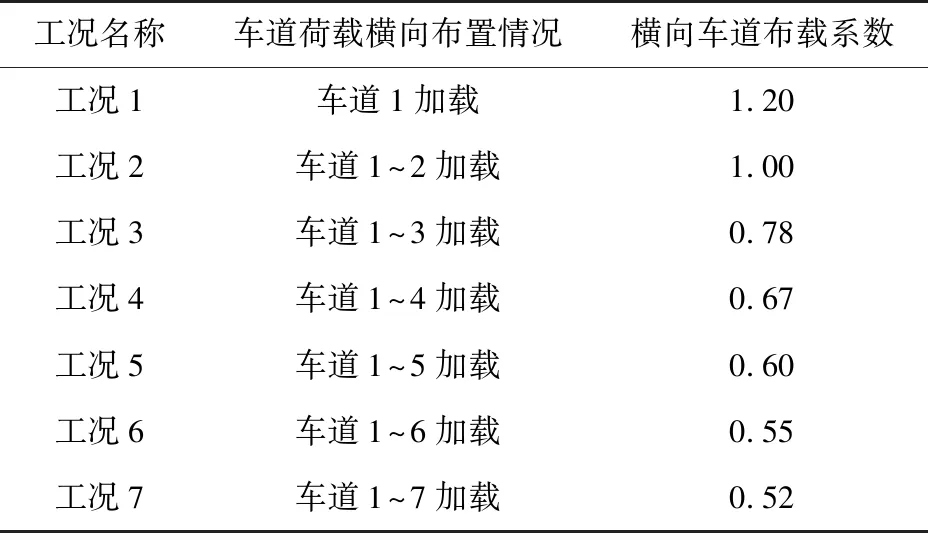
表4 计算工况Table 4 Calculation condition

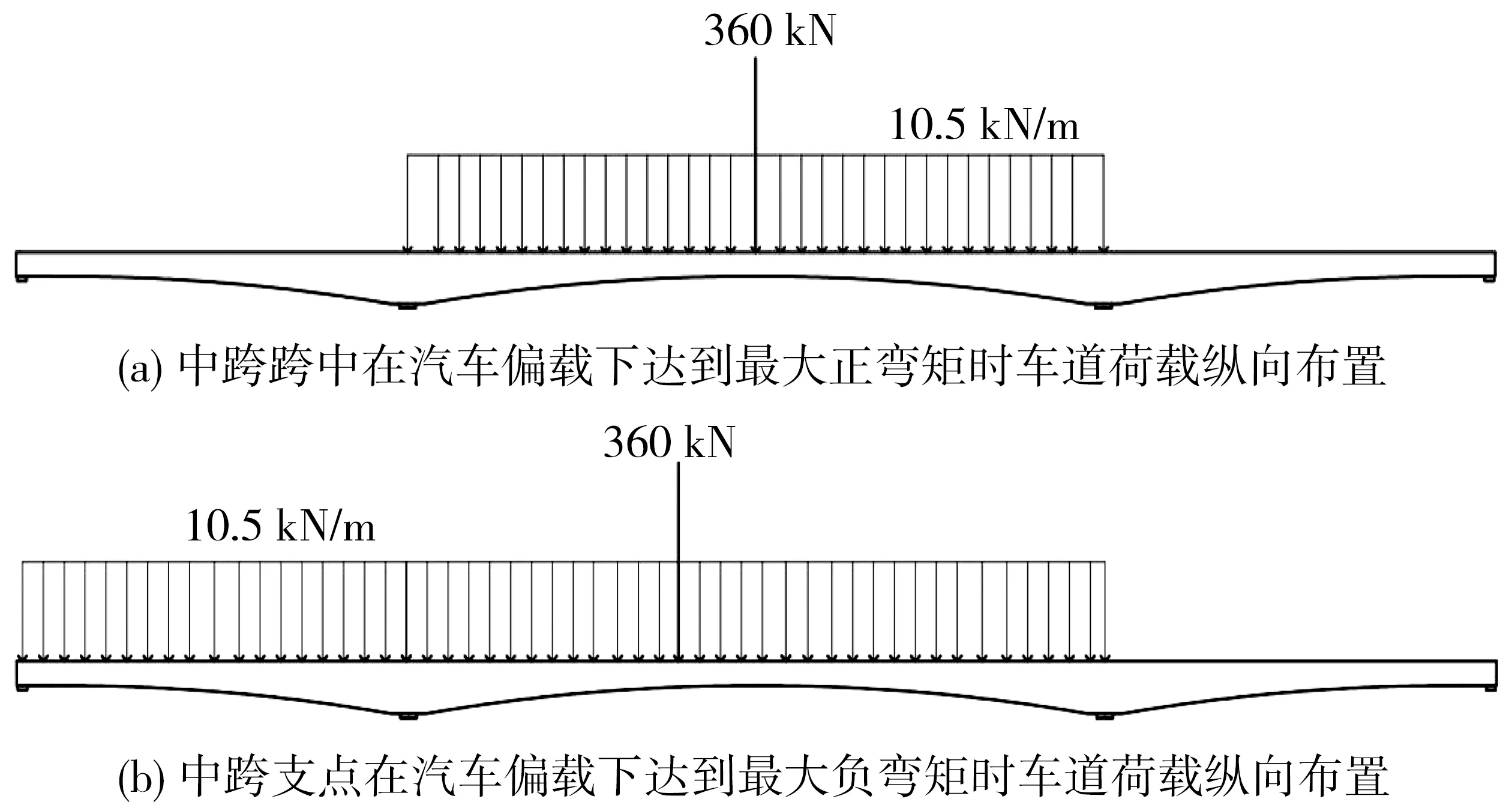
图11 车道荷载纵向布置Fig.11 Longitudinal arrangement of the lane load

3.2 汽车偏载效应的计算结果

中跨跨中(截面A-A)底板下缘，中跨支点(截面B-B)顶板上缘在各工况下的纵向应力和横向应力分布结果分别如图12和图13，图中横向坐标零点表示为顶板或底板宽度的中心；竖向坐标轴表示应力值，其中拉应力为正，压应力为负。

图13 截面B-B顶板上缘在各工况下应力分布Fig.13 Stress distribution of of the upper edge of top slab of cross-section B-B under different loads

由图12可得，考虑横向车道布载系数后得到的中跨跨中底板下缘纵向应力和横向应力均以底板中心线大致呈反对称分布。各工况下的最大纵向拉应力均在底板正向边缘处取得，工况2下取得纵向拉应力最大值，达到4.66 MPa，但工况3与工况4下的最大纵向拉应力与工况2下的较为接近；各工况下的最大横向拉应力出现位置不同，在工况1、工况2下出现在边箱室倒角下侧；在工况3～工况5下，出现在中箱室倒角(横向坐标轴正向)下侧；在工况6、工况7下，出现在中箱室倒角(横向坐标轴负向)下侧，横向拉应力最大值在工况4下取得，达到1.38 MPa。

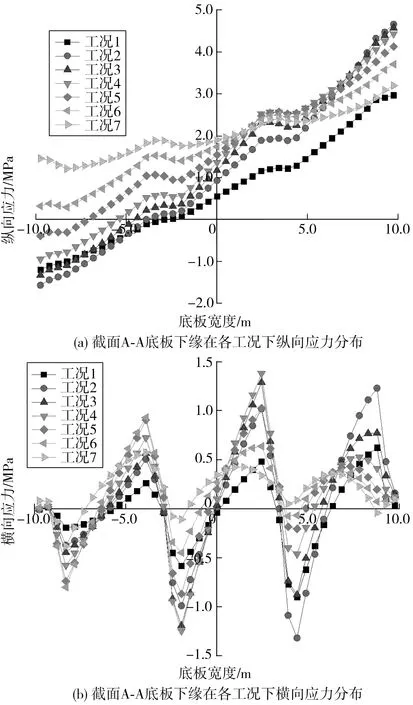
图12 截面A-A底板下缘在各工况下应力分布Fig.12 Stress distribution of the lower edge of bottom slab of cross-section A-A under different loads

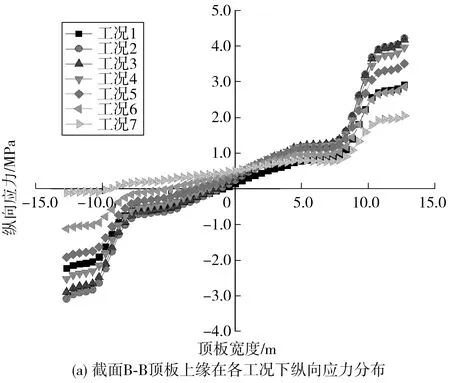
由图13可得，考虑横向车道布载系数后得到的中跨支点顶板上缘纵向应力和横向应力均以顶板中心线大致呈反对称分布。各工况下的最大纵向拉应力均出现在顶板正向端部，并且随着车道荷载的增加，纵向应力沿顶板分布曲线更加平缓，其中最大纵向拉应力在工况2下取得，达到4.23 MPa；各工况下的最大横向拉应力均在顶板中心线靠近正向附近取得，但数值均很小，最大横向拉应力在工况2、工况3下取得，均为0.45 MPa。

3.3 汽车偏载效应计算结果的分析

分别比较图12(a)和图13(a)以及图12(b)和图13(b)可以得到，中跨跨中底板下缘达到最大纵向应力与中跨支点顶板上缘取得最大纵向应力所在工况均为工况2，但在达到最大横向应力时两个位置所在的工况时却不一致，中跨跨中底板下缘在工况4下取得而中跨支点顶板上缘在工况2、工况3下取得，但不论是纵向应力还是横向应力，中跨跨中底板下缘的最大应力值均大于中跨支点顶板上缘的最大应力值，尤其是最大横向应力，中跨跨中底板下缘的最大横向应力值为中跨支点顶板上缘的3.1倍，因此中跨跨中底板为汽车偏载下的最不利截面位置。

中跨跨中底板处在工况2～工况4下最大应力值较为接近，其中工况2达到最大纵向应力值，与工况4下的最大纵向应力值相差不到5%，但工况4下达到最大横向应力值，与工况2下的最大横向应力值相差大于10%。一方面由于横向应力在各工况下变化幅度较大，另一方面由于纵向预应力筋的布置会对横桥向抗拉强度产生一定程度的削弱，故选择工况4作为最不利汽车偏载工况。

4 横向温度梯度作用与汽车偏载下的空间效应组合

对单箱三室连续梁桥中跨跨中底板处在实测横向温度梯度作用和按照工况4布置的汽车偏载下的空间效应进行组合。结合JTG 3362—2018《公路钢筋混凝土及预应力桥涵设计规范》中对于预应力混凝土构件抗裂验算的要求，以判断构件混凝土拉应力是否超过规定的限值。参考A类部分预应力混凝土构件在作用(或荷载)短期效应组合，构件正截面混凝土的拉应力应满足式(1)：

σst-σpc≤0.7ftk

(1)

式中：σst为按作用(或荷载)短期效应组合计算的构件抗裂验算边缘混凝土法向拉应力；σpc为预加力作用下受弯构件抗裂验算边缘混凝土的预压应力；ftk为混凝土轴心抗拉强度标准值。

作用短期效应组合是永久作用标准值效应与可变作用频遇值效应的组合，其中汽车荷载(不含冲击力)的频遇值系数为0.7，温度梯度作用的频遇值系数为0.8；本桥采用C50混凝土，0.7ftk=1.86 MPa。组合后的中跨跨中底板下缘的最大纵向应力与最大横向应力值如表5，除σpc的应力数值是以压应力为正，其余项均以拉应力为正。

表5 中跨跨中底板下缘荷载效应组合后的最大纵向应力与横向应力Table 5 The maximum longitudinal stress and transverse stress after load effect combination at the lower edge of the bottom slab of the mid-span of the central span MPa

由表5可得，无论是纵向应力还是横向应力计算结果已经远大于0.7倍的混凝土轴心抗拉强度标准值。中跨跨中底板下缘处在实测横向温度梯度作用和汽车偏载下的空间效应组合后的最大应力已不满足规范中关于抗裂验算的要求。

5 结 论

为得到单箱三室连续梁桥在横向温度梯度作用和汽车偏载下的空间效应，依托某单箱三室连续梁桥实际工程，通过实测温度数据拟合得到符合当地气候条件的实测横向温度梯度作用曲线，利用midas/FEA有限元软件建立实体有限元模型，分别计算横向温度梯度作用效应和汽车偏载效应，并将二者进行荷载效应组合。通过计算分析得到以下结论：

1)由实测温度数据可知，单箱三室连续梁桥在顶板处存在着较大的横向温度梯度作用，其作用曲线类型与JTGD60—2015《公路桥涵通用设计规范》中类似，但特征值远大于后者。因此，建议设计类似桥型时，应慎重考虑其横向温度梯度作用特征值，必要时应通过实测获取相应数据。

2)单箱三室变截面连续梁桥在汽车偏载下中跨跨中底板处为最不利截面位置，最不利汽车偏载为汽车荷载布置于桥宽一半的情况。

3)将文中的单箱三室连续梁桥在横向温度梯度作用和汽车偏载下的空间效应组合后，已不满足规范关于A类部分预应力混凝土构件的抗裂要求。因此，单箱三室连续梁桥在设计计算时需要对上述两种荷载效应进行充分考虑。