基于FFOS-ELM和PF的短时交通流自适应预测模型

王 涛，谢思红，黎文皓,2，李文勇

(1.桂林电子科技大学 建筑与交通工程学院，广西 桂林 541004；2.东南大学 交通学院，江苏 南京 210096)

0 引 言

随着智能交通系统的发展，交通控制以及实时交通诱导已经成为交通领域研究的热点[1]。而对于交通控制和实时交通诱导来说，交通流预测的准确性和可靠性是其实现的必要条件和重要基础。对于交通流预测而言，按照预测时间范围划分可以分为长期交通流预测和短时交通流预测，其中短时交通流预测显得更为重要。短时交通流预测，为智能交通系统的核心内容，指的是根据由时间序列获取的道路交通流量数据预测未来较短时间段内(一般跨度不超过15 min)的交通流情况[2]，是智能交通系统中各个子系统功能实现的基础。相比较长期交通流预测，短时交通流预测由于预测的时间跨度比较短，交通流表现出较不明显的规律性，对预测方法提出了更高的要求。

一些研究者们首先提出将短时交通流量预测视为时间序列的线性问题进行分析[3]，接着国内外的研究人员根据不同领域的方法设计出了多种交通流预测模型。这些方法大致可分为线性模型、非线性模型、混合模型和其它模型4种类型。第一类是传统的线性预测模型，主要包括自回归模型[4](AR,autoregressive model)、差分整合移动平均自回归模型[5-7](ARIMA,autoregressive integrated moving average model)等时间序列模型以及卡尔曼滤波(KF,Kalman filtering)模型[8-9]。第二类是非线性模型，是根据大量的历史观测数据分析出交通流系统运动的规律，通过监督学习获得交通流的预测模型。比较有代表性的有非参数回归模型[10-11]、支持向量机模型[12-13]和神经网络模型[14-16]等。第三类是混合模型，是指使用两种或两种以上的模型进行交通流预测，是目前最常使用的短时交通流预测方法。其主要形式为将一种模型的输出结果作为另一种模型的输入，通过模型衔接得到最终结果，或是同时对多种模型进行预测，通过合并改进实现整个预测结果的优化[17]。第四类是交通仿真模型、动态交通分配模型等其它模型。交通仿真是通过对信号控制规律、道路网络和交通量进行模拟，从而掌握道路网络未来的发展变化与高可能性的发展状态。交通仿真系统分为宏观、中观和微观3类，其中将微观仿真与动态交通分配结合的方法在短时交通流预测中应用较广[18]。

但是，长久以来学者们并没有意识到短时交通流存在的高度非线性和不确定性问题及其对交通流状态的影响。直到近年，才有研究者开始对交通流不确定性进行研究，并先后提出将模糊理论和混沌理论用于交通领域的不确定性问题研究。ZHANG Yunlong等[19]使用模糊逻辑系统方法试图解释各种突发情况下的交通状态变化，以得到准确和稳定的预测结果；XUE Jieni等[20]提出了一种基于混沌时间序列分析方法的短时交通流预测模型，针对交通流复杂的结构，利用交通流数据进行相空间重构，并通过优化得到预测模型。同时，针对单一模型的局限性，多测度组合模型也逐渐被用于解决交通流预测的不确定性问题，包括模糊理论、卡尔曼滤波与神经网络的组合预测模型[21]、混沌理论与支持向量机的多测度组合预测模型[22]等。这些方法虽然在一定程度上解决了交通流不确定性的影响，但因交通流具有复杂非线性结构，很难建立一个准确的模型来描述。

笔者试图从交通系统整体出发，挖掘交通流内在复杂的结构，通过增量学习方法实时更新预测模型参数来适应交通流不确定性变化，同时与非线性滤波的抗干扰、高精度的滤波能力相结合，提出一种自适应实时预测模型。该模型以历史和现有数据为依据，通过带遗忘因子的极限学习机在线实时更新模型，从而可以构建一个长期变化的模型来预测未来交通量的变化趋势，再利用粒子滤波得到最优的交通量短时变化估计值，消除系统随机噪声，提高交通流的实时预测精度。

1 短时交通流不确定性

1.1 不确定性概述

交通流存在复杂的变化规律。虽然在同一区域内，人们的出行方式在时间周期上呈现出一定的规律性，但是随着时间尺度缩短，交通流还表现出时变性、随机性、内在约定性等不稳定特性。交通流复杂性与受到的影响因素密切相关，因此可以从影响交通流的主要因素(人、车、路以及环境等)进行分析。例如，每个驾驶员的生理、心理以及反应特性千差万别，对于他们来说，在下一刻面临的驾驶环境也是不确定的，而前车的运行状态也会直接影响到他们的驾驶情况。并且，不同的路网密度、道路结构、天气情况等在交通系统中也会产生不确定性变化。从以上分析可以看出，影响交通流的各个因素均存在着不确定性，而决定路上交通状态的往往均为多种因素相互作用的结果。驾驶员于何时何地以何种方式和状态进入路网是不可预知的；进入路网后，车辆的运行状态又将受到道路拥挤程度、道路紧急情况等多种因素的影响，这些因素的变化也是不可预知的。这些表现都证明了交通系统中存在很强的不确定性，而这种不确定性集中体现在交通流的变化中，即为交通流不确定性[23]。

1.2 不确定性识别

通过主成分分析法[24](PCA,principle components analysis)可以挖掘短时交通流的内在构成。主成分分析法通过协方差矩阵转换成新的正交坐标系来表征P维空间中与主成分的偏差，偏差可绘制得到主分量谱图。具体分析步骤如下：

步骤1：若已知时间序列{x1,x2,…,xN}，采用时间间隔τ和嵌入维数m，计算轨线矩阵Xl×m如式(1):

(1)

式中：l=N-(m-1)。

步骤2：计算协方差矩阵，方法如式(2)：

(2)

步骤3：得到特征向量Ui(i=1,2,…,m)以及特征值λi(i=1,2,…,m)，并将特征值按照从大到小的顺序排列：λ1≥λ2≥…≥λm，特征值λi和特征向量Ui称为主分量。

步骤4：计算所有特征值之和γ，如式(3)：

(3)

步骤5：以指标i为X轴、ln(λi/γ)为Y轴，绘制主分量谱图。通过主分量谱可以观察到主分量分布之间存在的差异。以桂林市某道路的交通流量数据为例，运用主成分分析法，嵌入维数m依次取4、6、8、10，将分析结果绘制成主分量谱图，如图1。

由图1可以看出，短时交通流的主分量谱倾斜，具有混沌特性，同时存在随机噪声，并且随着嵌入维数增加，水平段越长，噪声越明显。通过分析，可以将交通流的不确定性从随机性和混沌特性两个角度进行描述。总的来说，交通流存在以下特点：一种是交通系统中的规律性，其决定交通流的总体趋势；另一种是不确定性，能够影响交通流实时流量，使得交通流发生扰动。内部不确定性短期内按规律演化，其随着时间增加变为无法估计的内在不确定性，即混沌特性。外部不确定性无法预测，是系统本身客观存在的，具有随机性，即随机噪声。因此，可以把短时交通流看作一组包含随机干扰信号的不确定性时间序列。

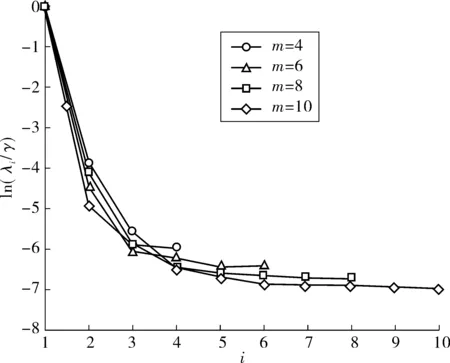
图1 主分量谱Fig.1 Spectrogram of principal component

2 自适应实时预测模型

通过1.2节的分析可知，短时交通流存在不确定性，容易受到未知扰动影响，使得实际交通流在一定范围内呈现大小不一的波动。另一方面，短时交通流又有较强的关联性，与本路段和上下游路段待测时刻前的交通量密切相关[25]。针对此特点，笔者首先利用本路段和上下游路段相关交通数据，通过带遗忘因子的极限学习机建立符合本路段规律的时序模型，使得预测具备充分的可靠程度，而后结合粒子滤波得到最优的预测交通量短时变化估计值，消除随机噪声对预测精度的影响，形成一种自适应实时预测模型。

2.1 带遗忘因子的极限学习机

给定N个不同的训练样本(xi,yi)，xi=(xi1,xi2,…,xin)T∈Rn，yi=(yi1,yi2,…,yim)∈Rm，i=1,2,…,N，隐藏层节点个数为L，激活函数为g(x)，极限学习机(ELM,extreme learning machine)模型如式(4)：

(4)

式中：ωj为隐藏层以及输入层节点间权值向量，ωj=(ωj1,ωj2,…,ωjn)T，其中j=1,2,…,L；βj=(βj1,βj2,…,βjm)T为输出层以及隐藏层节点间权值向量；bj为隐藏层节点偏置。ELM可以表示为矩阵形式：

Hβ=Y

(5)

计算初始隐藏输出矩阵H0，希望求得使满足‖H0β-Y0‖最小的β(0)。根据广义逆的计算方法，可以计算出β(0)：

(6)

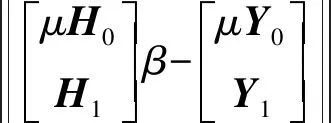
(7)

(8)

对于在线学习，把β(1)表示成β(0)、K1、H1和Y1的函数，即：

(9)

(10)

由此，可得到带遗忘因子的在线序列极限学习机模型的一般形式为：

(11)

(12)

2.2 粒子滤波

通过带遗忘因子的在线序列极限学习机模型可以构建出一个连续的非线性时间系统。在此基础上，可以假设该系统的状态方程和观测方程分别如式(13)、式(14)，进而利用粒子滤波来修正带遗忘因子的极限学习机模型。

xk=f(xk-1,vk-1)

(13)

yk=hk(xk,uk)

(14)

式中：xk为系统在k时刻所产生的交通流；yk为k时刻的观测交通流；fk:Anx×Anv→Anx为状态方程；hk:Anx×Anu→Any为观测方程；vk为过程噪声；uk为观测噪声，假设vk和uk是互不相关、零均值白噪声。

在m阶马尔科夫假设下，根据y1:k递推估计后验概率密度p(x0:k|y1:k)。其中：x0:k={x0,…,xk}为k时刻系统所产生的交通流序列；y1:k={y1,…,yk}为观测交通流序列。

(15)

求得状态变量x0:k的后验概率分布p(x0:k|y1:k)后，根据蒙特卡洛原理，任意函数g(x0:k)的数学期望都可以表示为：

(16)

为了解决从后验概率分布抽取样本比较困难的问题，引入重要性采样方法(importance sampling method)。该方法采用一种重要性采样密度q(x0:k|y1:k)抽取样本来近似p(x0:k|y1:k)，式(15)可以写成式(17)：

E[g(x0:k)]=Eq(·)[g(x0:k)ω*(x0:k)]

(17)

从重要性采样密度q(x0:k|y1:k)中采样后，数学期望可以近似表达为：

(18)

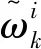
(19)

将重要性采用密度分解为：

q(x0:k|y1:k)=q(xk|xk-m:k-1,yk)q(x0:k-1|y1:k-1)

(20)

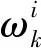
(21)

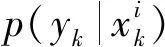
(22)

样本从重要性函数产生，存在偏差。经过若干次迭代后，粒子权值的方差会越来越大，出现退化现象。为了解决此问题，引入有效粒子数Neff衡量算法的退化程度，据此决定何时进行重抽样Neff定义为：

(23)

综上所述，粒子滤波的框架结构如图2。

图2 粒子滤波的框架结果Fig.2 Frame results of particle filter

3 算例分析

以桂林市内的某主干道路段为研究对象进行实验，选取2019年4月一个方向的6个路段固定检测装置获取的交通流时间序列作为数据样本。笔者根据一定算法及预测模型构建的要求，对地图匹配后的数据展开有效程度的评价以及预处理，同时围绕交通流进行求解。在数据具备充分可靠特征的前提下，最终得到连续5天共455个时间点的数据，其中选取交通流数据中前4天的数据作为训练集，选取最后一天的数据为测试集进行实验。

为了验证算法的有效性，选取在线序列极限学习机、带遗忘因子的极限学习机等两种在线学习模型以及比较常用的时间序列(ARIMA)、支持向量机(SVM)和长短期记忆神经网络(LSTM) 3种离线算法模型进行对比分析。对于在线序列极限学习机模型，极限学习机的内部节点数设为10，数据流里每次截取20个时刻点数据输进去在线学习；对于带遗忘因子的极限学习机模型，设置遗忘因子为0.9；对于自适应实时预测模型，增加粒子滤波过程，将转移噪声协方差和测量噪声协方差设置为1，粒子数设为100。

通过MATLAB 2018a对几种模型进行编程求解，并将各模型的预测结果与真实值进行对比，结果如图3。

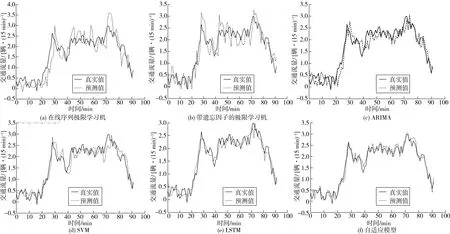
图3 不同模型预测值与真实值的对比结果Fig.3 Comparison results of the predicted values and real values of different models

为了进一步量化各模型预测的整体效果，对平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)4种误差指标进行计算，如式(24)～式(27)。6种预测算法误差指标数据对比结果如表1。

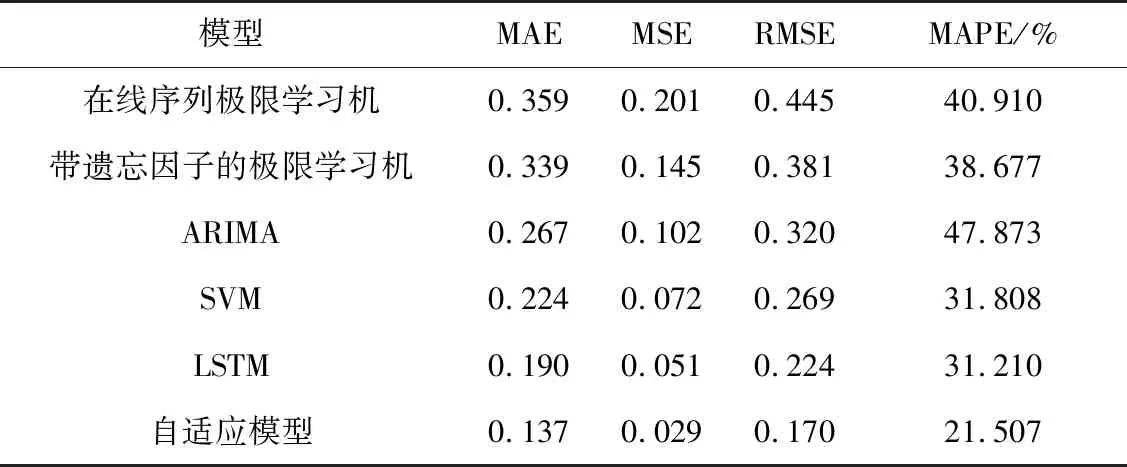
表1 6种预测算法误差指标对比Table 1 Comparison of error indexes of the six prediction algorithms

(24)

(25)

(26)

(27)

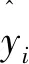
同时，绘制3种在线学习方法在学习过程中的均方误差时间序列分布情况，如图4。

图4 均方误差随时间序列的分布Fig.4 Distribution of mean square error changing with time series

从图3和表1可以看出，传统在线序列极限学习机和带遗忘因子的极限学习机模型的预测精度低于其他3种离线算法模型。虽然传统在线学习方法模型的动态更新可以增加对数据不确定性的适应性，但也存在有风险。在线学习方法在训练一个数据点后直接更新权值，但是更新权值存在不确定性。若存在错误的更新，模型可能会逐渐走向错误的方向，导致预测精度下降。

从图4可以看出，在线序列极限学习机和带遗忘因子的极限学习机训练集绝对误差的变化维度为0～120。带遗忘因子的极限学习机考虑了早期采集数据对预测精度的影响，在一定程度上提高了预测精度，但是依然对突发情况下的交通流变化不够敏感。在线序列极限学习机和带遗忘因子的极限学习机更倾向于交通流的整体变化趋势。而笔者提出的自适应模型均方误差变化维度下降至0～2.5，该模型能很好地应对交通流不确定性的影响。

自适应模型在传统在线学习模型的权值更新上进行了改进，通过粒子滤波的优化效果增加了模型的鲁棒性和可靠性。研究结果表明，笔者提出的自适应模型在对平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)等4种指标上均优于其他预测方法，在路段整体的交通流拟合情况及具体的预测精度上均得到有效提高。

4 结 语

笔者考虑交通流不确定性问题，提出了一种基于遗忘因子和粒子滤波极限学习机自适应交通流实时预测模型。该模型分为两步：首先通过引入遗忘因子(FFOS-ELM)实时修正系统模型参数，解决交通流时变性对预测精度的影响；然后运用粒子滤波(PF)的系统状态最优估计与预测能力，降低交通量 “噪声”，最终形成最优预测。随后笔者使用实测数据对模型展开验证。验证结果显示：应用笔者提出的模型进行短时交通流预测，在预测过程中交通流具有的非线性、模糊性以及随机性等问题对预测结果的影响程度均得到了有效缓解，且在经过整体性处理之后由噪声导致的误差明显降低；模型预测精度优于在线序列极限学习机、带遗忘因子的极限学习机在线学习模型和时间序列(ARIMA)、支持向量机(SVM)和长短期记忆神经网络(LSTM)等离线算法模型，且在路段整体的交通流拟合情况及具体的预测精度上均得到有效提高。