基于改进RRT算法的垃圾收集车路径规划研究

顾海蛟， 宋 宇

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

随着现代技术的发展，无人化时代已然来临，原本需要人工才能完成的简单和危险的工作被机器所代替，比如现在快递业的无人寄取、大疆科技的无人机，以及常见的无人售货机等。就无人驾驶的垃圾回收车而言，决定其性能优劣的实质是内部的动力驱动系统和外部的路径规划问题。其中路径规划问题直接决定着工作效率和是否能够完成所要执行任务的关键。因此，一种合理与高效的路径规划算法是实现其工作性能最大化的保证。

常用的路径规划算法有图搜索法、人工势场法、遗传算法、RRT算法等。图搜索法是在已知环境和障碍物信息构造从起点到目标点的可行路径[1]，主要分为深度优先和广度优先两个方向。在Prim和Dijkstar最短路径算法中采用了广度优先的思想，但规划效果对启发式函数依赖性太强，较好的启发函数需要靠试凑来获得[2]。人工势场法是将整体抽象成一个引力场，目标点对移动物体产生“引力”，障碍物对移动物体产生“斥力”，最后通过“合力”控制物体的运动方向，但规划效果得到的往往不是全局最优路径[3]。遗传算法是一种仿生物算法，随着一代又一代的“遗传”,逐渐找到最优路径，容易出现过早的收敛和停滞现象。RRT算法是一种增量式采样的搜索方法，在应用中不需要任何参数，具备良好的使用性能，它利用增量递增方法构建搜索树，逐渐提高分辨能力，而无需设置任何参数与函数。

文中主要对垃圾回收车的路径规划进行研究，假设在高档小区每个家庭的垃圾都在对应规定的地方投放，而无人回收垃圾车在预先标记的垃圾点自主地将垃圾收集到一起处理，就会考虑到小车路径规划问题，只要将小车路径规划好，效率就会大大提高。在路径规划算法中,RRT算法在应用中需要参数少，具有良好的使用功能，容易实现。借鉴改进RRT算法的基础上，提出一种新的、易于实现的改进RRT算法的路径规划方法。传统RRT算法在设定好出发点和目标点的位置后，只需要在一定的迭代次数后就会找到一条从出发点到目标点的路径，但速度会比较慢，而在改进后的双向随机搜索树是从起始点和目标点并行生成两棵RRT树，直至两棵树相遇，这样会缩短搜索过程用时，减少计算机的计算用时，但会在规划的路径中出现障碍盲区，在实际允许的情形下加入“改线”机制，改进后的算法缩短了路径长度，达到节省能耗的目的。

1 RRT算法概述

RRT算法是一种基于随机采样的树结构搜索算法，以空间给定的起点qstart出发，通过在给定的封闭空间中随机采样,并且引导搜索树的生长。当树的节点进入目标区域内,并且找到终点qgoal时算法结束，然后回溯到起始节点,即可得到所规划的路径。用有向图表示路径G=(u,E)，一条规划的路径就是一系列坐标点的顺序连接(u1,u2,u3,…,un)，u1=qstart,un=qgoal。同时(ui,ui+1)∈E,1≤i≤n-1表示边。实质就是使用采样点来扩展图G，之后就是一条从起点到终点的路径。

RRT算法流程如下：

1.U←{qstart}，E←φ，i←0

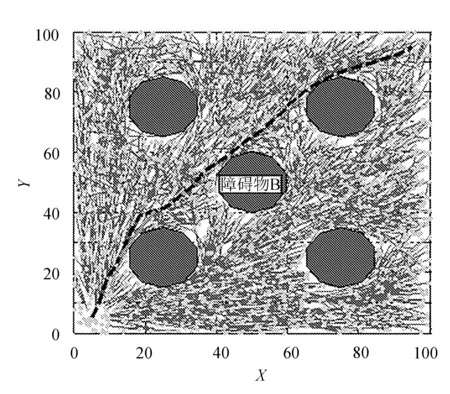
2.While i

3.G′←(u,E)

4.qrand←Sample(i)，i←i+1

5.(U,E)←extend(G′,qrand)

6.G←(G′,qrand)

7.end while

RRT算法的简易图解如图1所示。

图1 RRT算法的简易图解

最初，扩展图G的坐标点集只有初始节点qstart，边集E为空集。然后进入迭代,即进入While循环，迭代次数为N，设置为新的扩展图G′，Sample(i)用来采样一个新的点qrand，利用新的点来拓展图G，最后到达目标点qgoal，结束循环，此时,通过RRT算法找到从出发点到目标点的规划路径[4-7]。

2 RRT-Connect算法概述

RRT-Connect算法是在RRT算法的基础上加上了双树双向抖索的引导策略，并且在扩展路径的方式基础上加入了贪婪策略,用来加快搜索速度。

RRT-Connect算法的简易图解如图2所示。

图2 RRT-Connect算法的简易图解

图2中RRT-Connect算法在搜索路径时，从起始点与目标点两端同时进行路径的搜索，直到两段路径相遇，即全局搜索路径结束，得到规划路径轨迹。

3 算法”改线“机制

经过RRT-Connect算法规划得到的路线将会在障碍物的边缘出现障碍盲区，这一部分盲区主要是由起始点与目标点之间进行双向的树形搜索存在的不足引起的，不能同时兼顾搜索时间短与路径长度短的优点，针对上述问题引入”改线机制“，其原理是三角形的三边原理，如图3所示。

图3 三角形三边原理

假设三角形的三条边长度分别为a，b，c，其中a，b两边的夹角为α，其对应的边为c。三角形两边之和大于第三边，a+b>c。文中就是利用这一原理，在规划的路径中引入改线机制，使得规划后的路径实际运动距离更短。

4 仿真实验

仿真是在Matlab2014上进行的，在采样点给定次数4 000次进行的实验。

起点坐标(5，5)，终点坐标(95，95)通过RRT-Connect算法找到路径。

采样次数2 000次时，部分采样点下生成的路径规划如图4所示。

图4 部分采样点生成路径规划

采样次数4 000次时，全部采样点下生成的路径规划如图5所示。

图5 全部采样点生成路径规划

全部采样点生成的路径长度比部分采样点生成的路径长度少4.25%。

4.1 改线仿真实验

在控制其它变量不变，只改变采样点数的情况下进行仿真实验，下面将进行改线，其中改线是在图5障碍盲区的路径段进行改线，改线后在满足垃圾收集车实际运动轨迹的情形下路径规划如图6所示。

图6 改线后的路径规划

图6相较于图5，生成的路径长度减少4.45%。

4.2 仿真数据对比

算法结果对比见表1。

表1 算法结果对比

改进后的算法路径在保证采样点数，运行时间一样的情况下长度减少了。达到了减少实际运行路径长度的目的。

5 结 语

提出的基于改进RRT-Connect算法的垃圾收集车路径规划算法，通过利用三角形三边定理进行“改线”，得出的实际运行路径长度相较于原始算法更短，能达到减少耗能的目的。仿真结果表明，改进后的算法路径长度相较于原始算法的路径长度缩短了4.45%，有很大的利用价值。