危险品公铁联运模糊多目标路径优化研究
孙 岩,虞 楠,董坤祥
(1.山东财经大学管理科学与工程学院,济南 250014;2.交通运输部水运科学研究院,北京 100088)
目前,危险品运输仍以公路运输为主,但运输事故频发.相较于公路运输,铁路运输在长距离运输方面具有经济性好、可靠性强的优势,因而更适合危险品长途运输.此外,充分发挥公路运输在中短途货物集散上机动灵活的优势可实现危险品“门到门”运输.因此,危险品公铁(公路铁路联运)在世界各国的运输实践中得到了大力推广.危险品公铁联运路径规划通过整合两种运输方式,规划合理的运输路径,有效控制和降低危险品运输风险[1].
目前,关于危险品运输路径优化的文献大都集中在危险品车辆路径问题(Vehicle Routing Problem)[2-5]或者基于车辆路径问题的“选址—路径”优化(Location-Routing Problem)[6-8].而针对危险品公铁(多式)联运路径优化的文献相对较少.较车辆路径问题,公铁(多式)联运路径规划问题更为复杂.一方面,公铁(多式)联运路径规划需要首先确定运输网络结构形态,常见的网络结构包括点对点网络(Point-to-Point Network)、轴辐式网络(Hub-and-Spoke Network)以及集散网络(Collection-and-Distribution Network)等[9].另一方面,较车辆路径规划只考虑单一运输方式,公铁(多式)联运路径规需要协调不同运输方式以构建完整的运输链条,不同运输方式运输组织模式的不同增加了路径规划的难度[10].因此,危险品车辆路径问题的优化模型难以直接应用于危险品公铁(多式)联运路径规划上.
运输规划领域的学者对危险品公铁(多式)联运路径规划问题进行了研究:辛春林等[11]研究了时变条件下危险品多式联运最短路模型和改进的Dijkstra算法;曹欢等[12]基于条件风险价值理论,构建了考虑风险规避程度的危险品公铁联运路径选择模型;黄丽霞和帅斌[13]以总成本和总风险最小为目标,构建了危险品多式联运路径双目标整数线性规划模型,设计了寻找非劣路径的路径搜索算法;Verma等[14-15]研究了考虑运输时限约束的危险品公铁联运规划问题,给出了基于高斯烟羽模型(Gaussian Plume Model)的暴露人口数计算方法;Xie等[16]以及Ghaderi&Burdett[17]分别研究了危险公铁(多式)联运的选址—路径规划问题,其中,选址的目的在于选择合适的中转节点进行不同运输方式之间的中转,且选址—路径优化的规划周期要长于路径优化;Assadipour等[18]以及Mohammadi等[19]学者还对危险品公铁(多式)联运网络设计问题(Network Design Problem)进行了研究.与路径规划相比,危险品公铁(多式)联运网络设计为长期规划,且在规划时大都只考虑运输起讫点之间的长期运量,而路径规划问题则关注具体的运输订单.
以往文献在危险品公铁(多式)联运路径规划问题上取得了一定的进展,在运输可靠性上均研究了确定环境下的危险品公铁(多式)联运路径规划问题,但在实际决策中,决策者需要根据危险品运输订单的具体要求提前规划运输路径.公路运输时间由于受到公路拥堵、交通事故、恶劣天气等若干原因的影响,具有明显不确定性[9].考虑到公铁中转作业受到铁路货运列车固定作业时间窗的限制,若采用确定规划,过高估计公路运输时间可能会导致危险品过早到达铁路货运站,造成作业等待时间延长和相应存储费用的增加;而过低估计运输时间则会导致危险品延迟到达,一旦晚于列车作业停止时刻,会无法完成中转作业,导致路径规划失败.同时,由于客户运输时限的约束,公路运输时间的不确定性也会影响危险品配送至客户的时效性.因此,规划不确定公路运输时间是提高危险品公铁联运路径优化可靠性及时效性的关键.
在运输系统规划上,一方面,以往文献规划的危险品公铁(多式)联运网络结构与运输实践中广泛应用的轴辐式网络相差较远,另一方面,危险品公铁联运系统中的公路运输与铁路运输采用的是截然不同的运输组织模式.前者组织运输在时间上是灵活自由的,而后者则需要按照固定的列车开行方案进行组织运输.以往这方面的研究在规划危险品公铁联运路径时忽略了列车开行方案对路径规划在时间和空间上的限制.
针对以往研究的不足,本文首先对轴辐式公铁联运系统进行分析,并对列车开行方案约束以及危险品运输风险进行了规划,然后从模糊规划的角度出发,采用梯形模糊数(Trapezoidal Fuzzy Numbers)对公路运输时间的不确定性进行了建模.据此,在参考作者以往优化建模[9,20]的基础上,构建了危险品公铁联运路径优化的模糊多目标线性规划模型,并分别采用模糊期望值法(Fuzzy Expected Value Method)和模糊排序法(Fuzzy Ranking Method)对模糊目标和模糊约束进行清晰化处理,得到清晰的多目标线性规划模型.清晰化模型的帕累托解可采用标准化加权求和法(Normalized Weighting Method)获得.最后,进行算例研究,验证了上述方法的有效性,并采用敏感性分析法对算例优化结果进行了讨论.
1 危险品轴辐式公铁联运系统规划
危险品公铁联运综合运用基于列车开行方案的铁路运输和灵活组织的公路运输,实现危险品的“门到门”运输.在各类公铁联运模式中,“公路中短途集运—铁路长途运输—公路中短途疏运”模式充分利用了公路运输在中短途货物集散上机动灵活的优势,以及铁路运输在长途运输中经济性好、可靠性强的优势.如图1所示,基于该运输模式的轴辐式网络被广泛认为是最适用于公铁联运系统的结构[9,20].因此,本文将对轴辐式公铁联运系统进行建模.在公铁联运轴辐式网络中,铁路货运列车的装车组织站和卸车组织站是网络的枢纽节点(Hub),通过货物集疏运可在枢纽节点形成规模经济;运输的起点和终点是网络的非枢纽节点(Spoke).装车组织站和卸车组织站之间开行具有固定周期的铁路货运列车,运输起点与装车组织站以及卸车组织站与运输终点依靠公路运输连接.对于公路联运网络中的铁路货运列车,不同开行周期内的同一列车将作为不同的铁路运输服务予以不同的标号,从而降低优化模型中相关参数和变量的维度,起到简化模型的作用.

图1 轴辐式公铁联运网络Fig.1 Hub-and-spoke road-rail multimodal network
在公铁联运中,铁路运输需要根据事先规划好的列车开行方案进行组织.列车开行方案规定了铁路货运列车在装车组织站的固定出发时刻,在装车组织站和卸车组织站的服务时间窗、卸车组织站的到站时刻、开行频率和开行路径[21].在进行公铁联运时,所规划的路径应满足列车开行方案对危险品中转作业的如下约束:
1)在装车组织站进行中转作业时,危险品经由公路运输到达装车组织站并完成卸车的时刻间不应晚于后续铁路货运列车装车作业时间窗的上界(装车作业停止时刻),否则无法进行中转作业.但是该时刻可以早于该时间窗的下界(装车作业开始时刻),此时危险品需要等待至装车作业开始时刻,然后完成装车作业.
2)当在装车组织站完成装车后,危险品需等待至列车的固定出发时间,然后随列车运往卸车组织站.到达卸车组织站后,危险品需要等待至该列车在卸车组织站卸车时间窗的下界(卸车作业开始时刻),然后进行卸车作业.
考虑到公路运输组织的自由灵活,公路集疏运作业可按如下流程规划:装载危险品的公路货运卡车在运输开始时刻从运输起点出发,将危险品运抵装车组织站并完成卸车作业;在卸车组织站,当铁路车辆在货场完成危险品卸车后,公路货运卡车可即刻进行危险品装车作业,并在装车作业结束后即刻进行危险品疏运,将危险品运抵运输终点.
由图1所示,轴辐式公铁联运网络以及网络中的危险品运输路径均由节点和弧段构成.危险品运输事故既有可能发生在运输途中(弧段上),也有可能发生在中转过程中(节点上).因此,危险品运输风险同时存在于公铁联运网络的节点与弧段上[21].在危险品运输规划研究中,“暴露人口吨数”,即危险品运量与发生危险品运输事故时影响的人口数量的乘积[13],是最常用的运输风险指标.对于危险品公铁联运,将运输风险按照运输路径上节点和弧段的累积暴露人口吨数进行建模.
2 优化建模
2.1 不确定公路运输时间的模糊规划建模
随机规划和模糊规划均可用于不确定问题的优化求解.随机规划对不确定参数进行概率分布拟合需要依赖大量历史数据,但是在规划阶段,往往难以获取足量的数据.因此,随机规划处理实际问题的可行性有限[9,22].根据模糊集理论的原理,结合专家经验和有限的历史数据,采用模糊数对公路运输时间的不确定性进行刻画,并据此采用模糊规划对危险品公铁联运路径规划问题进研究.
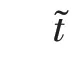

图2 不确定公路运输时间的梯形模糊数表示Fig.2 Uncertain road transportation time represented by a trapezoidal fuzzy number
2.2 符号及定义
2.2.1 运输订单 以K表述危险品运输订单集合.对于任一运输订单k∈K,ok和dk分别表示运输起点和运输终点;t0k表示运输开始时刻;φk表示运输订单k运输时限;qk表示运输订单k中危险品的需求量(t).

2.3 模糊多目标混合整数线性规划模型
2.3.1 目标函数 目标函数(1)表示危险品公铁联运路径优化的经济目标,即完成所有危险品运输订单的费用最小化.其中,费用包括危险品在途运输费用、节点中转作业费用和节点存储费用.
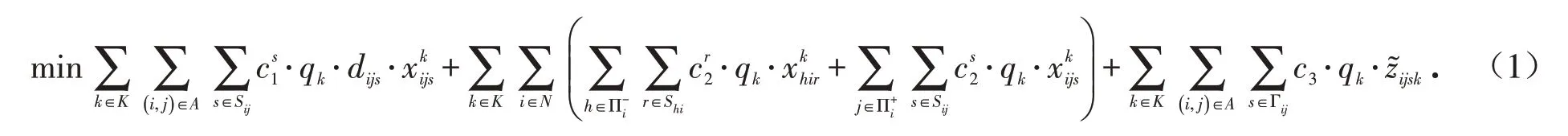
目标函数(2)表示危险品公铁联运路径优化的风险目标,即所有公铁联运路径节点及弧段上的累积暴露人口吨数最小化.

2.3.2 约束条件 约束条件(3)和约束条件(4)分别为流量平衡约束和危险品运输订单的完整性约束.两者共同保证任一运输订单中的危险品需求量是不可拆分的.
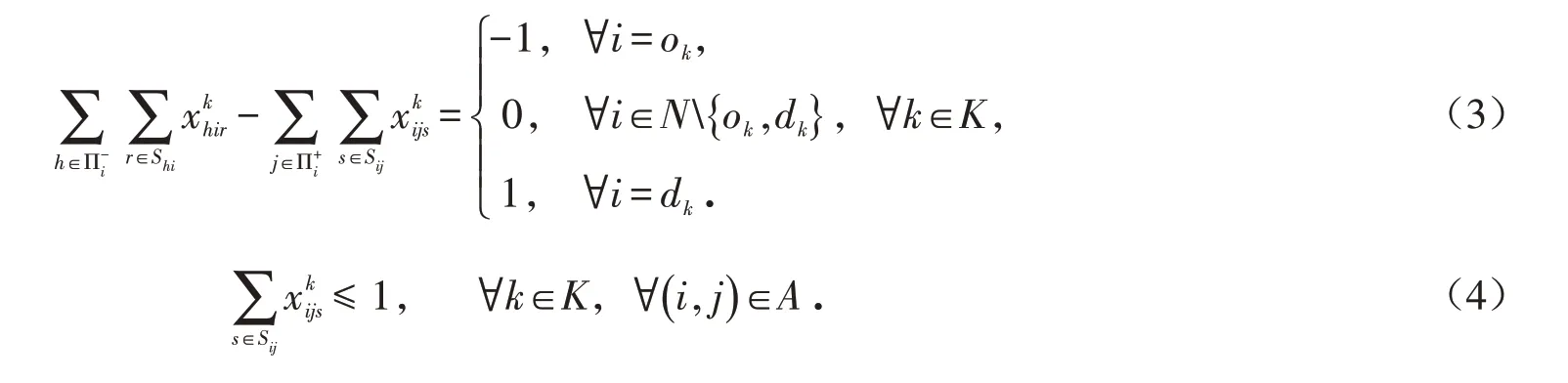
假设危险品在其运输订单规定的运输开始时刻准时进行装车作业.约束条件(5)和(6)根据模糊运算法则计算了公铁联运公路集运过程中危险品由公路运输运抵铁路装车组织站的时刻.
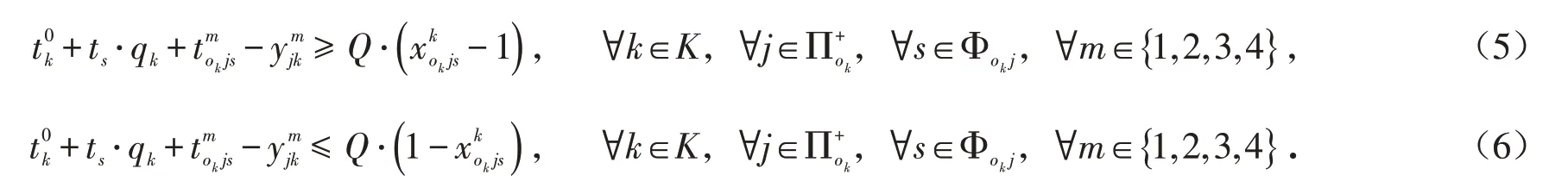
约束条件(7)和(8)根据模糊运算法则计算了公铁联运公路疏运过程中危险品由铁路卸车组织站经公路运输到达运输终点的时刻.
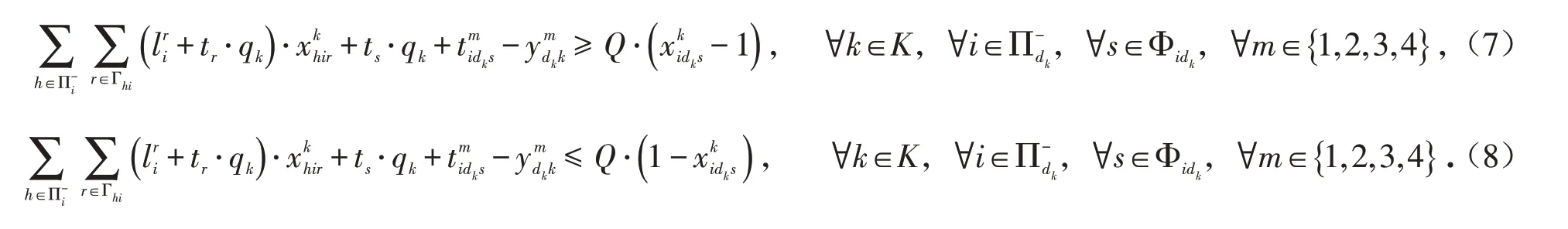
约束条件(9)和(10)根据模糊运算法则计算了危险品在装车组织站等待装车作业而产生的存储时间.
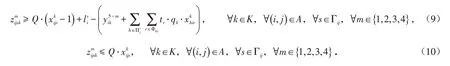
约束条件(11)为运输服务能力约束,保证所分配运输订单的危险品需求量之和不超过弧段上所选运输服务的运输能力.

约束条件(12)为铁路货运列车装车作业时间窗约束,保证危险品到达装车组织站并完成中转作业的时刻不晚于后续所选铁路货运列车在该节点作业时间窗的上界.
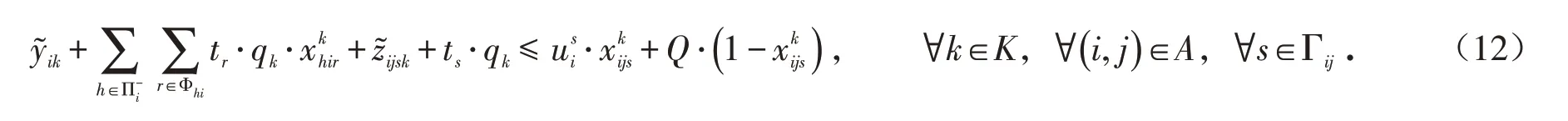
约束条件(13)为危险品运输订单的运输时限约束,保证危险品到运输终点并完成卸车的时刻(运输订单完成时刻)不晚于客户要求的运输时限.
约束条件(14)~(18)为确定变量和模糊变量的取值约束.
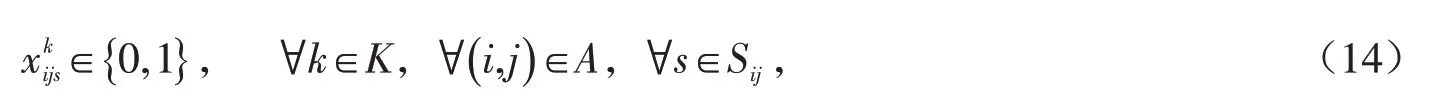

3 求解方法

因此,目标函数(1)的清晰化形式如式(20)所示:
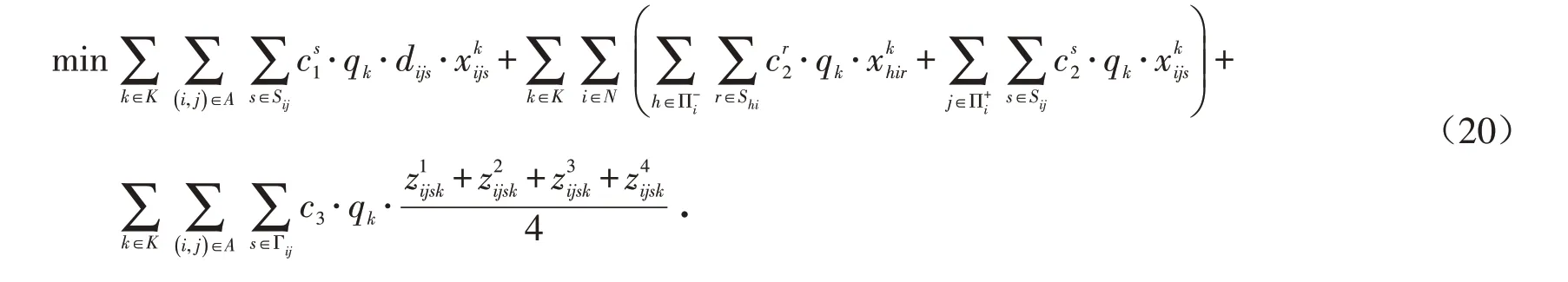
模糊期望值法可以用于模糊不等式约束的去模糊化,但是会降低问题优化的灵活性[22].本文采用Jimenez模糊排序法[23-24]对模糊不等式约束(12)和(13)进行清晰化处理.根据模糊排序法,不等式约束(12)和(13)的清晰化形式如式(21)和(22)所示.

式(21)和(22)中,参数λ、θ∈[0,1]表示模糊不等式约束所代表的模糊事件成立的最小置信度,其取值由决策者根据主观意愿而设定;λ可视为规划路径满足列车开行方案约束的可靠性,而θ可视为规划路径满足客户运输时限要求的时效性,两者反映了决策者在运输可靠性和时效性上的偏好,理论上,两者取值越大,规划路径的可靠性和时效性越高.与广泛应用的模糊机会约束规划法(Fuzzy Chance-Constrained Programming Method)相比,模糊排序法既不会增加约束的个数,也保证了模型的线性性,从而有利于模型的求解[23].
经过清晰化处理,如2.3节所示的模糊规划模型可转化为等价的多目标混合整数线性规划模型,目标函数如式(2)和(18)所示,约束条件包括式(3)~(11)、式(14)~(16)及式(21)和(22).本文采用标准化加权求和法[20],将经济目标和风险目标分别除以各自的最优解以实现优化目标的标准化从而消除量级和单位的影响,然后对标准化后的目标进行加权求和,将其作为单目标混合整数线性规划模型的优化目标,最后通过不断调节目标权重,求解不同权重下的模型,得到问题的帕累托解.
4 算例研究
参考文献[23]中的算例设计对图3所示的轴辐式公铁联运网络中的危险品运输路径进行优化.公铁联运网络中铁路运输服务及其开行方案、公路运输服务(除模糊运输时间)分别详见文献[23]中附表1和附表2.公铁联运网络中节点和弧段的单位暴露人口数也参考文献[23]进行设定.以小时为单位的模糊公路运输时间在图3中表明,在算例研究中,危险品铁路运输的单位运输费用为0.20元/(t·km),单位装卸作业费用为5.80元/t,单位装卸时间为0.02 h/t,单位存储费用为0.15元/(t·h);危险品公路运输的单位费用为0.75元/(t·km),单位装卸作业费用为5.50元/t,单位装卸时间为0.01 h/t.
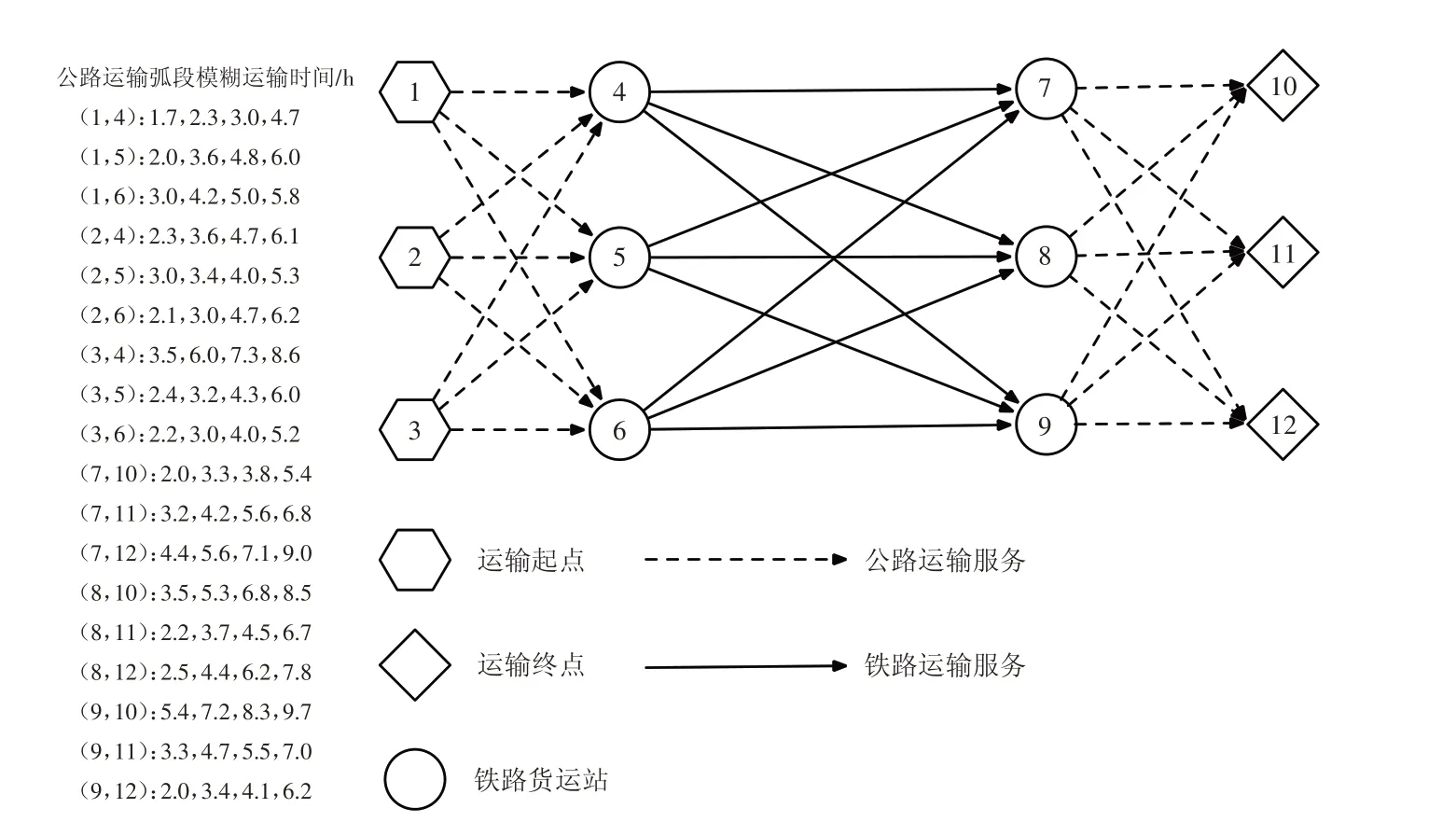
图3 算例中的轴辐式公铁联运网络Fig.3 Hub-and-spoke road-rail network in the numerical case
算例中的运输订单如表1所示.表中危险品运输订单的运输开始时间和运输时限均经过了离散化处理而转化为相应的实数(例如运输订单的运输时限为第二天的23时,经离散化处理后为47).
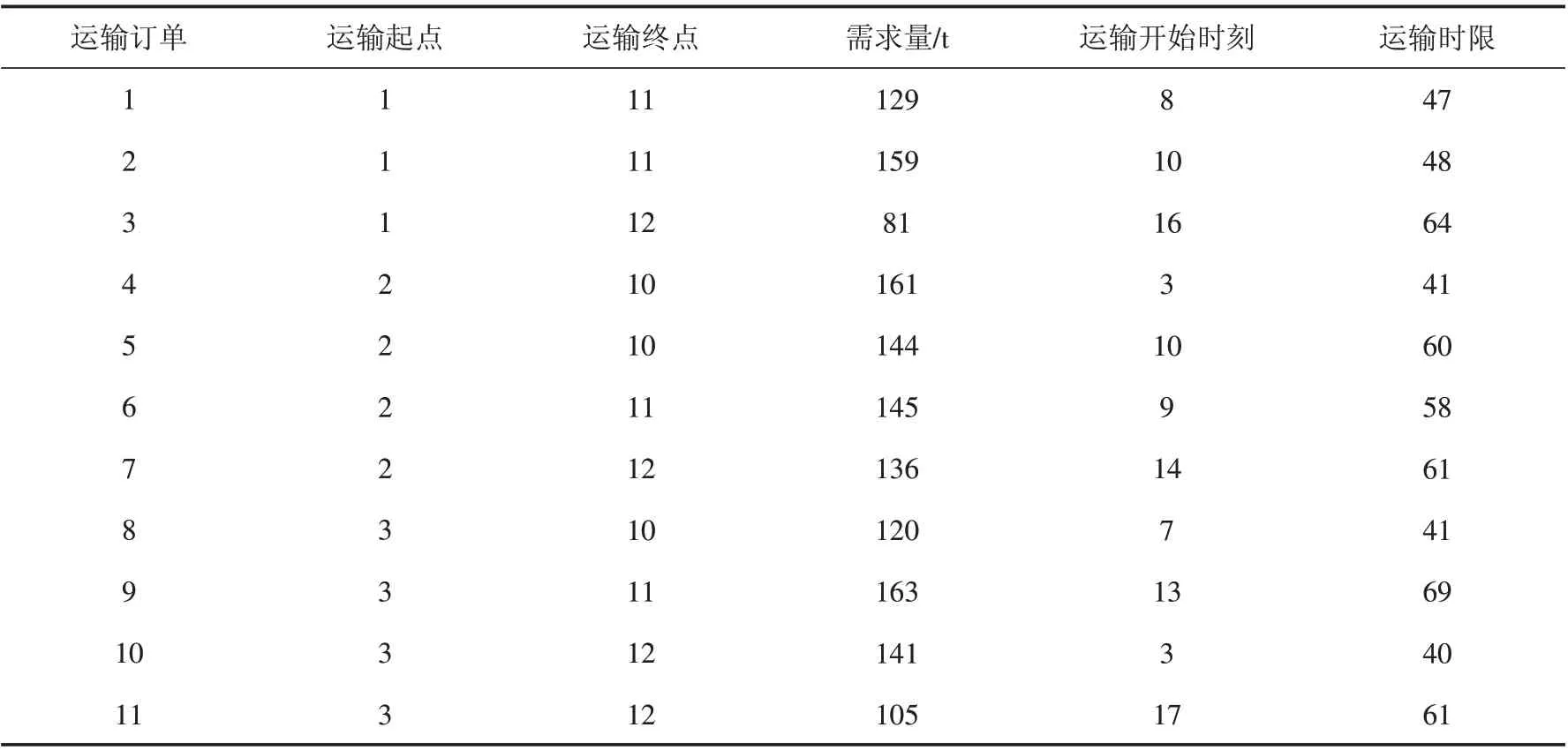
表1 算例中危险品运输订单Tab.1 Information on the hazardous materials transportation order in the numerical case
利用数学规划软件LINGO运行分支定界算法(Branch-and-Bound Algorithm)对危险品公铁联路径规划问题进行优化求解.在求解前,假设决策者对可靠性和时效性的偏好均为0.8(即λ=0.8,θ=0.8).此时,危险品公铁联运算例的帕累托解如图4所示.由图4可知,危险品公路联运路径优化的经济目标和风险目标是互相矛盾的,二者无法同时达到各自的最优值,某一优化目标的改善势必会影响另一优化目标的质量.因此,在规划危险品公铁联运路径时,需要对经济目标和风险目标进行折中处理.图4所示的帕累托解集为进行路径规划提供了多样化的备选方案.
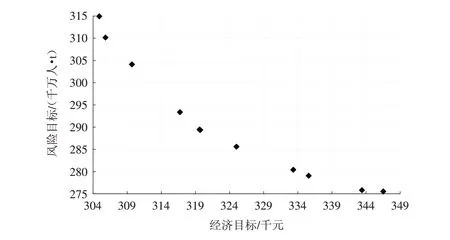
图4 危险品公铁联运路径优化问题的帕累托解Fig.4 Pareto solution to the hazardous materials road-rail multimodal routing problem
决策者的可靠性偏好和时效性偏好往往影响危险品公铁联运路径优化结果.本文采用敏感性分析法分别探讨可靠性偏好和时效性偏好对优化结果的影响.公铁联运路径优化结果包括多个帕累托解,首先假设决策者等同重视经济目标和风险目标,并探讨可靠性偏好和时效性偏好对该决策情境下模型优化结果的影响.此时,标准化加权求和法中两目标的权重均为0.5.将时效性偏好θ设为0.7,分别计算当可靠性偏好λ为0.2、0.4、0.6、0.8和1.0时的路径优化结果,计算结果如图5.
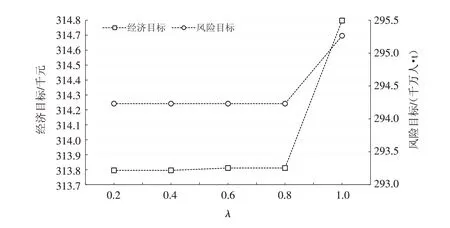
图5 危险品公铁联运路径优化对决策者可靠性偏好的敏感性分析Fig.5 Sensitivity analysis on the hazardous materials road-rail multimodal routing problem with respect to the decision makers’reliability preference
由图5可知,较风险目标,路径规划的经济目标对可靠性偏好的敏感性更明显.当可靠性偏好超过0.8时,路径规划结果对可靠性偏好的敏感性尤为明显.同时,随着决策者对可靠性要求的提高,规划路径的经济目标和风险目标均呈现出增长的趋势,也即提高路径规划的可靠性势必以降低路径规划的经济性、提高路径规划的风险为代价.
为分析决策者时效性偏好对危险品公铁联运路径优化结果的影响,将可靠性偏好λ设为0.7,分别计算当时效性偏好θ为0.2、0.4、0.6、0.8和1.0时的路径优化结果,计算结果如图6.
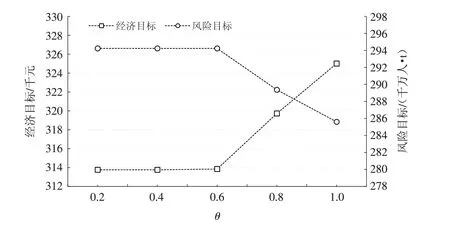
图6 危险品公铁联运路径优化对决策者时效性偏好的敏感性分析Fig.6 Sensitivity analysis on the hazardous materials road-rail multimodal routing problem with respect to the decision makers’timeliness preference
由图6可知,当时效性偏好超过0.6时,路径规划结果对时效性偏好的敏感性尤为明显.同时,随着决策者对时效性要求的提高,规划路径的经济目标呈现出增长的趋势,但是风险目标却呈现出降低的趋势,也即提高路径规划的时效性会同时降低路径规划的风险性,但是需要以降低路径规划的经济性为代价.因此,结合图4~图6可知,危险品公铁联运路径优化需要在经济性、风险性、可靠性和时效性之间进行折中处理,在实际决策中,决策者的可靠性偏好和时效性偏好并非越高越好.决策者可借层次分析法或多属性决策法[25]根据具体决策情境确定合理的可靠性和时效性偏好设计运输方案、组织危险品公铁联运.
5 结语
以轴辐式网络构建了公铁联运系统,规划了列车开行方案对公铁联运路径的约束.基于模糊集理论采用梯形模糊数对不确定公路运输时间进行了建模,以提高了危险品公铁联运路径优化的可靠性和时效性.以“费用—风险”多目标优化为基础,构建了危险品公铁联运路径优化的模糊多目标线性规划模型,并设计了基于模糊期望值法、模糊排序法和标准化加权求和法的求解策略,从而使得决策者可利用数学规划软件运行精确求解算法得到问题的帕累托解.算例研究表明了上述方法的可行性,揭示了危险品运输路径优化的经济目标和风险目标之间的矛盾对立关系,同时分析了决策者可靠性偏好和时效性偏好对危险品公铁联运路径优化的影响.

