基于平均距离聚类的NSGA-II

崔志华 张茂清 常 宇 张江江 王 晖 张文生

近年来,随着复杂工程优化问题的大量出现,多目标优化问题(Multi-objective optimization problems,MOP)逐渐受到许多研究人员的重视.不同于单目标优化问题,多目标优化问题具有高复杂性、非线性和目标函数相互冲突等特点,且不存在全局最优解,而是一个最优解集(Pareto optimal set).

为了有效求解多目标优化问题,学者们引入许多解决方法,如加权和法、目标规划法和极大极小法等.在具有一定先验知识前提下,上述方法可以取得较好结果,但它们通常只能获得一个Pareto 最优解.进化算法的出现为解决多目标优化问题开辟了新思路,利用进化算法并行性、智能性、自适应性和自组织性,多目标进化算法可以计算多个Pareto 最优解[1－3].

多目标问题复杂性主要体现在目标函数个数上,因此,一种较为常见的研究思路是设计高效策略以减少目标函数个数.Yang[4]提出采用随机加权和方法把多个目标函数动态整合为一个单目标函数,通过变化不同权重得到Pareto 最优解集.Zhang等[5]提出的MOEA/D(Multi-objective evolutionary algorithm based on decomposition)算法将多目标优化问题分解为一定数量的单目标优化子问题,然后对这些子问题同步求解.巩敦卫等[6]将高维多目标优化问题分解为若干子优化问题,每一个子优化问题除了包含原优化问题的少数目标函数之外,还将其他目标函数相关信息融合成一个新目标函数,以降低问题求解难度.Schaffer[7]把种群按照目标数量分成若干子种群,在每个子种群中按照个体适应度选择出每个目标上最优个体,然后将这些个体重新组合成种群.丁进良等[8]提出一种基于参考点预测策略的动态多目标优化算法,该算法能快速跟踪动态变化的Pareto 前沿.李文彬等[9]提出一种基于决策空间变换的最近邻预测方法,通过属性趋势模型引入决策空间到目标空间的映射知识,使决策空间的最近邻更有效反映目标空间的最近邻,从而预测多目标优化Pareto 支配解精度[10].

根据无免费午餐定理,每个智能优化算法都只对某些问题有效,因此,利用不同算法优点设计混合策略就成了一种提高算法性能的常见方法[11－14].Zitzler 等[15]利用适应度分配策略、密度估计和增强的存档截断方法设计了SPEA2.Yang 等[16]根据种群进化过程中支配解和非支配解比例大小,把搜索过程分割为三个阶段,并在每个阶段设计了不同搜索策略.徐斌等[17]和Wang 等[18]针对约束多目标优化问题,提出了一种差分进化算法和alpha 约束支配处理的混合优化算法,该算法在初期能有效利用不可行解所携带有用信息,增加种群多样性,在后期则控制不可行解比例,使得算法朝可行域方向进化.陈志旺等[19]将高斯过程和智能进化算法进行结合提出一种融合多属性决策的双层种群筛选策略,并将其嵌入到遗传算法求解高斯模型参数.针对解分布性问题,林浒等[20]以免疫克隆算法为框架,引入适应度共享策略,提出了具有良好分布性的多目标优化进化算法.Tran 等[21]、Pooja 等[22]和Wang等[23]将差分进化算法中交叉算子和人工蜂群算法结合,提出了新的混合多目标进化算法.

针对求解问题特点设计策略,能得到较好满意解[24－26].刘潭等[27]针对单位产油量综合能耗模型输出与实际值存在较大误差的问题,利用高斯混合模型(Gaussian mixture model,GMM)对单位产油量综合能耗混合模型误差特性进行描述,实现对模型的误差补偿,并将误差补偿后的单位产油量综合能耗引入到已建优化模型中,使得优化结果更接近实际最优值.付亚平等[28]针对生产工序的合并造成一种串并联共存的生产布局,建立了混合整数规划模型.针对模型特点,他们设计了一种改进的非支配排序遗传算法,同时采用基于启发式方法的种群初始方式提高种群多样性,并引入一种局域搜索策略以改善算法所获得非支配解及分布性[29－30].乔俊飞等[31]针对污水处理过程控制能耗过大和水质超标严重等问题,通过记忆多目标智能优化算法的动态处理信息,建立环境变量参数与最优解之间的知识模型.利用定向局部区域寻优以及随机全局寻优策略,提高了算法收敛性,获得了更高质量的解[32－33].

NSGA-II[34]是Deb 等在2002 年提出的多目标优化算法,其具有较低计算复杂性且在相同时间内能获得较优的求解性能.为了得到汽车制动器中多目标参数优化问题,张屹等[35]提出了基于正交设计的NSGA-II,得到了分布更优的Pareto 前沿面.为了解决多目标柔性作业车间调度问题,Yuan等[36]把分层策略融入了NSGA-II,提出了混合局部搜索的NSGA-II.路艳雪等[37]尝试把多输入多输出的反向传播(Back-propagation,BP)神经网络和NSGA-II 融合,提高了算法运算速度和计算精度.

为了进一步提升NSGA-II 性能,近年来许多研究者尝试把聚类思想融入该算法中.例如,Mukhopadhyay 等[38]提出将模糊聚类思想应用于NSGA-II,并基于该方法从所求Pareto 前沿面中获得了较优的聚类结果.不同于以往单个标准聚类方法,Handl 等[39]提出两标准的聚类方法,并进一步将其与进化算法结合;与一些单标准聚类算法相比,该改进方法具有较优效果[40－41].类似地,刘丛等[42]利用使用欧氏距离和Path 距离设计出新的聚类框架,并融合多目标进化算法有效提升了算法性能.

上述聚类思想与多目标进化算法融合大多根据已有聚类聚方法进行改进.与以上对NSGA-II 改进不同,本文受聚类思想启发,针对算法多样性方面存在的缺陷[43－44]设计了新的平均距离聚类的多样性指标.基于平均距离聚类多样性指标,整个种群可均匀划分成若干个小种群,并可将NSGA-II 的选择和交叉算子等操作应用在小种群中,从而保证算法所求结果均匀分布在Pareto 前沿面上,称改进后算法为基于平均距离聚类的NSGA-II 算法(NSGA-II with average distance clustering,ADCNSGA-II).

本文组织如下:第1 节介绍多目标优化领域中的基本概念及NSGA-II 基本框架;第2 节详细介绍了基于平均距离聚类的NSGA-II,包括选择和交叉算子的设计;第3 节利用SCH 及ZDT 测试集,将所提算法与常用多目标优化算法进行对比实验,并分析了参数S 对算法性能影响;最后给出了本文结论和未来研究方向.

1 基本NSGA-II 框架

本文考虑如下多目标优化问题:

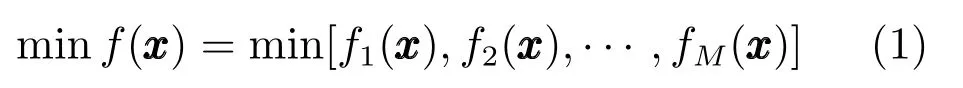
其中,fi(x)表示第i 个目标函数,i=1,2,···,M,x=(x1,x2,···,xD)∈RD为决策变量空间.

定义1.若变量x 的目标函数为f(x)=(f1(x),f2(x),···,fM(x))T,变量x′的目标函数为f(x′)=(f1(x′),f2(x′),···,fM(x′))T,当且仅当对于∀i ∈{1,2,···,M},fi(x)≤fi(x′)成立,且存在k ∈{1,2,···,M},使得fk(x)＜fk(x′)严格成立,则称x 支配x′,记作:x ≺x′.

定义2.决策空间上所有Pareto 最优解构成的集合称为Pareto 最优解集(ParetoSet,PS)

定义3.Pareto 最优解集在目标空间上对应的点集称为Pareto 前沿面(ParetoFront,PF).

NSGA-II[34]主要采用了快速非支配排序(Fast non-dominated sorting)和拥挤度距离(Crowding distance)的概念.快速非支配排序主要思想如下:首先,对种群P 中所有个体计算两个参数,支配个体p 的个体数量(np)和个体p 所支配的个体集合(Sp).对于任意个体p,若np=0,则其被放入第1层非支配前沿面F1.对np=0 的个体,遍历其所支配的个体集合Sp中每一个个体(q)并执行nq-1,此时若nq=0,则放入临时集合Q 中.遍历完F1所有个体的支配集合之后,此时Q 所有个体组成第2 层非支配前沿面F2.重复上述步骤,直到所有个体都被识别出其所在前沿面.

拥挤度距离用于衡量种群多样性,设fk(xi),k=1,2,···,M,i=1,2,···,N 为目标函数,基于每个目标函数值对所有个体进行升序排列,排在第一位(即函数值最小)的个体,其拥挤度距离为d1=∞,排在最后一位(即函数值最大)的个体,其拥挤度距离为dL=∞,其余个体的拥挤度距离按照下式计算:

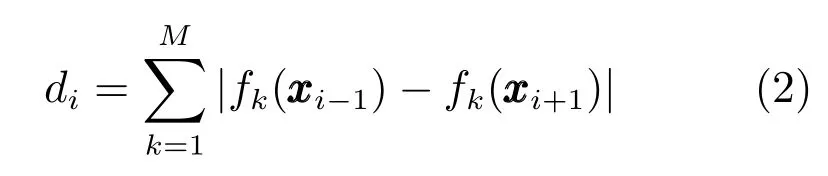
其中,di表示个体xi的拥挤度距离,fk(xi+1)表示个体xi+1的第k 个目标函数.

拥挤度距离计算过程可通过图1 简要说明如下.假设图1 中有A 点、B 点及其相邻的邻居,且A 与B 互不支配.根据式(2),可以得出B 点的拥挤度距离为与B 点相邻的两点的每个函数维度距离之和,即B 点的拥挤度为8l ;同样,可得A 点拥挤度距离为9l .从数值结果上看,B 点比A 点更加拥挤;从图1 可以直观看出A 点比B 点更加拥挤.根据拥挤度距离的定义,算法应该去掉B 点,保留A 点.如果交叉的父代选择了A 点和C 点,由于A和C的距离过近,会导致子代个体与父代A和C 没有明显差异,进而导致算法收敛到某一局部最优解而不能均匀地分布在整个Pareto 前沿面上.这显然不符合我们对拥挤度距离的预期.

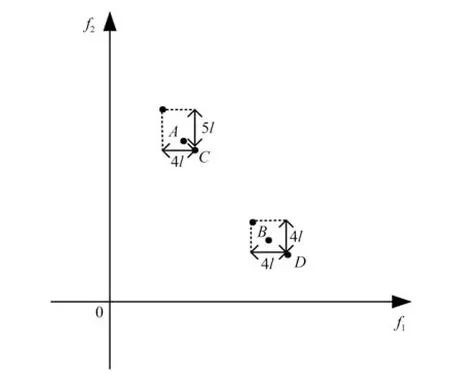
图1 熔化率与比例、积分系数之间的关系Fig.1 Comparing melting rate with proportion and integral parameters of the consarc controller

2 基于平均距离聚类的NSGA-II

为更清楚地介绍基于平均距离聚类的NSGAII,第2.1 节首先介绍匹配选择,然后在第2.2 节中详细介绍平均距离聚类的多样性指标,之后在第2.3节中将其应用于NSGA-II 的选择算子,第2.4 节将其应用于交叉算子,最后总结本文所提算法的基本框架.

2.1 匹配选择

为加快整个种群的收敛速度和保证种群多样性,本文引入了匹配选择操作对种群进行选择.在匹配选择中,本文借鉴SPEA2 赋值方法对种群个体适应值进行重新赋值,该赋值方法不仅考虑种群个体之间的支配关系,也考虑种群个体间的被支配关系(其中种群个体赋值方法可参考SPEA2,不再详细说明).基于以上赋值的适应度值,将非支配个体保存到一个初始为空的一个种群P0中,为防止种群P0大小超出边界,这里采用聚类截断方法使得整个种群大小达到要求的种群大小值N,最后将得到种群作为匹配选择算子的子代输出.具体匹配选择算子的伪代码如下.

算法1.匹配选择算子

2.2 平均距离聚类的多样性指标

平均距离聚类的多样性指标 (Averagedistance-clustering diversity index)主要采用聚类思想,把平均距离内多个个体划分为一个小种群.

假设种群P=(x1,x2,···,xN)有N 个个体,f(xi)=(f1(xi),f2(xi),···,fM(xi))为个体xi的目标函数,则种群P 中第j 个目标函数最大值fj,max和最小值fj,min分别为

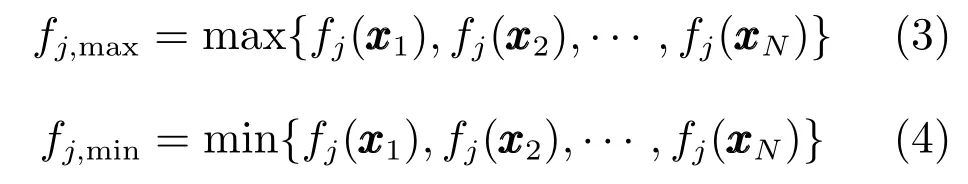
定义群体在第j 个目标函数的平均距离fj,step为

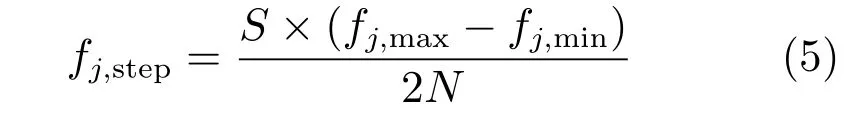
其中,S 表示每个小种群所含个体数量.由于在实际算法运行中,个体之间相对位置具有随机性,因此实际小种群中个体数量需要根据问题的特点设置.

如图2 所示,若在目标空间中有点A、B和C,对应在坐标轴f1上投影分别为A′、B′和C′,且D为A′和B′中间点,E 为B′和C′中间点.若要在f1上形成以B′为中心的小种群,且不能与相邻小种群有交集,则此时B′点所在小种群的选择半径只能为两个相邻点距离一半.

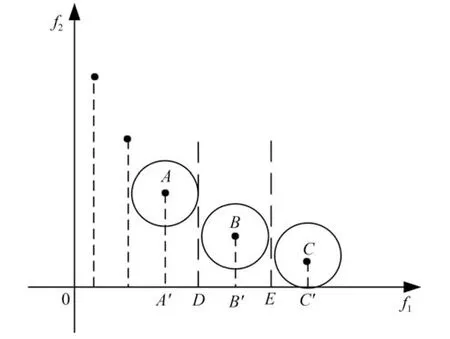
图2 式(5)中参数说明Fig.2 Illustration of parameter in (5)

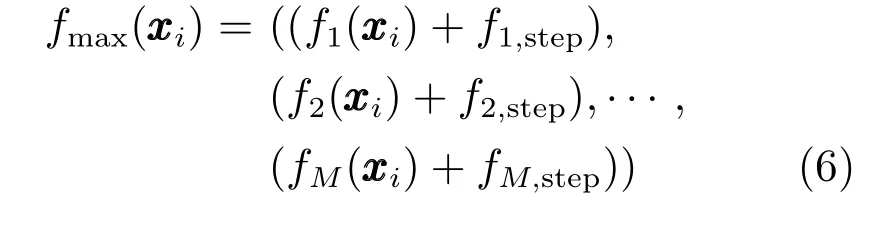
上述小种群划分过程可用算法2 描述,其中xi为随机选择个体.在初始阶段,首先确定目标函数平均距离(第1～2 行),在此基础上进一步确定xi所在小种群,并对小种群内未被标记个体进行逐一标记(第5～7 行).需要注意的是,在小种群划分过程中,平均距离和小种群划分的数量由种群在运算过程中确定.

根据式(5)～(7)可知,较大S 取值(例如当S取值为种群规模大小)会直接导致fj,step取值较大,从而导致fmax(xi)-fmin(xi)增大.由上述小种群划分过程可知,fmax(xi)-fmin(xi)较大取值不仅会导致更多个体包括在一个小种群中,而且也会减少小种群数量,并进一步减弱种群多样性.因此,在后续实验中,本文将采用较小S 值,且将验证不同S 取值对算法影响.

如图3 所示,通过以上方法可以将整个种群划分为若干小种群.每个小种群范围根据种群平均距离确定,且每个小种群相对于原始整个种群呈现大致均匀分布特点.正是上述特点才能保证最后所求结果均匀分布在Pareto 前沿面上,同时小种群有限的搜索空间也能保证整个小种群内部所有个体对前沿面进行有效探索.

图3 小种群划分示意图Fig.3 Illustration of small populations

算法2.平均距离多样性指标

算法3.基于平均距离聚类选择算子

2.3 基于平均距离聚类选择算子

如算法3 所示,在对小种群SP 执行选择时,首先判断随机选择个体aj与ai的支配关系.若可以确定支配关系,则较优个体被选择(第5～8 行).若aj与ai互不支配,则比较平均距离内个体数量,平均距离内个体数量少的个体被优先选择(第9～12行).如果aj与ai具有相同个体数量,则随机选择两者其一(第13～16 行).

利用上述策略对图1 进一步分析.由于点A 与点B 互不支配(第5～8 行),因此无法判断两者优劣.若将其所在小种群平均距离内个体数量作为进一步评判指标,则可有效区分两者优劣(第9～12行).由于A 非常靠近其邻居节点,因此在A 点平均距离范围至少有一个节点.对于B 而言,由于其与前后两个邻居距离适中,因此其平均距离内节点数为零.从上述分析中可以看出,利用本文所提的基于平均距离聚类选择策略可以有效避免选择拥挤度大的个体.

2.4 基于平均距离聚类交叉算子

与常规交叉算子不同,本文将小种群决策变量的平均距离加入到交叉算子计算过程中,即引入了扰动操作,从而可以进一步增加种群个体多样性.

一般交叉过程如图4 所示.在决策空间中,假设点A (小圆中心位置)和点B (小圆中心位置)为随机选择的交叉父代.按照标准交叉原则,A 与B 交叉子代一定落在小矩形框内(这里仅讨论交叉算子,不涉及变异,因此后代产生范围可以确定).如果引入基于平均距离聚类,则可以确定A 点所在的小种群范围(对应A 点所在小圆圈区域),同时确定B 点所在小种群范围(对应B 点所在小圆圈区域).通过随机选择A 点所在区域的个体A′和B 点所在区域的个体B′,A 与B 交叉产生的子代范围(实际是A′和B′进行交叉运算)将比标准交叉算子产生的子代范围更大(大矩形框所在区域).根据以上分析,可以看出采用基于平均距离聚类之后的子代区域搜索范围扩大了许多.

图4 交叉算子示意图Fig.4 Illustration of crossover operator

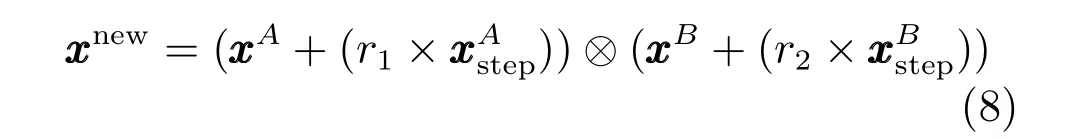
其中,xnew表示产生的子代,r1和r2分别是[-1,1]内的随机数.分别为A 点和B 点所在小种群每维决策变量的平均距离.

设A 点所在小种群为SPA,其个体数量为|SPA|,表示A 点所在小种群SPA第i 个个体第j 维决策变量,则小种群SPA中第j 维决策变量最大值与最小值分别为

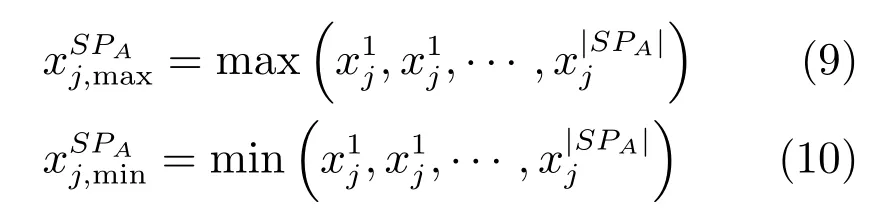
进而,可得A 点所在小种群第j 维决策变量的平均距离为

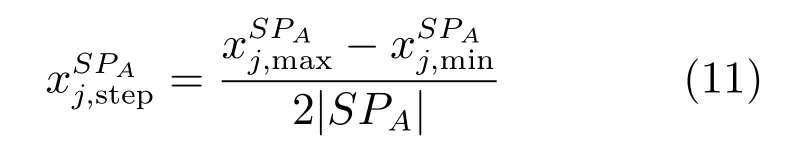
在每一维决策变量上计算决策变量的平均距离,可得到A 点所在小种群SPA在每维决策变量的平均距离,同理可以得到

2.5 基于平均距离聚类的NSGA-II 基本框架

基于平均距离聚类的NSGA-II 本质上是把平均距离聚类策略融入到NSGA-II 的选择和交叉算子中.它由5 个操作组成:平均距离聚类多样性指标、基于平均距离聚类的选择算子、基于平均距离聚类的交叉算子、变异算子和环境选择.

基于平均距离聚类的NSGA-II 主要过程如算法4 所示.在初始化种群和相关参数之后,首先对所有个体进行快速非支配排序,然后通过平均距离聚类的多样性指标把整个种群按照平均距离聚类划分为若干小种群,并根据小种群范围进一步确定每个个体所属小种群;利用基于平均距离聚类的选择算子在每个小种群内执行选择算子.根据个体支配等级和其所在小种群个体数量确定较优个体,并基于平均距离聚类交叉算子对小种群内部较优个体执行交叉运算.变异算子表示对所有个体进行变异操作,然后利用环境选择对整个种群个体更新.重复上述步骤,直到满足终止条件.需要说明的是,此处变异算子不涉及平均距离聚类,因此本文不再详述.环境选择为从父代种群和子代种群中选择较优个体,其主要涉及的选择算子与上面所述相同,因此也不再赘述.ADCNSGA-II 详细流程图如图5 所示.

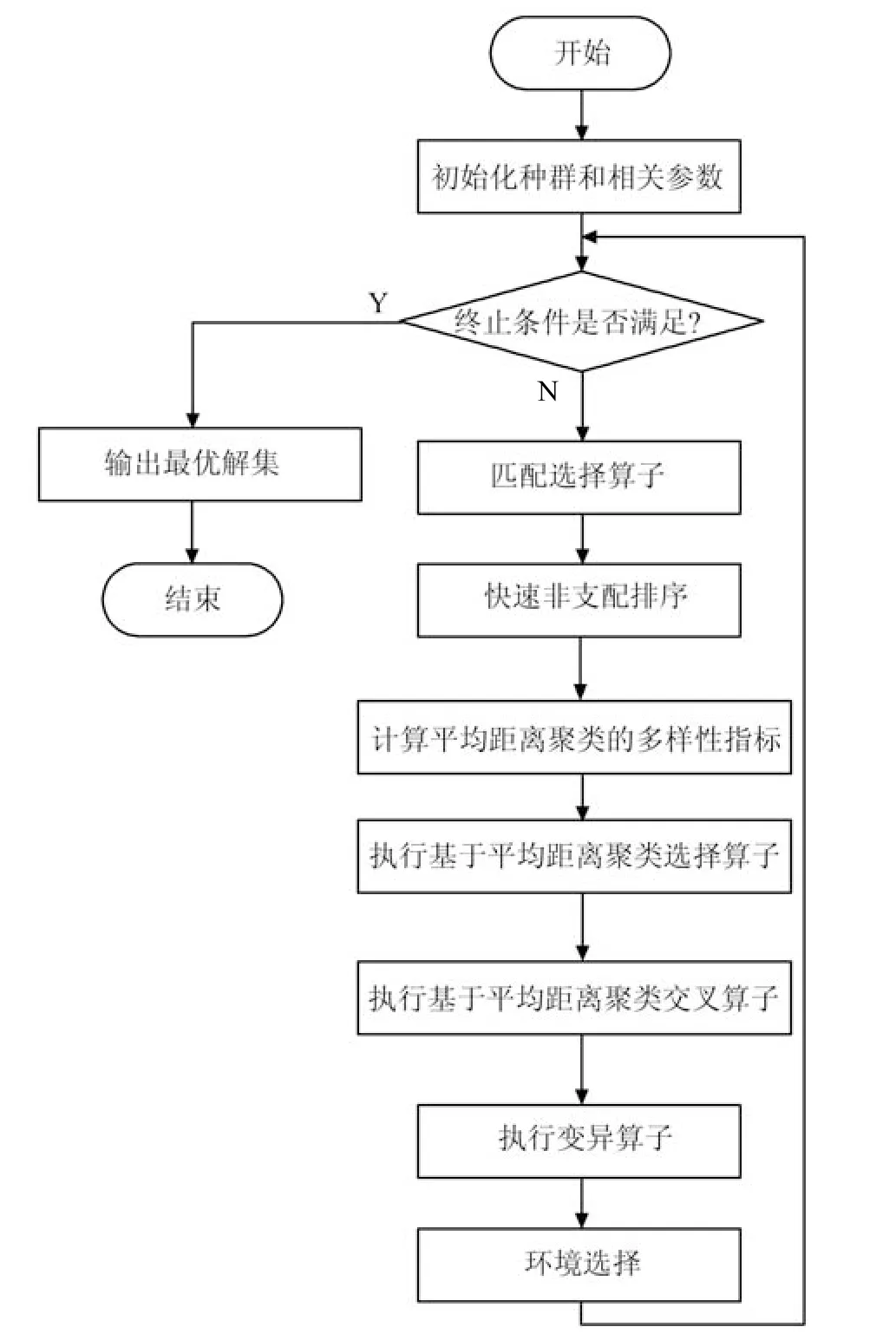
图5 ADCNSGA-II 算法流程图Fig.5 The flowchart of ADCNSGA-II

算法4.基于平均距离聚类的NSGA-II(ADCNSGA-II)

3 实验及结果分析

本实验分为两部分:1)分析ADCNSGA-II 中参数S 取不同值时对算法性能的影响;2)验证ADCNSGA-II 算法性能.为了综合测试算法性能,本文采用ZDT 测试函数集和SCH 测试函数.ZDT测试函数集[45]由Zitzler 等在2000 年提出,有6 个测试函数,本文采用其中5 个测试函数,SCH[46]由Schaffer 提出.这些测试函数具有凸、凹、连续、非连续和具有多重局部最优点等特点.

在多目标优化领域有很多评价指标,本文采用GD 值和SP 值作为评价标准,其中,GD[47]用于评价最终解集逼近真实前沿面程度,SP[47]用于评价种群分布多样性.通过对两个指标分别测试,可清楚地反映算法的整体性能.

3.1 参数SSS 对算法的影响

本小节研究参数对算法ADCNSGA-II 性能的影响.实验所用计算机为Inter Core i 5-2400 3.10 GHz CPU,6.00 GB 内存,Windows7 操作系统,运行环境为MATLAB7.9.每个算法独立运行30 次,算法最大迭代100 次,种群个体为50,分别取值为1,2,3,4,5和6.

不同S 取值对算法ADCNSGA-II 性能的影响如表1 所示.其中,mean(GD)和mean(SP)分别表示算法运行30 次后GD 值和SP 值平均值.同样,std(GD)和std(SP)分别表示算法运行30 次后GD和SP 方差.表中最优结果用粗体标注.从表1 可以看出,在ZDT4 测试函数上,不同S 取值对算法分布多样性和收敛效率有较大影响.但就整个测试函数而言,S=1 比S 取其他值时在算法性能上具有较大优势.就测试结果的数值变化范围而言,不同S 取值对算法性能并无明显差异.上述现象表明,较小S 取值(即每个小种群中个体数量较少),可以有效限制小种群内部个体变化范围;同时,也使多个小种群之间保持相对均匀的分布,进而保证整个种群的多样性.

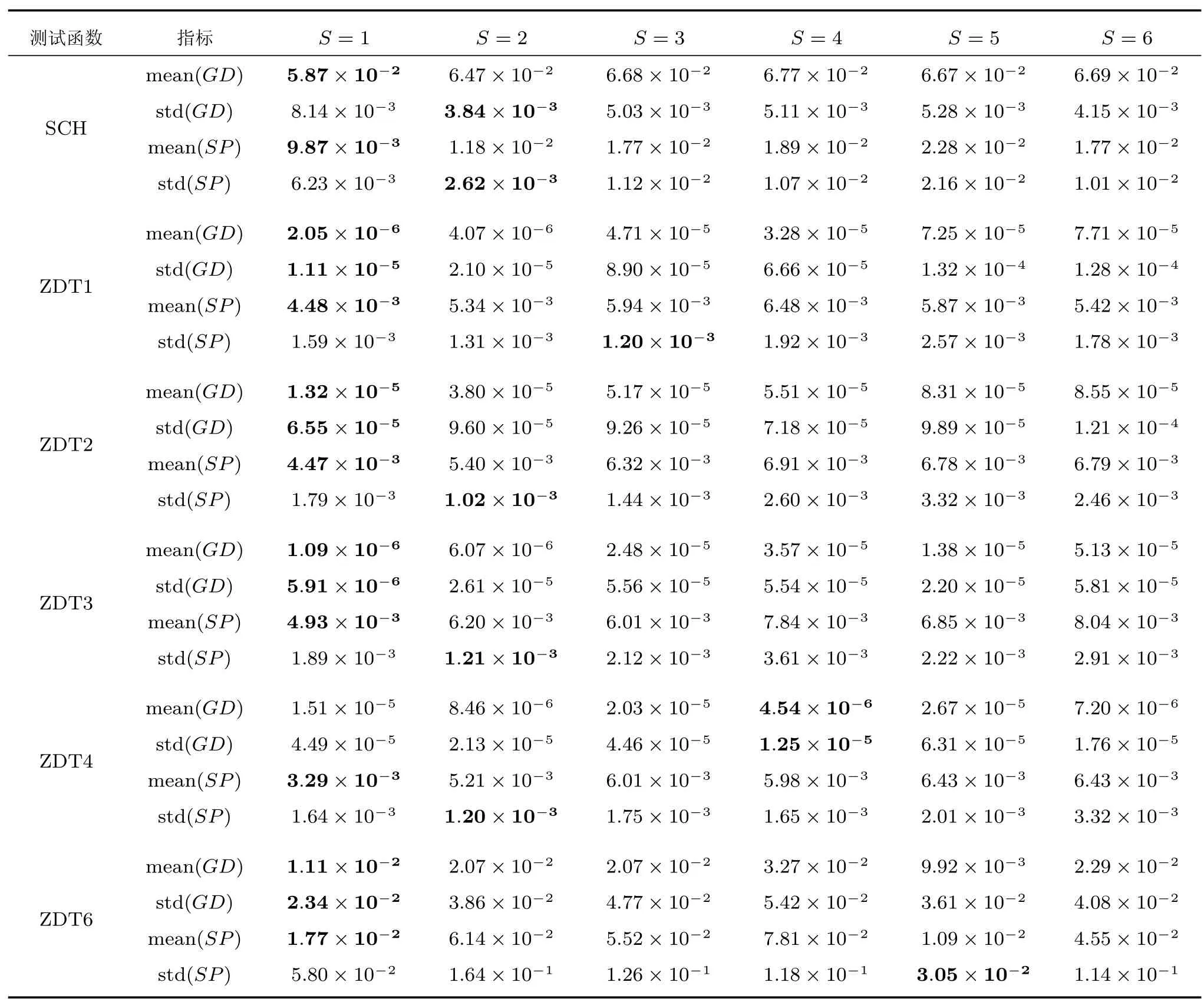
表1 参数S 对算法ADCNSGA-II 性能影响Table 1 Influence of parameter S on ADCNSGA-II

为分析不同S 取值对算法的影响,本文利用Friedman 检验和Wilcoxon 检验进一步分析上述结果.Friedman 检验用于分析多个样本之间的差异,根据秩均值大小排名,秩均值越小说明算法性能越好.Wilcoxon 检验用于分析两样本是否具有显著性差异.若p-value 小于0.05,则认为两个算法具有显著性差异.表2和表3 中所有数据根据算法运行30次平均GD 值求出.从表2 中可以看出,S=1 相对于S 取其他值时在ADCNSGA-II 上具有一定优势;从表3 中可进一步得出,不同的S 取值并没有导致算法具有明显的差异.从上述分析中可以得出,ADCNSGA-II 算法对于参数S 变化不敏感,即ADCNSGA-II 对参数S 具有较强的鲁棒性.

表2 Friedman 测试结果Table 2 Comparison results of Friedman test

表3 Wilcoxon 检测测试结果Table 3 Comparison results of Wilcoxon test

3.2 与其他算法实验结果对比

为了进一步分析ADCNSGA-II (即参数S=1)的性能,本文将其与NSGA-II[34]、PNIA[48]、SPEA2[15]和g-NSGA-II[49]进行比较,其中g-NSGA-II 是Molinac 等对NSGA-II 的进一步改进算法.从表4 可以看出,在ZDT1、ZDT3和ZDT4对比结果中,ADCNSGA-II 的性能明显优于其他四个算法;且在ZDT2 函数上,ADCNSGA-II和SPEA2 有相似的收敛性和分布性.对于SCH 测试函数,本文提出算法也具有相对较好的性能.在ZDT1～ZDT4 函数上,ADCNSGA-II 算法在分布多样性和逼近真实前沿面方面优于NSGA-II,在ZDT6 中,改进算法的收敛性明显优于NSGA-II.对比NSGA-II (此时相当于S 取值大小为种群数)和表1 中S=1,2,3,4,5,6 的实验数据,可以进一步验证前述结论.当S 取较大值时(例如S 为种群数量大小或者接近种群数量),由于每个个体在整个种群所在空间或者接近整个种群空间中变化,会导致整个种群多样性受到减弱;较小的S 值则可以有效限制小种群内部个体变换范围,且使多个小种群保持相对均匀分布,从而进一步增强种群多样性.从上述分析结果可以看出,ADCNSGA-II 有效地提高了算法多样性.同时,解集多样性又进一步提高了算法的收敛效率.

表4 实验性能均值和方差对比Table 4 Means and variances of the performance metrics

为了进一步分析ADCNSGA-II 与NSGA-II 差异,本文给出了两者之间的直观比较.从图6 可以看出,就解集分布多样性和逼近真实前沿面的能力而言,NSGA-II和ADCNSGA-II 算法在函数SCH、ZDT1和ZDT2 上具有相似求解结果;但在ZDT3函数上,ADCNSGA-II 在算法逼近最优前沿面方面明显优于NSGA-II,说明本文采用的基于平均距离聚类的多样性指标能有效提高算法收敛效率.ZDT4函数是几个测试函数中较为复杂的测试函数,它具有多个局部极值点.从ZDT4 及ZDT6 的对比效果来看,ADCNSGA-II 收敛效率明显优于NSGA-II.从上述分析中可以看出,ADCNSGA-II 不仅能提升解集分布性,而且可以间接提高算法收敛效率;出现上述现象的原因是由于种群多样性方面的提高使得个体间差异性变大,进而改善了全局搜索的效果.

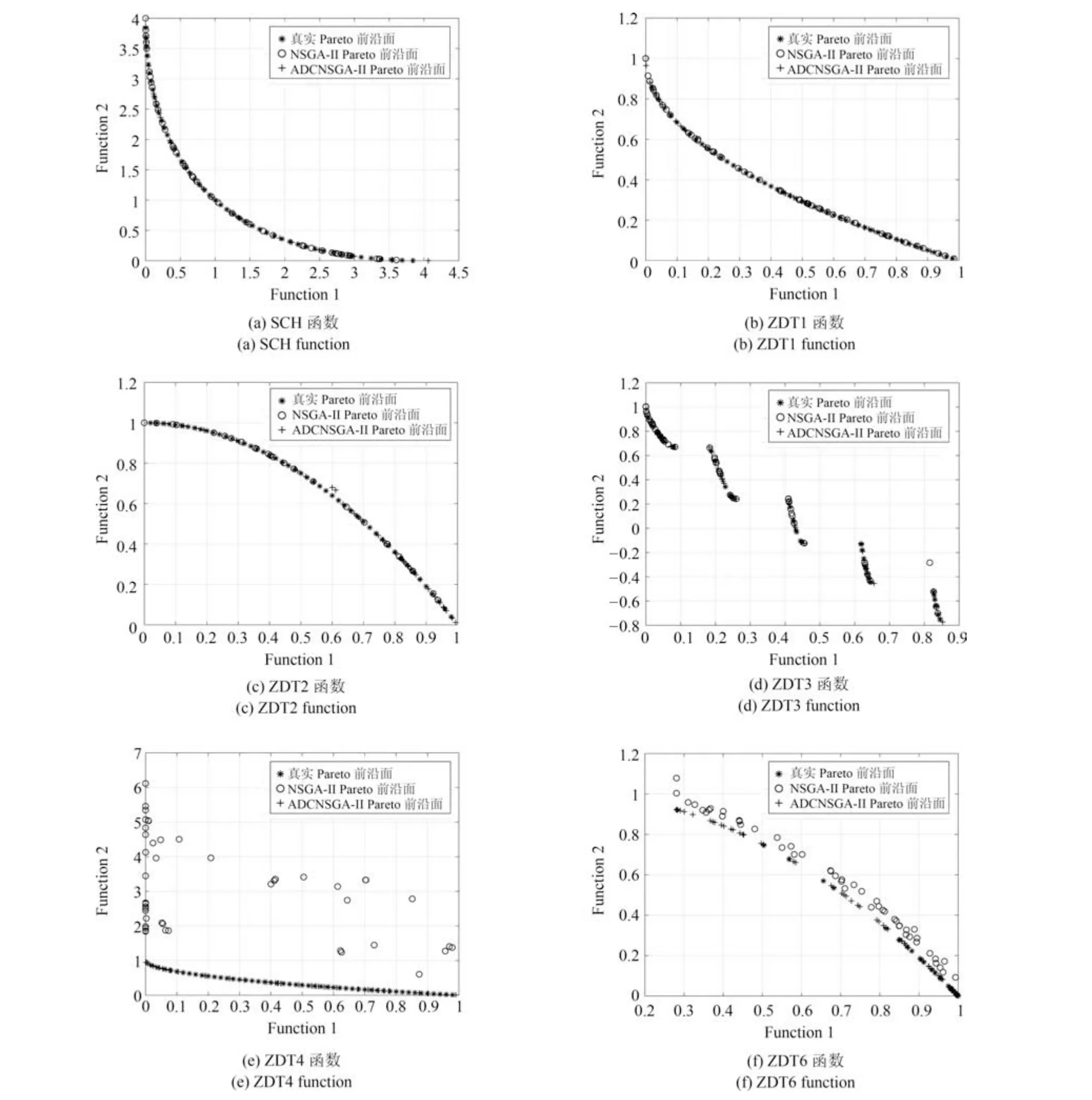
图6 测试结果对比Fig.6 Comparisons of obtained solutions

4 结论与展望

NSGA-II 具有较优收敛效率,但是其采用的拥挤度距离在某些情况下不能有效保持选择多样性.为了解决该问题,本文借鉴聚类思想,提出了基于平均距离聚类的多样性度量指标,并将其与NSGA-II融合,提出了ADCNSGA-II 算法.该方法利用平均距离将种群划分为若干个小种群,根据个体支配等级和平均距离内的个体数量选择较优个体,并在小种群内进行个体交叉和变异操作.实验结果表明,ADCNSGA-II 不仅有利于保持种群分布多样性,还可以间接提高种群收敛效率.在后续工作中,将会进一步完善平均距离聚类的多样性度量指标,引入其他聚类方法,使之适用于更多优化问题.