传感器饱和的非线性网络化系统模糊H∞H∞H∞滤波
李秀英 尹 帅 孙书利
随着通信技术和计算机技术的飞速发展,网络控制系统(Networked control system,NCS)已广泛应用于远程医疗、智能交通、航空航天等领域[1].网络的引入在给系统带来便利的同时,由于网络拥挤、信道衰减等原因,使得数据包在传输过程中出现了许多不确定性,如丢包、延迟以及乱序等.丢包现象如果处理不当,最终可能导致系统整体性能的急剧下降甚至崩溃,因此如何克服丢包带来的不利影响成为学者们普遍关注的问题[2-5].目前主要有4 种策略:1)零输入策略[2];2)保持输入策略[3];3)预报补偿策略[4];4)多包补偿策略[5-6].所谓多包补偿是指利用缓存器中的多个数据包来补偿丢失的数据.文献[5] 基于一步时滞和丢包的模型设计了滤波器、预报器和平滑器.文献[6] 针对多步时滞和丢包的系统设计了满足H∞性能指标的滤波器.但是,文献[5] 处理的只是线性系统,而文献[6] 虽然考虑了非线性干扰,但系统模型仍然是线性的.
控制工程中非线性对象普遍存在.Takagi-Sugeno (T-S)模糊模型[7]可以任意精度逼近定义在紧集上的非线性函数,已成功应用于复杂非线性系统的建模中[8-10].文献[8] 基于采样数据研究了网络化模糊T-S 系统H∞输出跟踪控制问题.文献[9] 针对一类带有双端丢包的T-S 模糊非线性系统提出一种丢包补偿策略.文献[10] 基于时滞分解技术,提出一种新的矩阵解耦方法设计了T-S 模糊系统的滤波器.然而,以上文献在选择Lyapunov 函数时都是独立于模糊规则的,这使得结果具有一定的保守性.
此外,工程上使用的传感器由于原理、制造技术以及使用安全等诸多因素限制,均无法识别或者提供幅值过大的信号,因而产生传感器件的饱和特性[11-15].文献[11-13]和[14-15] 分别研究了带有传感器饱和NCS 的H∞滤波和控制问题.对于某些类型的传感器,如霍尔传感器,频繁发生的饱和现象会造成器件损坏,失去测量的意义,不能再用于测量了.如何解决由于传感器饱和而导致的传感器失效时信号来源的问题也应引起重视.
基于上述分析,本文研究带有传感器饱和的TS 型模糊非线性系统的H∞滤波器设计问题.主要创新点如下:1)采用多包补偿策略克服数据传输过程中因丢失对系统性能产生的不利影响;2)针对传感器饱和而使器件损坏的问题提出传感器冗余方式解决信号来源问题;3)为减小设计的保守性,利用基于模糊规则依赖的Lyapunov 函数来分析系统的稳定性,得到使滤波误差系统渐近稳定,同时满足指定H∞性能指标的滤波器参数线性矩阵不等式(Linear matrix inequalities,LMIs)形式的解.仿真研究验证算法的有效性.
1 问题描述
1.1 非线性对象的T-S 模糊模型描述
考虑如下的非线性离散时间系统

假设1.f(xk)是一个光滑函数,满足条件f(0)=0,其中xk∈Rn是系统状态向量.
假设2.外部干扰输入wwwk∈Rq是能量有限信号,即wwwk属于平方可和的l2[0,∞)空间.
假设3.B 是已知矩阵,描述干扰对状态的影响.
对于非线性对象(1),用p 个T-S 型模糊规则去逼近.设第i 条模糊规则如下:
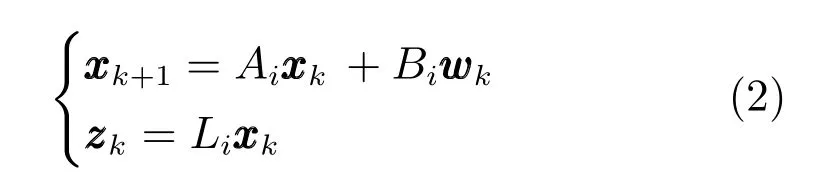
其中,θk=为前件变量,Wij(i,j=1,2,···,p)为模糊集合,zzzk∈Rm是待估计信号,Ai,Bi,Li是适当维数的已知矩阵.
注1.这里引入待估计信号zzzk更具有一般性.当Li为单位阵时,待估状态即为xk;当Li为一般向量时,待估状态为xk的某个分量或其线性组合.
利用中心平均解模糊器、乘积模糊推理,单点模糊器,可以得到模糊系统(2)的全局动态模型

注2.隶属度函数的选择没有统一的方法,可以根据需要适当选取.如果想要所选择的隶属度函数最优,可以引入智能优化方法(如粒子群算法、蚁群算法等)来优化隶属度函数中的参数.
1.2 饱和传感器的冗余策略
当传感器检测的信号幅值过大时,会产生饱和特性(如差压传感器、霍尔传感器).若传感器长时间处于饱和状态,会容易损坏,测量结果失去意义.为解决传感器饱和时信号来源问题,我们提出传感器冗余策略[16-17].输出yk∈Rr采用如下模型进行刻画
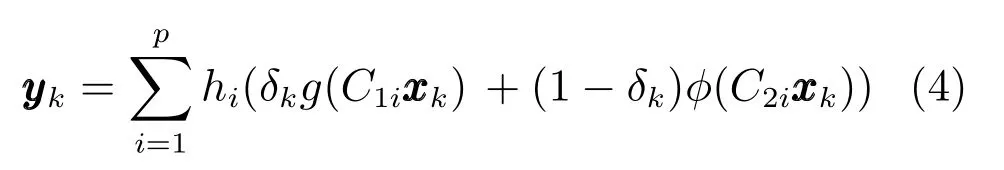
其中,Bernoulli 分布的随机变量δk用来表示主传感器和备用传感器之间的切换,且满足Prob{δk=1}=Prob{δk=0}=1-即δk=1 时表示主传感器工作,δk=0 时表示主传感器失效,此时启用备用传感器工作.传感器饱和用非线性函数g(C1ixk)和来描述,满足
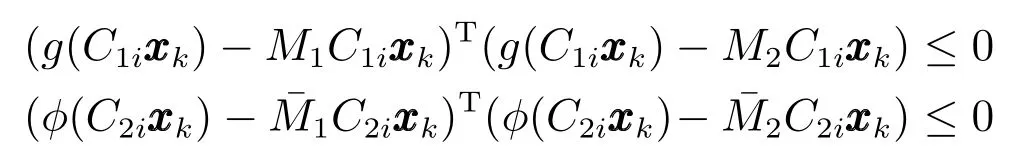
其中,M1,M2(M2>M1≥0),是常矩阵.为分析方便,将g(C1ixk)和分成线性部分和非线性部分来处理[13],即
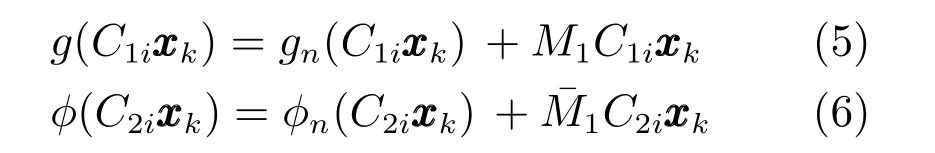
1.3 网络传输诱导现象的刻画
假设4.传感器是时钟驱动.
假设5.接收端设置缓存器.
网络环境下,无论是采用TCP 协议还是UDP协议,时滞和丢包现象不可避免[18].由于随机时滞的存在,使得在一个采样周期内,接收端接收到的数据可能是一个或是多个,也可能没有接收到任何数据,根据文献[19],采用如下模型来描述接收端的数据
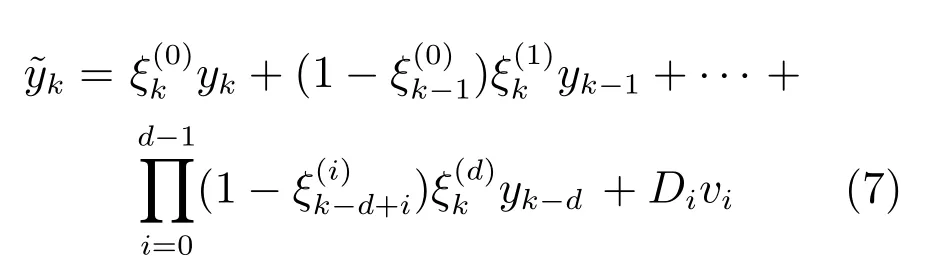
其中,Wk∈Rq是属于平方可和l2[0,∞)空间的观测噪声,d 是最大时滞;是相互独立的Bernoulli 分布的随机变量,且满足统计特性:
注3.当取不同值时,可以同时描述数据的丢失和d 步时滞的情况.易知,数据包正常接收的概率为d 步时滞的概率为丢包的概率为
1.4 模糊滤波器设计
针对T-S 模糊模型(2)描述的非线性系统(1),利用并行分布补偿技术,设计如下形式的满阶滤波器:
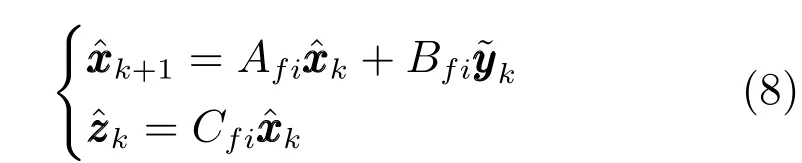
同样,可以得到滤波器的全局模型为
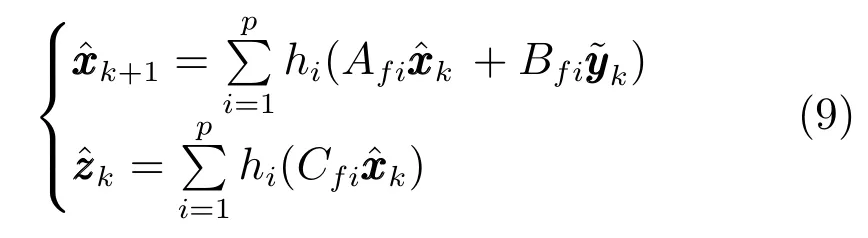
注4.也可以采用状态增广的方法设计滤波器,即引入状态然后为XXXk设计滤波器显然,增广方法会引起维数的增加.此处设计的满阶滤波器可以避免维数增加.
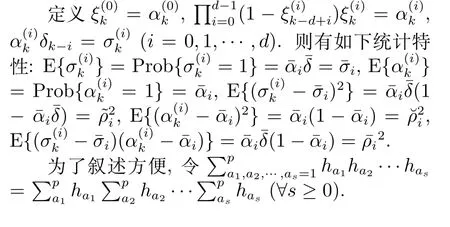
由式(2)~(4),(6),(7),可得滤波误差系统为
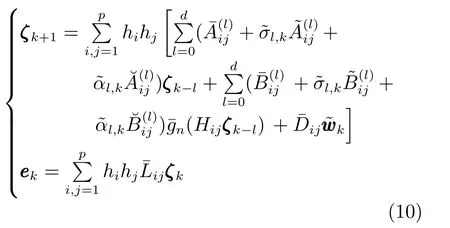
其中,

问题描述:针对基于T-S 模糊模型(2)描述的非线性系统(1),考虑传感器件的饱和特性以及观测数据到达接收端时可能发生的随机丢包和多步时滞的情况,设计形如式(8)的滤波器参数Afi,Bfi,Cfi,使得滤波误差系统(10)满足如下两个条件:
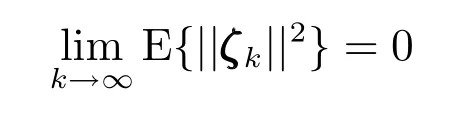
ii)H∞性能.在零初始条件下,对于所有的非零和指定的H∞性能指标γ >0,滤波误差ek满足如下H∞范数指标

引理1[20].对于对称正定矩阵S和任意适当维数的实矩阵Xij,有
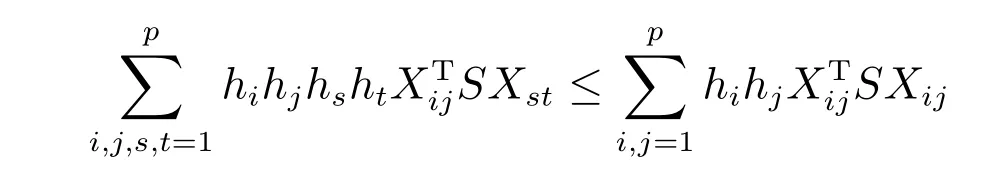
2 滤波性能分析
定理1.考虑基于T-S 模糊模型(2)描述的离散时间非线性系统(1),假设滤波器参数Afi,Bfi,Cfi已知,则滤波误差系统(10)是均方意义下渐近稳定的,且当时,系统(10)满足指定H∞性能指标γ,如果存在模糊规则依赖的正定对称矩阵Pq>0,Qj>0 (q=j=1,2,···,d)及标量εi>0(i=0,1,···,2d+1),使得如下矩阵不等式成立

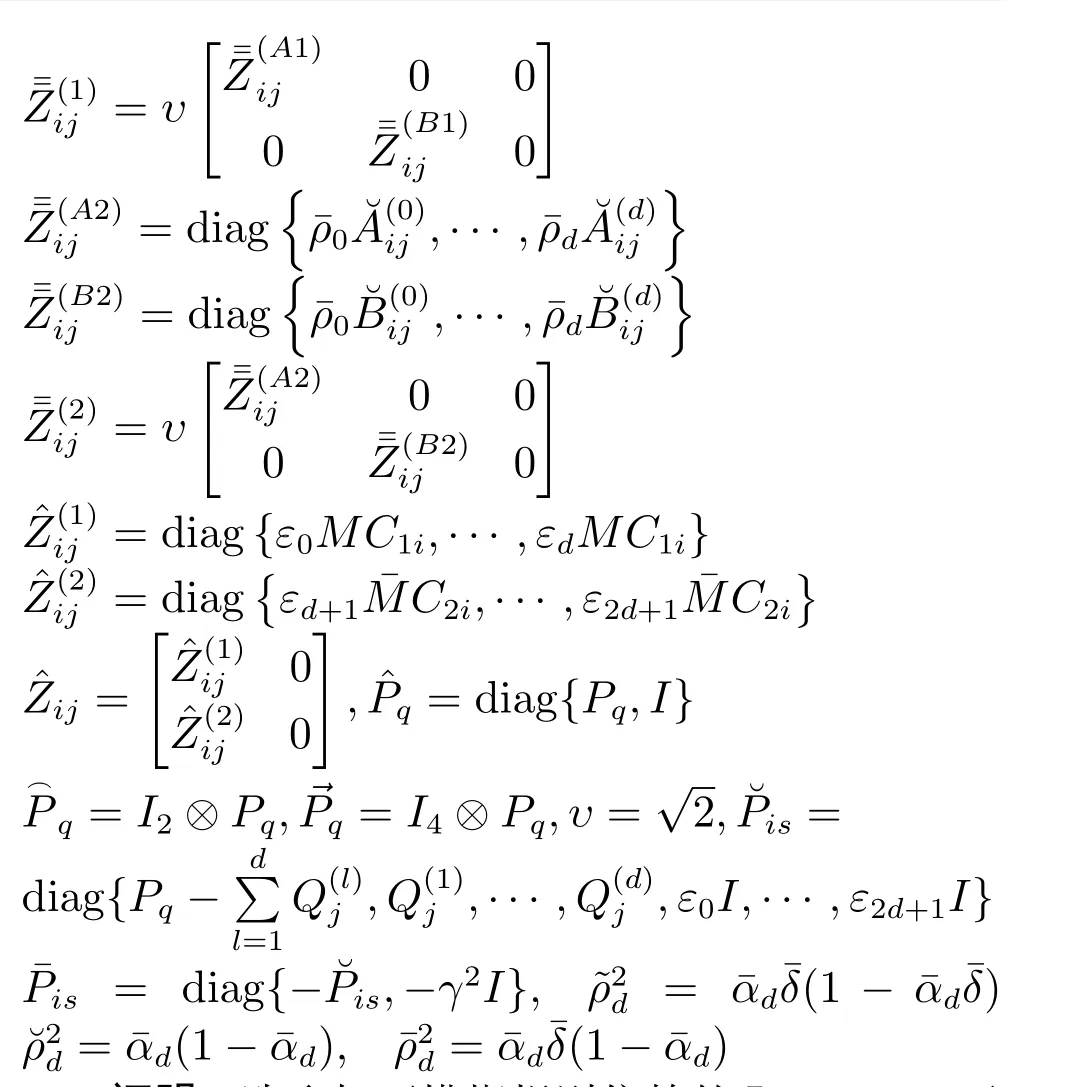
证明.选取如下模糊规则依赖的Lyapunov 函数
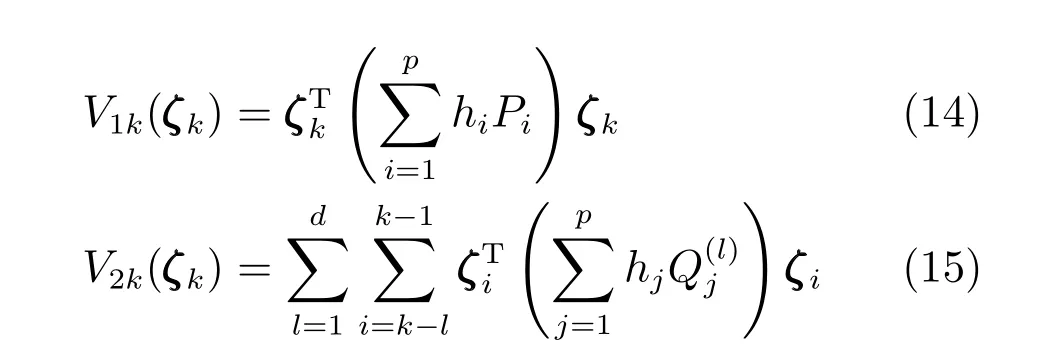
那么
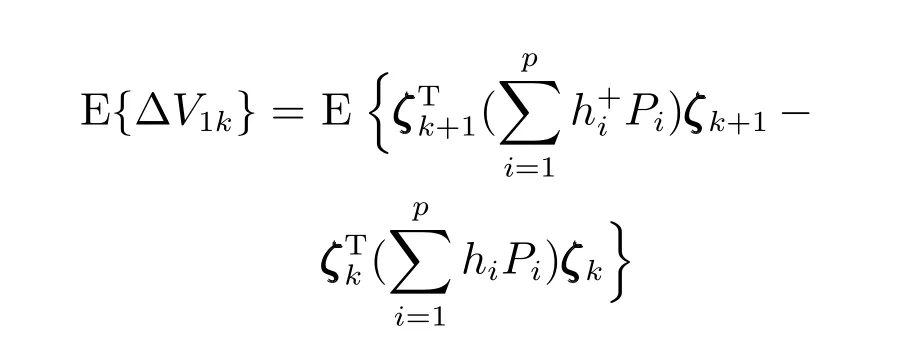
将滤波误差系统(10)代入上式,有

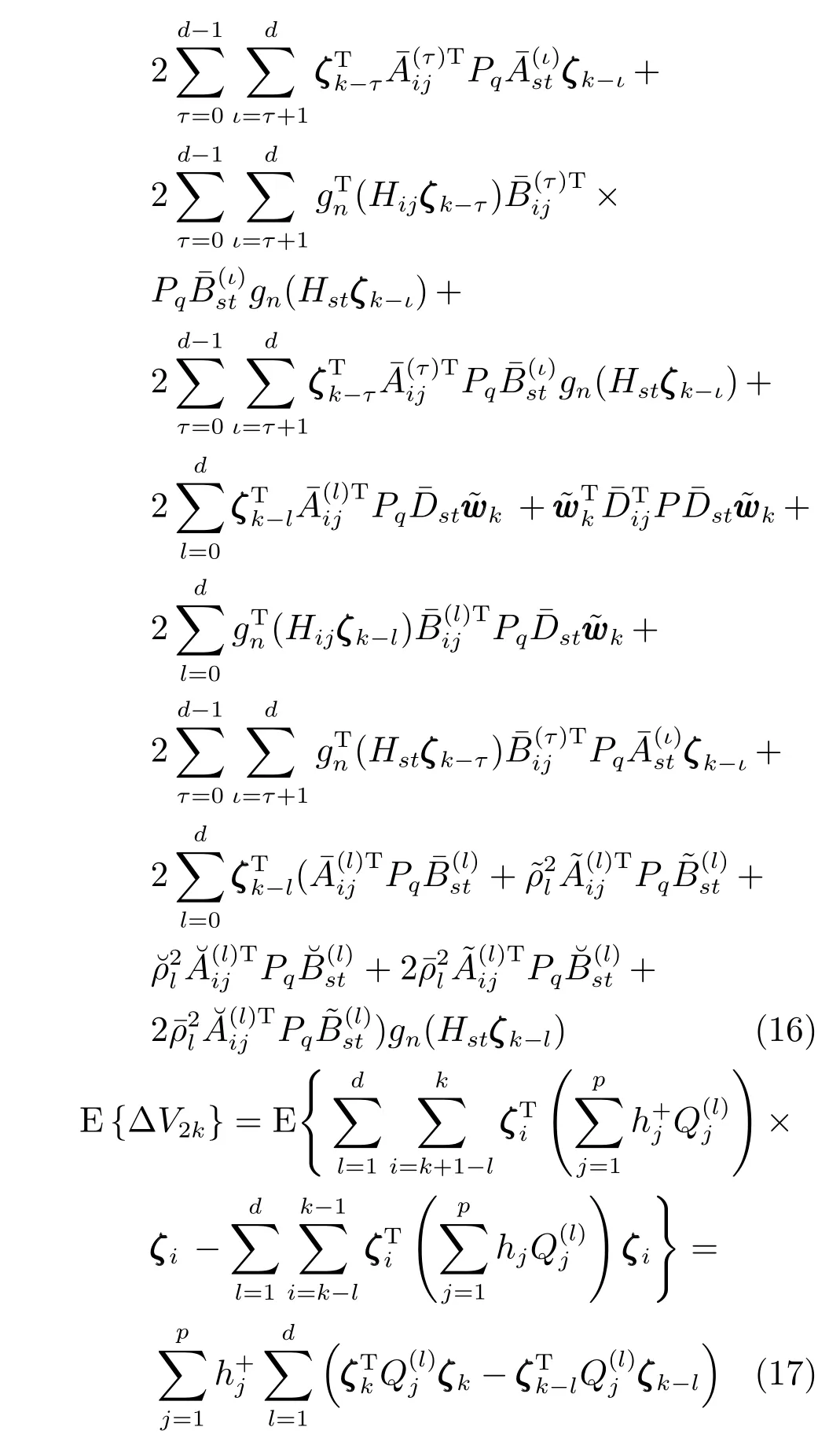
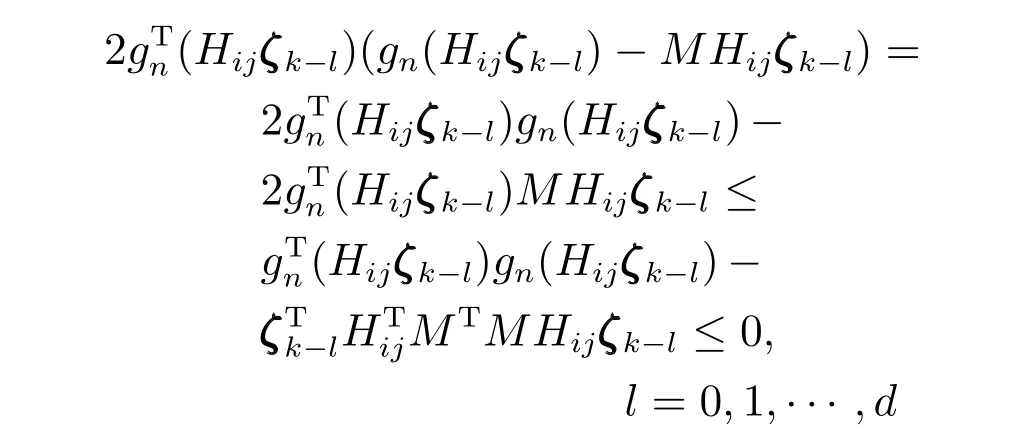


首先证明当~wwwk=0 时滤波误差系统(10)是均方意义下渐近稳定的,有
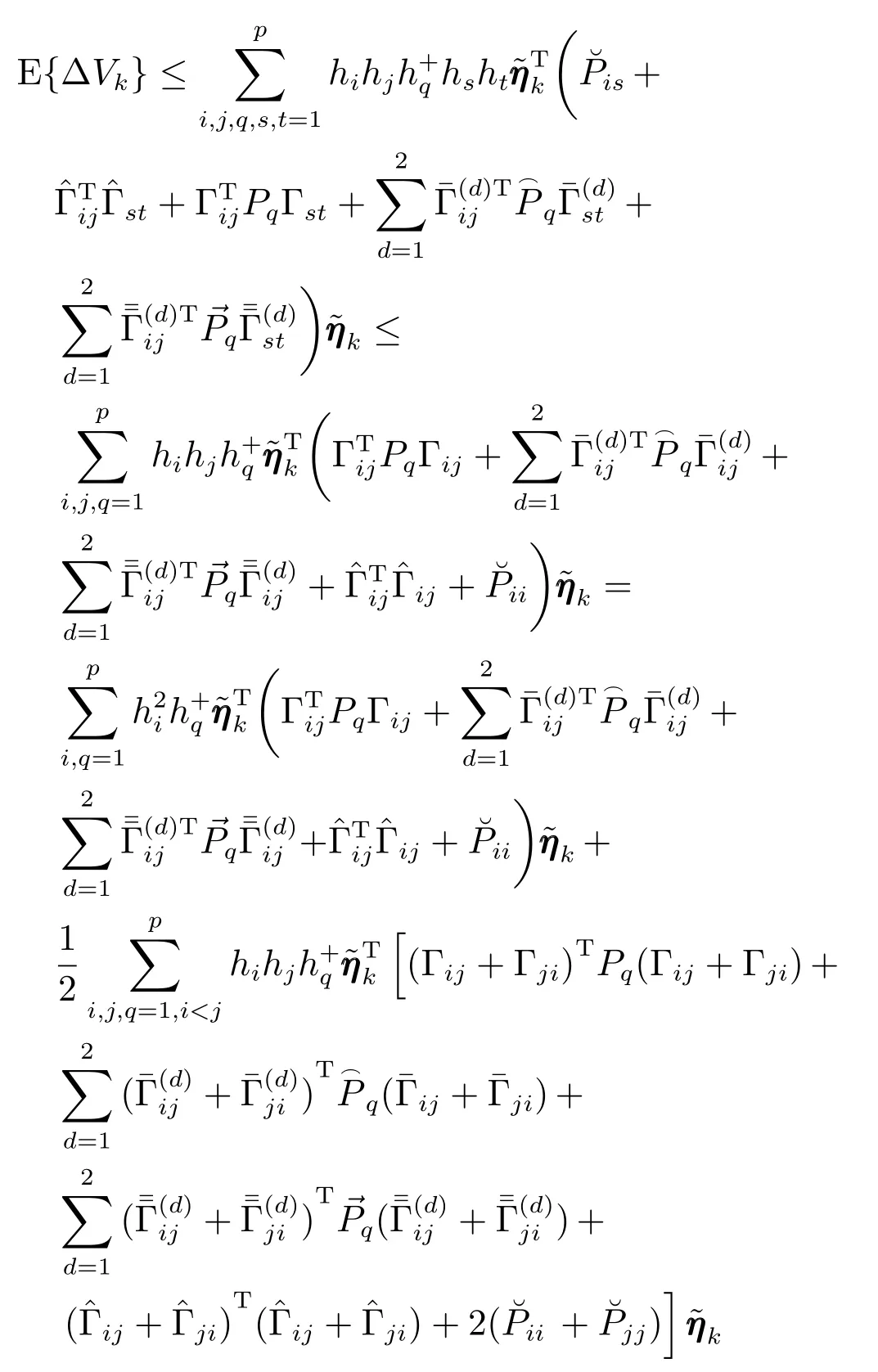
由Schur 补引理可得,E{ΔVk}<0 当且仅当不等式(12)和(13)成立.根据Lyapunov 稳定性理论可知,当时,滤波误差系统(10)是均方渐近稳定的.接下来,为分析滤波误差系统(10)的H∞性能,引入目标函数
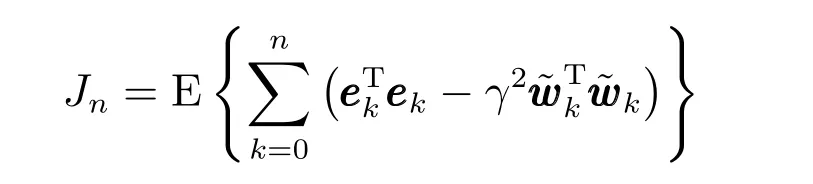
显然,为证明H∞性能指标(11)成立,即要证明在零初始条件下有Jn<0 成立.于是,有
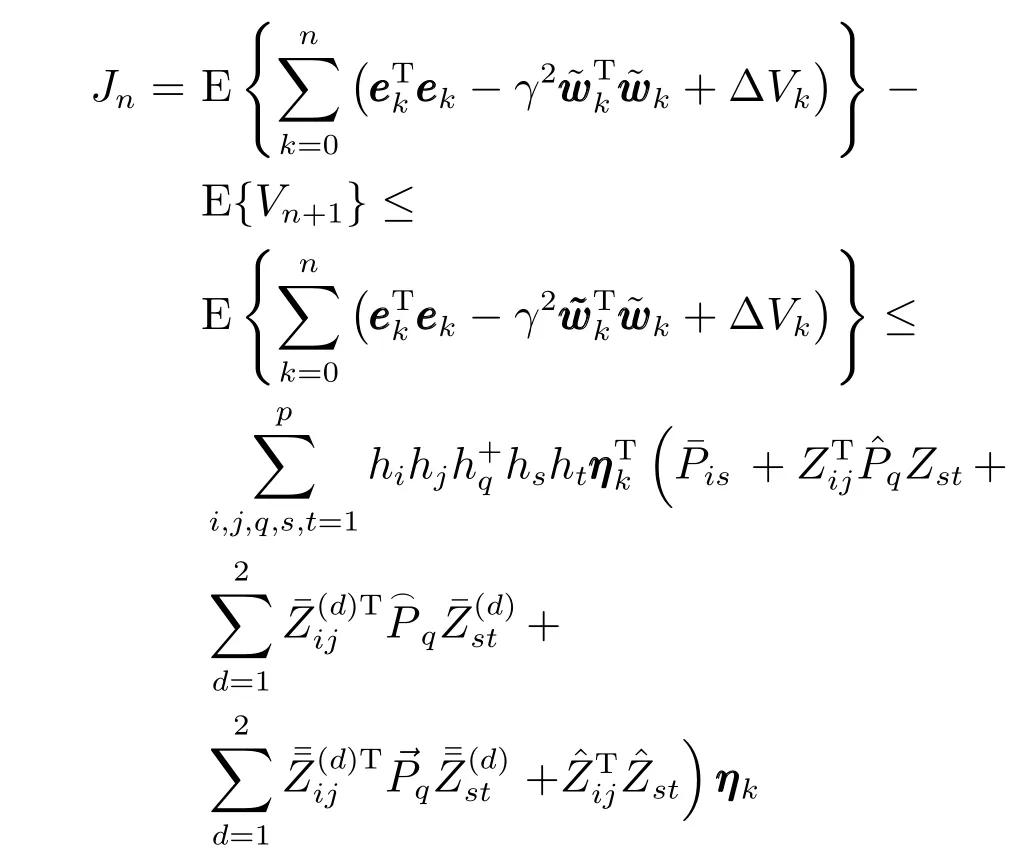
类似于前面的推导过程,可得
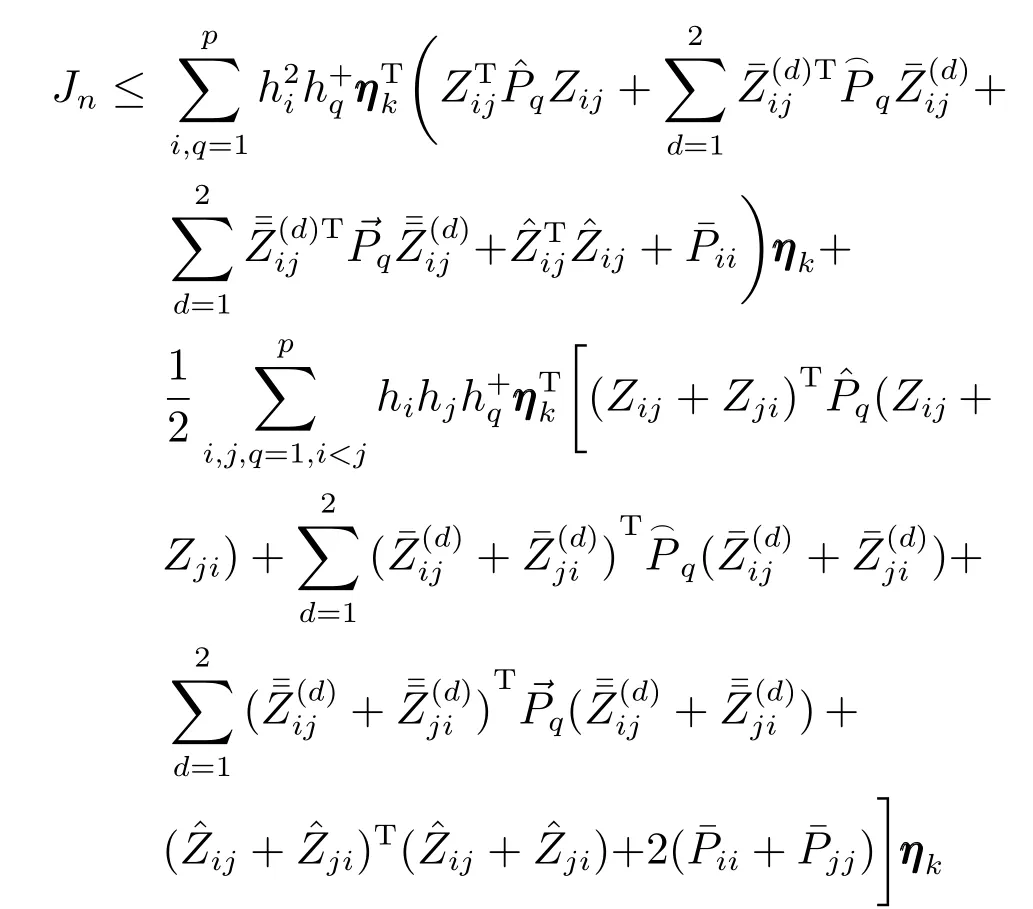
由式(12)和式(13)可知Jn<0.令n →∞,易得

3 H∞滤波器设计
定理2.考虑基于T-S 模糊模型(2)描述的离散时间非线性系统(1),在传感器饱和及数据包丢失和时滞存在的情况下,对于给定标量γ >0,存在一个H∞滤波器使得滤波误差系统均方意义下渐近稳定,且当时,H∞性能指标(11)成立,如果存在模糊规则依赖的矩阵1,2,···,d),矩阵和标量εi>0 (i=0,1,···,2d+1),使得如下LMIs成立

其中



若不等式(18)和(19)存在可行解,则滤波器参数为
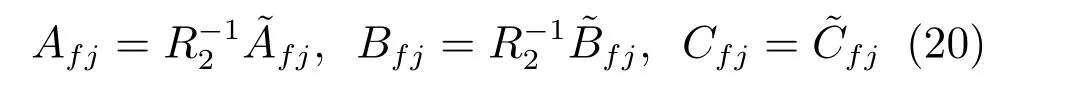
证明.由Schur 补引理,可以将定理1 中的矩阵不等式(12)和(13)写成如下形式:

注5.由不等式(18)和(19),通过求解如下凸优化问题1可以得到系统的最优H∞性能指标为其中为的最优值.
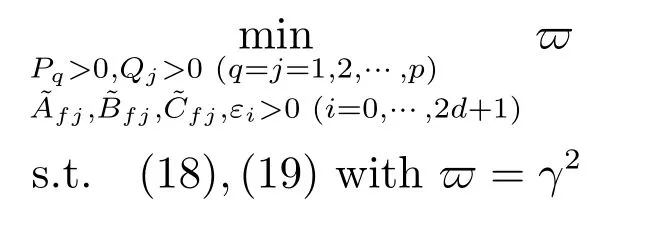
注6.在一些场合下,基于模糊模型(2)对非线性系统(1)的建模会存在一定的建模误差.考虑近似误差后,非线性系统(1)可以等价于如下系统
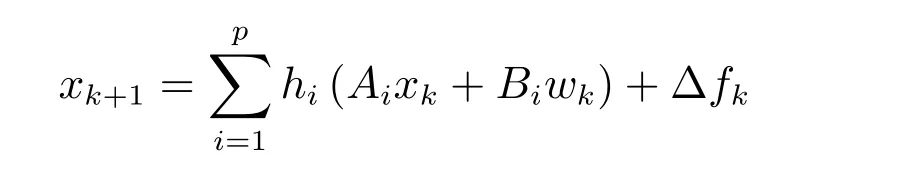
4 仿真例子
为验证本文所提算法的有效性,考虑文献[21]中的一个非线性倒立摆系统
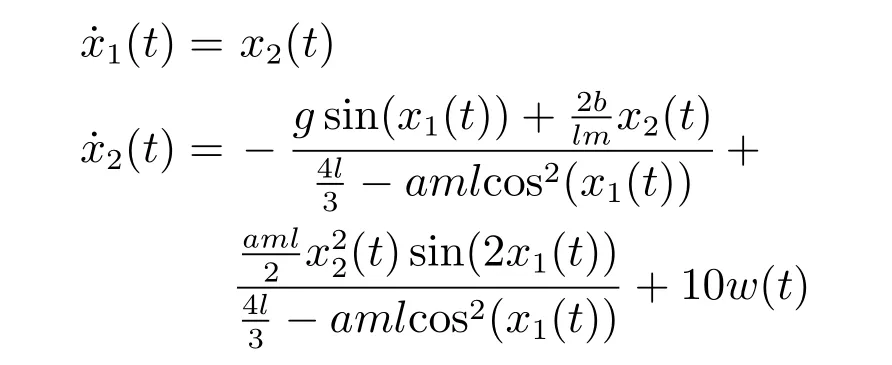
其中,x1(t)表示倒立摆与垂直方向的角度,x2(t)是角速度,g=9.8 m/s2是重力加速度,m 是倒立摆的质量,a=1/(m+M),M 是小车的质量,2l 是倒立摆的长度,b 是倒立摆与轴之间的阻尼系数,w(t)是干扰输入.根据文献[21],取m=2 kg,M=8 kg,l=0.5 m 以及b=0.5 Nm/s.将系统在原点以及x=(±60°,0)处线性化,以采样周期T=0.01 s 离散化,可得该系统的离散时间T-S 模糊模型为
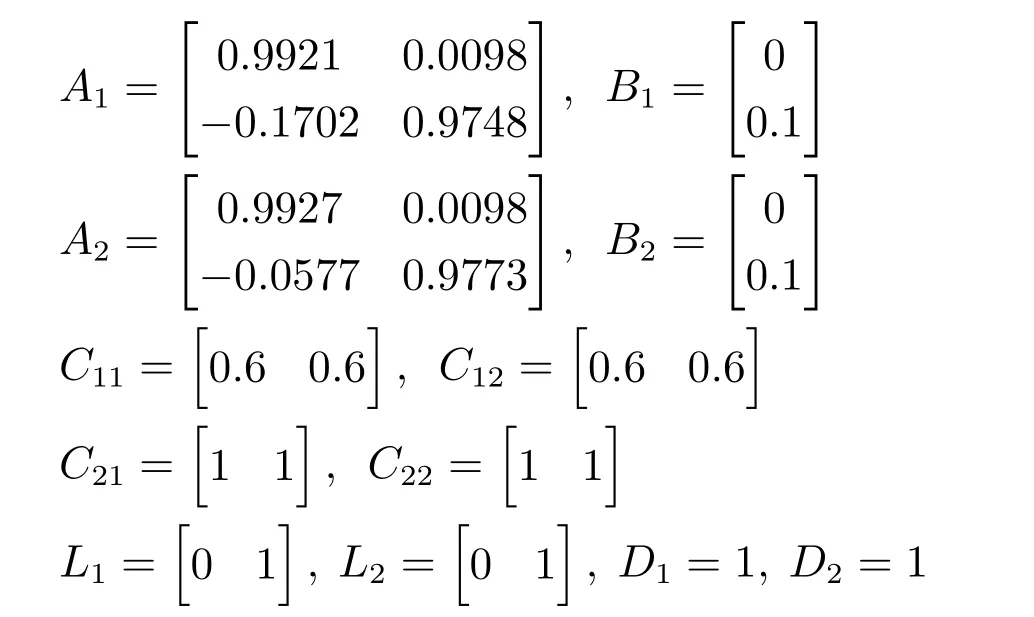
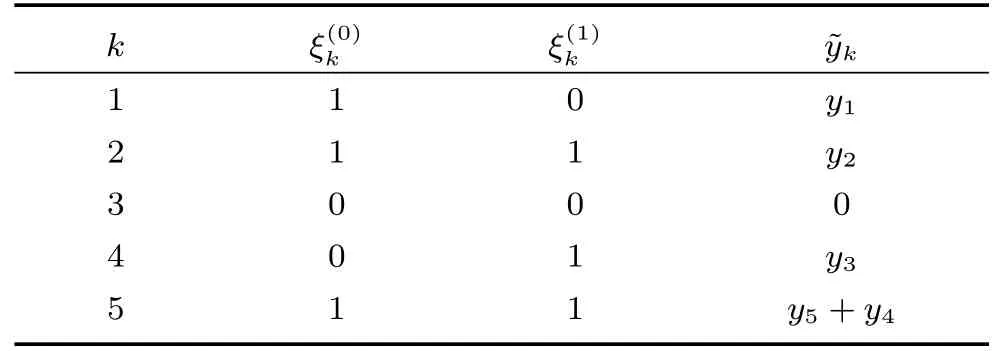
表1 接收端接收数据情况举例Table 1 An example case of the received data at the receiver side
通过求解问题1,可以得到最优的γ*=5.7774,滤波器参数为

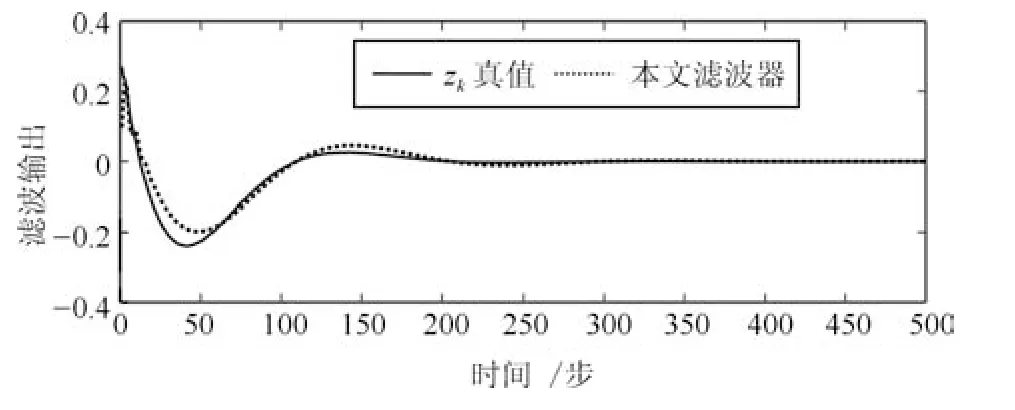
图1 zk 真实值和H∞滤波值Fig.1 True value of zk and its filter
为说明基于模糊规则依赖思想所设计的滤波器可以降低保守性,将本文与模糊规则独立方法(即选取Lyapunov 函数时Lyapunov 矩阵与模糊规则无关)进行比较.参数保持不变,令从0.1 到0.9 变化,所得的最优H∞性能指标γ*结果如表2 所示.从表2 中可以看出,模糊规则依赖的方法所得的γ*要小于模糊规则独立的方法,即可以有效降低设计的保守性.同时,随着数据包正常接收的概率增大(即变大),H∞性能指标γ*减小,系统的抗干扰能力增强.

表2 模糊规则依赖与模糊规则独立的γ* 比较Table 2 Comparison of γ* between fuzzybasis-dependent and fuzzy-basis-independent methods
我们进一步分析了主传感器和冗余传感器对系统性能的影响.当不变,而从0.2 变到1时,所得的最优H∞性能指标γ*由表3 给出.由表3 可知,随着的增大,γ*也随之增大.即备用传感器的性能较主传感器的性能更好.

表3 最优H∞性能指标与传感器饱和发生概率¯δ 的关系Table 3 Relation between optimal H∞performance and the sensor saturation occurrence rate
为了说明时滞概率与丢包概率对系统性能的影响,我们分别给出最大时滞为一步与最大时滞为两步时的仿真结果,如表4 所示.从表4 中可以看出,在正常接收概率相同的前提下,当丢包概率相同,最大时滞为一步时的最优H∞性能指标γ*较最大时滞为两步时的要小,即随着系统的时滞变大,系统性能变差.同时,当系统正常接收的概率变大,随着系统丢包概率的减小,γ*也随之减小,系统的干扰抑制性能变好.

表4 最大时滞为一步与两步时的γ* 比较Table 4 Comparison of γ* between one-step and two-step maximum delays
最后,我们在表5 中给出了与文献[22] 的仿真比较结果.文献[22] 考虑的是带有传感器饱和的NCS 模糊H∞滤波器设计,但接收端只有一个数据用于滤波器设计.为了比较,令本文算法中¯δ=0,文献[22] 中的最大时滞为d=1 (即数据被正常接收,延时一步接收,或者丢失).在相同的正常接收概率和一步时滞概率的前提下,我们比较了最优H∞性能γ*.从表5 中可以看出,本文方法所得γ*的结果比文献[22] 的要小.原因主要有两个方面:一是本文采用的是多包补偿策略,二是在设计时选用的模糊规则依赖的方法.
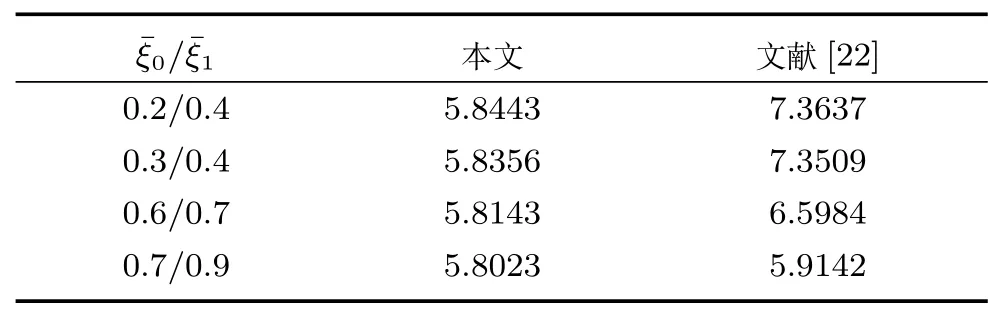
表5 与文献[22] 中方法的γ* 比较Table 5 Comparison of γ* with the method in [22]
5 结论
网络控制系统中的被控对象通常是非线性的,而负责采集数据的传感器也会出现饱和非线性现象.本文针对带有传感器饱和的T-S 模糊模型描述的非线性系统,对于传感器饱和可能带来的器件损坏问题,提出冗余策略来解决信号来源问题,并利用多包补偿策略改善丢包对系统的影响.基于模糊规则依赖的思想,利用随机分析方法得到了使滤波误差系统均方渐近稳定且满足指定H∞性能的一个充分条件,利用LMI 技术得到滤波器参数的解.仿真分析结果表明,模糊规则依赖的方法比模糊规则独立方法可以获得较小的保守性,同时随着系统时滞的增大,系统的性能变差.本文所采用的T-S 模型可以很好地逼近系统的非线性,但在实际中,系统的不确定性也是广泛存在的.针对系统不确定性的处理,可以有两种方法:一是采用区间2 型T-S 模糊模型[23],该模型利用隶属度函数的上界和下界来刻画系统的不确定性;二是设计自适应模糊系统[24-25],即通过适当的方法来在线调整系统参数,以适应系统的不确定性.这两个问题将是作者后续研究的主要方向.

