一种单因子的可撤销生物特征认证方法

孔小景 李学俊 金 哲 周 芃 陈江勇

身份鉴别是个人利益和国家安全的重要保证,生物特征作为身份鉴别的一种重要工具,因其不可代替性和便携性而受到学者与产业界的青睐[1－2].例如,生物特征识别系统被广泛应用于国防安全、互联网金融、海关出入境等多个领域[3－4].随着生物特征识别系统应用的普及,生物特征存在一旦丢失无法重新发布的隐患逐渐显现出来.为此生物特征模板保护成为身份认证领域的研究热点.

双因子可撤销生物特征模板保护方法是生物特征模板保护的主流方法之一,需要附加用户特定参数(通常以密码或令牌的形式出现)与生物特征一起作为输入[1,5].该方法需要用户引入额外的输入因子,存在一些问题,例如:保留令牌或记忆密码给用户带来了不便,以及外部因子可能被盗、丢失或遗忘等[6].基于单因子的可撤销生物特征模板保护是一种新的生物特征模板保护方法[7],将生物特征作为唯一的输入因子,解决了上述双因子可撤销生物特征模板保护中外部因子产生的问题.

本文基于文献[7] 中单因子的可撤销生物特征认证系统的框架,提出了一种新的解决方法,即滑动提取窗口哈希(Window sliding and extracting Hashing,WSE)算法.与文献[7] 中方法相比,该方法改进了滑动窗口取值与哈希函数模块,并以指纹模板的二进制矢量形式[8]为例,在FVC2002和FVC2004 的两个公共指纹数据集中的4 个数据库上进行实验.实验结果表明,本文提出的方法不仅满足可撤销生物识别技术设计的4 个标准,而且能抵御3 种安全攻击.

本文方法的主要贡献如下:

1)建立了WSE 哈希算法的单因子可撤销生物特征认证模型,提高了可撤销模板的精确性;

2)采用了跳位取值的滑动窗口哈希算法技术,提高了可撤销模板的安全性;

3)增加了一个评价维度,即唯密文攻击,更加全面的评价本文方法的安全性.

本文的其余部分安排如下:第1 节介绍相关工作,第2 节描述了一种单因子的可撤销生物特征认证方法,第3 节给出了性能分析,第4 节对安全性进行了分析和讨论,最后,第5 节给出了总结与展望.

1 相关工作

生物特征模板保护通常可分为两大类[1]:可撤销的生物特征识别和生物特征加密系统.前者包括生物特征加盐法和不可逆形变法,后者包括密钥绑定系统和密钥生成方案.本文的研究重点是可撤销的生物特征识别.

一般来说,可撤销的方案通常被设计为参数化认证机制,要求用户提供生物特征标识符和密钥.用户特定的密钥通常存储在令牌的外部存储器(例如,个人的存储器或物理硬件)中;因此,可撤销的方案也通常被称为“双因子”或“令牌化”生物特征认证方案.另一方面,“单因子”或“无标记”方案要求用户仅提供用于认证的生物特征标识符,并且单因子方案的工作量非常少.单因子方案中的服务器负责存储注册模板和密钥.在单因子方法中,即使模板和密钥被破坏,攻击者也很难获得原始模板.不考虑转换策略(即盐基和不可逆转换)和生物统特征的形式,本节介绍了双因子和单因子可撤销的生物特征识别方案的相关工作.

Biohashing[5]利用用户特定的令牌生成可撤销的模板(参见bioCodeb).如图1,通常,Biohashing 方法把生物特征向量x∈Rn和正交随机矩阵R ∈Rn×q作为输入,其中q ≤n.Biohashing 方法中的可撤销生成过程如下:1)通过计算x=RTx形成内积矢量y;2)根据预先定义的阈值τ 将y进行行二值化运算,生成bioCodeb∈[0,1]q,如式(1)所示:

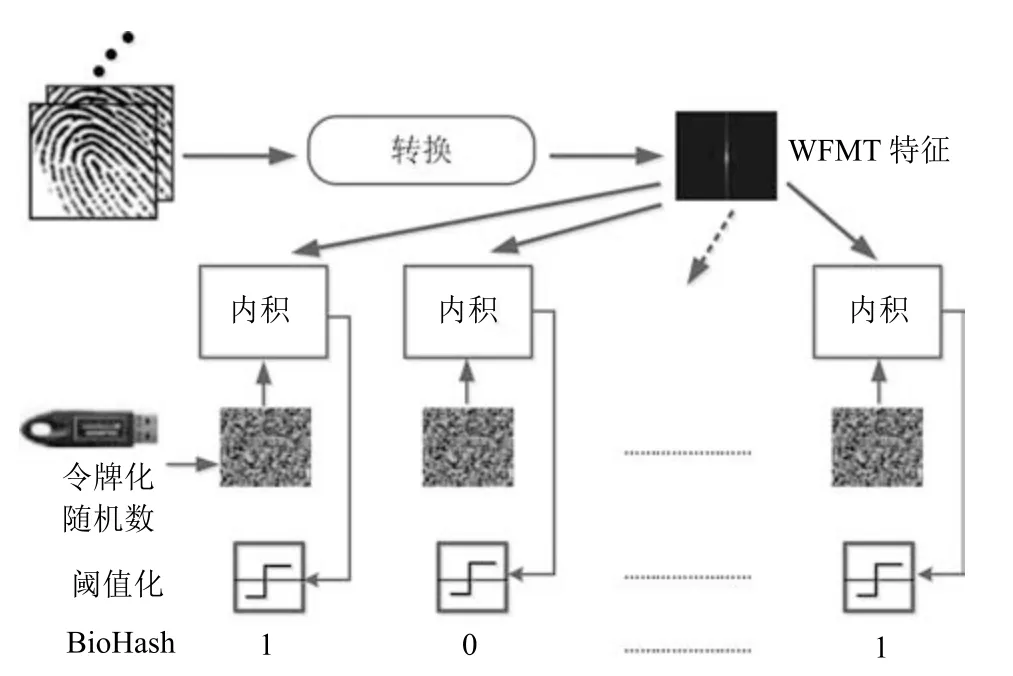
图1 Biohashing 转换概述图[5]Fig.1 Overview of Biohashing transformation[5]

其中,i=1,···,q.Biohashing 方法可以推广到其他生物特征形式,例如,面部、虹膜、手掌等.Bio-Hashing 是一种典型的生物特征加盐法,其他的加盐法如文献[9-10],这些基于加盐的方法具有共同的特征,即它们利用外部用户特定因子来生成转换矩阵并与生物特征模板相乘或卷积,当模板受到攻击时,可以通过改变令牌从而撤销已有模板并生成新模板.此外,文献[11] 阐述了利用折衷的可撤销模板和正交矩阵获得原始生物特征模板的可行性.

Wang和Hu[12]提出了一种可撤销的指纹生物识别技术,即“Densely infinite-to-one mapping(DITOM)”映射.该方案在匹配过程中不需要对准过程,利用多对一转换机制,来生成用于匹配的可撤销模板.简而言之,该方案将每个细节点对量化为二进制字符串,之后进行离散傅里叶变换(Discrete Fourier transformation,DFT)将二进制串转换为复数向量C.再通过将随机生成的参数密钥R 与复向量组合来生成可撤销模板T.组合函数描述如式(2)所示.

与将生物特征数据和密钥组合以生成模板的Biohashing 不同,该方法从生物特征数据生成不可逆实例,然后将不可逆实例与密钥组合以生成可撤销模板.

布隆过滤方法(Bloom filter)是由Rathgeb等[13]提出的可撤销生物识特征别技术,首先应用于虹膜模板保护,后来被推广到面部、指纹和多模态生物特征识别等多种生物特征形式.在文献[13]中,Bloom filterb是一个长度为n 的用0 初始化的bit 数组.然后,应用K 个独立的哈希函数根据输入项生成一组十进制值h∈[0,n-1]K.之后,通过增加b中元素的值来形成最终b,其中h中的值表示要增加的元素的位置.该技术中不是使用哈希函数,而是提出二进制到十进制映射函数来生成用于匹配的b∈[0,1][13].基于Bloom filter 转换的过程如图2 所示[13]:1)给出一个具有H ×W 维度的IrisCode,将IrisCode 细分为维度为H ×l 的多个子矩阵B,其中l=W/K,K 是子矩阵的数量;2)对于每一个Bi,其中i=1,2,···,K,当w=H时,用0 来初始化Bloom filterbi∈[0,1]2w;3)在每个Bi中,逐列对元素执行二进制到十进制转换以生成一组十进制数;4)根据在3)中转换得到的十进制数,将Bloom filterbi中的元素设置为1,其中十进制数的值表示bi中元素的索引;5)重复步骤2)～4),直到形成K Bloom filterbi.注意,在步骤4)中,如果转换了两个相同的十进制数,则bi中的元素仍设置为1,因此,实现了多对一映射.为了实现可撤销性,在基于Bloom filter 转换之前,将原始的IrisCode和特定的秘密T 做异或(XOR)运算.尽管Bloom filter 方法具有良好的不可逆性(多对一映射),但它不能满足不可链接性标准[14].Hermans等[14]说明了由相同的IrisCode和不同的T 生成的两个Bloom filters 之间的高匹配分数(最高96%).此外,Bringer 等[15]指出当密钥空间(T)太小时,Bloom filter 方法容易受到暴力攻击.

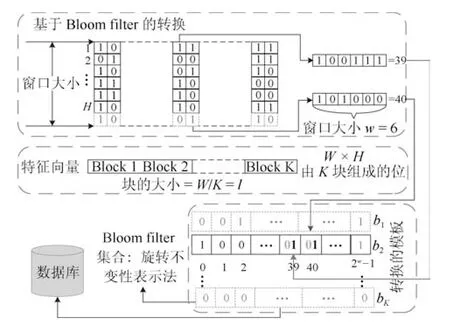
图2 Bloom filter 转换概述图[13]Fig.2 Overview of Bloom filter transformation[13]

Cappelli 等[16]提出了一种指纹细节点描述符(Minutia cylinder code,MCC).MCC 是将细节点集M={m1,m2,···,mn}转换成一组圆柱数据C={c1,c2,···,cn}的技术,其中每个m={x,y,θ},n 是提取的细节点的数量,圆柱是指在固定半径r 内记录中心细节点与其邻域细节点之间的方向(导向)和空间(位置)关系的数据结构.尽管MCC 具有较高的匹配性能,但可以从MCC 模板中获得原始细节点集[17],因此,文献[17] 提出了P-MCC (Protected minutia cylinder code)来保护MCC 模板.在P-MCC 方法中,通过单向转换函数B-KL 投影(B-KL projection)将MCC 模板C={c1,c2,···,cn}转换为P-MCC 模板V={v1,v2,···,vn}[17].B-KL 投影概述如下:1)在训练过程中,从MCC 模板计算出一个平均向量和k个最大特征值Φ;2)使用参数和Φk,在MCC 模板上执行KL 投影以生成2P-MCC 模板;3)使用单位阶跃函数对2P-MCC 进行二值化.尽管P-MCC生成了不可逆的实例,保证了MCC 模板的安全性,但P-MCC 的用户无法使用相同的指纹来重新发布P-MCC 模板.针对可撤销性问题,提出了2P-MCC(Two-factor protected minutia cylinder code).在2P-MCC 中,使用用户特定的密钥sss 对在P-MCC模板进行部分置换,生成2P-MCC 模板[18].然而,2P-MCC 方案不能推广到其他生物特征模式,因为它是专门为点集数据结构(即MCC 模板)设计的.

Ouda 等[19]提出了无标记的可撤销生物特征识别方法,即“BioEncoding”,来保护IrisCode.BioEncoding 方法中的两个基本输入是:n 位二进制向量c(生物特征数据)和随机生成密钥S ∈[0,1]2m-1,其中m 是系统参数.从两个输入导出BioCodeb∈[0,1]n/m的过程是:1)将c分割成具有m 位的多个块;2)将这些块转换成一组整数值x={x1,x2,···,xn/m};3)通过执行布尔函数f(x)将整数值转换为二进制值,该函数定义式为

其中,S[xi] 表示S 中的第xi个二进制,i=1,···,n/m.因此,输出二进制值形式的BioCodeb用于匹配.虽然文献[19] 表明S 可以作为公共信息存储在数据库中,但如果S 泄露,原始生物特征模板可以恢复.

表1 总结了各种可撤销的生物特征认证方案在转换方式、相似性和缺点方面的比较结果.

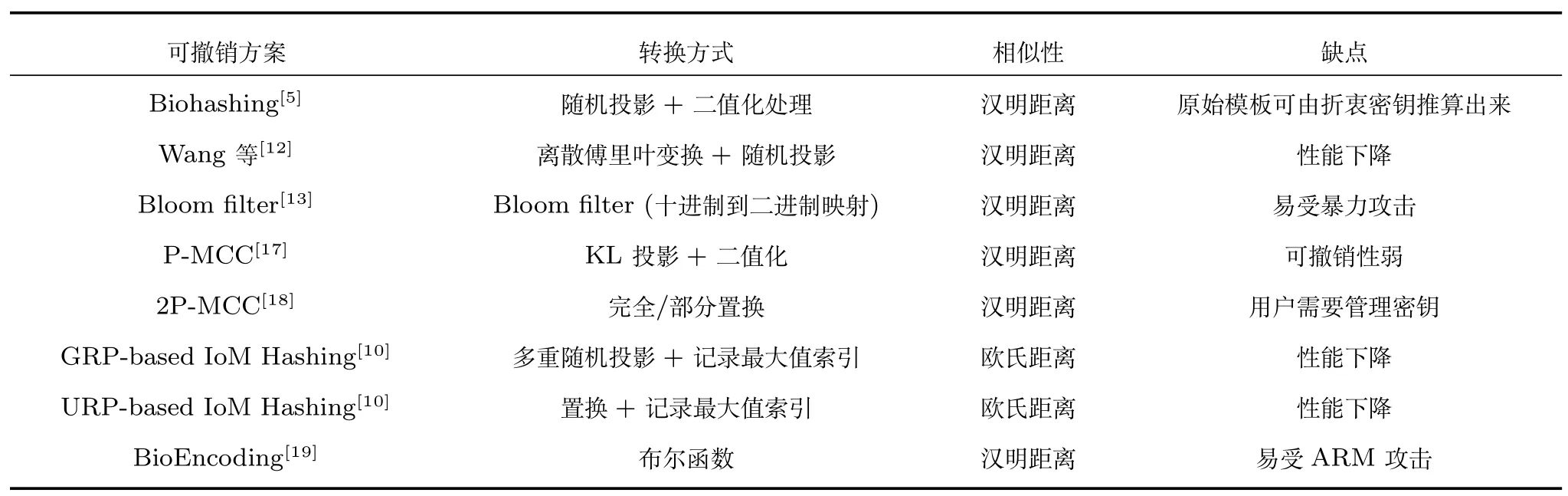
表1 各种生物特征模板保护算法的比较结果Table 1 Comparative result of various biometric template protection methods

在认证阶段,双因子可撤销生物认证方法依赖于其他认证因素,在转换过程中需要用户特定的令牌,转换过程复杂,且需要大量的存储空间存放额外的令牌化随机数据.单因子可撤销生物认证方法不依赖于其他独立的认证因素,在不影响性能精度的前提下,满足了不可逆性、可撤销性和不可链接性的要求,且转换过程简单,所需存储空间降低.两者的应用场景都是身份认证,但是单因子方法只需个人生物特征,而双因子方法还需要令牌.

另外,尽管双因子可撤销生物认证方法是生物特征模板保护的主要方法,但这种方法还是存在不足,例如,该方法需要用户的额外输入,而且外部因素可能遗忘,被盗或丢失,这导致了文献[6] 中被盗令牌场景的不利情况.被盗令牌场景是指真实用户的令牌(参数)受到攻击并被攻击者利用以发起零努力错误接受攻击的事件.此外,用户公开特定参数可能会产生转换模板入侵的风险,特别是对于生物特征加盐法的方案.单因子可撤销生物认证方法可以有效避免这些不足.

2 一种单因子的可撤销生物认证方法

2.1 方法框架

局部敏感哈希(Locality sensitive Hashing,LSH)主要通过将原始数据投影到更少数量的“桶”(buckets)来降低高维数据的维度.LSH 的目标是以最大的概率将类似的物体映射到相同的“桶”中[10].

定义1.LSH 是一族哈希函数H={hi:Rd→B},将数据点从Rd映射到“桶”b ∈B,并且任何两个给定点X,Y ∈Rd满足的条件:

其中,δ ＞γ,s(·)是相似函数.LSH 确保具有高相似性的数据点X和Y 在在经过哈希函数后有较高的哈希碰撞概率,即将X和Y 映射到同一个“桶”中;相反,彼此相似度低的数据点发生哈希碰撞概率较低,即两个数据点映射到不同的“桶”中.

双因子的可撤销生物特征认证方法将令牌化随机数作为外部因子带来一些问题,本文针对这些问题提出一种单因子的可撤销生物特征认证方法,即滑动提取窗口哈希(Window sliding and extracting Hashing)算法,简称WSE 哈希算法.该方法实际上应用了LSH 的理论,在本文指纹匹配的场景中,通过复制原始特征向量,尽可能增加有用特征的提取数量,经过哈希(滑动窗口跳位取值)后,相似物体的哈希值碰撞的几率一定也高,所以匹配成功.与文献[7] 中方法相比,该方法改进了滑动窗口取值与哈希函数模块,目的是提取更多有用的特征向量,增强不可逆性,以提高可撤销模板的性能和安全性.本文提出的单因子的可撤销生物特征认证方法框架如图3 所示,该方法只需要生物特征(以指纹为例)作为唯一的输入因子,与二进制随机数生成器生成的密钥r做运算生成可撤销的模板.具体来说,在注册阶段,首先由二值生物特征向量x生成置换种子(Permutation seed),然后置换密钥r,得到可撤销模板w.该阶段存储编码随机二进制向量v(密文)和模板w.在验证阶段,从密文中解码和置换密钥生成用于匹配的查询向量w′,其中置换种子由查询生物特征确定.最后w和w′,进行匹配,判断是否匹配成功.

图3 单因子可撤销生物特征认证方法框架Fig.3 Overview of the one-factor cancellable biometrics scheme

2.2 滑动提取窗口哈希算法

设x∈[0,1]l是一个具有长度l 的二元生物特征向量,则WSE 哈希算法的实现描述如下:

1)将x∈[0,1]l复制m 倍,形成扩展的特征向量∈[0,1]lm,其中m 是系统参数;该步骤增加了二元生物特征向量的长度,为接下来的精度要求和安全性分析做准备.

5)设r∈[0,1]lm是用户/应用程序特有的随机字符串,作为密钥key,它是由伪随机二进制数发生器生成的向量,将置换种子y作为r ∈r的索引置换y生成可撤销的模板w,w=[ry1,···,rylm] ∈[0,1]lm.算法1 展示了滑动提取窗口哈希算法.

算法1.滑动提取窗口(WSE)哈希算法

如图4 所示,以长度l=6 的二元生物特征向量,复制倍数m=2,窗口大小k=2 为例,演示步骤1～4,通过WSE 哈希算法生成置换种子y=[1,12]12的过程.

图4 WSE 哈希算法生成置换种子示意图(l=6,m=2,k=2)Fig.4 Diagram of generated permutation seed by WSE Hashing algorithm (l=6,m=2,k=2)

本文提出的一种单因子可撤销生物特征方案中的WSE 哈希算法流程图如图5 所示.在注册阶段,输入用户的生物特征向量x,x∈[0,1]l,与密钥r经过WSE 哈希算法,生成扩展向量和隐藏了真实信息的整数向量y=[1,lm]lm,y为置换种子.然后,将与r进行异或生成二进制编码的随机向量v,将y作为r的索引,并置换r生成可撤销的生物特征模板w,w=[ry1,···,rylm] ∈[0,1]lm,可以简写为w=Py(r),其中P()是置换函数.最后只将v和w存储在数据库中,这样做有助于保护用户的真实信息,增强不可逆性,提高安全性.一方面,因为r和都未保存,攻击者不能从v中轻易的得到r,必须同时猜测x(或)和r(从v中推出),另一方面,w是由真正的用户x(或)解码生成的,要得到正确的w必须是正确的生物特征输入.

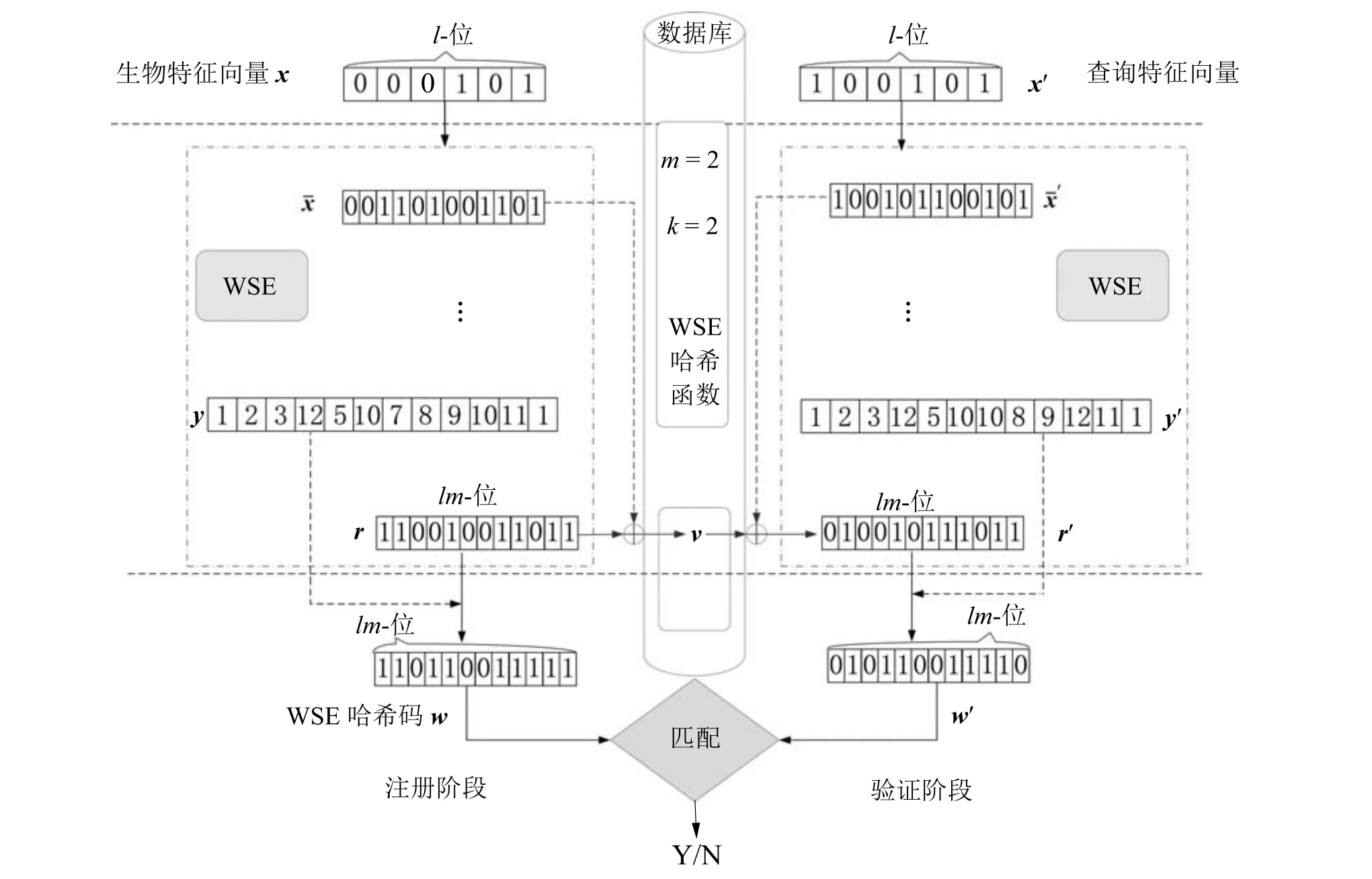
图5 WSE 哈希算法流程图(l=6,m=2,k=2)Fig.5 The flowchart of WSE Hashing algorithm (l=6,m=2,k=2)

在验证阶段,给出查询二进制生物特征向量x′,让其也经过WSE 哈希算法,得到扩展向量给定v,通过逆运算得到r′,然后置换r′,w′=Py′(r′)获得查询可撤销模板w′,换而言之,r′是由数据库中的v解码得到的.

该方案是单因子的,在验证阶段身份检验的唯一输入是生物特征,而不是像基于双因子的置换方案那样由第二个因子计算得出[20].在双因子方案中,如果在注册期间和验证期间的置换种子是相同的,则r置换前后的性能将被精确保留.然而,在本文提出的方法中,因为两种置换种子都来自于唯一的注册生物特征和查询生物特征,注册生物特征和查询生物特征在实际中是不相同的.这一点可以类比对称加密系统(见第4.3 节),r可以根据需要进行撤销和替换.

3 性能分析

3.1 实验环境

本文实验均在MATLAB R2017b 上运行,运行环境为Intel® Core(TM)i5-7500 CPU @3.40 GHz,Intel® HD Graphics 630 (1 024 MB),内存16.00 GB 的台式电脑.

本文用长度为256 位的二进制指纹向量x作为输入[8],在4 个公共指纹数据集(FVC2002 (DB1,DB2)[21]FVC2004 (DB1,DB2)[22])上进行实验.每个数据集包含100 个手指的采样图像,相当于100 个用户,每个手指采样8 次,得到有8 个样本,因此总计有800 个指纹图像样本.因为文献[8] 是基于学习的方法,所以每个用户的8 个样本中有3个用于训练,有5 个样本可以用于测试.通过比较汉明距离获得匹配结果,因为注册和查询标识符均是二进制向量.

本文中,评价指纹识别系统性能准确性的参数是真/假匹配得分(Genuine/Imposter matching score)和等错误率(Equal error rate,EER).评价标准是文献[23] 中的测试协议.在每个数据集中,可以生成真匹配得分1 000 个假匹配得分4 950 个为了无偏差地评估所提出的方案,本文基于五个不同密钥key (r)的实验来计算平均EER.该方案是单因子可撤销方案,因此不需要对盗令牌的场景进行评估.

文中处理时间是指注册阶段和验证阶段的总计,其中前者包括密钥key(r)生成,可撤销模板生成和密钥编码;而后者包括密钥解码,查询可撤销模板生成和匹配.表2 说明了当m=1 000和k=3 的WSE 哈希算法处理时间.从表2 中可以看出,WSE哈希算法两个阶段的平均处理时间约等于0.035 s.

表2 WSE 哈希处理效率(s)(m=1 000,k=3)Table 2 Processing efficiency of WSE Hashing (s)(m=1 000,k=3)

3.2 认证性能

本节分析内部各个参数的不同取值对认证性能(EER)的影响,以及比较对比实验和本文方法的认证性能.

3.2.1 各个参数对认证性能的影响

方案中有两个系统参数,分别是扩大的倍数m(m ≥1)和窗口大小k (k ≥2).本节通过实验来分析m和k 对所提方法的认证性能的影响,用等错误率EER(%)表示,EER 越低,说明性能越好.

图6 显示了WSE 哈希算法在数据库FVC2002 DB1 上的“EER-vs-k”的曲线,其中窗口大小k 从2,3,4 到5 的变化,而m 从1,5,10 到15 的变化.我们观察单个线条,m 值固定不变且k 变大时,EER (%)会变高.如算法1 中所述,k 表示子位块,因此当k 值增大时,需要附加更多的比特,增加了子比特块之间的噪声影响,所以EER (%)变高.图6的另一个观察结果是当m 变大时EER (%)变低.

根据图6 的观察,为了进一步研究m 对认证性能的影响,进行了如下实验研究.实验时,使用控制单一变量法,将k 固定为2,通过改变m 的取值来观察EER (%)的变化,m 的取值分别为1,5,10,15,20,40,100,200,500,800,1 000.图7 显示了FVC2002 DB1 上的“EER-vs-m”曲线.增大m 则EER 相对较低,认证性能提高;m 在1,5,10和20之间变化较明显,而认证性能在m (m ≥40)时以较慢的速度改变.值得注意的是,m 较大时可以减少由注册和查询生物特征生成的两个置换序列r与r′的冲突,但是m 也不能一味的增大,因为m 过大时,会造成资源浪费及攻击者易盗取的安全隐患.

图6 EER-vs-k 曲线图(FVC2002 DB1)Fig.6 Curves of“EER (%)-vs-k”(FVC2002 DB1)

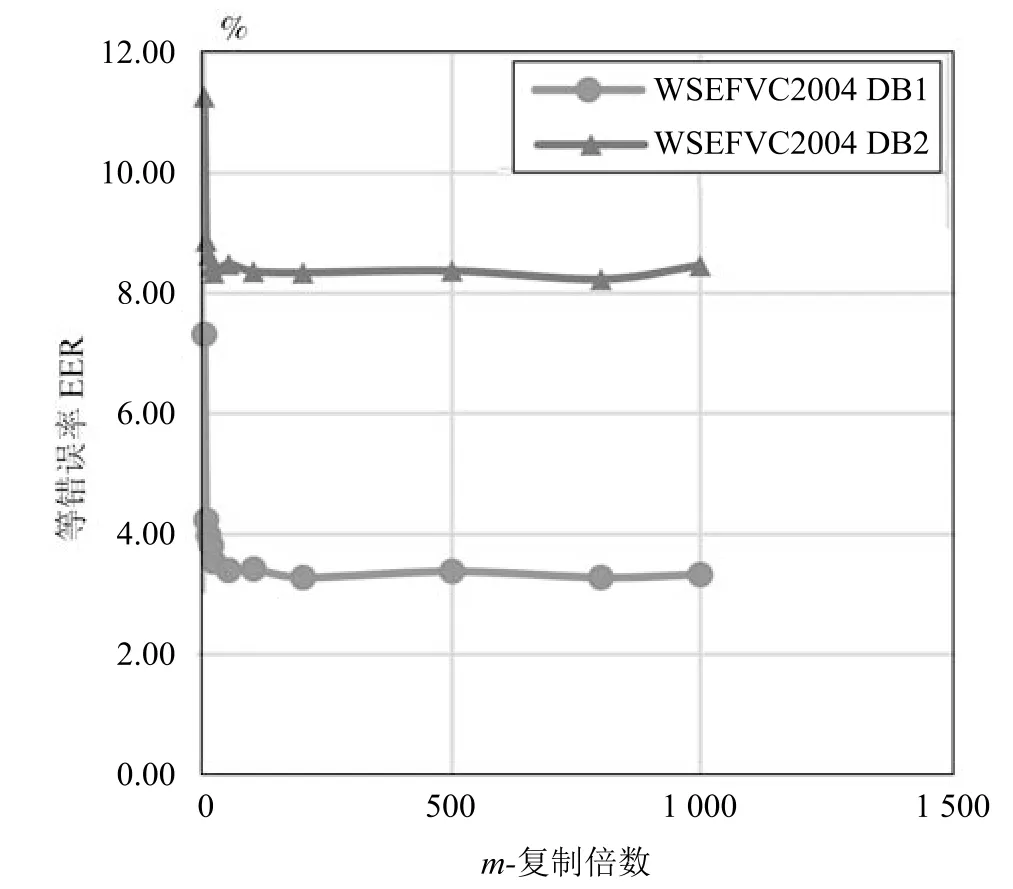
图7 EER-vs-m 曲线图(FVC2004 DB1/DB2)Fig.7 Curves of“EER (%)-vs-m”(FVC2004 DB1/DB2)

3.2.2 对比实验的认证性能

本文WSE 哈希算法在m=1 000和k=3时的性能精度与原始生物特征识别方法、4 种经典的双因子指纹可撤销生物识别技术以及文献[7] 的单因子方法EFV Hashing 比较,如表3 所示.据观察,WSE 哈希算法在数据库FVC2002 DB1和FVC2004 DB1 上等错误率EER 均最低,在其他数据库上也展现了良好的性能.除此之外,在与双因子方案比较中,WSE 哈希算法优于文献[18]、文献[24]和基于URP 的IoM[10].在与单因子方案EFV哈希算法[7]的比较中,由于WSE 哈希算法改进了滑动窗口取值与哈希函数模块,在4 个数据库上性能精度均有所提升,且不可链接性也有提升(参见第3.5 节).

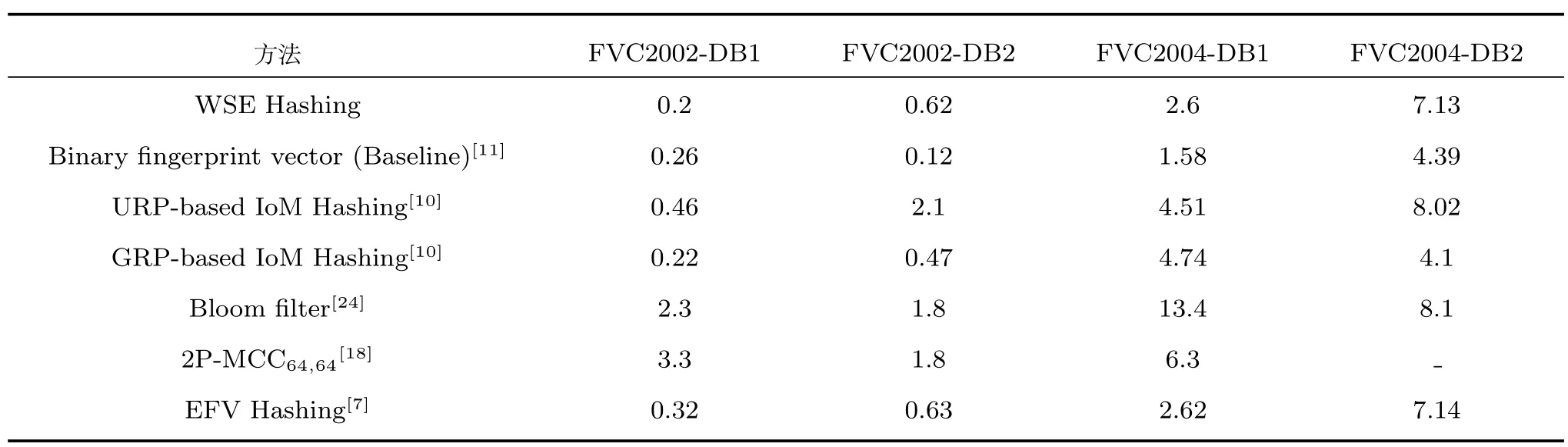
表3 不同方法的性能精度对比(EER)(%)Table 3 EER comparison between proposed method and other methods (%)

3.3 不可逆性

本文方法在数据库中存储的只有v和w,若能逆推出x或则说明不满足不可逆性.假设攻击者已经盗取v,根据v=r⊕,我们如果知道r或都可以经过逆运算得到另外一个,但是由于r和在数据库中均未存储,所以无法恢复或r.

假设攻击者盗取了w,即使已知w=Py(r),但由于x未存储不可知,所以置换种子y不可知,则从w中恢复密钥r的枚举次数是2lm次,并且l=256,m=1 000,这在实际计算中也是不可行的,因而无法恢复x或.

3.4 可撤销性

根据可撤销性的要求,一旦模板被破坏,就应该生成一个新的模板并替换受损模板.为了验证方案的可撤销性,计算和评价了来自每个数据集真匹配得分(Genuine match score)、假匹配得分(Imposter match score)和配对真匹配得分(Matedgenuine match score)分布.计算Mated-genuine分数分布的步骤是:1)对于每个用户,使用51 个不同的r和用户的第一个特征向量生成51 个不同的模板;2)将第一个模板(假设为已泄露的模板)与其余50 个模板(假定为更新的模板)匹配,从而为每个用户生成50 个Mated-genuine 分数.因此,共有5 000 (50×100 个用户)Mated-genuine 得分.图8 显示了FVC2002 的DB1和DB2、FVC2002 的DB1和DB2 这4 个数据库的可撤销性分析,其中Mated-genuine和Imposter 得分分布在很大程度上重叠.这表示对于相同的用户,用不同的密钥r生成的模板彼此之间不能区分,所以WSE 哈希算法是满足可撤销性的.

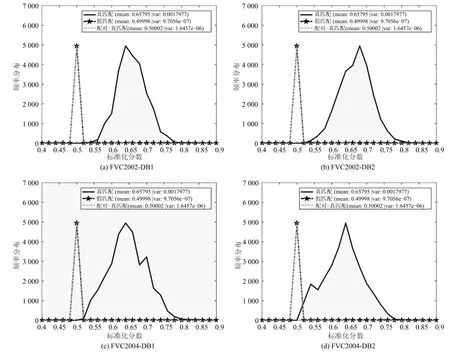
图8 可撤销性分析Fig.8 Revocability analysis

3.5 不可链接性

根据不可链接性的要求,同一个生物特征向量x或与不同的密钥rs 生成的多个模板ws,这些r之间不能链接.本文遵循文献[25] 的基准框架来验证WSE 哈希算法的不可链接性.方法如下:

1)计算WSE 哈希算法模板与配对/非配对样本得分分布(Mated/non-mated samples score distributions)的模型交叉匹配.其中,配对样本分数分布(Mated samples score distributions)是由同一用户通过不同密钥产生的模板之间的相似性匹配来计算.非配对样本得分分布(Non-mated samples score distributions)是指由不同用户利用相同密钥导出的模板之间的相似性匹配.

实验在所有数据集上进行了测试,其中最佳参数集为m=1 000,k=3.为了公平地评估转换模板的不可链接性,将ω 设置为1,并且ω 是计算和的参数.根据文献[25],ω=1 是不可链接性评估标准的最坏情况.

图9 显示了4 个数据库(FVC2002 (DB1,DB2),FVC2004 (DB1,DB2))的不可链接性的分析.正如图9 所示,配对和非配对样本的得分分布曲线是重叠的,这表示源自同一用户或不同用户的模板无法区分.因此,WSE 哈希算法满足不可链接性标准.

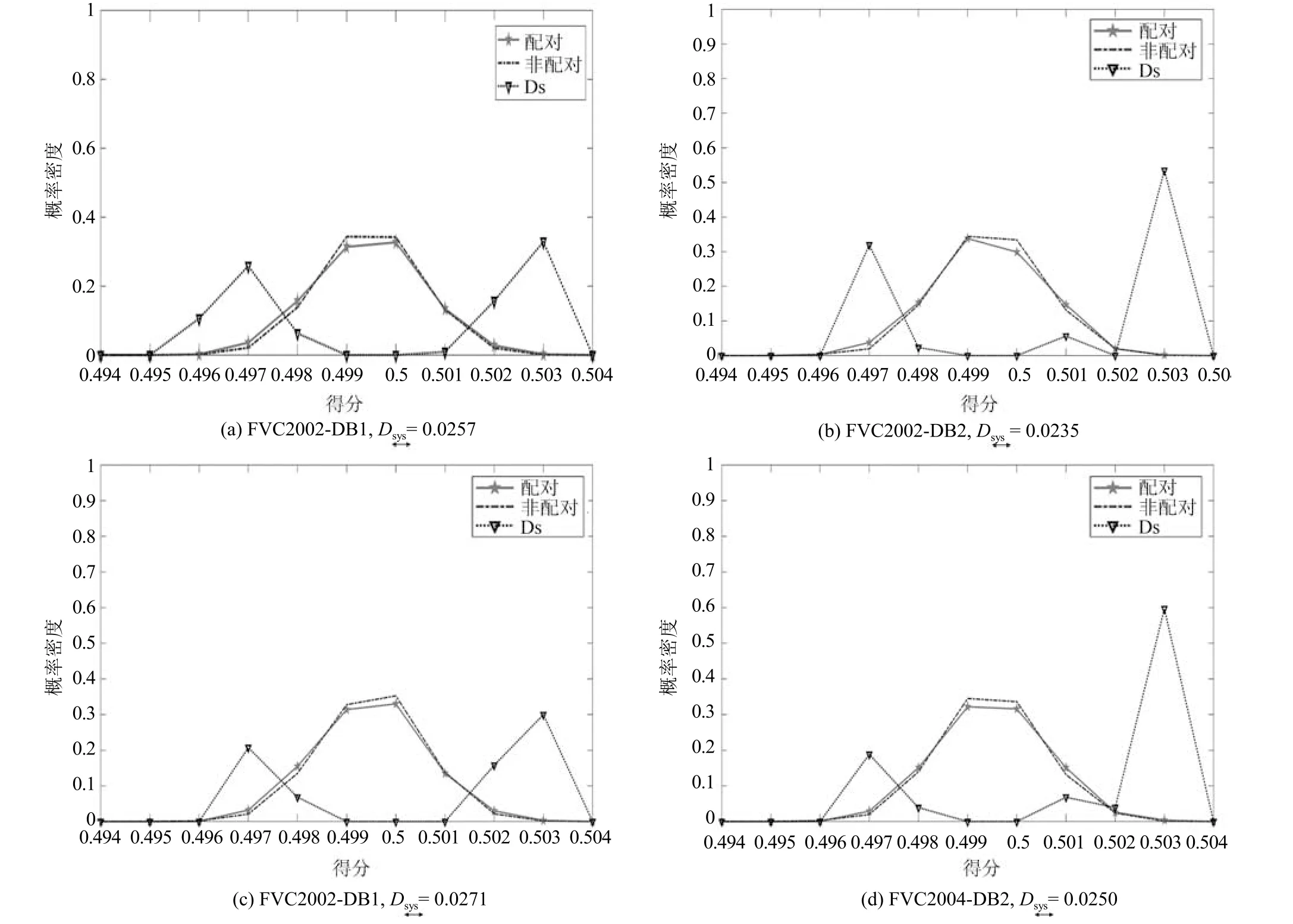
图9 不可链接性分析Fig.9 Unlinkability analysis

表4 列出了WSE 哈希算法和EFV 哈希算法[7]所有测试数据集的的详细值,表中WSE 哈希算法的最大值=0.03 (接近0),这表明WSE哈希算法接近完全不可链接的情况.并且我们可以观察到,EFV 哈希算法的最大值=0.05 ＞0.03,这说明WSE 哈希的不可链接性比EFV 哈希算法的不可链接性高,安全性和隐私性也高于EFV哈希算法.

表4 不可链接性的全局度量 (m=1000,k=3)Table 4 Globalmeasureof unlinkability(m=1 000,k=3)

表4 不可链接性的全局度量 (m=1000,k=3)Table 4 Globalmeasureof unlinkability(m=1 000,k=3)

4 安全性分析

本文是单因子的可撤销生物特征模板保护方法,所以基于双因子的可撤销生物特征模板保护中第2个因子的安全性问题,在这里将不再分析.在本节中,我们从暴力攻击、字典攻击和唯密文攻击3 个方面来分析本文方法的安全性.

4.1 暴力攻击

暴力攻击(Brute force attack)作为安全攻击的一个经典方法,指的是用穷举法试图随机使用非法访问生成转换的查询实例.在本文中,暴力攻击是通过猜测来衡量的WSE 哈希算法的复杂性在代码中耗尽了代码w′方式.由于w′是具有长度lm的二进制向量,因此需要总共2lm的猜测复杂度.本文实验设置m=1 000,l=256,其猜测复杂性为2256000.因此,暴力攻击对本文方法是不可行的.

4.2 字典攻击

与暴力攻击中对整个散列代码的盲目猜测不同,字典攻击(错误接受攻击)(False accept attack)需要更少的尝试来获得非法访问[26].实际上,基于阈值的决策方案通常应用于生物识别系统,因此这种攻击是可行的.换句话说,只要匹配分数超过预定阈值τ,就可以授予访问权限,这可以显著减少攻击的次数.

选择FVC2002 DB1 作为评估实例.令参数m=1 000,k=3和l=256,实验结果如图10 所示,阈值τ=0.56.这说明字典攻击需要的密码序列的最小匹配是lmτ=143 360.因此,字典攻击复杂度为2lmτ=2143360.尽管比暴力攻击小得多,但是在现实操作中也是不可行的.

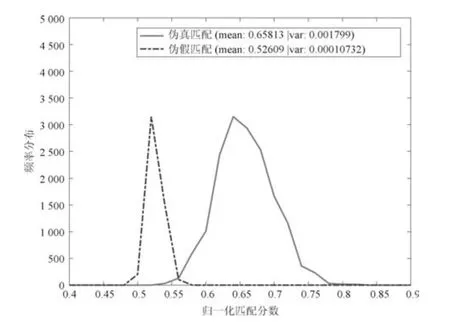
图10 真匹配—假匹配曲线(FVC2002 DB1,m=1 000,k=3)Fig.10 Genuine-imposter curve on FVC2002 DB1(m=1 000,k=3)

4.3 唯密文攻击

从另外一个角度看,本文提出的WSE 哈希算法可以看作是一种特殊的对称加密[4].对称加密(也称私钥加密)是指加密和解密使用相同密钥(或是两个密钥之间可以进行简单的转换)的加密算法.在本文方法中,生物特征信息x(或)对应于对称加密系统中的明文,随机的二进制向量r/r′对应于加密/解密密钥,v对应于密文.因此,我们还可以考虑针对对称加密算法的安全攻击,如唯密文攻击(Cipher-text only attack,COA).

唯密文攻击(COA)是指攻击者仅仅知道密文,来得到相应的明文信息.在文中,密文对应于存储在数据库中的v,若已知v,攻击者可以用2l种可能的组合来枚举x(或者在第3.1 节,猜测正确x的平均时间是s,其中0.035 s 是验证所花费的平均时间.在本文中,l=256,因此这需要平均year 来猜测正确的x.这表明猜测x是计算不可行的.另一方面,虽然w=Py(r),如果x(来源于生物特征的置换种子)未知,则从w中恢复r同样在计算上是不可行的,因为r的暴力攻击猜测是2lm个组合.

5 总结与展望

双因子可撤销的生物特征认证方法引入额外因子即令牌化因子带来了隐私和安全威胁问题.本文提出了一种单因子可撤销生物识别解决方法,即WSE 哈希算法.针对这一问题,本文提出了一种唯一二值数据生物特征作为输入因子的单因子可撤销生物识别方法,即WSE 哈希算法.WSE 哈希算法满足不可逆性,可撤销性,不可链接性以及精确性这4 个可撤销的生物特征模板保护标准,也抵御了3 种方式的安全性攻击测试.同时WSE 哈希算法也可以扩展到二值向量形式表示的虹膜、面部特征、掌纹和静脉等生物特征识别.另外,算法的安全性,如碰撞攻击、差分攻击等攻击方式,也是我们未来研究方向.