三层无标度关联网络协同传播模型阈值研究
徐云程,胡 华,孙小军
(1.宁夏大学数学统计学院,银川 750021;2.宝鸡文理学院数学与信息科学学院,陕西 宝鸡 721013)
0 引言

其中

1 三层无标度关联网络协同传播模型
1.1 三层关联网络结构图
首先,我们建立一个三层关联网络结构图,整个系统由3个子网A,B,C构成,假设其分别含有N,M,H个节点。子网A到B、B到C之间有交叉连接,子网A到C之间没有连接,且子网之间的连接是随机的,记从A到B、B到A、B到C、C到B的层间网络分别为AB,BA,BC,CB。具有3个子网的关联网络结构图如图1所示。
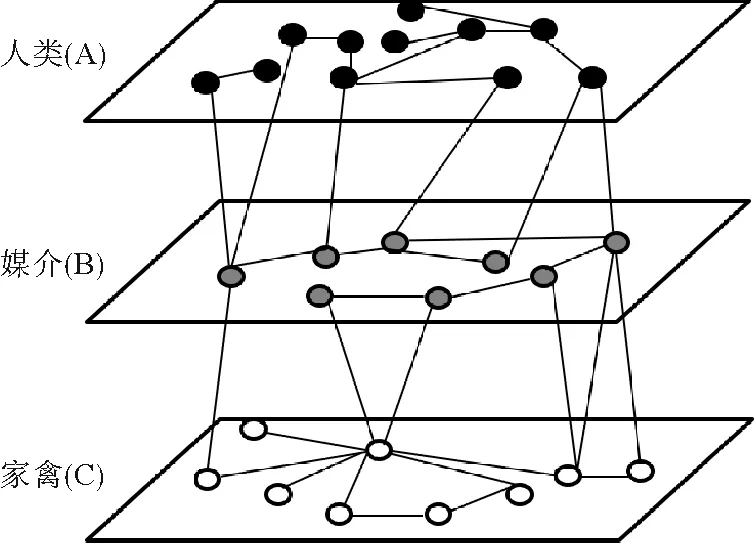
图1 三层关联网络
1.2 相关知识
在建立模型之前,对相关符号做以下说明(见表1)。

表1 三层关联网络符号说明

续表1
根据表1,可得3个子网A,B,C的易感节点总数、染病节点总数、节点总数分别为
联合度分布分别为
边界度分布分别为
平均度分别为
1.3 三层无标度关联网络协同传播模型
由于无标度网络给出的度分布信息是针对大部分节点的,并没有准确描述出单个节点的情况,因此,基于单个节点去研究无标度网络上流行病的动力学行为是很有现实意义的。本文用SIS仓室模型来描述3个子网上的动力学行为,在整个系统上,节点可以有两种状态:易感态(S)、感染态(I)。
接下来,对整个系统的动力学过程作如下假设:子网A中的一个易感节点通过一条层内连边被子网A中的一个染病节点感染的概率为λaa,通过一条层间连边被子网B中的一个染病节点感染的概率为λba,对于非相关性无标度网络,子网A中任意一条给定的边与子网A中一个染病节点相连的概率为
(1)
子网A中任意一条给定的边与子网B中一个染病节点相连的概率为
(2)
子网B中的一个易感节点通过一条层内连边被子网B中的一个染病节点感染的概率为λbb,通过一条层间连边被子网A(C)中的一个染病节点感染的概率为λab(λcb),子网B中任意一条给定的边与子网A中一个染病节点相连的概率为
(3)
子网B中任意一条给定的边与子网B中一个染病节点相连的概率为
(4)
子网B中任意一条给定的边与子网C中一个染病节点相连的概率为
(5)
子网C中的一个易感节点通过一条层内连边被子网C中的一个染病节点感染的概率为λcc,通过一条层间连边被子网B中的一个染病节点感染的概率为λbc,同样可定义子网C中任意一条给定的边与子网B中一个染病节点相连的概率为
(6)
子网C中任意一条给定的边与子网C中一个染病节点相连的概率为
(7)
同时,子网A、B、C中的染病节点也会分别以恢复率μa,μb,μc变为易感节点。
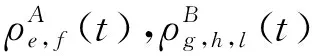
(8)
其中,e=0,1,…,naa;f=0,1,…,nba;g=0,1,…,nab;h=0,1,…,nbb;l=0,1,…,ncb;u=0,1,…,nbc;v=0,1,…,ncc。
2 阈值分析
2.1 全局传播阈值
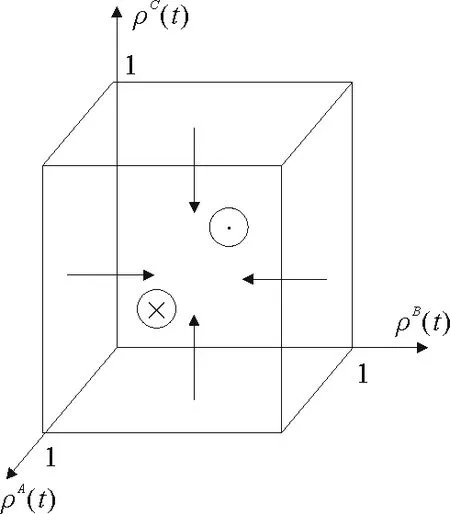
图2 感染规模运动方向图
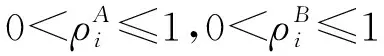
(9)
方程(9)表示整个系统已经进入了稳定状态,所以λaa,λbb,λcc将非常逼近λd,故可以用λd替换λaa,λbb,λcc,得:
(10)
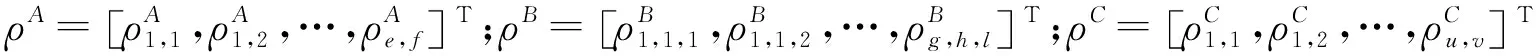
(11)
基于式(11)将式(10)改写为矩阵形式,有
(12)
即
(13)
令
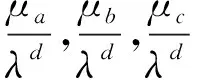
2.2 孤立子网的传播阈值
考虑各孤立子网上的情况,即仅考虑层内传播,不考虑层间传播。孤立子网A,B,C的动力学模型分别为
(14)
在稳定状态,基于式(11)将上述模型写为矩阵形式有
(15)
(16)
其中,Λmax(DA),Λmax(DB),Λmax(DC)分别为孤立子网A,B,C对应的邻接矩阵DA,DB,DC的最大特征值。
2.3 结论
为对比异质网络耦合的三层串状关联网络的全局传播阈值与各孤立子网传播阈值的大小关系,这里将分两种情形进行讨论。
1)各孤立子网的恢复率均相等,即μa=μb=μc。
引理1(柯西交错定理)[15]设H是一个n×n的对称矩阵,而M是H的一个n-1主子阵,如果λ1≥λ2≥…≥λn和μ1≥μ2≥…≥μn-1分别是矩阵H和M的特征值,那么λ1≥μ1≥λ2≥…≥λn-1≥μn-1≥λn。

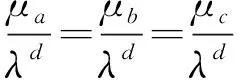
Λmax(P)≥Λmax(DA),Λmax(P)≥Λmax(DB),Λmax(P)≥Λmax(DC),
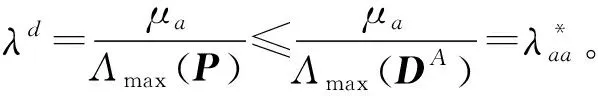
2)各孤立子网的恢复率至少有两个不相等,即μa,μb,μc中至少有两个不相等。
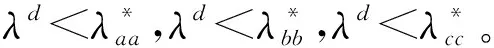
证明:由式(12)有
λdDAρA+DBAρB-μaIρA=0
DABρA+λdDBρB+DCBρC-μbIρB=0
DBCρB+λdDCρC-μcIρC=0
(17)
基于扰动理论对各孤立子网的阈值进行研究,对传播阈值及感染密度施加扰动(18):
(18)
将式(18)代入式(17),同时忽略二阶项,有:
(19)
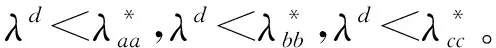
3 数值仿真
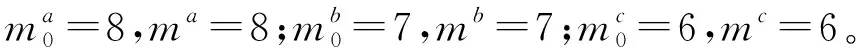
图3和图4分别展示了关联网络及对应孤立网络平均最终感染规模的三维切平面等高线图,两幅图中最外侧两条曲线之间的区域代表疾病消亡,其余部分代表疾病变成了地方病将在人群中永远流行。显然图3最外侧两条曲线之间区域的面积比图4小,故关联网络全局阈值比孤立网络阈值要小[16],即协同传播减小了传播阈值,促进了疾病的传播。
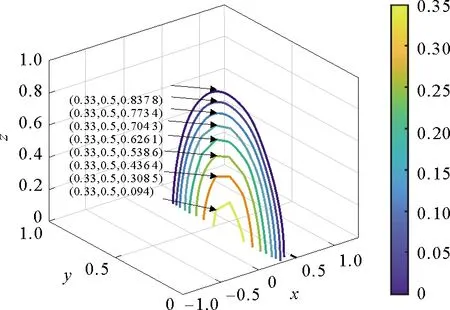
图3 关联网络平均最终感染规模
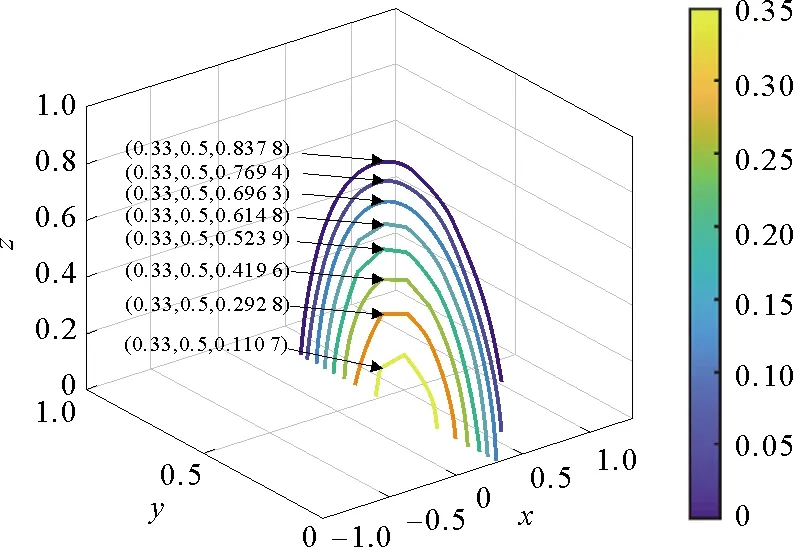
图4 孤立网络平均最终感染规模
4 结论
本文基于异质平均场理论构建了三层无标度关联网络协同传播模型,利用扰动理论对比分析了各子网的传播阈值与全局阈值的相对大小。通过严格的数理方法分析得到:对三层无标度关联网络上的协同传播而言,当各子网的恢复率均相等时,全局传播阈值小于等于单个子网的传播阈值;当各子网的恢复率至少有两个不相等时,全局传播阈值只能小于单个子网的传播阈值。总之,协同传播会使阈值减小,也即协同传播促进了疾病的传播。
文中所建模型不仅可以分析部分媒介传染病的传播,还可以用来分析艾滋病在男人、女人和儿童之间的传播。所得结论有助于理解媒介传染病的传播机理、解释某些流行病快速威胁人类的原因,且理论结果将为卫生部门更好地控制和预防流行病提供科学依据。事实上,在现实生活中也存在部分能在人与家禽之间传播的媒介传染病,同时,媒体报道在疾病的预防和控制中也发挥着至关重要的作用,下一步将对受媒体报道影响的三层环状无标度关联网络协同传播模型进行研究。

