带有丢包的分布式网络系统的滚动时域融合估计策略
范建明,薛斌强
(青岛大学自动化学院,山东 青岛 266071)
0 引言


然而,上述MHE方法在计算中只考虑了估计的准确性,计算过程复杂,当计算量过大时会降低估计效率。所以本文针对含有丢包的网络系统提出了一种分布式滚动时域估计(Distributed Moving Horizon Estimation,DMHE)方法,不仅给出了丢包补偿策略,还利用标量加权线性最小方差的方法在保证了估计的准确度的同时减少了计算过程。最后对该估计算法的稳定性进行了详细分析并通过仿真验证了该方法的有效性和合理性。
1 问题描述
考虑式(1)的线性离散的随机丢包系统状态空间方程:
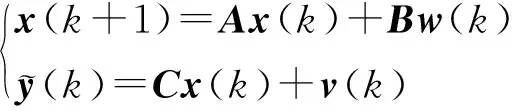
(1)
x(k)∈X,w(k)∈W,v(k)∈V
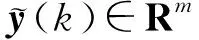
(2)
其中,δjk是符号函数,E{·}表示期望,Q≥0,R>0,Q和R反映了系统对模型和测量结果的置信度,如果Q>R,则表示系统模型对估计效果的影响大于测量值;反之亦然。
当系统发生丢包时,采取测量补偿的方法,利用零阶保持器将上一时刻的测量值作为当前时刻的测量值,可以将带有丢包的系统描述为
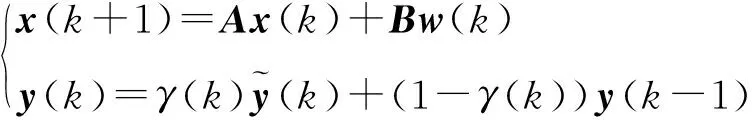
(3)
其中,γ(k)表示测量值丢失情况,并满足在0与1之间取值的Bernoulli分布。γ(k)=1时表示该时刻系统无丢包现象;当γ(k)=0时测量值丢失,估计器保持前一时刻的数据,丢包概率满足
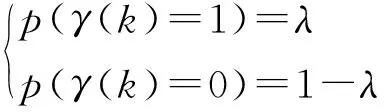
(4)
假设k时刻我们得知数据包是否发生丢失,也就是说γ(k)已知(可以通过比较y(k)与y(k-1)的值得到γ(k))。
2 估计器的设计
2.1 性能指标的选取
假设系统有L个传感器,每个传感器能够实现本地的数据估计以及与相邻传感器进行数据传输和交换。基于MHE的滚动优化策略,首先考虑一个长度为N+1的滚动窗口,并且窗口中的测量数据均由第i个传感器节点得到。根据MHE原理,在T时刻,节点i的状态估计值可以通过极小化一个二次优化目标函数(5)得到。
(5)
s.t.式(1)~式(4)。
(6)
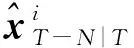
(7)
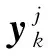
(8)
此时,到达代价函数的形式可以描述为
(9)
且满足
β1+β2+…+βL=1
(10)
2.2 加权矩阵的计算
从目标函数中可以看出,该方法在估计分布式系统的状态时利用从相邻节点得到的测量值和先验估计值来补偿本节点的估计效果,其中到达代价函数部分采用了加权融合的策略,但是加权矩阵的计算方法没有最优性,因此在设计时考虑到估计的实时性,采用了计算量小的按标量加权线性最小方差的融合准则。
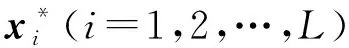
(11)
(12)
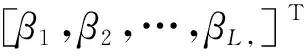
(13)
并且trP≤trPii。
由引理1可知,在T时刻,当得知系统状态的L个无偏估计值时,通过计算得到各个传感器估计值的加权矩阵并最终获得最优的融合估计值。但值得注意的是,本文在求解T时刻的估计值时,是对到达代价函数进行加权计算并通过求解一个目标函数直接获得最终估计值,所以不能直接使用引理1中的公式,因此本文提出了一种策略,即将T-1时刻对T时刻的状态估计值作为加权矩阵的计算标准。
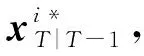
(14)
在互协方差矩阵Pij已知的情况下,将式(14)带入式(12)即可得到T时刻的加权矩阵。其中Pij可以是根据每个节点性质设定的固定矩阵,也可以是每个估计时刻通过计算得到的时变矩阵,具体计算方法可参考文献[9]。
3 估计器稳定性分析
接下来以节点i为例分析估计器的稳定性,为书写方便,证明过程中下标ek|T均记为ek。
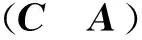
(15)
s.t.式(1)~式(4)。
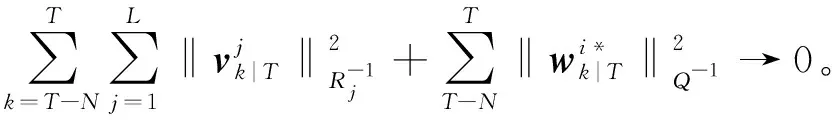
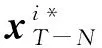
证明:对估计误差求期望可得
(16)
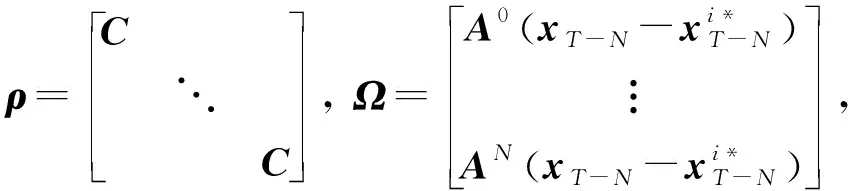
(17)
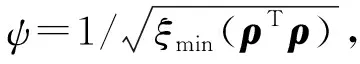
(18)
显然
(19)
对其两侧求期望得
(20)
结合式(16)和(21)可得
(21)
由式(2)得v(k)和w(k)的均值为零,所以化简得
(22)

4 仿真分析
为进一步验证所设计估计方法的有效性,需要进行仿真分析,为此考虑以下状态空间模型:
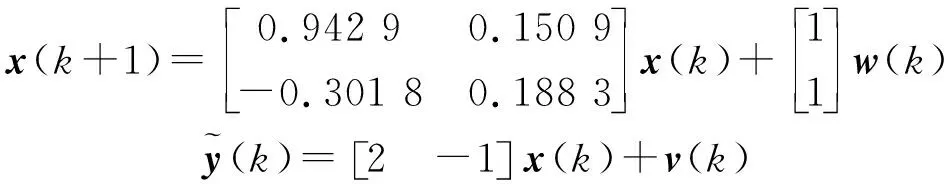
(23)
将系统的平均误差范数(MEN)表示为
(24)
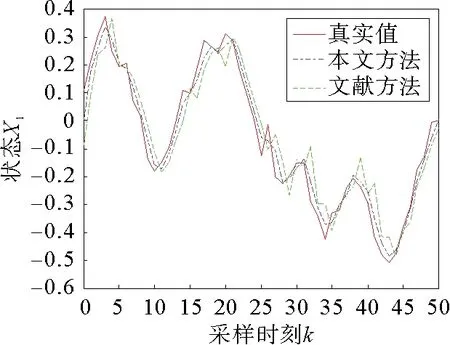
图1 λ=0.8时状态x1
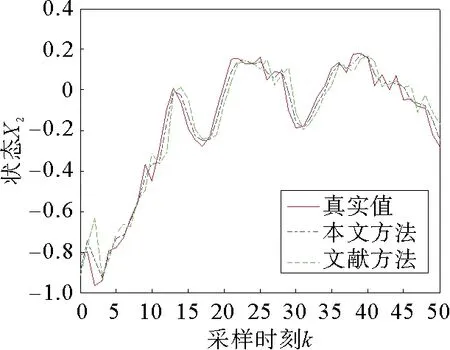
图2 λ=0.8时状态x2
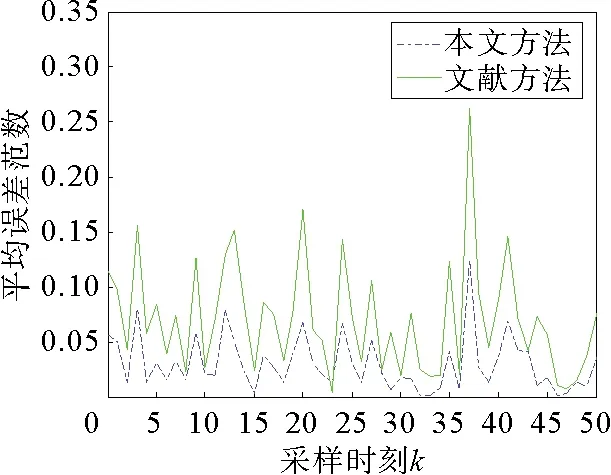
图3 λ=0.8时MEN
图1~图3给出了给定丢包概率下的状态轨迹,从图中可以看出,DMHE算法由于考虑了丢包补偿策略,所以估计状态的跟随效果较好;并且从表1得知,随着丢包概率的增加,DMHE相对于参考文献中的算法能够得到更小的估计误差。表2给出了计算量不同时估计所用的时间,从中可以看出DMHE所采用的按标量加权线性最小方差的融合准则能够在保证估计效果的情况下减少估计时间,并且效果随着计算量的增加而更加显著。

表1 不同λ下的MEN

表2 不同k下的估计用时(s)
5 结论
针对具有随机丢包的分布式网络系统的状态估计问题,提出了一种鲁棒滚动时域估计方法。系统中的节点能够通过网络与相邻节点传输数据,并采用零阶保持器来补偿丢包对估计的影响。基于滚动优化原理,传感器节点利用本地测量数据和相邻节点传来的数据将状态估计问题转化为固定窗口内的二次优化问题,并使用标量加权线性最小方差的方法对性能指标进行加权融合。该方法不仅保证了系统的一致性,还在保证准确度的情况下减少了计算时间。最后,讨论了估计器的稳定性并进行仿真验证。

