2D-C/SiC复合材料面内剪切强度分布研究

吴亚波， 王波， 王新军， 李辉， 陈果， 李丽娟， 米雪

（1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都610213；2.西北工业大学 航空学院，西安710129）

0 引言

碳纤维增强碳化硅陶瓷基(C/SiC)复合材料不仅克服了陶瓷材料脆性断裂的缺点，还具备低密度、耐热性高等优越性能，在航天航空等国防工业尖端领域被视为最理想的备选材料[1-2]，如高推重比航空发动机的新一代热结构材料等。随着C/SiC复合材料的应用不断推进，材料尺寸不断增大，工作环境越发复杂，剪切应力对C/SiC复合材料的力学性能、损伤进程及失效模式都存在显著的影响，因此研究材料的剪切性能就显得十分必要。由于制备工艺等原因，材料细观缺陷和宏观性能分散性有直接关系[3]，所以确定C/SiC复合材料的面内剪切强度分布规律对材料性能的研究和应用具有重要的工程意义。大多数研究表明，双参数Weibull分布可以较好地模拟陶瓷基复合材料的强度分布[4-7]。国内主要针对陶瓷基复合材料拉伸和弯曲性能的分布规律进行了相关研究[8-12]，面内剪切性能分布规律的研究报道较少[13]。国外一些专家学者关于强度分布的研究不仅仅局限于陶瓷基，对复合材料强度的统计分布特性进行了全面系统研究，建立了准脆性材料的强度概率分布模型，研究了陶瓷基微复合材料的拉伸强度分布规律[14-16]。

本文对2D-C/SiC复合材料的面内剪切强度性能进行统计特性研究。以双参数Weibull分布为模型，对实验数据进行参数估计和假设检验，确定了2D-C/SiC复合材料面内剪切强度分布规律，分析对比了分布函数获得的强度预测值与实测值，研究了2D-C/SiC复合材料面内剪切强度分布。

1 实验和试件

2D-C/SiC复合材料的制备工艺采用化学气相渗透（CVI）法。最终得到试件纤维体积含量约为40%，密度约为2.0 g/cm3，孔隙率约为19.5%。试件尺寸如图1所示，试件厚度约4 mm，最窄净截面宽度约为12 mm。依照ASTM C1292-00试验标准进行面内剪切试验。

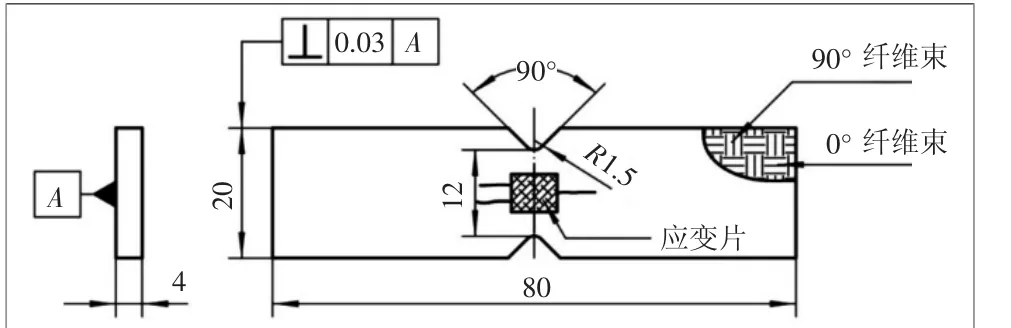
图1 面内剪切试件

2 结果与分析

2D-C/SiC复合材料面内剪切强度分布规律研究的数学原理为数理统计中的非参数检验。主要步骤为：首先进行概率分布的参数估计；然后对概率分布进行假设检验。

2.1 统计分析方法

复合材料的断裂强度、弯曲强度服从双参数Weibull分布[9]，因此采用双参数Weibull分布进行2D-C/SiC复合材料面内剪切强度分布特性研究。双参数Weibull分布表达式为

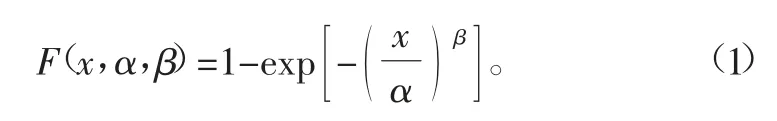
式中：α为Weibull分布的尺度参数；β为形状参数，也称为Weibull模数，可以作为衡量数据分散性的指标，数值越大代表强度分散性越小，面内剪切强度性能越稳定。

经验失效概率S代替F(x，α，β)。将实验数据按由小到大排序，并依次记为S1，S2…S30，S代表在一定应力水平下失效的经验概率，定义如下[3,8]：

2.2 参数估计

采用线性回归法进行双参数Weibull分布参数估计，将式（1）中双参数Weibull分布函数等式两边同时取对数，得到一个Y=BX+A形式的线性函数等式，经过数学运算之后的分布函数为

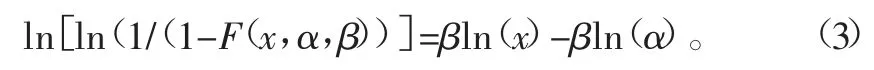
这样，双参数Weibull分布函数的参数就与线性函数的斜率和截距联系起来，只要通过线性拟合得到线性函数的斜率和截距，就可以解出双参数Weibull分布的估计参数，具体对应关系如表1所示。

表1 双参数Weibull分布的估计参数

以（X，Y）=（ln（xi），ln［ln（1/（1-Si））］）为数据对，绘制散点图，利用Origin软件对散点进行线性拟合，线性拟合结果如图2所示。由拟合结果可见，线性函数斜率为15.56，截距为-71.44，根据表1中的数学关系，可得双参数Weibull分布的尺度参数α=98.62，Weibull 模 数β =15.56。至此已经完成双参数Weibull分布参数估计，进而可以得到2D-C/SiC复合材料面内剪切强度分布函数为

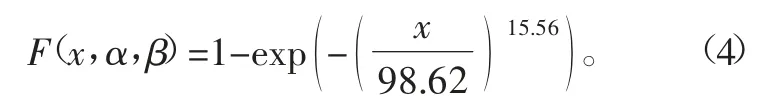
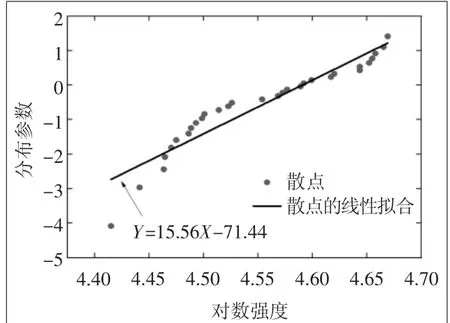
图2 线性回归法参数估计结果

2.3 假设检验

Kolmogorov是比较一个频率分布f(x)与理论分布F(x)或者2个观测值分布的检验方法。假设从一个连续分布函数F(x)中取样(X1，X2，…，Xn)，可做假设如下：

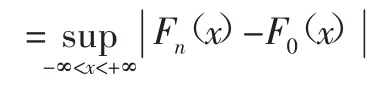
假设检验及结果如表2所示。

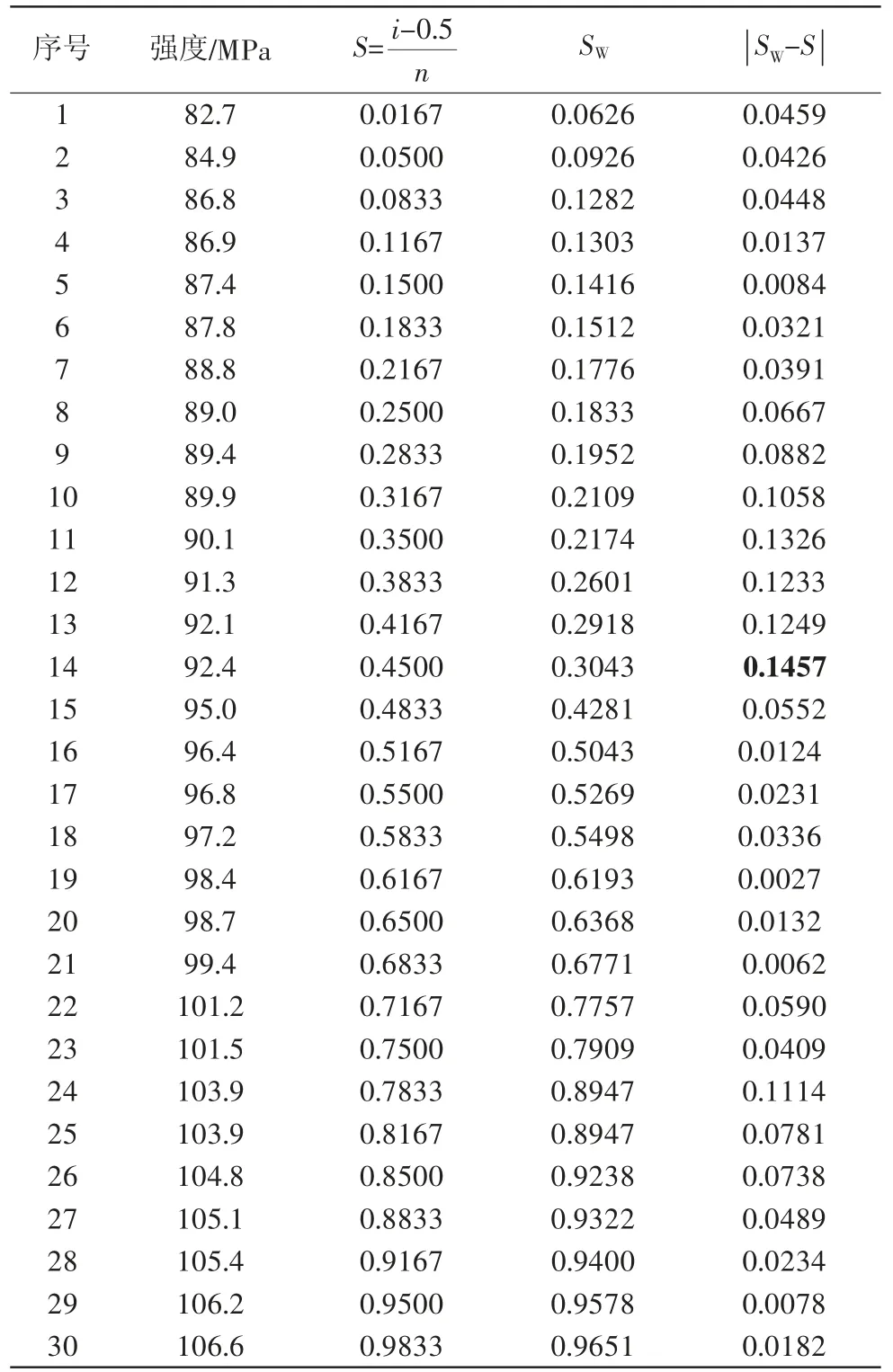
表2 Kolmogorov检验计算和结果

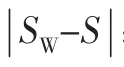
理论累积概率曲线和经验失效概率散点对比图如图3所示，三角点为经验失效概率散点，线条为基于上文的估计参数的双参数Weibull分布理论累积概率曲线，可见散点分散在曲线两侧，散点的分布趋势与曲线走向大致相同，表明双参数Weibull分布较好地模拟了2D-C/SiC复合材料面内剪切强度的分布规律。

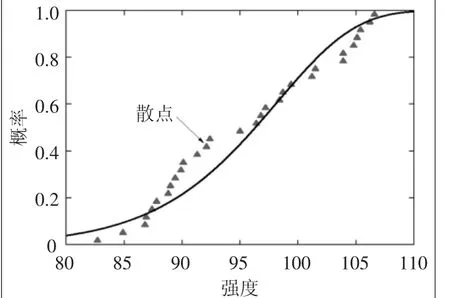
图3 理论累积概率曲线和经验失效概率散点对比图

2.4 强度预测

根据前文的研究表明，2D-C/SiC复合材料面内剪切强度服从双参数Weibull分布，其累计概率分布函数如式（1）所示，可以得到概率密度分布函数如下：

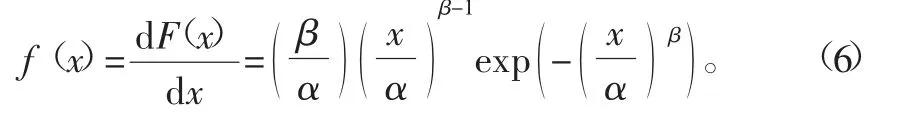
式中：f(x)为双参数Weibull分布概率密度函数；F(x)为双参数Weibull分布累积概率分布函数。

由式（6）可以得到双参数Weibull分布的数学期望和离散系数，分别如式（7）和式（8）所示：

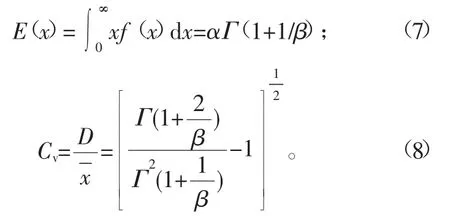
理论计算得到2D-C/SiC复合材料面内剪切强度服从双参数Weibull分布的数学期望和离散系数，如表3所示。由表3可知，数学期望和离散系数的理论预测值与实验值几乎相同，说明利用双参数Weibull分布预测2D-C/SiC复合材料面内剪切强度是合理的。

表3 强度预测结果

3 结论

以双参数Weibull分布为模型，对2D-C/SiC复合材料面内剪切强度性能进行参数估计和假设检验，确定了2DC/SiC复合材料面内剪切强度分布规律，分析对比了分布函数获得的强度预测值与实测值，研究了2D-C/SiC复合材料面内剪切强度分布。结果表明，2D-C/SiC复合材料面内剪切强度服从双参数Weibull分布，利用双参数Weibull分布预测2D-C/SiC复合材料面内剪切强度是合理的。