基于数值计算的偏心率与半径间隙对水润滑轴承性能的影响

雷凯文， 王克俭

（北京化工大学 机电工程学院，北京100029）

0 引言

传统的以润滑油作为润滑介质的舰船尾轴承因密封技术的限制，其在运行过程中每年有大量润滑油泄漏到航行水域当中[1]。经过长时间的积累，势必会造成生态环境的破坏。与传统油润滑轴承相比，水润滑轴承对环境友好。同时，水润滑轴承不需要使用复杂的密封装置，这既能简化轴系构造，亦能节约贵重金属资源[2]。因此，近些年来，对于水润滑轴承的研究越来越多。何涛等[3]研究了不同橡胶轴承厚度对摩擦因数的影响，结果表明，随着橡胶厚度的增大，润滑效果越好，摩擦因数越小。刘洋洋等[4]通过设计不同表面粗糙度，得出随着粗糙度的增加，液膜承载力、偏心率、最大液膜压力和最大粗糙峰接触压力呈减小趋势，粗糙峰接触承载力和最小名义膜厚呈增加趋势的结论。曹玉哲等[5]考虑了橡胶衬层的变形，证明了变形会导致承载力大幅下降与摩擦因数的明显提高。尚明基等[6]通过施加不同载荷，进行了无/有水环境下的摩擦实验，证明了摩擦因数均会先下降后升高，但二者的磨损机理不同。张兴州等[7]采用数值计算方法，得到了随着卷吸速度增大，偏位角增大，偏心率减小，最小膜厚增大；随着载荷参数的增大，偏位角减小，偏心率增大，最小膜厚减小的结论。

综上所述，关于水润滑轴承的研究重点在于优化轴承结构或改善轴承材料本身的性能，以期能提高其承载力的同时降低摩擦因数。本文着眼于轴承结构优化设计，结合目前关于半径间隙与偏心率共同对轴承性能产生影响的研究数据较少，且大多偏心率、半径间隙取值范围较窄的情况，通过Fortran语言，使用数值计算，以半径间隙与偏心率为自变量，得到了较为完善的水润滑轴承性能参数的变化趋势。

1 数学模型

1.1 几何模型

径向滑动轴承通过轴径的旋转运动，将润滑介质带入收敛间隙，从而获得流体动压。在偏位角等于Ψ时，水膜承载力与外载荷平衡，轴承达到平衡状态。由图1可知半径间隙C0=R1-R2，偏心距为e，则偏心率ε=e/C0。

1.2 膜厚方程

根据图1右侧示意图，可计算出水膜厚度h与旋转角度θ的关系式。在△O1O2P中，可以通过正弦定律与几何关系得出水膜厚度h公式：

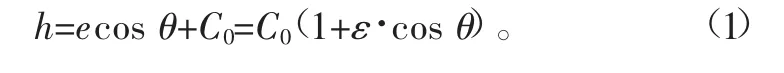
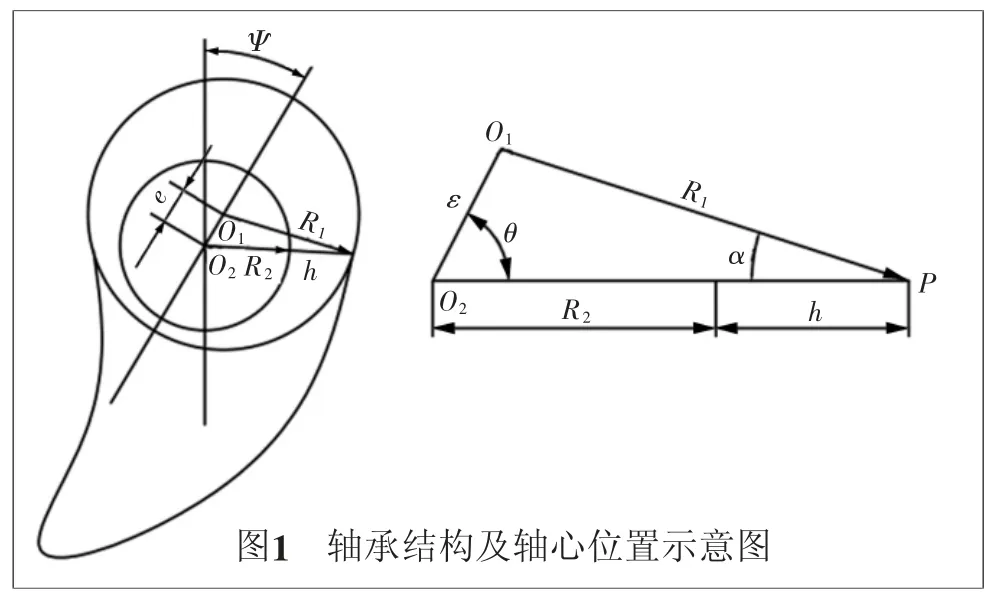
1.3 Reynolds方程

雷诺方程是计算流体润滑过程中各节点压力值的经典方程，在无沟槽轴承建模过程中，除了基本雷诺方程，还需进行一定的计算条件假设。这些假设条件为：1）由于润滑剂采用水介质，黏度低，同时水膜压力较小，故忽略水介质的黏压效应，即忽略由于压力变化而造成的水黏度的变化；2）由于水介质散热性能良好，且轴承工作时完全浸没在水介质中，有良好的散热效果，故忽略水介质的黏温效应，忽略由于摩擦温升而造成的温度变化，即水介质黏度只与环境温度有关；3）认为水介质为不可压缩流体，即忽略密压效应；4）所选轴承材料为橡胶，具有良好的亲水性，故认为在轴承与水介质接触表面无相对速度，即具备边界无滑移条件；5）因为所建立轴承模型无复杂结构，橡胶变形对水膜压力影响较小，故忽略橡胶变形的影响。

对于满足上述假设条件，即忽略黏温效应、黏压效应、密压效应后的Reynolds方程如下：

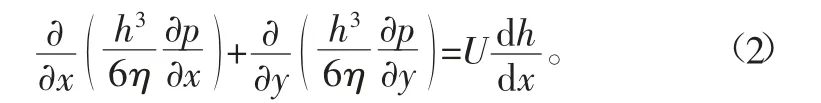
式中：h为水膜厚度；p为水膜节点压强；η为润滑介质黏度；U为转速。

因为是径向滑动轴承，可以将轴承沿轴线展开，使用柱坐标表示上述Reynolds方程，设x=Rθ，dx=Rdθ,则方程如下：

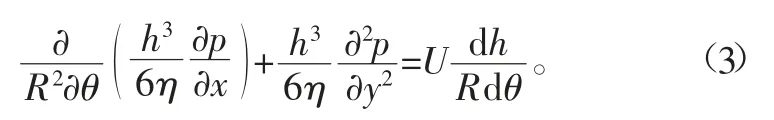
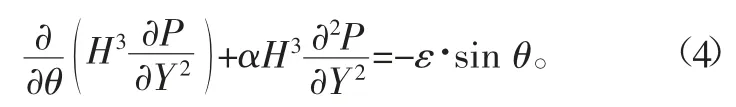
式中：b为轴承宽度；R为轴承半径。

1.4 边界条件

入口处：Y=-1/2，P=0；出口处：Y=1/2，P=0。

2 数值方法

本文采取直接迭代法进行数值计算，即先将轴承延轴线展开，按照膜厚H的计算公式得出各个节点膜厚，随后根据初始压力，通过差分公式与先前计算出的水膜厚度H，计算各个节点压力。通过松弛迭代的方法，对节点压力进行修正，直至其满足迭代误差范围后得出各节点水膜厚度与压力。

因为绝对精度判断准则容易造成压力的不收敛，故采取相对精度判断准则。即满足:

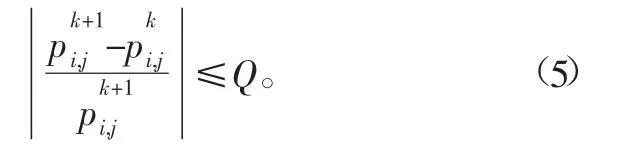
Q为相对精度，对于一般工程问题而言，其取值范围通常是0.01～10-7，本文相对精度取Q=10-7。

同时，在构建轴承数学模型时使用了两个维度，分别是周向方向与轴向方向，分别将周向方向θ与轴向方向平均各取61与21个节点。数值计算程序流程如图2所示。

图2 径向滑动轴承润滑特性计算流程

3 结果与讨论

3.1 基本参数

本节用来计算的轴承结构与工况参数如表1所示。

3.2 半径间隙C0对压力和膜厚的影响

图3～图6给出了在截面Y=0和截面θ=180°水膜压力与水膜厚度随半径间隙C0的变化规律。分析时，取偏心率为0.9。

从图3可知，在Y=0截面上，半径间隙对水膜压力的影响为随着水介质进入收敛区域的角度越大，压力越大，当压力超过峰值时，水膜压力快速下降。同时，半径间隙的不同，并不会影响压力峰值在周向上的位置。

图4表示在Y=0截面上半径间隙C0对水膜厚度的影响，可以看出随着C0的增大水膜厚度也随之增大，但是在收敛区域边界，水膜厚度的差异比起在收敛区域中心的差异来说更为明显。在水膜厚度最小值处，半径间隙的影响效果很小。

由图5、图6可以得到，不论是水膜压力还是水膜厚度，均对Y=0截面对称分布，压力曲线在趋向Y=0截面时，起初数值快速增大，但增大到一个峰值后，有一段平台期，随后快速恢复到0，随着半径间隙C0的增大，压力值的平台期越长。而图6则显示在θ=180°时，水膜厚度刚好处于轴承平衡位置，即压力最大值点，此时，水膜厚度最小，等于轴承间隙C0。

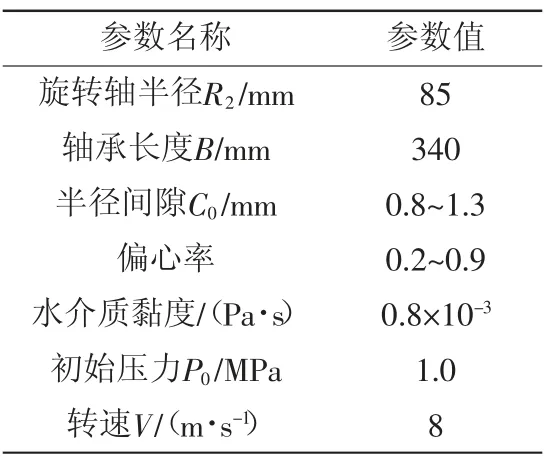
表1 结构与工况参数

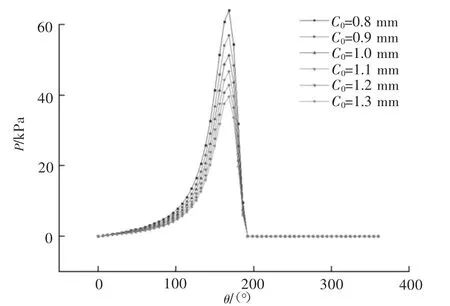
图3 Y=0,半径间隙对水膜压力的影响

图4 Y=0,半径间隙对水膜压力的影响

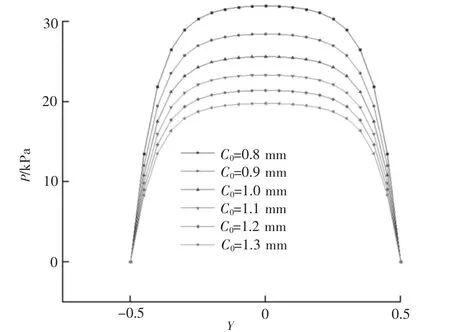
图5 θ=180°,偏心率对水膜压力影响

由图7可知，随着偏心率越大，最大水膜压力越大，同时偏心率越大，压力增大的幅度越大。这是因为偏心率越小，流体动压现象越明显，压力就越大。半径间隙C0增大则会降低流体动压效果，所以随着C0越大，最大压力越小。

由图8可知，随着偏心率的增大，最小膜厚值减小，同时，在同一偏心率下，半径间隙C0越大，最小膜厚值越大，这是因为轴承完全浸没于水介质中，随着C0越大，在最小膜厚处，水膜厚度越大。

图7 偏心率、半径间隙对最大压力的影响

图8 偏心率、半径间隙对最小膜厚的影响

3.3 半径间隙对承载力与摩擦因数的影响

图9展示了承载力在不同结构参数下的变化趋势。在同一轴承间隙C0下，随着偏心率的增大，承载力增大，这是因为偏心率越大，在轴承承载区的压力越大，即流体动压现象越明显，故而承载力越大，同时，偏心率越大，承载力上升得越明显。然而，在轴承间隙C0变大的情况下，流体动压效果降低，承载力下降，但是这有益于降温，所选轴承材料为橡胶，温度对其有一定的影响，故偏心率也不宜过大。

由图10可以看出，随着偏心率的增大，摩擦因数起初快速下降，但随后逐渐变得平缓。

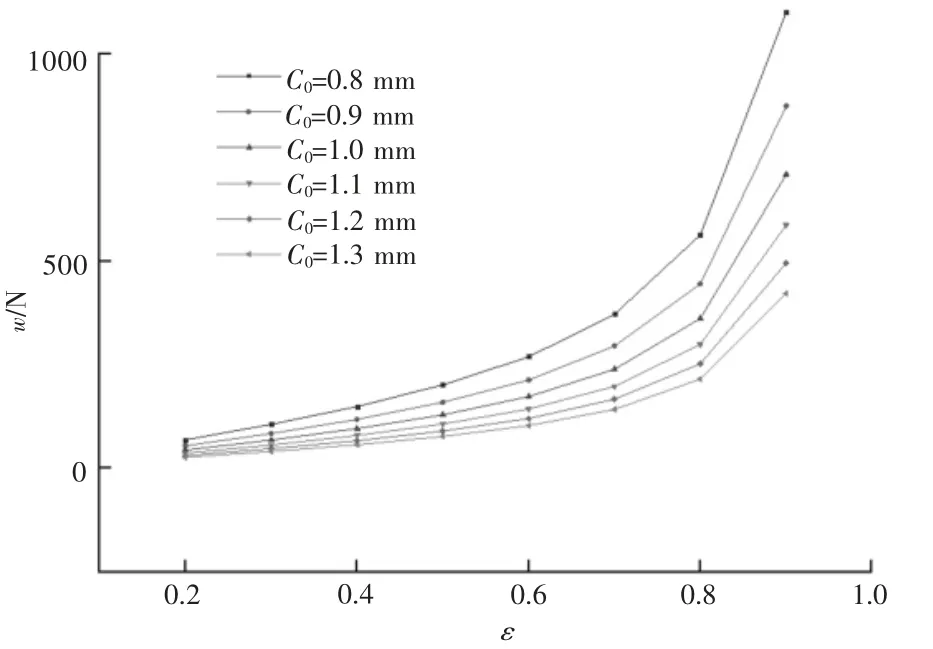
图9 偏心率、半径间隙对摩擦因数的影响

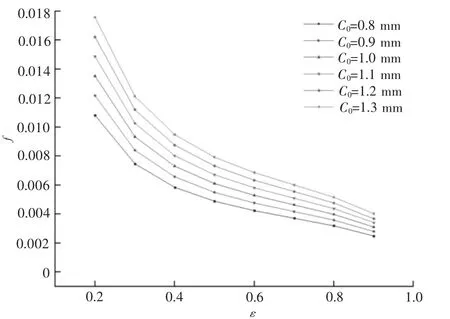
图10 偏心率、半径间隙对承载力的影响

与承载力的不同之处在于，轴承间隙C0的增大反而会导致摩擦因数的增大，造成这种现象的解释就是，随着轴承间隙C0的增大，摩擦力F也随之增大，同时其增大的速率要高于承载力W的增大速率，才会导致这种曲线的生成。

4 结论

1）建立了考虑半径间隙与偏心率对水润滑径向轴承各性能参数影响的数值模型。

2）数值计算了偏心率为0.2～0.9，半径间隙为0.8～1.3 mm之间等结构参数对水膜压力、水膜厚度、承载力及摩擦因数的影响，结果表明，随着半径间隙的减小，水膜压力呈现升高的趋势，水膜厚度则会降低。

3）半径间隙的降低与偏心率的升高会导致摩擦因数的降低。