局部时间步法在低马赫燃烧模拟中的适用性研究

姚 卫，孙 超，刘 杭，吴 梅，杨少波，曹顺利

局部时间步法在低马赫燃烧模拟中的适用性研究

姚 卫1, 2，孙 超3，刘 杭1，吴 梅4，杨少波3，曹顺利3

(1. 中国科学院力学研究所高温气体动力学国家重点实验室，北京 100190；2. 中国科学院大学工程科学学院，北京 100049；3.中国船舶工业系统工程研究院，北京 100094；4.合肥工业大学土木与水利工程学院，合肥 230009)

在复杂燃烧模拟中由于整场流速的不均匀性和局部网格尺寸的差异，各局部流场区域的CFL数差异较大．传统的基于整场最大CFL数定义的整体时间步法严重制约计算效率．本文首次考察了基于当地CFL数限制的局部时间步法在低马赫数湍流燃烧模拟中的适用性．对开放空间中甲烷池火(1065万网格)和封闭空间建筑火灾(320万网格)的大涡模拟表明，采用局部时间步法相比于整体时间步法分别实现了6倍和8倍的加速比．加速比随网格尺度减小呈增加趋势．研究进一步从两个方面验证了局部时间步法在低马赫数燃烧模拟中的准确性：①与实验数据的对比表明，由于低马赫数燃烧的准稳态特性，局部和整体时间步法均较为准确地预测了温度的时间变化特性；②对时均流场的比较表明，除微量痕迹物(质量分数小于0.1%)以外，两种方法对时均温度、时均速度和氧气体积分数的预测差异均较小．研究中还对现有的PaSR湍流燃烧模型和压力求解算法进行了改进和优化，以分别提高其物理准确性和鲁棒性．

湍流燃烧；局部时间步法；大涡模拟；CFL数；OpenFOAM

低马赫数燃烧是日常生活中最常见的一种燃烧形式，例如各类火灾和非动力装置类锅炉内部燃烧．在各类跨声速甚至高超声速航空航天发动机燃烧室中也存在较大区域的局部低马赫数燃烧．低马赫数燃烧的特点是：①压力波动较小近似恒定，因此可按照不可压缩流体处理；②燃烧化学反应特征时间相对流动特征时间较小，因此快速反应假设成立且流动化学反应可以近似解耦计算；③流速远小于声速，压力波近似以无限快速度传播，无黏流动部分呈现椭圆型流动特征．针对上述流动特点，低马赫燃烧求解可以采取基于压力驱动速度原理的压力求解器，并且基于气体状态方程耦合燃烧化学反应效应实现流动和燃烧的隐式求解以降低对时间步的CFL(Courant-Friedrichs-Lewy)约束(CFL数＝速度×时间步/网格尺度，一般要求此数小于某一定值以保证数值格式的稳定性)．在复杂燃烧流场中由于整场流速的不均匀性和局部网格尺寸的差异，各局部流场区域的CFL数差异较大．特别是在模拟复杂几何结构或需要捕捉局部精细流场结构(如近壁边界层或火焰反应区)时通常需要使用非均匀或局部自适应网格，根据CFL约束时间步正比于网格尺度．传统方法中整场使用单一时间步，通常使得时间步受限于整场最小网格尺度，因而显著降低了计算效率．而如果能够针对局部流场采用多重时间步，将可在满足CFL约束的前提下显著提高计算效率．

基于局部时间步(local time-stepping)的局部时间步法由Osher与Sanders[1]在求解一维标量守恒律方程时提出，其主要原理为在满足局部稳定性条件下，每个网格单元拥有独立的局部时间步长并可在计算过程中自适应更新．相比于所有网格单元按统一时间层更新的方法，一方面提高了计算效率，另一方面也加速了流场收敛．空间差异的多重时间法等效于对控制方程的空间预处理，可以一定程度上消除空间梯度较大区域的刚性[2]．多重时间法成功应用于基于笛卡尔网格的自适应网格加密(AMR)算例[3-4]，其通过解耦非加密区域与局部加密区域的时间步有效提高了计算效率并且实现了对加密区域流场结构(如激波)的准确捕捉．Dumbser等[5]和Taube等[6]在涉及网格尺度剧烈变化的对弹性波和Maxwell方程的任意高阶间断有限元(DG-FEM)模拟中耦合了显式局部时间步法以提高计算效率和收敛速率．Qi等[7]通过耦合间断有限元和单步高阶泰勒式时间积分格式实现了对局部时间步法在基于多尺度网格的瞬态电磁波模拟中的支持．Grote等[8]推导了局部时间步法与任意高阶显式Runge-Kutta方法的耦合形式并成功应用于多尺度网格波方程求解. Lilia[9]在基于局部时间步的二阶Runge-Kutta格式中构造了更加准确的二次多项式以计算时间步相异的相邻网格界面值．Ashbourne[10]进一步将Lilia[9]的方法拓展到三阶和四阶Runge-Kutta格式并改进了网格界面插值的多项式逼近方法．杜永乐等[11]和姜婷婷等[12]在稀薄气体的DSMC模拟中采用了类似的局部自适应时间步方法表明其可以在保真的前提下显著提高流场收敛速率．谭志军等[13]基于局部时间步法和自适应网格加密方法对一维对流扩散方程所做的测试表明实现了2～3倍的加速，同时未见明显的精度降低．吴迪等[14]基于局部时间步法在超声速后台阶流的三维欧拉方程模拟中相比于整体时间步长法最高取得了5倍的加速比．胡鹏等[15]基于局部时间步长的水沙耦合模拟表明，该方法能够在保证精度的前提下节省高达92%的计算时间．Espinoza等[16]在基于局部时间步法的可压缩高速和超声速稳态流动模拟中分别观测到了2.56和8.96倍的迭代收敛速度．最近，除了基于当地CFL数控制局部时间步以外，Kalkote等[17]提出了一种基于当地截断误差控制的局部自适应时间步方法．Jeanmasson等[18]则对局部时间步法进一步发展了通量守恒修正．

目前基于局部时间步的局部时间步法在湍流燃烧中的应用还不多见．而湍流燃烧通常需要对主要释热的反应区域重点求解，意味着需要采用较密的局部网格，而对其余的无反应区域可以采用相对较粗的网格．特别是在火灾模拟中，由于模拟场景相对火源区域一般较大，为了提高计算效率一般仅对火源区域局部加密．另外在涉及复杂几何结构的燃烧室或建筑火灾模拟中，对于曲率较大的结合拐角需要局部加密以逼近几何外形．燃烧和火灾一般发生于受限空间内，如发动机和室内，为了准确模拟近壁效应一般需要对壁面边界层区域采用附加膨胀层的方法局部加密．因此针对湍流燃烧模拟，如果采用整体时间层统一的时间步，将使得时间推进受限于火源、拐角和近壁等区域处的最小时间步．而通常局部加密区域仅占整体计算域较小的体积分数．按照通常火灾模拟中火源、拐角和近壁等区域局部加密设置，最大最小网格尺度一般相差3～5倍来估算，采用局部时间步法预计至少将可使计算效率提高3～5倍．在并行环境下，位于火源局部加密区域的分区节点因需求解化学反应计算载荷通常较大，而其他对应无反应区的节点计算负担较小，从而导致计算载荷的严重不均衡．而采用局部时间步法，对应无反应区的计算节点可将额外的计算资源用于时间上的加速推进(大时间步一般意味着更多的迭代次数和收敛时间)，因而也可以在一定程度上缓解计算载荷的不均衡性．

火灾和内燃等面向实际应用的低马赫数燃烧模拟的两大主要特点为：(1)模拟工况尺寸较大且内部几何结构复杂，计算区域尺寸可跨越数十米甚至上百米；(2)完整的燃烧起始、发展和熄火过程模拟需要求解较长的时间历程，对应物理时间可达数分钟(约600s)甚至1h．例如大型建筑火灾[19-20]、隧道火  灾[21-22]、舰船火灾[23]、工业燃烧锅炉[24-26]模拟等．这些低马赫数燃烧场景模拟一方面对计算效率有特殊的实际需求，另一方面又存在需要着重求解的区域(如火源、疏散口、重点热防护部件等)．模拟中需要兼顾计算效率与求解精细度，而对最终结果一般仅关注重点区域的稳态流场．传统的燃烧模拟程序侧重于对小尺寸(如射流火焰)或局部燃烧场的高精度、高保真模拟，所采用的时空高阶格式一方面显著增加了计算代价，另一方面也削弱了求解复杂流场的鲁棒性，在工程燃烧模拟中的适用性较弱．

本研究针对火灾等低马赫数燃烧模拟需求开发了基于局部时间步法的压力校正隐式燃烧求解器，并将其应用于开放空间池火和封闭空间建筑火灾模拟中以进一步验证其准确性和计算效率．本文将首先介绍局部时间步法的实现算法、对PaSR湍流燃烧模型的改进以及对压力求解算法的稳定性优化等技术细节，进而结合具体算例分析局部时间步法与整体时间步法对湍流燃烧时均流场的量化影响，以考察局部时间步法在低马赫数湍流燃烧中的适用性．

1 数学和物理模型

1.1 控制方程

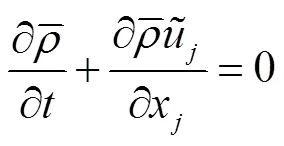
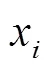
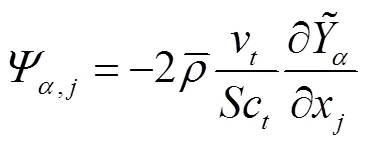
1.2 改进型PaSR湍流燃烧模型

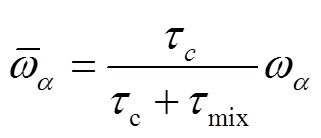
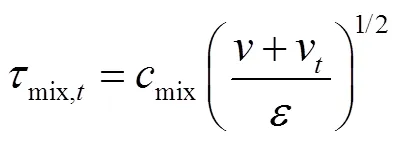
1.3 基于鲁棒增强型PIMPLE算法的隐式压力求解

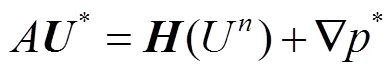
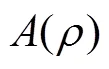
1.4 基于局部时间步的高效多重时间法

1.5 基于OpenFOAM的求解器与算例设置

本求解器开发的主要目的是为火灾等低马赫数准稳态燃烧模拟提供高效、准确且鲁棒性较好的计算平台．为提高算例的普适性，拟分别针对开放和封闭空间两种典型燃烧情形进行计算验证．为提高算例的标准性，算例选取为FireFOAM自带的标准开放空间池火和封闭空间单室建筑火灾算例．其中开放池火为理想算例，研究主要比较两种方法预测的差异；而单室建筑火灾为实验测试算例，研究结合实验数据对两种方法预测的准确性进行了验证．在以下计算中，整体时间步算例采用原FireFOAM求解器(不支持多重时间步功能)计算，多重时间步则采用改进的求解器(命名为Amber)进行．本研究主要目的为验证局部时间步法与传统的整体时间步法在预测关键燃烧场特性(如温度、速度、组分浓度等)的准确性与计算效率．物理模型和数值方法对燃烧物理过程的影响分析不是本研究的重点，拟在后续研究中开展．

2 结果与讨论

2.1 开放空间内池火模拟

该算例模拟了一个典型的开放空间内池火工况．计算域为1m×1m×1m的立方形空间，在底部中央有一0.2m×0.2m的方形火源区域．燃料为气态甲烷，常温(300K)常压(101325Pa)下以法向速度0.01m/s喷入并发生燃烧．模拟中考虑重力效应，火焰受浮力诱导的自然对流驱动．由于计算区域的规则性，网格多为正六面体正交网格，整体区域网格尺度为0.5mm，由于整场网格尺度已经满足大涡模拟要求(由网格尺度决定的截断波数位于惯性子区)，火源区域不再局部加密，整体网格数目为800万．该算例总模拟时间为100s，以特征速度1m/s计算约为100个整场流通时间(FTT)，其单FTT时间为0＝1s．图1(a)比较了不同网格条件下的中心轴线速度分布，可见随着网格密度增加，预测结果趋于相同，并且最终与整体时间步法的预测接近．这里定义误差为与最密网格(1065万)预测的相对误差．由图1(b)可见，平均误差与最大误差均随网格尺度减小而减小，平均误差随网格尺度近似呈指数衰减(对数空间表现为线性)．在网格密度大于800万的情况下，平均误差小于0.5%，最大误差小于2%，满足网格独立性要求．以下分析如不特殊指明，均基于1065万网格结果．

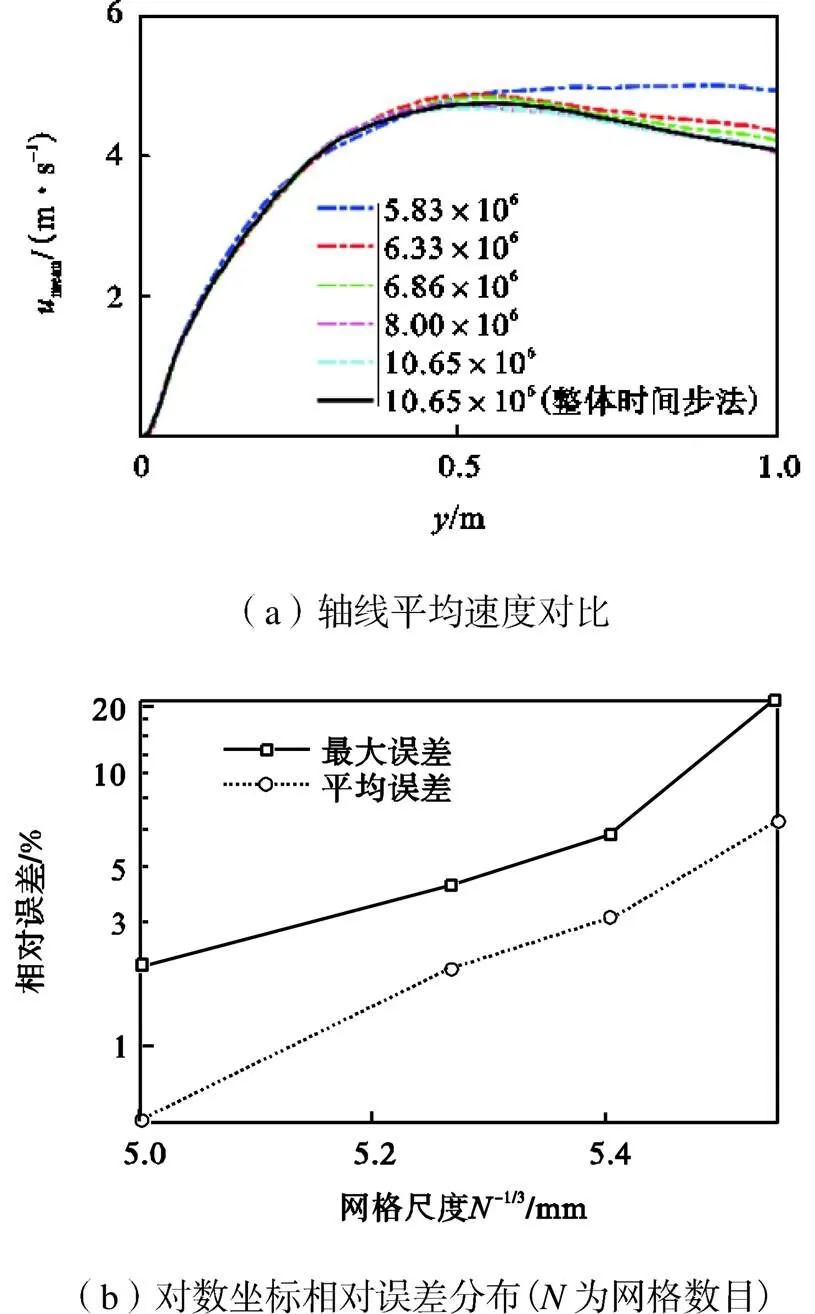
图1 局部时间步法的网格收敛性分析

图2 火焰中心剖面局步时间步分布

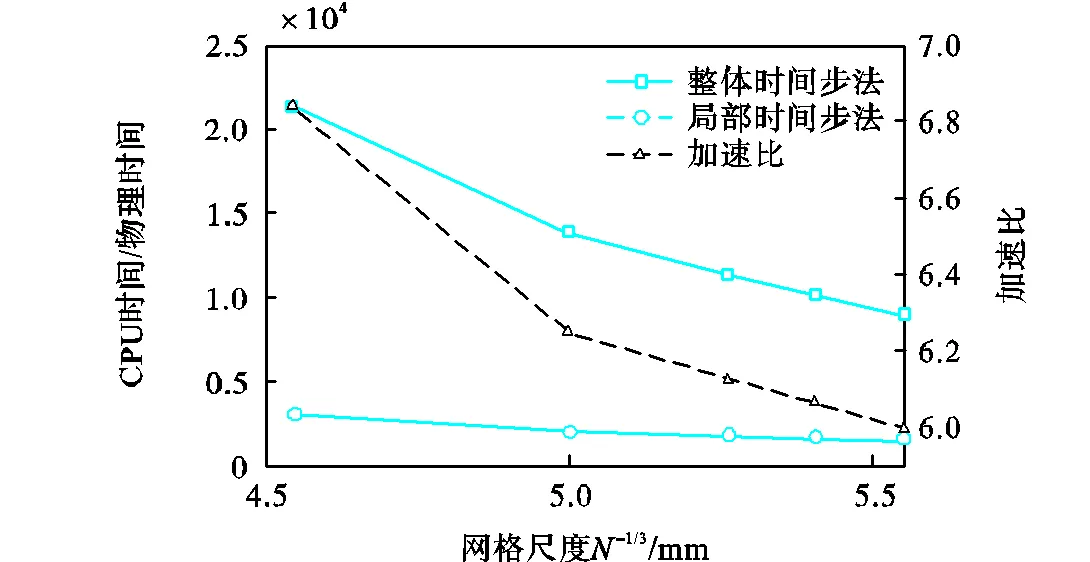
图3 无量纲计算周期和加速比对网格尺寸的依赖性关系

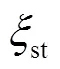
图5定量比较了中心轴线的时均值．火焰高度(＝0.6m)以下的时均值分布几乎相同，之后差异越往下游越大，但整体差异仍较小．采用局部时间步法，温度和速度峰值与采用整体时间步法预测基本一致，但平均氧气消耗率略低，火焰温度和最终浮力驱动速度也略低于整体时间步法的预测．在中心轴线上各关键变量的平均差异分别为1.3%(温度)，0.7%(速度)，3.9%(CH4)，3.7%(O2)，均小于5%，可以近似认为采用局部时间法和整体时间法对时均结果的预测一致．

多重时间步法等效于对时间项的权重预处理，有限体积方法中，相邻网格单元交界面的质量通量计算与时间无关，根据单元内质量、动量、组分和能量等的守恒原则时间权重影响各网格单元值更新的快慢．时间步较大的区域快速演化迅速趋于准稳态，而时间步较小的区域各变量相当于处于相对“冻结”状态．不同区域交界处互为边界条件，意味着时间演化较快的区域通过提供一个快速趋于准稳态的边界加速了其相邻时间演化较慢区域的收敛．本算例中，以射流边界为区分，可将火焰流场分为演化较慢的火焰中心区域和快速趋于稳态的伴流．伴流通过为中心射流提供了更趋于稳态的射流边界条件，加速了中心火焰区的收敛，类似于Espinoza等[16]在可压缩高速流动中的观察．因而采用局部时间步法从两个方面促进了准稳态流场的建立：一方面通过增加时间步加速了无反应区域的演化，另一方面通过边界效应促进了相对演化较慢的火焰区域往准稳态收敛的进度.

图5 中心轴线上时均值比较

2.2 封闭空间内池火模拟

计算区域为典型的两室建筑，其中左边房间尺寸为0.4m(长)×0.4m(宽)×0.6m(高)，右边紧邻房间的尺寸为0.4m(长)×0.4m(宽)×0.4m(高)．直径0.095m的圆形火源位于右侧房间底部中央．在两个相邻房间由一堵厚度为25.4cm的墙隔开，墙的底部和顶部各留有30cm的间隙分别用于通风和排烟．整体网格数目为320万，其中围绕火源区域的0.2m(长)×0.2m(宽)×0.3m(高)的区域局部加密网格．左侧房间顶部和侧边为开放边界条件，固定压力为环境大气压(101325Pa)．右侧房间为完全封闭空间，仅通过通风口和排烟孔和外界平衡压力．

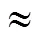
在火焰的发展演化过程中，新鲜空气从左侧吹入带来的动量使火焰偏向右方．同时由于左侧顶部的抽吸，热烟气层向左上方移动．相比较而言，右侧房间中靠近右壁面一侧的气流速度较大，相应地，图6中的局部时间步右侧较小．左侧房间通过快速时间演化相当于为右侧房间的流场发展提供了一个稳定的边界条件，而右侧房间内的计算域时间步较小，数值耗散更低，有利于捕捉到更加丰富的火焰瞬态效应.这也意味着，通过采用多重时间步，对着重关注的瞬态流动区域指定较小的时间步，在对物理过程精细捕捉的同时兼顾计算效率．

图6 时间步分布

图7比较了采用局部时间步法和整体时间步法的瞬态温度和O2体积分数预测结果．总体上两种方法的预测与实验测量值的趋势均吻合较好．局部时间步法可以比整体时间步法更快地收敛到稳态解[16]，因此局部时间步法更适用于稳态流场模拟．对于低马赫数燃烧问题流动速度远小于声速，压力波以近乎无限快的速度在整场传播，驱动速度场更快地达到平衡，并且流动特征时间远大于化学反应特征时间，流动和燃烧均趋于准稳态，因此局部时间步法较为适用．局部时间步方法更适用于最终达到稳态或准稳态的流场模拟，通过快速演化区域与慢演化区域的互为边界原理实现了整体的加速收敛．由于时间步较大区域的单步时间内变量增幅较大，相应地会表现出较大的脉动值，如图中所示．在火源上方0.14m和0.26m高度位置整体时间步法的预测更贴近实验值，0.38m处前半段整体时间步法预测较好而后半段局部时间步预测更贴近测量值．在初始点火(0～40s)和熄火阶段(310～350s)，由于释热速率的急剧变化导致瞬态效应较强，两种方法的预测均存在一定偏差．靠近火源根部(＝0.14m高度处)燃料和空气掺混后反应剧烈，表现在测量和预测上温度空间波动均较大，而高处羽流区反应微弱因而温度波动更为平稳．图7(d)中两种方法对氧气浓度的预测在中间准稳态阶段均与实验测量值吻合较好，其中由于时间步的增加，局部时间步法的预测表现出较大的脉动.

图8比较了稳定燃烧阶段(取＝200s处燃烧速率)基于局部时间步法和整体时间步法预测的时均值分布．为方便对比，在图例范围内标识了5条等间距轮廓线．整体而言，两种方法预测的时均流场相似度较高．对于时均温度，采用局部时间法预测的火焰高温核心区域略宽而高度相似．时均速度未见明显差异．从温度和速度分布可以明显看出，由于左下部空气的通入，使得火焰向右侧倾斜明显．又由于左上部的抽吸作用，热羽流向左侧移动．整体火羽流路径呈现反C字型．从产物H2O和CO2的分布看，热燃烧产物在浮力作用下上升到顶棚以后，左侧的部分被排烟通道抽吸走，右侧的部分被右侧仓壁阻挡后沿着壁面向下堆积．与温度的分布类似，采用局部时间步法预测的核心羽流区(高温高产物浓度轮廓线标识)的宽度稍窄．在火灾发展过程中，左房间为半开放空间(上、左、前、后均为自由开放边界条件)，因而左侧房间的流场趋于稳态，两种方法的预测更为相似．

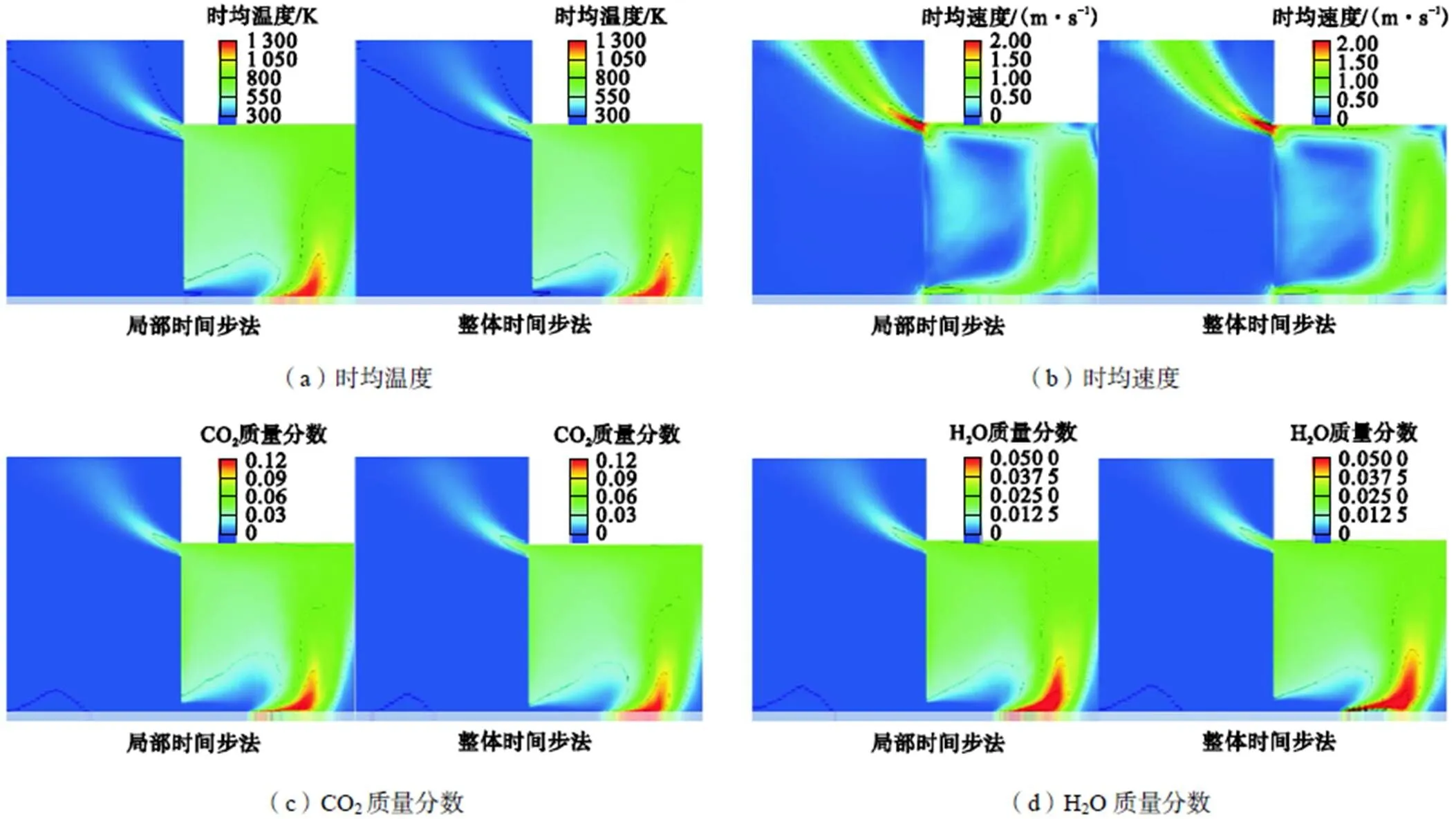
图8 火源中心剖面时均温度、速度、CO2和H2O质量分数分布

图9量化比较了图8中从火源到顶棚(＝0.1～0.39m)不同高度处横向的时均量分布．对于燃料C7H16，在＝0.1m靠近火源底部浓度较大两种方法预测的偏差较小．随着高度增加，燃料浓度逐渐降低至千分之一量级，微量痕迹物的预测相对误差增加．对于氧气质量分数，两种方法的预测在不同高度处量级和趋势均较为相似．对于温度分布二者的预测几乎没有差别，尤其是对于火源区域的温度峰值和近壁区域的温度陡降均吻合较好．在反C型流场的中部，由于底部进气道向右气流动量和火羽流向上浮力的驱动会形成一回流区．速度分布显示该回流区底部(0.1m)进气口位置在采用局部时间法时略低于整体时间步法．0.3m高度处局部时间步法预测的速度峰值略低，这也对应图8中较窄的高温区域(浮力较弱)．各时均量在4个高度处的平均相对误差分别为1.1%(温度，0.1～0.39m)、6.1%(速度，0.1～0.39m)、1.0%(氧气质量分数，0.1～0.39m)、5.0% (C7H16浓度，0.1～0.2m高度)，＞100%(C7H16浓度，0.3～0.39m高度)，可见除了燃料因浓度衰减较快导致远离火焰区相对误差较大以外，其他量的预测误差均较小．采用局部时间步法，增加了弱流动区域的时间步，因而一定程度上增加了数值耗散性，这有可能是引起上述差异的原因，然而整体上二者的时均结果十分相近，表明了局部时间步法在低马赫数准稳态燃烧问题中的适用性，以及牺牲非主要燃烧反应区微量痕迹物的预测精度以显著提高整体计算效率是可行的．

3 结 语

本研究基于局部时间步法、改进PaSR湍流燃烧模型以及优化压力求解算法开发了面向低马赫数的压力求解器，并选取了开放空间和封闭空间两种典型的低马赫数燃烧算例进行了验证．一般可认为，局部时间步法的加速比近似与网格差异化程度成正比．按照通常的火源、拐角、近壁等区域局部加密设置，最大/最小网格尺度一般至少相差3～5倍，采用局部时间步法预计至少可使计算效率提高3～5倍．本文中的网格设置使得局部时间步法相比于整体时间步法分别实现了6倍和8倍的实际加速比．实际加速比通常略小于由平均时间步之比定义的理想值，这是因为除了时间步计算本身的额外代价外，辐射和刚性化学反应求解一般耗时较多且与流动时间步关系较小．总体上计算周期随网格尺寸减小近似呈线性增加，其中整体时间步法计算周期的上升梯度更大，表明密网格条件下局部时间步法有更好的加速效果．与实验数据的对比表明，局部和整体时间步法均较为准确地预测了温度的时间变化特性和除微量痕迹物以外的时均流场特性，表明了局部时间步法在低马赫数准稳态燃烧问题中的适用性，以及牺牲非主要燃烧反应区微量痕迹物的预测精度以显著提高整体计算效率是可行的．

一般而言，局部时间步法针对稳态流动或统计上呈现稳态的准稳态流动问题，其得到的结果是比较可靠的，但对于强瞬态的流场演化问题，其方法的适用性则需要进一步的研究探讨．

［1］ Osher S，Sanders R. Numerical approximations to nonlinear conservation laws with locally varying time and space grids[J].，1983，41(164)：321-336.

［2］ Powell K G，van Leer B. A genuinely multi-dimensional upwind cell-vertex scheme for the Euler equations[C]//. Reno，USA，1989.

［3］ Berger M J，Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations[J].，1984，53(3)：484-512.

［4］ Berger M J，Colella P. Local adaptive mesh refinement for shock hydrodynamics[J].，1989，82(1)：64-84.

［5］ Dumbser M，Käser M，Toro E F. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—V. Local time stepping and-adaptivity[J].，2007，171(2)：695-717.

［6］ Taube A，Dumbser M，Munz C D，et al. A high-order discontinuous Galerkin method with time-accurate local time stepping for the Maxwell equations[J].：，，2009，22(1)：77-103.

［7］ Qi H，Wang X，Zhang J，et al. An ADER discontinuous Galerkin method with local time-stepping for transient electromagnetics[J].，2018，229：106-115.

［8］ Grote M J，Mehlin M，Mitkova T. Runge-Kutta-based explicit local time-stepping methods for wave propagation[J].，2015，37(2)：A747-A775.

［9］ Lilia Krivodonova. An efficient local time-stepping scheme for solution of nonlinear conservation laws[J].，2010，229(22)：8537-8551.

［10］ Ashbourne A. Efficient Runge-Kutta Based Local Time-Stepping Methods[D]. Waterloo，Canada：University of Waterloo，2016.

［11］ 杜永乐，阎 超. DSMC方法中的自适应当地时间步长法[J]. 北京航空航天大学学报，2006，32(4)：388-390.

Du Yongle，Yan Chao. Adaptive local time step method for DSMC code [J].，2006，32(4)：388-390(in Chinese).

［12］ 姜婷婷，钱 坤，陈伟芳. 高超声速混合流动的粒子模拟耦合算法[J]. 固体火箭技术，2017，40(3)：283-288.

Jiang Tingting，Qian Kun，Chen Weifang. Study on hybrid particle simulation method for hypersonic mixed flows[J].，2017，40(3)：283-288(in Chinese).

［13］ 谭志军，黄云清. 对一维守恒律的一种局部时间步长自适应网格方法[J]. 湘潭大学自然科学学报，2003，25(2)：110-116.

Tan Zhijun，Huang Yunqing. An adaptive grid method with local time stepping for one-dimensional conservation laws[J].，2003，25(2)：110-116(in Chinese).

［14］ 吴 迪，蔚喜军，徐 云. 局部时间步长间断有限元方法求解三维欧拉方程[J]. 计算物理，2011，28(1)：1-9.

Wu Di，Wei Xijun，Xu Yun. A discontinuous Galerkin method with local time stepping for Euler equations[J].，2011，28(1)：1-9(in Chinese).

［15］ 胡 鹏，韩健健，雷云龙. 基于局部分级时间步长方法的水沙耦合数学模拟[J]. 浙江大学学报(工学版)，2019，53(4)：743-752.

Hu Peng，Han Jianjian，Lei Yunlong. Coupled modeling of sediment-laden flows based on local-time-step approach[J].()，2019，53(4)：743-752(in Chinese).

［16］ Espinoza D E R，Scanlon T J，Brown R E. Validation of tools to accelerate high-speed CFD simulations using OpenFOAM[C]// 20. Glasgow，UK，2015.

［17］ Kalkote N，Assam A，Eswaran V. Towards developing an adaptive time stepping for compressible unsteady flows[J].，2019，29(2)：487-503.

［18］ Jeanmasson G，Mary I，Mieussens L. On some explicit local time stepping finite volume schemes for CFD[J].，2019，397：108818.

［19］ Cant R S. Modelling and simulation of accidental combustion in complex geometries[C]//. Edinburgh，UK，2007.

［20］ 姜 蓬，邱 榕，蒋 勇. 基于数值模拟的某大厦特大火灾过程调查[J]. 燃烧科学与技术，2007，13(1)：76-80.

Jiang Peng，Qiu Rong，Jiang Yong. Investigation of a mansion fire based on numerical simulation[J].，2007，13(1)：76-80(in Chinese).

［21］ Wang H Y. Prediction of soot and carbon monoxide production in a ventilated tunnel fire by using a computer simulation[J].，2009，44(3)：394-406.

［22］ Ji J，Guo F，Gao Z，et al. Numerical investigation on the effect of ambient pressure on smoke movement and temperature distribution in tunnel fires[J].，2017，118：663-669.

［23］ Su S，Wang L. Three dimensional reconstruction of the fire in a ship engine room with multilayer structures[J].，2013，70：201-207.

［24］ 王秋红，王 超，张小桃，等. 四角切圆锅炉炉内燃烧数值模拟[J]. 热力发电，2016，45(9)：61-66.

Wang Qiuhong，Wang Chao，Zhang Xiaotao，et al. Numerical simulation of combustion process in a tangentially pulverized-coal-fired boiler under variable load operation[J].，2016，45(9)：61-66(in Chinese).

［25］ 张 成，朱天宇，殷立宝，等. 100MW燃煤锅炉污泥掺烧试验与数值模拟[J]. 燃烧科学与技术，2015，21(2)：114-123.

Zhang Cheng，Zhu Tianyu，Yin Libao，et al. Field test and numerical simulation for co-combustion of sludge in a 100 MW coal fired boiler[J].，2015，21(2)：114-123(in Chinese).

［26］ 马 仑，方庆艳，张 成，等. 600MW W型火焰锅炉拱上二次风低NO燃烧特性的数值模拟及优化[J]. 燃烧科学与技术，2016，22(1)：64-70.

Ma Lun，Fang Qingyan，Zhang Cheng，et al. Numerical simulation and optimization for the influence of the arch secondary airon low-NOcombustion characteristics of a 600MW down-fired boiler[J].，2016，22(1)：64-70(in Chinese).

［27］ Yoshizawa A. Statistical theory for compressible turbulent shear flows，with the application to subgrid modeling[J].，1986，29(7)：2152-2164.

［28］ Golovitchev V I，Nordin N，Jarnicki R，et al. 3-D diesel spray simulations using a new detailed chemistry turbulent combustion model[C]//. Paris，France，2000，2000-01-1891.

［29］ Kjaldman L，Brink A，Hupa M. Micro mixing time in the eddy dissipation concept[J].，2000，154(1)：207-227.

［30］ Chomiak J，Karlsson A. Physical and chemical effects in diesel spray ignition[C]//21. Interlaken，Swizerland，1995.

［31］ Fureby C. LES for supersonic combustion[C]//. Tours，France，2012，2012-5979.

［32］ Chomiak J，Karlsson A. Flame liftoff in diesel sprays[J].()，1996，26(2)：2557-2564.

［33］ Hallaji M，Mazaheri K. Numerical simulation of turbulent non-premixed combustion in diluted hot coflow using PaSr combustion model[C]//. Sardinia，Italy，2011.

［34］ Yao W，Lu Y，Wu K，et al. Modeling analysis of an actively cooled scramjet combustor under different kerosene/air ratios[J].，2018，34(4)：975-991.

［35］ John D A J. Inviscid high-temperature nonequilibrium flows.[M]. 2nd Edition. Virginia，USA：AIAA，2006.

［36］ Weller H G，Tabor G，Jasak H，et al. A tensorial approach to computational continuum mechanics using object oriented techniques[J].，1997，12(6)：620-631.

［37］ Murthy J Y，Mathur S R. Finite volume method for radiative heat transfer using unstructured meshes[J].，1998，12(3)：313-321.

Study on Applicability of Local Time-Stepping Method in Low-Mach Combustion Simulation

Yao Wei1, 2，Sun Chao3，Liu Hang1，Wu Mei4，Yang Shaobo3，Cao Shunli3

(1. Key Laboratory of High-Temperature Gas Dynamics，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China；2. School of Engineering Science，University of Chinese Academy of Sciences，Beijing 100049，China；3. China Shipbuilding Industry Systems Engineering Research Institute，Beijing 100094，China；4. College of Civil Engineering，Hefei University of Technology，Hefei 230009，China)

Due to the non-uniformity of flow speed in the whole field and the difference in local grid size in complicated combustion simulations，the local Courant-Friedrichs-Lewy(CFL)number varies significantly among different local flow field regions. The computational efficiency is also severely restricted by the conventional global time-stepping method，which is on the basis of the definition of maximum CFL number. In this paper，the applicability of the local time-stepping method restricted by the local CFL number to low-Mach turbulent combustion simulation is investigated for the first time. Through the large-eddy simulation of an open methane pool fire(with 10.65 million cells)and an enclosed building fire(with 3.2 million cells)，it is shown that the local time-stepping method can achieve speedup ratios of 6 and 8 compared with the global time-stepping method，respectively. The speedup ratio rises with the reduction of grid size. Moreover，the accuracy of the local time-stepping method applied in the low-Mach combustion simulation is validated from two aspects. First，in comparison with the experimental data，the time-varying characteristics of temperature are accurately predicted by both the local and global methods，which is probably due to the quasi-steadiness of low-Mach combustion. Second，in comparison with the time-averaged flow field，the differences in time-averaged temperature，time-averaged velocity，and the volume fraction of oxygen are relatively smaller except for some minor trace species(with a mass fraction of less than 0.1%). In addition，the existing PaSR turbulent combustion model and the pressure-momentum coupling algorithm are also improved and optimized，thereby enhancing their physical accuracy and robustness.

turbulent combustion；local time-stepping method；large eddy simulation；CFL number；OpenFOAM

TK11

A

1006-8740(2021)03-0321-13

10.11715/rskxjs.R2003003

2020-06-20．

国家自然科学基金资助项目(91641110)；国家重点研发计划资助项目(2019YFB1704200).

姚 卫（1983—  ），男，博士，副研究员.

姚 卫，weiyao@imech.ac.cn.

(责任编辑：武立有)