Genomic Predictio of Arsenic Tolerance and Grain Yield in Rice:Contribution of Trait-Specific Markers and Multi-Environment Models

Nourollah AHMADI ,Tuong-Vi CAO ,Julien FROUIN ,Gareth J.NORTON,Adam H.PRICE

(1Institute of Genetic Improvement and Adaptation of Mediterranean and Tropical Plants,French Agricultural Research and International Cooperation Organization,Montpellier F-34398,France;2University of Montpellier,National Research Institute for Agriculture,Food and Environment,French Agricultural Research and International Cooperation Organization,Montpellier SupAgro,Montpellier 34090,France;3School of Biological Sciences,University of Aberdeen,Aberdeen AB24 3UU,Scotland)

Abstract:Many rice-growing areas are affected by high concentrations of arsenic(As).Rice varieties that prevent As uptake and/or accumulation can mitigate As threats to human health.Genomic selection is known to facilitate rapid selection of superior genotypes for complex traits.We explored the predictive ability(PA)of genomic prediction with single-environment models,accounting or not for trait-specific markers,multi-environment models,and multi-trait and multi-environment models,using the genotypic(1600K SNPs)and phenotypic(grain As content,grain yield and days to flowering)data of the Bengal and Assam Aus Panel.Under the base-line single-environment model,PA of up to 0.707 and 0.654 was obtained for grain yield and grain As content,respectively;the three prediction methods(Bayesian Lasso,genomic best linear unbiased prediction and reproducing kernel Hilbert spaces)were considered to perform similarly,and marker selection based on linkage disequilibrium allowed to reduce the number of SNP to 17K,without negative effect on PA of genomic predictions.Single-environment models giving distinct weight to trait-specific markers in the genomic relationship matrix outperformed the base-line models up to 32%.Multi-environment models,accounting for genotype × environment interactions,and multi-trait and multi-environment models outperformed the base-line models by up to 47% and 61%,respectively.Among the multi-trait and multi-environment models,the Bayesian multi-output regressor stacking function obtained the highest predictive ability(0.831 for grain As)with much higher efficiency for computing time.These findings pave the way for breeding for As-tolerance in the progenies of biparental crosses involving members of the Bengal and Assam Aus Panel.Genomic prediction can also be applied to breeding for other complex traits under multiple environments.

Key words:genomic prediction model;genomic selection;complex trait;arsenic tolerance;rice;predictive ability

High concentration of arsenic(As)in rice grains is an important problem in many rice-growing areas(Zavala and Duxbury,2008;Brammer and Ravenscroft,2009;Stroud et al,2011).One of the effective ways of limiting the potential threats to human health is the development of As tolerant rice varieties that limit As uptake and/or translocation to the grains.O.sativaspecies is endowed with a large genetic diversity for As accumulation in the grains when grown under high concentrations of As(Dasgupta et al,2004;Rahman et al,2007;Norton et al,2009,2012a;Frouin et al,2019).Several quantitative trait loci(QTLs)controlling the accumulation of As in rice grains(AsG)were mapped using recombinant inbred lines(Norton et al,2010,2012b;Kuramata et al,2013;Zhang et al,2014).Likewise,a large number of loci associated with AsG were detected with genome-wide association analysis(GWAS)(Norton et al,2014,2019;Frouin et al,2019).Unfortunately,to our knowledge,these findings have not been translated into marker-assisted breeding for As-tolerance in rice so far,probably because of the large number of QTLs involved and their rather small individual effect.For instance,Norton et al(2019)detected 74 QTLs for AsG with individual effect not exceeding 9.9%.

Using a diversity panel of 228 accessions as training set and 95 elite lines as candidate set,Frouin et al(2019)analyzed the predictive ability(PA)of QTLs for AsG detected by GWAS and the PA of genomic prediction.Only 8% of the QTLs detected by GWAS in the training set can be validated in the candidate set,while the PA of genomic prediction for AsG across populations reaches 0.496,indicating that genomic selection(GS)is the most effective molecular breeding option for the improvement of As-tolerance in rice.A reasonably high PA of the genomic estimate of breeding value(GEBV)was obtained in maize(Bernardo and Yu,2007),wheat(Bassi et al,2015)and oats(Asoro,2011).In rice,moderate to high PA of GEBV is achieved for a large set of traits,using different types of references and breeding populations(Ahmadi et al,2020).For instance,Ben Hassen et al(2017)reported the feasibility of accurate GEBV for the progenies of biparental crosses in rice.Ben Hassen et al(2018)reported the higher PA of the multi-environment model,which allows to breed rice simultaneously for productivity and for adaptation to the target abiotic stress when applied to data from managed G × E experiments(E being different levels of a given abiotic stress).Accounting for trait-specific markers improves the PA of GS in rice(Bhandari et al,2019).

This study aimed at evaluating the effectiveness of the above-mentioned options of genomic prediction for the improvement of As-tolerance in rice.Using the publically available large genotypic data and phenotypic data for the Bengal and AssamAusPanel(BAAP)(Norton et al,2018),we explored the PA of genomic prediction for AsG,with single-environment(SE)models,the performances of multi-environment models,and multi-trait and multi-environment genomic prediction models.

RESULTS

SE genomic prediction

PA of genomic predictions in the 144 cross validation experiments involved four levels of linkage disequilibrium(LD)threshold(0.25,0.50,0.75 and 1.00).Three prediction methods [Bayesian Lasso(BL),genomic best linear unbiased prediction(GBLUP)and reproducing kernel Hilbert spaces(RKHS)] and three phenotypic traits [days to flowering(DTF),AsG and grain yield(GY)] were observed under two irrigation systems,continued flooding(CF)and alternate wetting and drying(AWD)over two years,and PA ranged from 0.434 to 0.708,with an overall average of 0.563(Fig.1 and Table S1).Analysis of the sources of variation of PA revealed that among the factors considered,LD threshold and phenotypic traits had highly significant effects.The effects of trait × LD and trait × irrigation-system interactions were also highly significant(Table S2).The least significant difference(LSD)test showed that whatever the trait,the average PA of genomic prediction with LD threshold of 0.25 was systematically lower than that with the other three LD thresholds.Likewise,whatever the trait,the average PA withr2≤ 0.75 was either equal or significantly higher than that with the other LD thresholds,includingr2≤ 1.Average PA for GY was always significantly higher than that for DTF and AsG.Trait × LD interaction was the highest for AsG and GY.The highest trait × irrigation-system interaction was observed for AsG.

Given the systematically high PA obtained with the genotypic dataset selected with LD threshold of 0.75,we decided to use this dataset(17 449 SNPs)for the further analysis.

Genomic prediction accounting for trait-specific markers

The 72 cross validation experiments,involving six weight levels of trait-specific markers(G′0,G′nw,G′0.25,G′0.50,G′0.75,G′1.00)and three phenotypic traits observed under four environments during two years,yielded PA of genomic prediction ranging from 0.480 to 0.792.The overall mean PA was 0.671(Fig.2 and Table S3).Analysis of the variation sources for PA revealed that the effects of trait-specific relationship matrix and phenotypic trait were highly significant(Table S4).Tukey’s honest significant difference(HSD)test showed that inclusion of trait specific markers without specific weight did not significantly increase the PA of genomic prediction.Average PA for G′0and G′nwtreatments were 0.573 and 0.584,respectively(Table S4).HSD test also showed that all G′nwgenomic relationship matrix(GRMs)led systematically to significantly lower PA than GRMs with weighted trait-specific markers(average PA ranging from 0.708 to 0.725).Whatever the environment and the trait,the G′0.50GRM systematically had the highest average PA(0.725)among the four weighted G′w.Likewise,whatever the environment and the trait,the G′1.00had,almost systematically,the lowest average PA(0.708)among the four treatments with weighted specific markers.Among the three traits,DTF was the most sensitive to trait specific markers.Compared to G′0treatment,the average increase of PA for the four GRMs accounting for trait specific markers was 32%for DTF,19% for AsG and 28% for GY.

Fig.1.Predictive ability of genomic prediction in cross validation experiments for arsenic content in grains(AsG),grain yield(GY)and days to flowering(DTF)observed under alternate watering and drying(AWD)and continued flooding(CF)irrigation systems over two years.

Fig.2.Effects of presence and weight of 64 trait-specific markers on predictive ability of genomic prediction for arsenic content in grains(AsG),grain yield(GY)and days to flowering(DTF)observed in four environments.

Fig.3.Predictive ability of genomic prediction experiment with single environment(SE),and multi-environment(ME)models obtained with the genomic best linear unbiased prediction(GBLUP)and reproducing kernel Hilbert spaces(RKHS)statistical methods,for arsenic content in grains(AsG),grain yield(GY)and days to flowering(DTF).

Predictive ability of genomic prediction using multi-environment models

The 72 cross validation experiments involving three levels of models [SE,multi-environment with crossvalidation strategy 1(ME-CV1)and ME-CV2] and two prediction methods(GBLUP and RKHS)yielded PA of genomic prediction ranging from 0.482 to 0.812.The overall mean PA was 0.629(Fig.3 and Table S5).Analysis of the variation sources for PA revealed highly significant effects for model and trait factors(Table S6).Several interactions of order two,including trait × model,and of order three,including trait × model × method,were also significant.The multi-environment model with the ME-CV2 cross validation strategy significantly outperformed SE model with an average gain of PA of 0.182 and 0.161 for DTF,under AWD and CF,respectively.The gain of PA was 0.195 and 0.214 for AsG,and 0.164 and 0.150 for GY under AWD and CF,respectively.On the other hand,the PA obtained with ME-CV1 was not significantly higher than that obtained with SE model.Similar to the trend observed with SE model,the average PA for GY under one of the two ME models was often higher than that for DTF and AsG.The significant effect of trait × model interaction reflected the ability of ME-CV1 to achieve significantly higher PA than SE model for GY,which was not the case for DTF and GY.The trait × model ×method interaction reflected that,under GBLUP method,the ME-CV1 mostly achieved the most discriminant PA among the three traits,while under RKHS method,the most discriminant PA was achieved by ME-CV2(Table S6).

To investigate the possible benefit of a larger number of environments,we implemented the ME-CV2 under GBLUP,while considering each combination of irrigation system and year of experiment as one environment.This provided four environments and allowed predicting traits in each of the four environments while accounting for marker effects in the three remaining environments.Effect of environments on PA was significantly positive(Table S7)but modest,always below 10%(Table S5).Effects of E ×T interaction were also highly significant.For instance,average PA for AsG using four environments was 9%under CF and -3% under AWD.

To investigate the possible benefit of accounting for trait-specific marker in a multi-environment model,we compared the PA of ME-CV2 under GBLUP using a genomic relationship matrix computed with the 17K SNP plus 64 trait-specific markers,the latter either with non-specific weight or with a weight of 0.5(G′0or G′0.50).The effect of trait-specific markers on PA was 4% on average and always below 10%(Table S5),which was significantly positive(Table S8),but very modest.

Table 1.Genetic correlation between days to flowering(DTF),arsenic content in grains(AsG)and grain yield(GY).

PA of genomic prediction using multi-trait &multi-environment models

Whatever the number of environments,genetic correlations between traits were very low and negative between DTF and GY,almost nil between DTF and AsG,very low between AsG and GY(Table 1).The residual correlation between traits was also low,but could reach 80% of the corresponding genetic correlation between traits.In contrast,correlations between environments were high and always above 0.600(Table 2).Joint analysis of the two years’ data markedly improved the correlation between the AWDand CF environments,but not between traits(Tables 1 and 2).

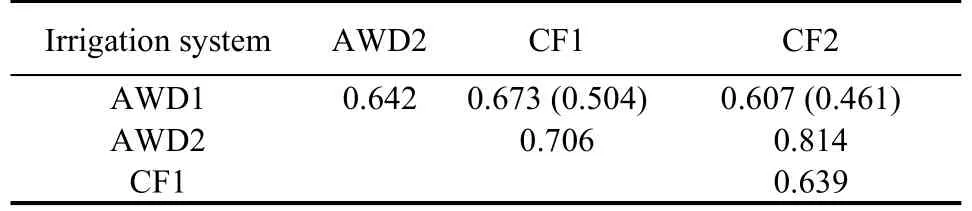
Table 2.Genetic correlation between alternate wetting and drying(AWD)and continued flooding(CF)irrigation systems.

Results after fitting of the Bayesian multi-trait and multi-environment(BMTME)model for the three traits are summarized in Fig.S1.Correlation between the observed and the predicted values are high,0.980 for DTF,0.985 for AsG and 0.950 for GY.Results of evaluation of PA of BMTME model are summarized in Fig.4 and Table S9.Under the four environments,the PA ranged between 0.259 and 0.654 for different combinations of traits and environments.The overall average PA was 0.466.Across the four environments,the largest average PA was 0.514 for DTF,0.370 for AsG and 0.654 for GY.PA was lower option under the two environments than under the four environments,with an average decrease of 10%.

Fig.4.Predictive ability of genomic prediction experiment with three multi-trait and multi-environment prediction models.

PA of the BMORS(Bayesian multi-output regressor stacking)functions under the four environments ranged between 0.688 and 0.839 for different combinations of traits and environments(Table S9).The overall average PA was 0.779.Across the four environments,the largest PA was 0.839 for DTF,0.831 for AsG and 0.785 for GY.The PA achieved with the BMORS function were slightly lower under the two environments than under the four environments,with an average decrease of 4%.Implementation of BMORS_Env function that allows predicting the traits in each environment,using the remaining environments as training,did not improve the function’s PA but increased the standard deviation associated to each PA(Table S9).The overall average PA was 0.744.Across the four environments,the largest PA was 0.835 for DTF,0.792 for AsG and 0.791 for GY.Overall,the BMORS function produced significantly higher PA than the BMTME model and the single-environment models(Table S10).

DISCUSSION

Marker density and use of trait-specific markers

Analysis of the effect of four levels of marker density on the PA of three single-environment genomic prediction models confirmed the superfluity of very dense genotyping when the LD extent is large.Indeed,simulation studies(Habier et al,2009;Zhong et al,2009)and empirical studies in various plant species including rice(ben Hassen et al,2017;Bhandari et al,2019)have shown very little,if any,effect of marker densities,as long as the distance between adjacent markers remains below the extent of LD.Given the size of the rice genome(430 Mb),the theoretical minimum number of markers needed would be 3K evenly distributed SNPs.However,the 4K SNPs dataset(LD threshold of 0.25)led,systematically,to lower PA than the ones with higher numbers of SNPs.This is probably due to the uneven distribution of the SNPs,and the local variation of LD along each chromosome.The 17K dataset(LD threshold of 0.75)provided PA equal to the one observed with the 1600K dataset.Its SNP density compensated for the unevenness of their distribution and for the possible low local LD in each chromosome.

Whatever the size of the genotypic dataset and the phenotypic trait considered,PA obtained with the three prediction methods(BL,GBLUP and RKHS)was not significantly different.Given the fact that several QTLs of rather large effect(up to 5% for DTF,10% for AsG and 25% for GY)were detected in the BAAP population(Norton et al,2018,2019),BL method should perform better than GBLUP and RKHS.This is probably due to the strong linkage of each QTL of rather large effect with a large number of SNPs,taking off the shrinkage edge of BL method.Indeed,the total numbers of SNP associated with DTF,AsG and GY were of 3 515 SNPs,2 720 SNPs and nearly 1 500,respectively(Norton et al,2018,2019).

Exploitation of the results of recent GWAS(Norton et al,2018,2019),via genomic prediction using trait-specific GRM under GBLUP method,was awarded with PA gains ranging from 19% to 32%.Similar gains of PA were reported in dairy cattle for milk yield(Zhang et al,2014)and in rice for traits related to drought tolerance(Bhandari et al,2019).Using GRM built with markers identified through GWAS in Holstein-Friesian bulls,Veerkamp et al(2016)reported no increase in the accuracy of genomic predictions compared to GRM built with a large set of markers including trait-specific SNPs or not.They attributed the finding to the small size of the effective population and the associated long extent of LD.On the other hand,in their study,the share of total phenotypic variance explained by the traitspecific markers did not exceed 19% and they did not attribute a specific weight to those markers.In our study,the share of total variance explained by the trait-specific markers was much higher.For instance,for AsG,the three most important QTLs(represented by 8 SNPs out of the 64 AsG-specific SNPs)each explained 10% to 18% of the total variations.It is also noteworthy that the simple inclusion of the trait-specific SNPs in the genotypic dataset did not improve the PA of genomic predictions.Attribution of a distinct weight is necessary.We empirically opted for four levels of trait-specific weight and,at each level,attributed the same weight to each of the 64 trait-specific SNPs,regardless of the effect of the underlying QTLs.The highest PA for the three triats,for the time trains,was achieved with the trait-specific weight of 0.50.Attribution of weight to trait-specific markers can probably be fine-tuned,by considering the effect of each QTL.

Accounting for G × E interactions and for correlation between traits

The multi-environment models with the ME-CV2 cross validation strategy provided PA gains ranging between 18% and 47% according to traits and environments.Cuevas et al(2016,2017)reported similar higher PA of multi-environment models,compared to single-environment models,using data from multi-local and multi-year trials of maize and wheat.In rice,Ben Hassen et al(2017)reported PA gains of up to 30% by using multi-environment models compared to their single-environment counterparts.Likewise,Bhandari et al(2019)reported PA gains of up to 32% with the RKHS multi-environment models using rice DTF and GY data from three managed drought experiments.In the present study,the two multi-environment models(GBLUP and RKHS)provided similar substantial gains of PA,despite the fact that under the M × E model implemented with GBLUP,the environmental covariance is forced to be positive and constant across pairs of environments.This is probably because correlations between the AWD and CF environments were positive for the three traits over the two years.For instance,in the case of AsG,the correlation between AWD and CF was 0.709 and 0.754 in Year 1 and Year 2,respectively.When the correlation between environments is negligible or negative,the G × E model cannot explain the interaction because the sample correlation is estimated through variance components that are,by definition,all positive or zero.Therefore,the G × E model’s prediction accuracy is similar to that of the single-environment model because the variance of the marker main effects tends to be small and positive.Then,negative correlations between environments are not used to improve the predictions.

PA of the multi-trait and multi-environment model(BMTME),which includes a three-way interaction term(T × G × E)and accounts for correlation between traits,was almost systematically lower than the PA of its single-trait and single-environment counterpart.It was also lower than the PA of the multi-environment models GBLUP and RKHS.This is most probably due to the very low correlation(always below 0.150)between the three traits considered,and the fact that our data did not comply with the hypothesis of unstructured variance-covariance matrix for both genetic and residual covariance matrix between traits.The significantly higher PA,obtained when the model was fitted with the more tightly correlated traits AsG and As in shoot,underline the determining effect of the level of correlation between traits.Similar results were reported by the developers of the BMTME model(Montesinos-López et al,2016),who obtained the highest PA when correlation between traits was above 0.5,in both real and simulated data.

Whatever the trait and the environment,the BMORS function significantly outperformed its BMTME and its single-trait and single-environment models’counterparts implemented with GBLUP method.This is probably because the first stage models of BMORS are simply univariate multi- environment GBLUP that do not use information on correlation between traits,and the second stage models,though based on hypotheses of correlation between traits,does not directly involve a variance- covariance matrix.Instead,it involves an additional training stage where,for each trait,a meta-model is trained with an expanded training set,composed of the input vectors of the first stage,augmented by the estimates of the values of their target variables for all traits,in the first stage models(Spyromitros-Xioufis et al,2016).

Implication for breeding for complex traits

In this study,we found that(I)contrary to widespread idea,more markers is not always better for GS,and the number should be adjusted to LD within the population;(II)combining the QTL models of infinitesimal effects and large effects(i.e.accounting for trait-specific markers)provided better predictions than each of the two models implemented separately;(III)prediction models that account for G × E interactions and/or for correlation between traits achieve higher PA than the conventional single-trait and single-environment models.The three findings applied to both complex traits such as GY and AsG with moderate heritability,and to DTF,a trait of less complex genetic architecture and high heritability.These findings were based on crossvalidation experiments within a diversity panel.Ben Hassen et al(2017)have reported that reasonably high PA of GEBV could be achieved in rice for the progenies of biparental crosses with a reference population composed of a diversity panel that includes the parental lines of those crosses.Thus,our findings would apply,at least,to progeny of crosses between accessions of the BAAP panel for the improvement of grain yield and lowering of grain arsenic in the riceAusgroup.Furthermore,it applies to all crop-breeding programs that have multi-trait and multi-environment targets.

METHODS

Plant materials

A total of 220 accessions belonging to theAusgenetic group ofO.sativawere extracted from theAusdiversity panel of 266 accessions developed by Norton et al(2018)according to the phenotypes(Table S11).

Phenotypic data

Phenotypic data were produced in Mymensingh,Bangladesh during the dry seasons of 2013(Year 1)and 2014(Year 2).Each year,two water management systems,AWD and CF,were conducted.The target traits included DTF,GY and AsG.Details of the phenotyping procedures are provided in Norton et al(2017b,2018).Briefly,in each trial,the experimental design was a randomised complete block with four replicate blocks.The individual plot was composed of one 4 m-long row.At maturity,grains and shoots of each accession were hand-harvested from the six central hills of each row.

Methods for the measurement of AsG are described in Norton et al(2007a,2019).The dried grain powder were digested using nitric acid and hydrogen peroxide and total As content was measured by inductively coupled plasma-mass spectroscopy(ICP-MS).Trace element grade reagents were used for all digests,and certified reference material [Oriental basma tobacco leaves(INCT-OBTL-5)] and rice flour(NIST 1568b)were used for quality control.All samples and standards contained 10 μg/L indium as the internal standard.

Genotypic data and marker selection for genomic prediction

Genotypic data were extracted from the BAAP SNP database,containing 2 053 863 SNPs(Norton et al,2018).Using Gigwa software(Sempéré et al,2019),the BAAP database was filtered for minor allele frequency(MAF ＞ 5%),heterozygosity(H＜5%)and absence of missing data.The filtering yielded 1 603 611 SNPs hereafter referred to as 1600K SNP dataset.BAAP database is available as a project called BAAP at the SNP-Seek database(http://snp-seek.irri.org/).

Using the 1600K SNP dataset,two types of smaller datasets were extracted with the aim of identifying the threshold of marker density below which the accuracy of GEBV declines,and analysing the effect of accounting for trait-specific markers on the performances of genomic predictions.

Four markers’ density levels,corresponding to four LD thresholds(0.25,0.50,0.75 and 1.00),were considered.The 1600K SNP,corresponding to the threshold of 1,was filtered for the remaining three LD thresholds based on the following procedure.First,the 192 trait-specific SNPs were discarded.Then,for each chromosome,the complete pairwiser² matrix was computed.Then,single loci or cluster of loci with pairwise LD with other loci below the threshold was identified.All such individuals were kept,and for each cluster,one locus with the highest MAF was randomly selected.This procedure yielded 17 449,11 677 and 4 255 SNPs for the LD thresholds of 0.75,0.50 and 0.25,respectively.

Selection of trait specific markers was based on GWAS results reported by Norton et al(2018)for DTF and GY,and by Norton et al(2019)for AsG.For DTF,2-3 SNPs were selected along each of the 24 chromosomic segments with ‘notable association’ detected in one of the two years of field experiment;the total number of DTF-specific SNP was 64.For GY,two SNPs were selected at the two extremities of each of the 32 chromosomic segments with ‘notable association’detected in at least one of the two years of field experiment,under at least one of the two water management systems.For AsG,64 SNPs were selected out of the 74 most significant SNPs(P＜0.0001)detected in at least one of the two years of experiment and at least under one of the two water management systems;the remaining 10 most significant SNP were not present in the 1600K SNP dataset.The 192 traitspecific markers are provided in Table S12.

Methods for genomic prediction

Single environment models

Two kernel regression models(GBLUP and RKHS)and a penalised regression model(the Bayesian least absolute angle and selection operator)were used to predict GEBV.Under GBLUP(VanRaden,2008),the genetic effects were considered as strictly additive and the model was fitted using the GRM as kernel matrix in the Gaussian process implemented.RKHS,which dose not rely on formal hypotheses on the type of genetic effects(Gianola and van Kaam,2008),was fitted using the squared-Euclidean distance matrix between accessions(derived from matrix of marker genotypes)as kernel matrix;the bandwidth parameter was equal to 0.5.BL model(Tibshirani,1996;Park and Casella,2008),which hypothesizes most markers have no any effect,applies a strong shrinkage of estimates of marker effects toward zero for markers with small effects.The prior density of marker effects has a Gaussian distribution and,unlike non-Bayesian LASSO,BL imposes no limitation on the number of non-zero regression coefficients.The model was fitted with a formulation where the prior on the regularization parameterλis expressed as aβdistribution that allows expressing vague preferences over a wide range ofλvalues.

Prediction model using trait-specific genomic relationship matrix

Trait-specific GRM(G′)were constructed following the method proposed by Zhang et al(2014).Briefly,it consists in(i)building the standard GRM of Van Raden(2008)(G),with the set of markers that are assumed to have identical small effects not specific to the phenotypic trait considered.(ii)For each trait,building a specific relationship matrix(S),using markers known for their rather large effect on the trait,while specifying the effectwiof each of those markers.(iii)Finally,building for each trait the weighted GRM as:

G′w=W×S+(1 -W)×G

wherewis the overall weight for trait-specific markersw∈[0,1].In this study,the G matrix was built with the 17 449 SNPs dataset(LD threshold of 0.75).For each trait,fourG′WGRM were computed,corresponding towvalues of 0.25,0.50,0.75 and 1.00,while each of the corresponding 64 trait-specific SNPs were given an equal weight,i.e.,0.25,0.50,0.75 or 1.00.The four weighted trait-specific GRMs(G′0.25,G′0.50,G′0.75,G′1.00)were used as kernel in the Gaussian process of implementation of GBLUP in a Bayesian framework.PA of genomic prediction obtained with the fourG′wwas compared to the ones obtained with the standard G matrix computed with 17 449 SNP alone(G′0= G,i.e.w= 0),and with a second G matrix computed with 17 449 SNPs plus the 64 trait-specific SNPs while they were not given specific weight(G′nw).

Multi-environment models

Multi-environment models,used to predict the GEBV with data from AWD and CF irrigation systems,are the above-described GBLUP and RKHS endowed with extensions to include the environmental effects.The extended GBLUP model(Lopez-Cruz et al,2015)separates the effects of each marker into a main effect for all the environments and an effect specific to each environment.The extended RKHS model(Cuevas et al,2017)hypothesizes correlated performances of accessions in different environments and models the genetic correlation between environments with a matrix of orderm×m,mbeing the number of environments.

Multi-trait and multi-environment models

To predict GEBV with data from AWD and CF environments while taking into account the correlation between traits and trait × genotype × environment interaction,we used BMTME developed by Montesinos-López et al(2016),and BMORS function described in Montesinos-López et al(2019).BMTME can be considered as a Bayesian GBLUP for multiple traits and multiple environments using a linear mixed model that includes T × E interaction termed as a fixed effect,and T × G interaction and T × G × E interaction termed as random effects,assuming independence between environments.BMORS function does not specify the T × E interactions in a variance-covariance matrix.Instead,using the multi-target regression approach(Spyromitros-Xioufis et al,2016),it relies on a meta-model.First,for each trait,a multi-environment GBLUP model is implemented.Then,a meta-model is implemented to scale the predictions of the first-step model.Each meta-model is implemented with a mixed model where the covariates represent the scaled predictions of each trait obtained with the GBLUP model of first-step analysis.The scaling of each prediction is performed by subtracting its mean and dividing it by its corresponding standard deviation.

Computing predictive ability of genomic prediction

Genomic prediction with single environment models was performed using phenotypic data from each combination of irrigation system and year of field experiment,hereafter referred to as AWD1,AWD2,CF1 and CF2.The crossvalidation scheme used 80% of the accessions(176 accessions)as the training set and the remaining 20%(44 accessions)as the validation set.

Multi-environment models were fitted separately for data from Year 1 and Year 2.In each case,PA was computed with two cross-validation schemes.Under the first scheme(CV1),individuals serving as training set were all endowed with phenotypic data from the two environments while phenotypic data were lacking for all the individuals included in the validation set.Under the second scheme(CV2),however,individuals in both the two sets were endowed with at least one phenotypic data in at least one environment.

BMTME model and the BMORS function were fitted first with data from Year 1 and Year 2 separately,then with data from the two years jointly.Cross validations were performed with only the CV2 method.

For all models,cross-validation consisted in one hundred replicates of the random partitioning of accessions into training and validation sets.For each partition,the Pearson correlation coefficient between the predicted and the observed phenotypes in the validation set was computed.Then,PA of genomic prediction was computed as the average of the 100 replicates of the correlation coefficients.The standard error associated to each PA was also calculated.For the multi-environment models,the correlation was calculated within each environment.The same partitions were used under both GBLUP and RKHS models to compute the PA for DTF,AsG and GY.All models were fitted with 25 000 iterations for the Gibbs sampler and 5 000 burn-ins.In the case of BMTME,which requires very long computing time,the cross-validation was performed with 5 000 iterations and 1 500 burn-ins.

Variance of the computed PA was partitioned into different sources through ANOVA after transformation of the correlation coefficient data into a Z-statistic [Z= 0.5[ln(1 +r)- ln(1 -r)]].The Z-statistic was transformed back torvariable after ANOVA.

Implementation of the models

The single environment models and the multi-environment were implemented in the R-3.4.2 environment with the R packagesBGLR1.0.5(Pérez and de los Campos,2014).The multi-trait and multi-environment models BMTME and BMORS were implemented in the R-3.6.1 environment with the R package BMTME(Montesinos-López et al,2019).The analyses were supported by the CIRAD-UMR AGAP HPC Data Centre of the South Green Bioinformatics platform(http://www.southgreen.fr/).

SUPPLEMENTAL DATA

The following materials are available in the online version of this article at http://www.sciencedirect.com/journal/rice-science;http://www.ricescience.org.

Fig.S1.Graphic representation of the predicted values of three phenotypic traits by Bayesian multi-trait and multienvironment model against their observed values.

Table S1.Predictive ability of genomic prediction with single environment models.

Table S2.ANOVA on predictive ability of genomic prediction with single environment models.

Table S3.Predictive ability of genomic prediction models accounting for trait-specific markers.

Table S4.ANOVA on predictive ability of genomic prediction with different weight given to trait specific markers.

Table S5.Predictive ability of single-environment and multienvironment prediction models.

Table S6.ANOVA on predictive ability of genomic prediction with single environment and multi-environment models.

Table S7.ANOVA on predictive ability of genomic prediction of multi-environment models.

Table S8.ANOVA on predictive ability of genomic prediction with multi-environment models and trait specific markers.

Table S9.Predictive ability of genomic prediction with multitrait and multi-environment models.

Table S10.ANOVA on predictive ability of genomic prediction with multi-trait &multi-environment models.

Table S11.Phenotypic data of 220 accessions of the Bengal and AssamAusdiversity panel.

Table S12.SNPs associated with the most significant QTLs for the three traits identified by genome-wide association analyses.