分形纳米毛细管中水的有效渗透率
王桂芹,周蔚怡,宜海友,崔亮靓,许 步,戴昌润,洪鑫文,纪晶文
(1.延安大学 石油工程与环境工程学院;2.延长油田股份有限公司 注水项目区管理指挥部,陕西 延安 716000)
页岩储层通常包含非常窄的纳米尺度孔隙通道[1],水平井钻井和多级滑溜水压裂是目前开发页岩油气资源的关键技术[2]。返排压裂液是水力压裂过程的最后一步,一些研究人员指出,只有不到50%的注入压裂液可以回收。裂缝网络中滞留的水通过自吸作用进入封闭的纳米孔,是造成油气采收率低的主要原因[1,3]。更好地理解纳米尺度孔隙中的滑溜水流动行为对预测非常规油气藏的采收率是至关重要的[4]。
Lucas和Washburn建立了毛细管驱动液体进入均匀截面毛细管的经典解析解[5]。有几位研究者应用了Lucas-Washburn方程(L-W方程)直接研究渗吸现象[6]。然而,上述研究基于无滑移边界条件的基本假设,即近壁流体层速度为零。事实上,一些含气/油的页岩地层孔隙的半径比含水的孔隙大10-100倍。很明显,观测到的结果与无滑移边界条件下的预测结果有相当大的出入[7]。一些研究者指出,页岩和其他多孔介质遵循分形尺度规律[8-10],而分形理论因其能够代表这些分形多孔介质的自相似性孔隙结构及其流动能力而受到关注[11-14]。纳米孔中流体流动存在多重流动机理。亲水性纳米孔中,近壁面区域的承压水有效粘度高于散装水。然而,水分子可以有效地沿着疏水纳米孔壁流动,无滑移边界条件滑动假设不再成立[15]。此外,承压水流动行为主要是由水/纳米孔壁相互作用影响,水/壁相互作用发生在分子水平上。具有不同孔径的多孔介质可以看作是一束弯曲的、截面面积可变的毛细管,弯曲毛细管的长度服从分形定律[16,17]。本文充分考虑水在页岩纳米孔中流动时的不同流动机理,并结合页岩纳米孔的分形特性,研究水在纳米毛细管中的流动特性。
1 水在纳米毛细管中流动的分形模型
1.1 流量
Zeng等人充分考虑滑溜水压裂液在页岩纳米管中流动的多种流动机理,建立了水在单根直纳米毛细管中流动时的统一流量方程[4]:
(1)
式中:q为单根纳米毛细管中液体流动时的体积流量,m3/s;λ为纳米毛细管孔隙的直径,m;ΔP是施加在纳米毛细管两端的压降,Pa;L0为纳米毛细管通道的直线长度,m;μb为水的体相粘度,Pa·s;ls为水在纳米毛细管中流动时的真实滑移长度,m。
真实滑移表示流体分子有效地沿壁面滑动,在一定条件下,滑移长度可以通过任意给定液体的接触角计算得到[15]:
ls=C/(cosθ+1)2,
(2)
C是一个常数,m;θ是接触角。
由于近壁面受限水的粘度与体相水的粘度相差很大,导致水/水界面会出现明显的滑移[18]。在实际应用中,考虑真实、明显滑移效应的约束流体滑移长度应替换为有效滑移长度Lse,其表达式为[15]:
(3)
式中:Lse是有效滑移长度,m;Lsa为表观滑移长度,m;μb为水的体相粘度,Pa·s;μd为承压流体的有效粘度,Pa·s。
承压流体的有效粘度强烈地依赖于体相流体和界面层流体的粘度。承压水的有效黏度可由块状区域的水黏度与纳米孔界面水黏度的组合表示[19]:
(4)
式中:μd为承压水的有效粘度,Pa·s;μi为界面区流体粘度Pa·s;Aid是界面层的面积,m2;Atd是纳米孔隙的横截面积,m2。
(5)
式中:λc为承压流体临界厚度,m。
界面区域的水粘度可表示为[15]:
μi=(-0.018θ+3.25)μb。
(6)
体积水粘度是温度的函数[15]:
μb=
(7)
式中:T是水的温度,K;该公式适用于温度范围为273.15 K~423.15 K。
在页岩储层纳米毛细管中,真实纳米毛细管长度与毛细管直径满足如下分形关系[16,17]:
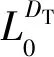
(8)
式中:Lt为页岩储层纳米毛细管通道的实际长度,m,且Lt≥L0;DT为页岩储层纳米毛细管的迂曲度分形维数,1 考虑到页岩储层纳米孔隙的分形特征,采用纳米毛细管的实际长度,以及水在纳米毛细管中流动的流动机理,式(1)可改为: (9) 由式(8)和式(9)可得: (10) 式(10)即为水在单纳米毛细管中流动时流量方程的分形表达式。可以看出分形流量方程即是水在纳米孔隙毛细管中各种流动特征(速度滑移、边界层)的函数,也是毛细管结构特征(孔隙直径、迂曲度分形维数)的函数。式(10)中,忽略水在纳米孔中流动的各种流动机理,即可得纳米毛细管中不考虑水流动的各种流动机理的分形流量表达式: (11) 式(11)中,当DT=1时,分形流量方程简化为哈根-泊谡叶方程: (12) 页岩基质纳米管中流体流动时仍满足广义达西定律: (13) 由式(10)和式(13),可得分形纳米毛细管中水的有效渗透率: (14) 式(14)即为水在页岩纳米毛细管中流动的有效渗透率的分形模型。不考虑水在纳米管中的速度滑移、边界层流体粘度变化等流动机理,即可得纳米毛细管中水的有效渗透率的分形模型: (15) 式(15)中,当DT=1时,分形有效渗透率方程简化为Corey-Zemany方程: (16) 不考虑水的粘度随压力和温度变化,可以令有机孔接触角θOM=60°,θIOM=150°,T=300 K,C=0.41×10-9m,λc=0.7×10-9m,L0=5×10-9m。 令纳米毛细管直径为100 nm,图1给出了纳米毛细管中水的流量(10)式随纳米毛细管两端压力梯度和毛细管迂曲度分形维数的变化趋势。由图1可知,毛细管两端压力梯度越大,纳米毛细管中水的流量越大;而页岩储层纳米孔隙迂曲度分形维数越大,水的流量就越小。即纳米孔隙弯曲程度越大,水在其中流动时受到的阻力就越大,从而会使得纳米孔自吸能力变差,压裂液返排率就会变高。同时,从图1还可以看出在相同孔隙直径和压力梯度条件下,有机纳米毛细管的自吸能力高于无机纳米毛细管,这是由于孔隙不同润湿性所致。疏水性有机纳米毛细管中的滑移长度大于亲水性无机纳米毛细管;同时,疏水性边界层水的粘度低于体相粘度,而亲水性无机纳米毛细管中边界层的粘度高于体相流体粘度。 令纳米毛细管两端压力梯度为2.07 Pa,图2给出了页岩纳米毛细管中水的有效渗透率随毛细管直径和毛细管迂曲度分形维数的变化趋势。由图2可知,页岩基质纳米孔隙直径越大,水在其中流动时的有效渗透率就越大;而页岩基质纳米孔隙分形维数越大,水在其中流动时的有效渗透率就越小。在孔隙直径相同的条件下,水在疏水性有机纳米毛细管中流动时的有效渗透率大于亲水性无机纳米毛细管中的有效渗透率。与流量特征一致,亦是由于纳米孔隙不同润湿性所致。 a.分形有机毛细管 充分考虑水在页岩纳米毛细管中的各种流动机理以及页岩基质纳米孔隙的分形特征,建立了水在纳米毛细管孔隙中流动的流量和有效渗透率的分形模型。通过分析可知,毛细管两端压力梯度越大,纳米毛细管中水的流量越大;而页岩基质纳米孔隙迂曲度分形维数越大,水的流量就越小。水在疏水性有机纳米毛细管中流动时的流量和有效渗透率均大于亲水性无机纳米毛细管。多级滑溜水压裂是目前开发页岩油气资源的关键技术,裂缝网络中滞留的水通过自吸作用进入封闭的纳米孔,充分考虑页岩基质的分形特征对于预测非常规油气藏的采收率是至关重要的。1.2 有效渗透率
2 结果与讨论
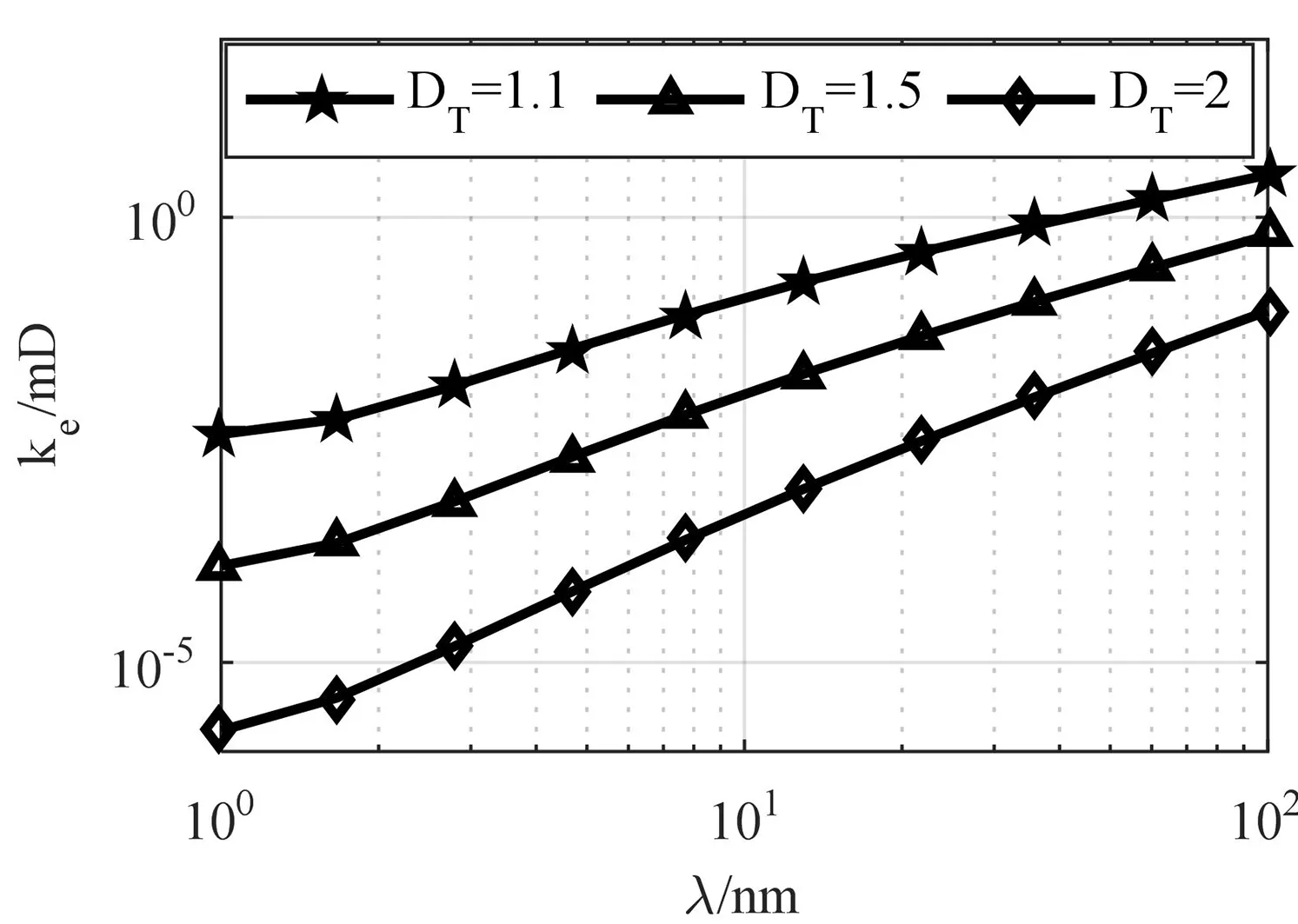
3 结论

