基于改进正弦余弦算法的WSN分簇路由协议
和 煦,宁中正,杨小勇
(1.西安邮电大学 通信与信息工程学院,陕西 西安 710121; 2.国家无线电频谱管理研究所,陕西 西安 710061)
无线传感器网络(Wireless Sensor Network,WSN)是在监测区域范围内部署大量能量有限的传感器节点,并以无线通信方式形成的自组织网络系统[1],其在军事、农业、医疗以及智能家居等方面都有广泛的应用。但是,存在的主要问题之一是在能量有限的情况下延长网络的生命周期[2]。考虑路由协议是WSN能耗的主要构成[3],因此通过优化路由协议延长网络的生命周期是一种重要且高效的节能方式。
低功耗自适应集簇分层型(Low Energy Adaptive Clustering Hierarchy,LEACH)协议是最经典的路由协议,其将整个网络的生命周期分为多个轮,在每轮中先随机选举簇头,簇头接收簇内所有成员节点采集的环境检测数据,进行数据融合,再传输到基站。考虑簇头选举的随机性,容易导致能量较低的节点被选为簇头且不能均匀分布在整个网络中,出现网络能耗不均衡现象[4]。针对经典LEACH协议簇头选举的不足,文献[5]提出了一种自适应簇头轮换机制,提高了网络寿命和能量利用率。文献[6]提出了一种改进的路由协议,采用节点的剩余能量、邻居节点的个数以及与基站之间距离这3个因子改进阈值的计算公式,有效降低了网络的能量消耗。文献[7]提出了一种能量均衡的成簇协议,分别对成簇阶段的簇头选举公式和稳定阶段的通信周期进行了改进,平衡了整个网络的能量消耗。此外,国内外学者也在一些群体智能优化算法的基础上提出了各类改进的分簇路由协议,如基于引力搜索算法的分簇路由协议[8],采用引力搜索算法对网络簇头的通信链路进行规划,同时,根据普通节点与高能节点能量的差异进行分簇,较好地均衡了节点的能耗。基于粒子群优化算法的分簇路由协议[9],利用粒子群优化算法选出最优簇头,提高了网络寿命。基于萤火虫算法的分簇路由协议[10],通过自组织映射神经网络和萤火虫算法求最优解,从而获得合适的分簇,在一定程度上改善了网络存活时间,但是上述研究在分簇阶段均未考虑簇头与基站之间的距离因素,簇头传输数据到基站可能消耗较多的能量。
针对经典LEACH协议中随机选举簇头的不足,拟提出一种基于改进正弦余弦算法的分簇路由协议(Clustering Routing Protocol Based On Improved Sine Cosine Algorithm,CRISCA),引入惯性权重因子改进正弦余弦算法,并在簇头选举时,综合考虑各节点之间、节点与基站之间的距离以及节点的剩余能量因素构建适应度函数。通过求得适应度函数的最优解选举最优簇头,降低节点的能耗,延长网络的生命周期。
1 系统模型
1.1 能耗模型
采用文献[11]中常用的一阶无线电模型作为该WSN的能耗模型,如图1所示。
当发送数据为l,传输距离为d时,能量消耗公式为
(1)
(2)
接收lbit数据时的能量消耗公式为
ER(l)=lEe
(3)
若某簇内节点总数为n,每个节点传输lbit数据到簇头时,簇头数据融合的能量消耗公式为
EF(l,n)=nlEf
(4)
其中:Ee为传感器处理单位数据时的能量消耗;εs和εm分别为自由空间模型和多径衰落模型中功率放大器能量消耗的比例系数;d0为距离阈值;Ef为数据融合的能耗系数。
1.2 网络模型
网络模型由一个基站、多个簇头节点以及多个成员节点组成,分簇网络模型如图2所示。
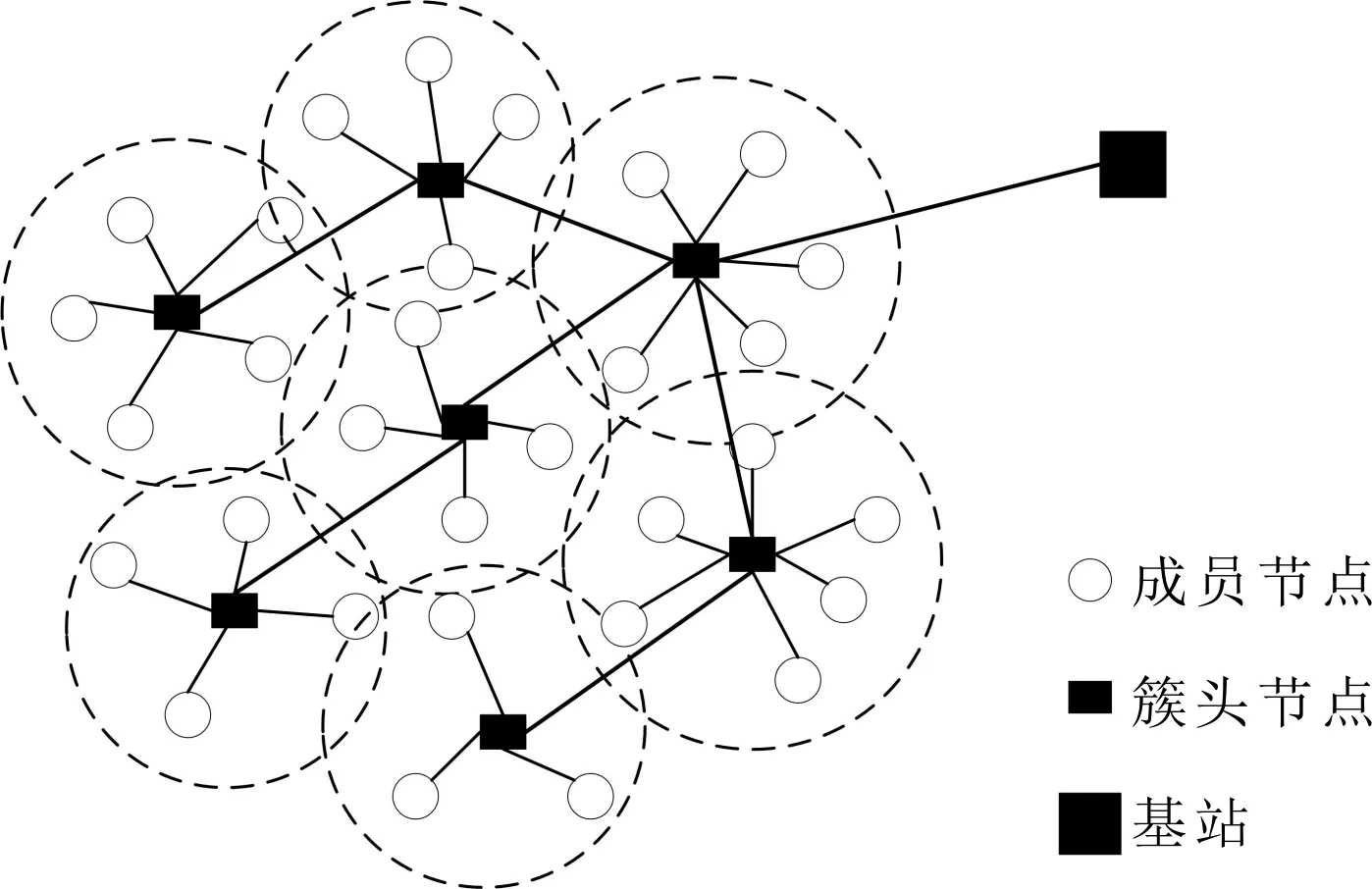
图2 分簇网络模型
对分簇网络做如下规定。
1)所有节点的初始能量均相同,且不能补充能量,基站的能量视为无限。
2)所有节点都具有唯一的身份标识号(Identity Document,ID),且均有可能成为簇头。
3)所有节点和基站部署之后均不能改变位置,但能感知接收信号的强度计算彼此之间的距离。
4)簇头节点接收簇内所有成员节点采集的检测数据,并对这些数据进行融合,传输到基站。
2 正弦余弦算法
2.1 标准的正弦余弦算法
正弦余弦算法[12](Sine Cosine Algorithm,SCA)是一种新的群体智能优化算法,具有参数少、结构简单以及易实现等特点,因此,利用正弦和余弦函数的波动性和周期性进行迭代寻优。假设种群规模为M,即包含M个个体,每个个体的维度为D,那么,个体i在第j维的空间位置表示为Xij,i∈{1,2,…,M},j∈{1,2,…,D}。首先,在解空间内随机产生M个个体的初始位置,对应种群规模的大小。然后,计算每个个体的适应度值,并记录当前最优个体位置。最后,循环至满足终止条件,输出最优解。在每次迭代中,个体位置的更新表达式为
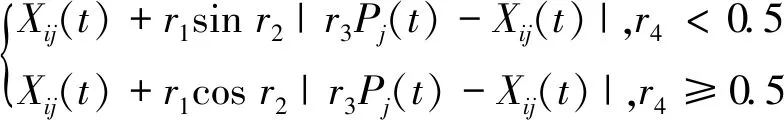
(5)
其中:Xij(t)为个体i在第t次迭代时的位置在第j维的分量;Pj(t)为第t次迭代种群当前最优个体在第j维的分量;r2∈[0,2π]、r3∈[0,2]和r4∈[0,1]为3个随机参数;r1为控制参数,随着迭代次数的增加从a递减到0,可表示为
(6)
其中:a为常数;t为当前的迭代次数;T为最大迭代次数。
2.2 改进的正弦余弦算法
惯性权重主要控制历史因素对当前状态的影响程度[13]。标准的SCA中惯性权重默认为1,导致算法在迭代初期保持较大范围的全局搜索,而在后期搜索个体易发生位置的震荡。
给每次迭代的所有个体分别引入不同大小的惯性权重,按照每个个体的适应度函数值进行从小到大的排序,适应度值越小表明个体离最优位置越近,此时让个体拥有较小的惯性权重,增强局部搜索能力。反之,适应度值越大表明个体离最优位置越远,此时让个体拥有较大的惯性权重,增强全局搜索能力,让个体向最优位置靠近。同时,采用0~π/2之间的余弦函数控制惯性权重的变化,该函数在该区间内是单调递减的,且在初期的递减速度较慢,能保证搜索初期保持较大的惯性权重,且不会过早进入局部搜索,避免早熟,后期保持较小的惯性权重。此惯性权重表示为
(7)
其中:wmax和wmin分别为惯性权重的最大值和最小值;orderi为第i个个体按适应度值由小到大排序的索引。因此,改进的正弦余弦算法(Improved Sine Cosine Algorithm,ISCA)的位置迭代方程由式(5)更新为
Xij(t+1)=
(8)
3 基于ISCA的分簇路由协议
经典LEACH协议主要依据各传感器节点产生一个(0,1)之间的随机数是否小于所设的阈值进行簇头的选举[14],但是这种随机选举簇头的方式容易导致能量较低的节点被选为簇头和簇头分布不均匀现象。在经典LEACH协议的基础上采用ISCA算法,依据各节点之间、节点与基站之间的距离以及节点的剩余能量构建适应度函数,确定每轮最佳簇头的选举方案。
3.1 簇头初始化
在ISCA中,采用随机方式选取候选解集,而经典LEACH协议也采用随机方式选举簇头,容易导致算法陷入局部最优,选举能量较低的节点成为簇头节点,导致簇头过早死亡。为此,在初始化时,对候选簇头节点的能量进行一定的限制。
假设网络覆盖区域范围内传感器节点总数为N,每轮在其中选举G个簇头,基站根据所有节点的能量信息,计算当前剩余能量最大的节点,并从其余节点中选取能量大于或等于最大能量一半的节点构成一个集合,即
A={E(k):E(k)≥0.5Ekmax|∀k,1≤k≤N}
再从集合A中随机选取G个节点构成一个个体,随后采用同样的方法继续在集合A中选取G个节点,一共进行M次选取,最终生成M组初始簇头节点集,即M个个体。每个个体代表一种簇头的选举方案,个体的维度D均相同,且等于簇头的数量G,通过适应度函数评价解的质量,选取最大迭代次数后的最优个体,对应簇头的最佳选取方案。
3.2 适应度函数
簇头节点主要负责簇内成员节点的数据收集和融合,再将融合后的数据传送到基站,因此,簇头节点为网络中的关键节点,比成员节点消耗更多的能量[15]。基于这一特点,将簇头节点与成员节点之间的距离,与基站之间的距离以及自身的剩余能量这3个因素加入适应度函数的构建中,作为簇头选举的评价指标,此适应度函数方程组表示为
(9)
其中:f1为成员节点nk到对应簇头hip的最大平均欧式距离因子,hip为第i个个体中的第p个簇头,|cip|为簇头hip中包含成员节点的总数;f2为簇头hip与基站b之间的距离因子;f3为簇头hip剩余能量的比重因子;λ1,λ2,λ3分别为各因子的权重值,且λ1+λ2+λ3=1。
f1的值越小,说明簇内成员节点到簇头的平均距离越小,整个簇越紧凑,成员节点传送数据到簇头时将消耗较少的能量;f2的值越小,说明较多簇头分布在离基站较近的位置,簇头传送数据到基站时将消耗较少的能量;f3的值越小,说明簇头的能量比重越大,较高能量的节点被选为簇头的可能性越大。
将每个个体的位置代入到式(9)的适应度函数中,通过ISCA求解在最大迭代次数之内,适应度函数的最小值,这个最小值对应的解就是最优解,也就是最优个体位置。因此,使适应度函数f值最小的个体所包含的簇头性能最好,个体的各维度分量对应此轮中各簇头的位置。
3.3 基于ISCA优化簇头选举的具体步骤
通过ISCA求解适应度函数f的最优解,得到每轮的最佳簇头选举方案,具体流程如图3所示。
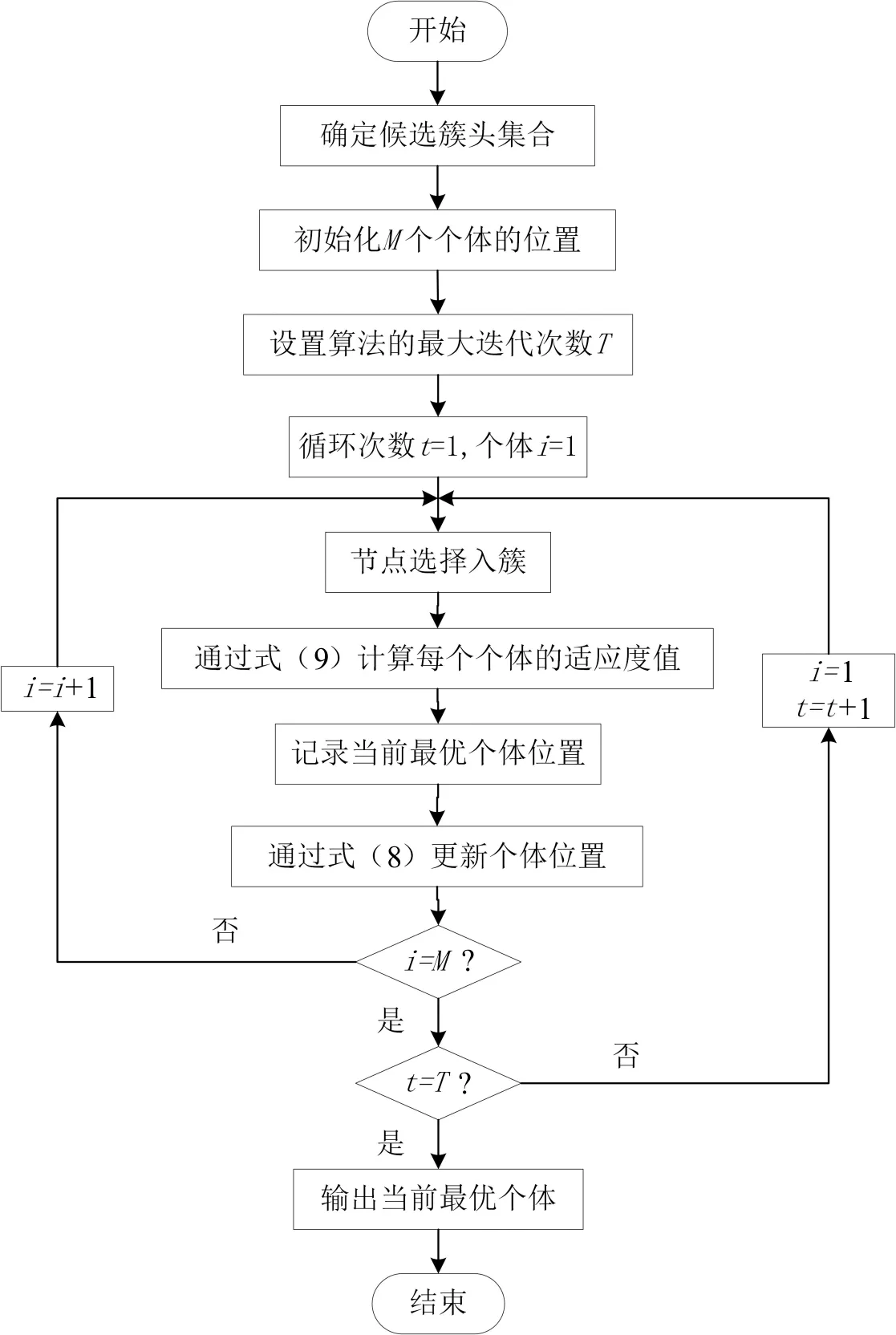
图3 ISCA优化簇头选举的流程
具体步骤如下。
步骤1计算当前剩余能量最大的节点,并选取剩余能量大于或等于最大剩余能量一半的节点,将其作为候选簇头集合。
步骤2初始化M个个体,每个个体包含G个候选簇头节点,即每个个体代表一种簇头的选举方案,同时,设置算法的终止条件和最大迭代次数T等参数。
步骤3对于每个个体,计算网络中所有成员节点到每个个体中簇头节点的距离,并选择最短距离的簇头入簇。
步骤4通过式(9)计算每个个体的适应度值,并记录当前最优个体位置。
步骤5通过ISCA算法的位置更新式(8)个体的位置。
步骤6判断是否满足终止条件,若满足,则输出当前最优个体,最优个体中各维度的分量对应各簇头节点的位置,否则重复步骤3-步骤5。
4 算法仿真与分析
4.1 仿真环境设置
所有的仿真均采用MATLAB 8.5软件编程,在Intel Core i7 CPU,8 GB内存,2.6 GHz主频的计算机上实现。在200 m×200 m的网络覆盖区域内随机布设200个传感器节点,基站的坐标为(100,250)m,簇头的选举概率为0.05,各节点的初始能量均为0.5 J,数据包大小为4 kB,控制包大小为100 B,Ee=50 nJ·bit-1,Ef=5nJ·bit-1,εs=10 pJ·(bit·m2)-1,εm=0.001 3 pJ·(bit·m4)-1。算法的最大迭代次数T为20,种群规模M为15,路由协议更新的最大轮数rmax为1 100轮,最大惯性权重和最小惯性权重分别为1.0和0.3,常数a取值为2;λ1、λ2、λ3的取值分别为0.35、0.35、0.3。
4.2 仿真结果与分析
为了对CRISCA协议的优化性能进行评估,在WSN的各参数均相同的前提下,将该协议与经典LEACH协议进行对比仿真,观察不同轮次中存活节点数的对比。将网络生命周期分为稳定周期和生存周期。稳定周期定义为网络开始工作到第一个节点死亡的时间间隔,生存周期定义为网络开始工作到80%节点死亡的时间间隔,即对应第160个节点的死亡轮数。网络中各节点和基站的初始分布如图4所示,图5和图6分别是LEACH协议和CRISCA协议运行到800轮的各节点分布状态。

图4 网络中节点和基站的分布情况
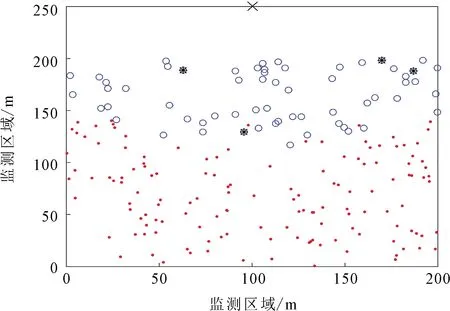
图5 LEACH协议运行到800轮节点的分布状态
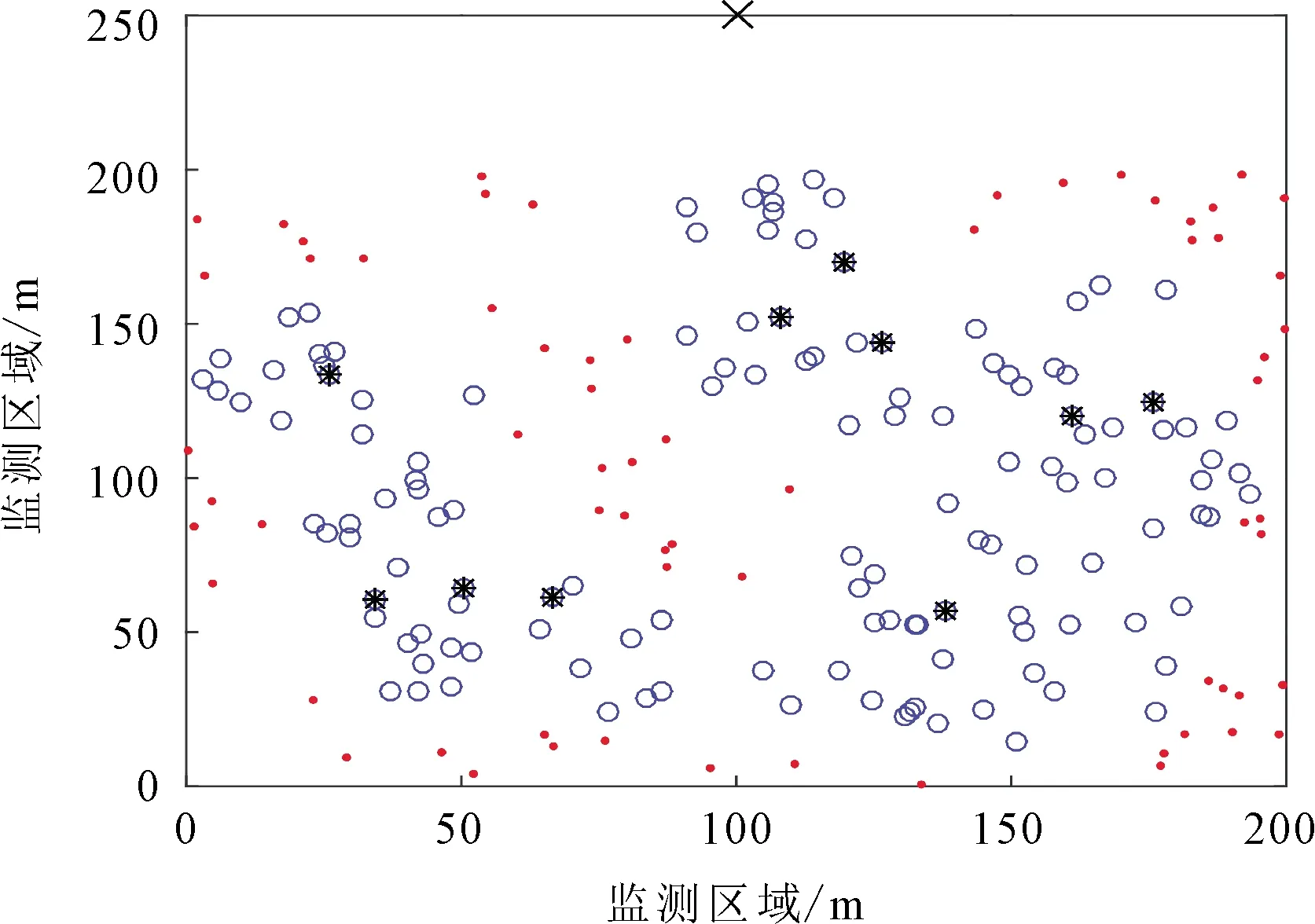
图6 CRISCA协议运行到800轮节点的分布状态
图4-图6中圆圈代表存活节点,带星号的圆圈代表簇头节点,圆点代表死亡节点,叉号代表基站。可以看出,运行到800轮时,LEACH协议中死亡节点都分布在离基站较远的区域,且分布较集中,出现能耗不均衡现象。而CRISCA协议中死亡节点分布较均匀,网络能耗较均衡。此外,LEACH协议和CRISCA协议的死亡节点个数分别为139个和67个。与LEACH协议相比,CRISCA协议将死亡节点的数目降低了51.80%。
图7是网络生命周期对比情况,由图7可以看出,所提CRISCA协议的第一个节点的死亡时间为第493轮,而经典LEACH协议的第一个节点的死亡时间为第311轮。相对于LEACH协议,CRISCA协议将网络的稳定周期提高了58.52%;同时,CRISCA协议的第160个节点的死亡时间为第1 008轮,而经典LEACH协议的第160个节点的死亡时间为第839轮。相对于LEACH协议,CRISCA协议将网络的生存周期提高了20.14%。因此,所提的CRISCA协议相对于经典LEACH协议有效延长了网络的生命周期。
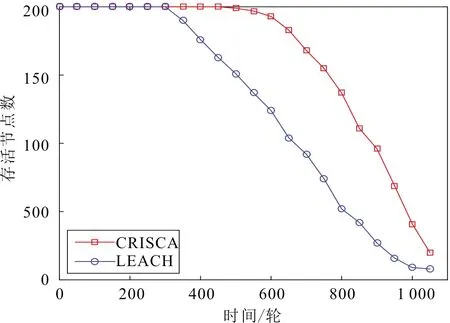
图7 网络的生命周期对比
5 结语
针对经典LEACH协议中簇头选举的随机性,提出一种基于改进正弦余弦算法的WSN分簇路由协议CRISCA,设计了关于节点的位置和能量的适应度函数,采用ISCA得到适应度函数的最优解,从而确定每轮的最佳簇头选举方案。仿真结果表明,CRISCA协议能较明显地减少了WSN能量的消耗,延长了WSN的生命周期。

