空间和光谱信息保持的多光谱图像融合算法
黄峰, 黄伟蓝, 吴衔誉
(福州大学机械工程及自动化学院, 福建 福州 350108)
0 引言
多光谱图像是由多张光谱波段不同, 但空间分辨率相同的灰度图像组成的数据立方体, 其在地物分类、 地质调查以及环境质量监测等方面具有广泛的应用. 但是受多光谱成像器件硬件条件的限制, 多光谱成像传感器往往只能获取到低空间质量的多光谱图像, 而由全色图像传感器所获取的全色图像具有高空间分辨率. 为了获得高空间质量的多光谱图像, 将多光谱和全色图像进行融合, 可实现优势互补, 在尽量保持多光谱信息的前提下, 提升融合图像的空间质量.
现有的多光谱图像融合方法有成分替换法(component substitution, CS)、 多分辨率分析法(multi-resolution analysis, MRA)、 贝叶斯法和基于深度学习的方法. CS方法是指对多光谱图像进行投影, 以分离空间和光谱信息, 然后将包含空间信息的部分替换为全色图像, 主要包括IHS[1]、 PCA[2]、 GS[3]、 AIHS[4]等, 该方法运算耗时少, 但融合图像易产生谱失真现象; MRA方法通过滤波将全色图像的空间信息注入多光谱图像, 主要包括Laplacian Pyramids[5]、 Wavelet[6]、 Discrete Wavelet Transform[7]等, 该方法运算速度快且谱失真现象有所改善, 但可能会出现空间结构失真的问题; 贝叶斯方法[8-10]用最大化后验概率的思路或变分的数学方法来建模, 能降低融合问题的病态程度, 但运算耗时长; 基于深度学习的方法[11-12]需要大量的数据训练模型, 限制了该方法在多光谱图像融合方面的应用.
上述融合方法存在如下两个问题: 第一, 不能很好地描述多光谱与全色图像之间的结构相关性, 造成空间结构失真; 第二, 不能很好地保持多光谱图像的光谱信息, 造成光谱失真. 为了解决第一个问题, 本研究采用边缘自适应提取约束项和线性组合系数约束项来改善融合图像的空间质量; 为了解决第二个问题, 研究采用光谱信息保持约束项和波段比例关系保持约束项来保持多光谱图像的光谱质量. 联立以上4个约束项, 即4个能量泛函, 建立总能量泛函, 使用梯度下降法进行求解, 从而得到最优值, 即最终的融合图像.
1 约束项
本文方法主要基于以下4个约束项: ① 从全色图像中自适应提取边缘细节信息并注入多光谱图像中, 以建立边缘自适应提取约束项, 获得第一个能量泛函; ② 根据全色图像是融合图像各波段的线性组合的假设, 估计多光谱图像各波段线性组合系数, 以建立线性组合系数约束项, 获得第二个能量泛函; ③ 根据低空间分辨率多光谱图像是由融合图像经过模糊和下采样处理后得到的假设, 建立光谱信息保持约束项, 获得第三个能量泛函; ④ 根据融合前后多光谱图像波段比例关系一致可减轻光谱失真的假设, 建立波段比例关系保持约束, 获得第四个能量泛函. 将以上4个能量泛函合并到一个变分框架中, 从而获得一个总的能量泛函.
1.1 边缘自适应提取约束
传统的多光谱图像融合算法通过将全色图像的边缘信息注入多光谱图像, 从而获得具有高频细节信息的融合图像. 但当注入的边缘信息较少时, 会造成融合图像细节信息模糊, 当注入的边缘信息过多时, 则会造成融合图像光谱失真. 本研究采用自适应提取边缘方法[4]来控制注入多光谱图像的边缘信息量, 即
Fi(x)=Mi(x)+h(x)(P(x)-I(x))
(1)

(2)
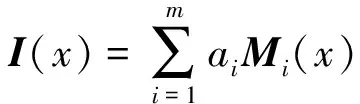
(3)
其中:x为像素位置,x∈Ω,Ω∈Rn为开放有界区间域;Mi为第i个波段的多光谱图像;ai=1/m;I表示多光谱图像的平均灰度;P为全色图像; ▽P为全色图像的梯度;ε为控制分母非零的小值;v为权衡参数, 控制全色图像边缘信息的注入量;h(x)为边缘检测函数, 用来控制注入的边缘信息量(P-I);Fi为第i个波段的融合图像, 1≤i≤m.
由式(1)得到的能量泛函为

(4)
1.2 线性组合系数约束
全色图像可以看作融合图像各波段的线性组合[8], 但线性组合系数如果相同, 则不能很好地表达多光谱图像与全色图像之间的结构相关性. 为避免空间结构失真, 本研究采用自适应估计线性组合系数方法[4]计算线性组合系数αi, 即
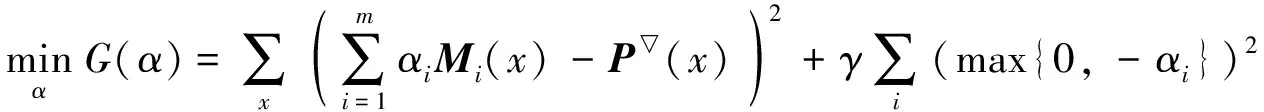
(5)

(6)
其中:αi为第i个波段的线性组合系数, 1≤i≤m;P▽为降质后的全色图像.
式(5)的第一项保证产生的系数组合{α1, …,αi, …,αm}近似融合图像各波段的线性组合; 第二项保证求得的系数αi是非负的,γ为拉格朗日乘子.使用梯度下降法求解式(5), 即
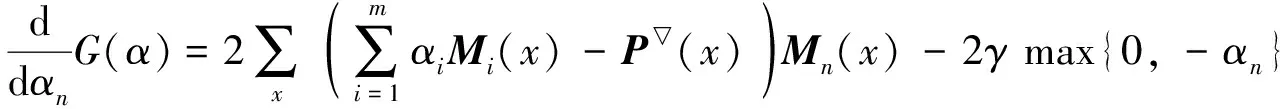
(7)
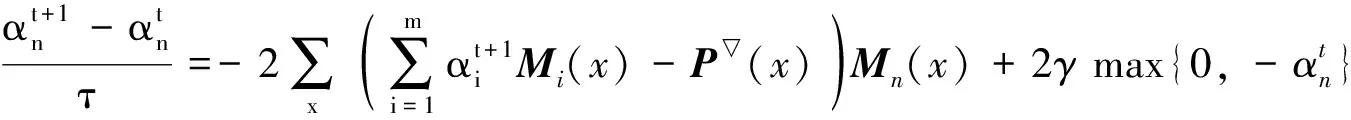
(8)

(9)
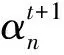
由式(6)得到的能量泛函为

(10)
其中:Fi为第i个波段的融合图像;P为全色图像.
1.3 光谱信息保持约束
假设低空间分辨率的多光谱图像是由高空间分辨率的多光谱图像经过模糊和下采样处理后得到的[8], 每个波段的模糊核存在一定的差异, 需要分波段进行估计, 以保持光谱信息.
本研究采用Krishnan[13]提出的算法进行模糊核的估计, 即

(11)
其中:ki为第i个波段的模糊核, 1≤i≤m;λ和φ控制着对应项的权重大小; *表示卷积运算.


表1 模糊核估计
在此假设下, 得到的能量泛函为

(12)
其中:Ds为下采样矩阵.
1.4 波段比例关系保持约束
多光谱图像波段之间具有一定的比例关系, 融合前后图像波段比例关系保持恒定, 能减轻图像的光谱失真程度.
采用波段比例关系保持约束来表征这种恒定的比例关系[14], 即

(13)
由式(13)得到的能量泛函为

(14)
2 算法框架
算法框架如图1所示.

图1 算法框架Fig.1 Framework of the proposed method
2.1 总能量泛函
综合4个能量泛函, 本研究使用总能量泛函对图像进行融合, 即
其中:γ,λ,μ,η≥0为正则化系数,γ和λ可调节空间信息约束的程度,μ和η可调节光谱信息约束的程度.
2.2 求解过程
为了使总能量泛函最小, 需要依次解决以下3个问题.
① 总能量泛函离散化. 数字图像相当于一个矩阵, 数字图像的数据是离散数据, 设全色图像P、 上采样的多光谱图像M和融合图像F的分辨率为S×T, 定义一个S×T的矩阵H, 则矩阵上的每个点表示图像上的一个像素x∈H.式(15)总能量泛函的离散形式为

(16)
② 总能量泛函极小化. 总能量泛函E(F)对应每个波段Fi的欧拉-拉格朗日方程为

(17)
总能量泛函的极小化与相应的欧拉-拉格朗日方程是等价的, 因此, 总能量泛函E(F)对应的每个波段Fi(1≤i≤m)的欧拉-拉格朗日方程为

③ 求解融合图像F. 通过梯度下降法求解式(18), 使得
则有
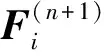

表2 空间和光谱信息保持的多光谱图像融合算法
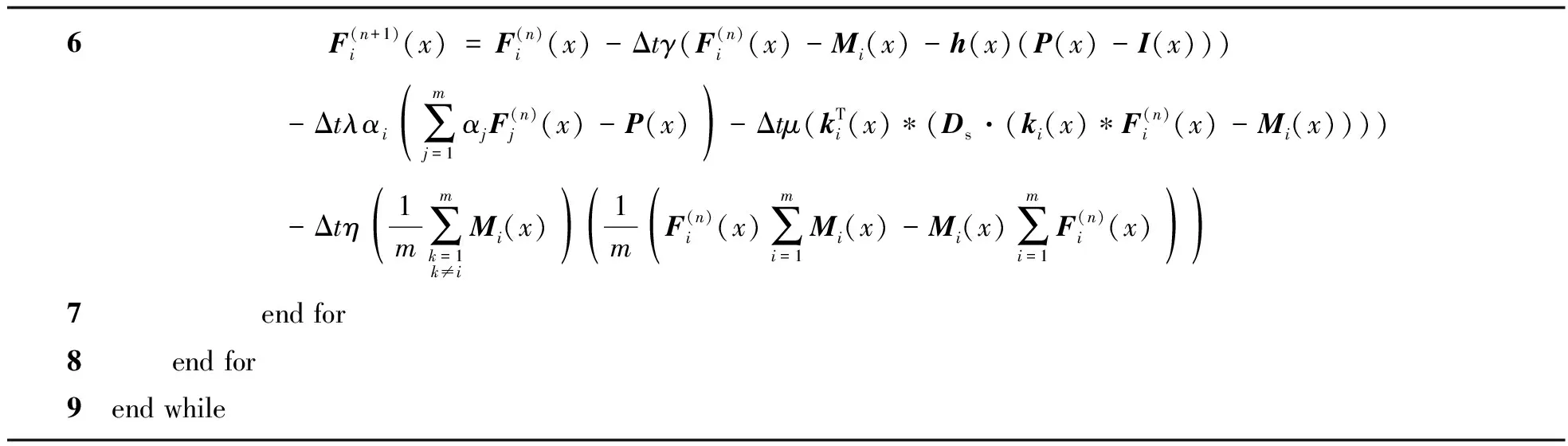
续表2
3 实验结果与分析
使用QuickBird和Pavia University的图像数据验证本文算法, 将本文算法与SFIM[15]、 MTF_GLP[16]、 MTF_GLP_HPM[17]、 PCA[2]、 GS[3]、 GSA[18]、 AIHS[4]和GFPCA[19]等多光谱图像融合算法进行比较, 并从定性和定量两个方面对各算法进行综合分析, 如图2、 3所示.

(a) 参考图像 (b) 全色图像 (c) 经过插值处理的多光谱图像

(d) SFIM (e) MTF_GLP (f) MTF_GLP_HPM

(g) PCA (h) GS (i) GSA

(j) AIHS (k) GFPCA (l) 本文方法图2 QuickBird融合结果Fig.2 Fusion results of QuickBird
分别将QuickBird和Pavia University中的多光谱图像作为参考图像, 大小为256 px×256 px, 如图2(a)和图3(a)所示; 对QuickBird和Pavia University中的多光谱图像进行光谱退化处理, 即对多光谱图像中具有相同坐标位置的像素值求平均, 从而得到全色图像, 大小为256 px×256 px, 如图2(b)和图3(b)所示; 对QuickBird和Pavia University中的多光谱图像分别进行模糊和下采样处理, 得到低空间分辨率的多光谱图像, 大小为64 px×64 px, 将低空间分辨率的多光谱图像插值放大至全色图像大小, 大小为256 px×256 px, 如图2(c)和图3(c)所示. 本节利用得到的全色图像和低空间分辨率的多光谱图像进行融合, 将融合图像与参考图像进行对比. 经实验验证, 当γ=1、λ=0.5、μ=2.5、η=100、 Δt=10-8、ε′=5×10-3时, 融合图像的空间分辨率可以得到提升、 光谱失真问题可以得到有效的减轻.

(a) 参考图像 (b) 全色图像 (c) 经过插值处理的多光谱图像

(d) SFIM (e) MTF_GLP (f) MTF_GLP_HPM

(g) PCA (h) GS (i) GSA

(j) AIHS (k) GFPCA (l) 本文方法
3.1 主观定性评价
图2(d)~(l)和图3(d)~(l)分别表示SFIM、 MTF_ GLP、 MTF_ GLP_ HPM、 PCA、 GS、 GSA、 AIHS、 GFPCA及本文方法在QuickBird和Pavia University图像数据中的融合结果. 如图2(d)、 (f)所示, SFIM和MTF_ GLP_ HPM融合图像的池塘区域会引入一些原图中不存在的信息; 如图2(e)所示, MTF_GLP融合图像的池塘区域颜色发生轻微变化, 光谱信息略微失真; 如图2(g)、 (h)所示, PCA和GS融合图像的颜色和亮度发生了较大的改变, 这意味着PCA和GS的融合结果光谱失真严重; 如图2(i)、 (j)所示, GSA和AIHS虽然引入了自适应的概念, 光谱失真的程度有所缓解, 但GSA的融合结果产生了重影现象, AIHS的融合结果中融合图像的池塘区域颜色发生了明显的改变; 如图2(k)所示, GFPCA的融合结果模糊程度严重, 空间分辨率极低; 如图2(l)所示, 本文方法的融合结果在空间信息和光谱信息上与参考图像相近, 产生了较好的融合效果. 如图3(d)所示, SFIM融合图像的亮度发生了变化; 如图3(g)所示, PCA的融合结果变模糊; 如图3(h)所示, GS的融合结果轻微模糊; 如图3(k)所示, GFPCA的融合结果模糊程度严重, 空间分辨率极低; 如图3(e)、 (f)、 (i)、 (j)、 (l)所示, 对比MTF_GLP、 MTF_GLP_HPM、 GSA、 AIHS和本文方法的融合结果, 本文方法的融合图像颜色与参考图像更为接近, 这说明本文方法对光谱信息保存得更好, 同时, 本文方法的融合图像与图3(c)相比, 空间分辨率有了较大的提升.
3.2 客观定量评价
为了对融合图像的质量进行客观评价, 采用如下4个客观评价指标来评价融合图像的空间和光谱质量.
1) 相关系数(correlation coefficients, CC), 它表示图像几何失真的程度, 即

(21)


(22)
CC的值越接近于1, 融合图像的几何失真程度越小.
2) 光谱角映射(spectral angle mapper, SAM), 它表示图像光谱失真的程度, 即
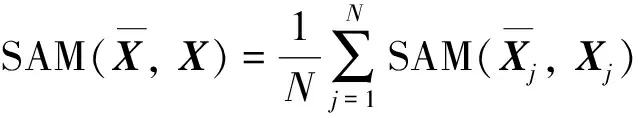
(23)

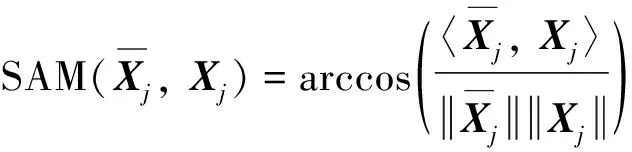
(24)

3) 均方根误差(root mean squared error, RMSE), 它表示参考图像与融合图像对应像素之间的误差, 即
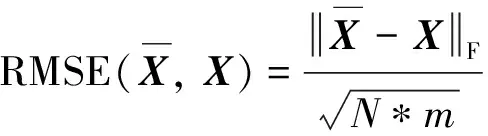
(25)
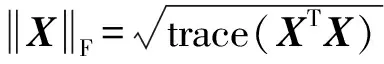
4) 全局相对光谱损失(relative dimensionless global error in synthesis, ERGAS), 它表示融合图像光谱失真程度, 即

(26)

以上4个指标的理想最优值分别写在对应指标后的括号中, QuickBird和Pavia University融合结果的客观定量对比如表3、 4所示.

表3 QuickBird融合结果

表4 Pavia University融合结果
表3、 4中最优结果用黑体表示, 次优结果加下划线. 从表中可以看出, 本文方法在QuickBird图像数据中各项评价指标均是最优值, 在Pavia University图像数据中SAM指标处于次优的位置, 但其他指标均是最优值, 这表明本文方法能在尽量减少光谱扭曲程度的前提下, 使融合图像的空间分辨率得到提升.
4 结语
本研究提出4个约束项, 即边缘自适应提取约束项、 线性组合系数约束项、 光谱信息保持约束项和波段比例关系保持约束项, 联立4个约束项, 建立总能量泛函并求解最优值, 以改善融合图像的空间和光谱质量. 相比其他方法, 本文方法的融合图像视觉效果更为清晰. 综上所述, 本文方法能在尽量保持多光谱图像光谱信息的前提下, 提升融合图像的空间质量, 总体融合质量优于其他方法. 下一步工作将侧重于正则化系数的自适应选择, 以改善多光谱图像融合的质量.

