薄壁空心墩有效刚度试验研究
邵长江,韦 旺,孙南昌,漆启明,胡晨旭,佐 雪
(1.西南交通大学 土木工程学院,四川 成都 610031;2.陆地交通地质灾害防治技术国家工程实验室,四川 成都 610031)
有效刚度是分析桥墩动力特性的关键物理量,同时有效刚度的使用也为建立非线性桥墩的双折线简化分析模型奠定了基础[1-2]。通常取屈服点对应的刚度作为桥墩有效刚度,故计算桥墩有效刚度的关键是屈服点的确定。众多学者、规范根据能量等值原则或Park法等定义桥墩有效刚度。Mehanny等[3]认为随着轴压比的增大,有效刚度最大值可以取到0.9倍的初始刚度。Paulay等[4]则认为,轴压比大于0.5时,混凝土墩有效刚度最大值取为0.8倍的初始刚度;轴压比小于-0.05时,取为0.4倍的初始刚度,轴压比在-0.05~0.5之间采用线性插值法取值。基于120个墩柱的试验结果,文献[5]给出轴压比小于0.2时,有效刚度最小值取为0.2倍的初始刚度。Panagiotakos等[6]基于1 000个拟静力试验结果,认为有效刚度均值为毛截面刚度的0.2倍。仅考虑轴压比影响的公式其形式简单、便于工程应用等,得到文献[7-9]的认可。除轴压比外,文献[10-12]研究得出剪跨比对桥墩有效刚度的影响不容忽视,并发展了同时考虑轴压比和剪跨比影响的有效刚度模型。
文献[13-19]认为有效刚度会受到多重因素的同时影响,进而提出了考虑多重因素的计算模型。文献[2]根据能量相等原理,通过把实际弯矩-曲率曲线等效为理想弹塑性弯矩-曲率曲线,来确定墩柱截面的等效屈服弯矩My和等效屈服曲率φy,并定义有效刚度为等效屈服弯矩与等效屈服曲率之比。该模型能同时反映桥墩开裂及钢筋首次屈服时的工作状态,已被诸多规范采纳[20-22]。Kumar等[13]认为轴压比、纵筋率、剪跨比及混凝土抗压强度为其主要影响参数。文献[14-18]在综合考虑多重因素的基础上,给出了不同形式的有效刚度计算公式。文献[14-16]等认为纵筋率对桥墩有效刚度也有较大影响。Berry等[14]给出考虑轴压比、剪跨比及纵筋率等影响的桥墩有效刚度计算模型。Khuntia等[15]则给出考虑纵筋率、轴力偏心距及轴压比等影响的计算模型。Elwood等[17]认为墩顶位移能力受到弯曲、剪切及纵筋滑移位移等多种因素影响,提出了考虑轴压比、剪跨比及纵筋直径等的有效刚度计算模型。受文献[17]影响,文献[11,16,18]从弯曲、剪切和纵筋滑移变形等三方面出发分析有效刚度的主要影响参数,认为除轴压比和剪跨比影响外,滑移变形也是有效刚度的主要控制因素,并通过引入参数来考虑纵筋滑移变形对有效刚度的影响。
基于理论及试验对桥墩有效刚度展开了大量研究,取得的诸多成果已经纳入有关设计规范,并应用于工程实际。然而对于铁路桥墩,我国现行GB 50111—2009《铁路工程抗震设计规范》[23]则取钢筋首次屈服时作为桥墩的屈服点,钢筋首次屈服对应的桥墩有效刚度则少有研究。另外,相比相同外部尺寸的实心墩,铁路薄壁空心墩具有节省材料、减小恒载及一定程度上降低地震惯性力等优点,因而广泛应用于山区高墩大跨桥梁中。空心墩和实心墩的构造、配筋方式(纵筋、箍筋、拉筋)有明显不同,两者约束混凝土效应差异显著,致使墩身裂缝开裂行为和损伤模式不同,因而相同外部尺寸的薄壁空心墩与实心墩刚度差异较大[24-25]。基于实心墩得出的既有成果对空心墩的适用性值得质疑。为此有必要在深入研究有效刚度影响因素的基础上,结合理论和试验成果,系统梳理现有计算公式,为铁路薄壁空心墩寻求最佳的有效刚度计算模型。论文选取轴压比、配箍率为设计变量,通过5个大比尺模型拟静力试验,研究铁路薄壁空心墩有效刚度,对比既有文献成果,分析现有公式估算薄壁空心墩有效刚度的有效性及合理性。
1 既有研究成果
已有研究表明,墩顶屈服位移主要由沿墩身的弯曲、剪切变形及固端纵筋滑移(称为位移三分量)的耦合效应引起[13,19],而影响位移三分量贡献的因素有:轴向荷载、混凝土弹性模量、有效截面面积、墩高、纵筋屈服强度、纵筋直径、配筋率、配箍率、约束混凝土效应等。因此,基于屈服点的有效刚度影响因素相当复杂,既有研究成果给出形式多样计算公式,根据影响因素的依次增多,将既有模型分为以下三类,见表1~表3。表中,μ为轴压比;λ为剪跨比;My为等效屈服弯矩;φy为等效屈服曲率;L为构件有效高度;D为构件截面宽度;db为纵筋直径;ρl为纵向配筋率;fc′为混凝土抗压强度;fy为钢筋屈服强度;e为轴力偏心距。

表1 仅考虑轴压比影响的计算模型
2 试验研究
为寻求圆端薄壁空心墩的有效刚度估算公式,论文选取轴压比和配箍率作为控制变量,设计5个大比尺圆端型薄壁空心墩,进行拟静力加载试验。根据试验现象和试验结果,对比分析设计参数对圆端薄壁空心墩有效刚度的影响,结合有效刚度实测值和各有效刚度公式的计算值,探讨既有计算公式对圆端薄壁空心墩的适用性。
2.1 模型设计
变截面圆端薄壁空心墩试件采用C35混凝土,纵筋均为HRB400φ12,箍筋及拉筋为R235φ6。模型设计参数见表4,各构件的剪跨比统一为6.23,薄弱位置为2-2截面(计算剪跨比的位置)。模型尺寸及配筋见图1,加载制度见图2。
表4 模型设计参数

图1 模型尺寸及配筋(单位:mm)

图2 加载制度
2.2 试验结果分析
根据试验结果,5个试验墩均发生弯曲破坏,墩身微裂纹较密,贯穿裂缝较分散。极限状态下,变截面处混凝土裂缝较宽,受压区混凝土压溃现象显著;角隅处受拉区纵筋拉拔现象不明显。
加载试验过程中,在距墩底大约10 cm处出现第一条微裂缝,随着荷载的继续增加主裂缝相续出现;相邻裂缝之间混凝土的拉应力不超过抗拉强度时,不再产生新裂缝,而原有裂缝斜向继续延伸。外荷载水平较高时,变截面倒角附近受拉钢筋达到屈服强度、受压区混凝土压溃脱落。屈服钢筋的应力增幅小于变形增加的速度,最终导致桥墩最宽裂缝处纵筋拉断[6,25]。上述试验过程中,纵筋首次屈服是由弯曲引起,此时剪切变形及纵向钢筋滑移效应并不显著,故墩顶位移为弯曲变形所致。
确定屈服点是有效刚度定量的关键,通常采用能量等值法和Park法等来确定构件的屈服点。能量等值法是根据P-M-φ曲线通过面积(能量)等效的原则,将M-φ曲线等效为双折线,得到屈服弯矩及屈服曲率见图3。Park法基于力-位移曲线确定屈服点见图4。此外,钢筋首次屈服是判断桥墩是否进入塑性变形的关键点,故GB 50111—2009《铁路工程抗震设计规范》采用截面最外侧钢筋首次屈服时作为桥墩的屈服点,根据钢筋首次屈服确定的薄壁空心墩有效刚度约为等效屈服点确定的1.40倍,见表5。

图3 能量等效法
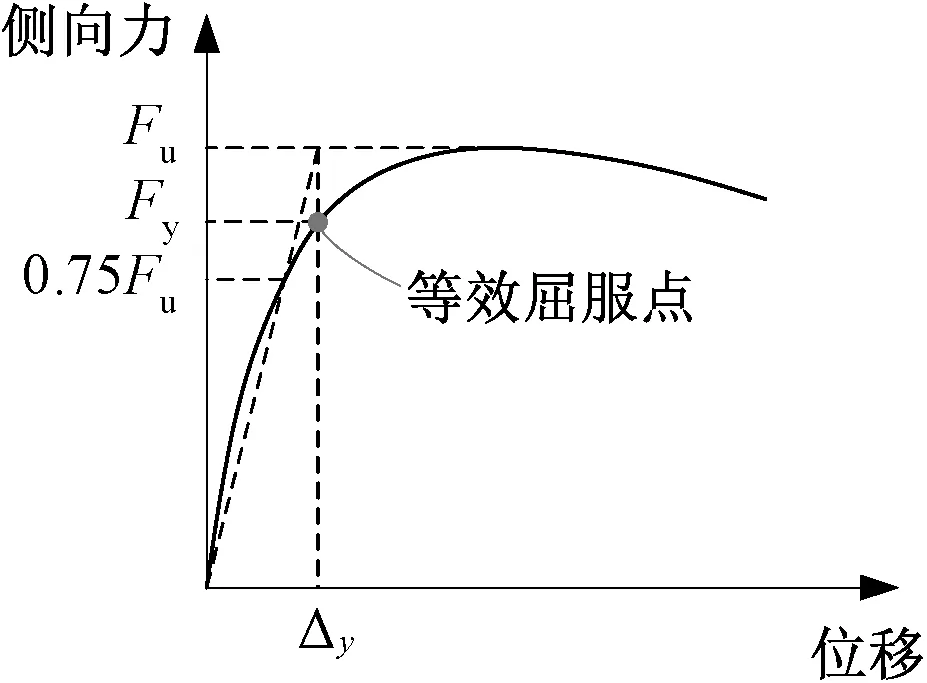
图4 Park法

表5 有效刚度试验结果
针对铁路空心墩,以GB 50111—2009《铁路工程抗振设计规范》指定截面最外侧钢筋首次屈服对应的割线刚度作为桥墩的有效刚度,图1中2-2截面刚度为初始刚度,截面刚度实测结果与截面初始刚度之比见表5。有效刚度比受轴压比及配箍率的影响规律见图5、图6。结合试验结果及综合分析,以文献[18]中试验统计分析得到的桥墩有效刚度模型为基础,得到圆端薄壁空心墩有效刚度计算公式为

图5 轴压比对有效刚度实测值的影响
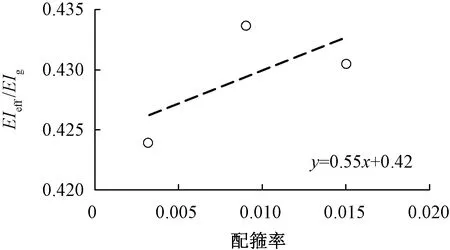
图6 箍筋率对有效刚度实测值的影响
(1)
由图5、图6可知,圆端薄壁空心墩有效刚度受轴压比的影响较显著,且随轴压比的增大而增大。虽然箍筋对混凝土的约束效应起到增强截面刚度的作用,但是对于薄壁空心墩来说约束效应相对较弱,因此箍筋对薄壁空心墩有效刚度的影响不是很大。
3 现有公式对比分析
为方便比较现有公式的适用性,试件有效刚度的计算值与实测值之比见表6。S-B2试验实测轴压比为0.137,有效刚度根据实测值计算。各公式计算值比较见图7,两类结果的比值见图8。

表6 有效刚度公式计算值与试验值之比
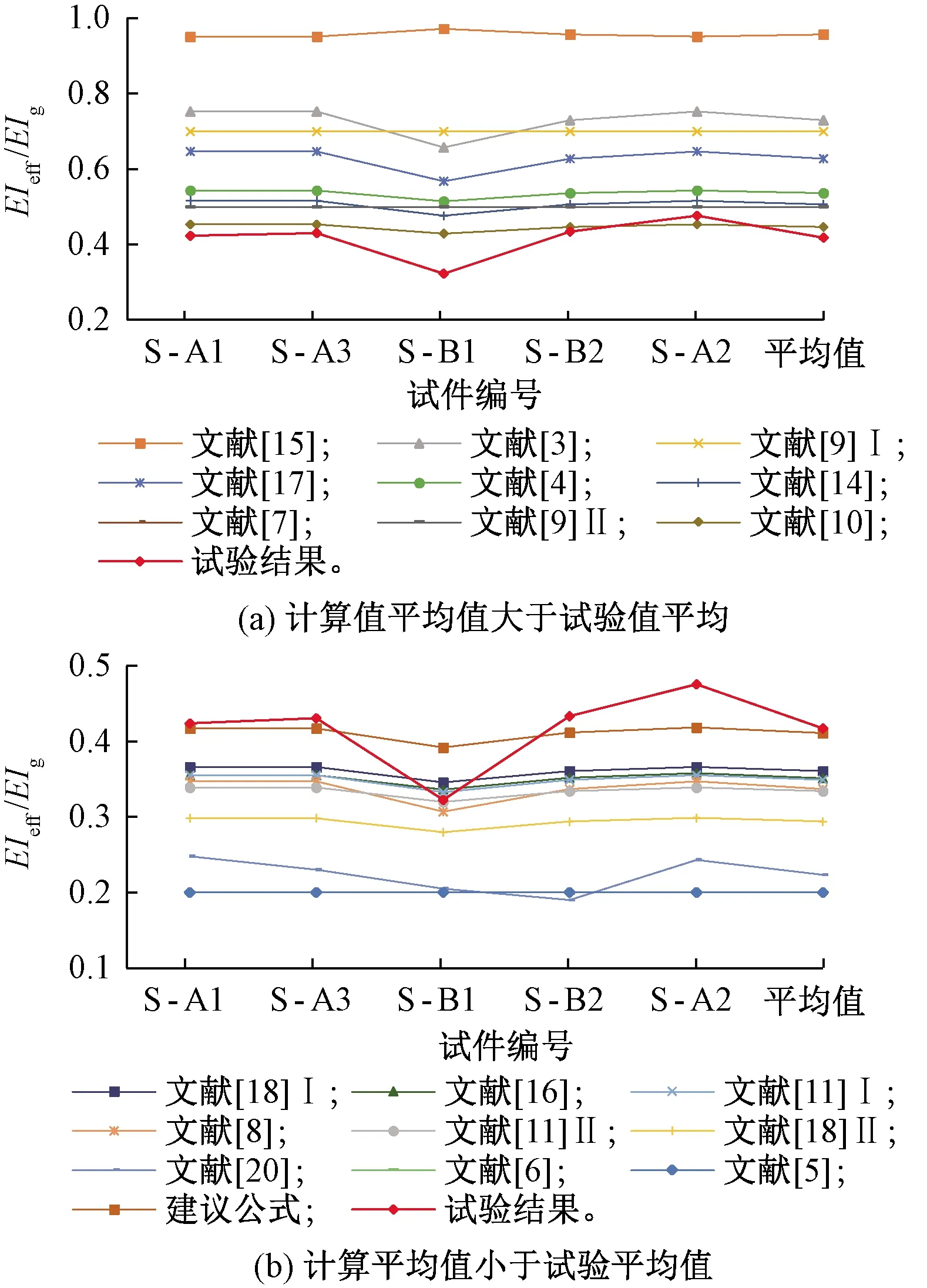
图7 有效刚度计算值与试验值比较
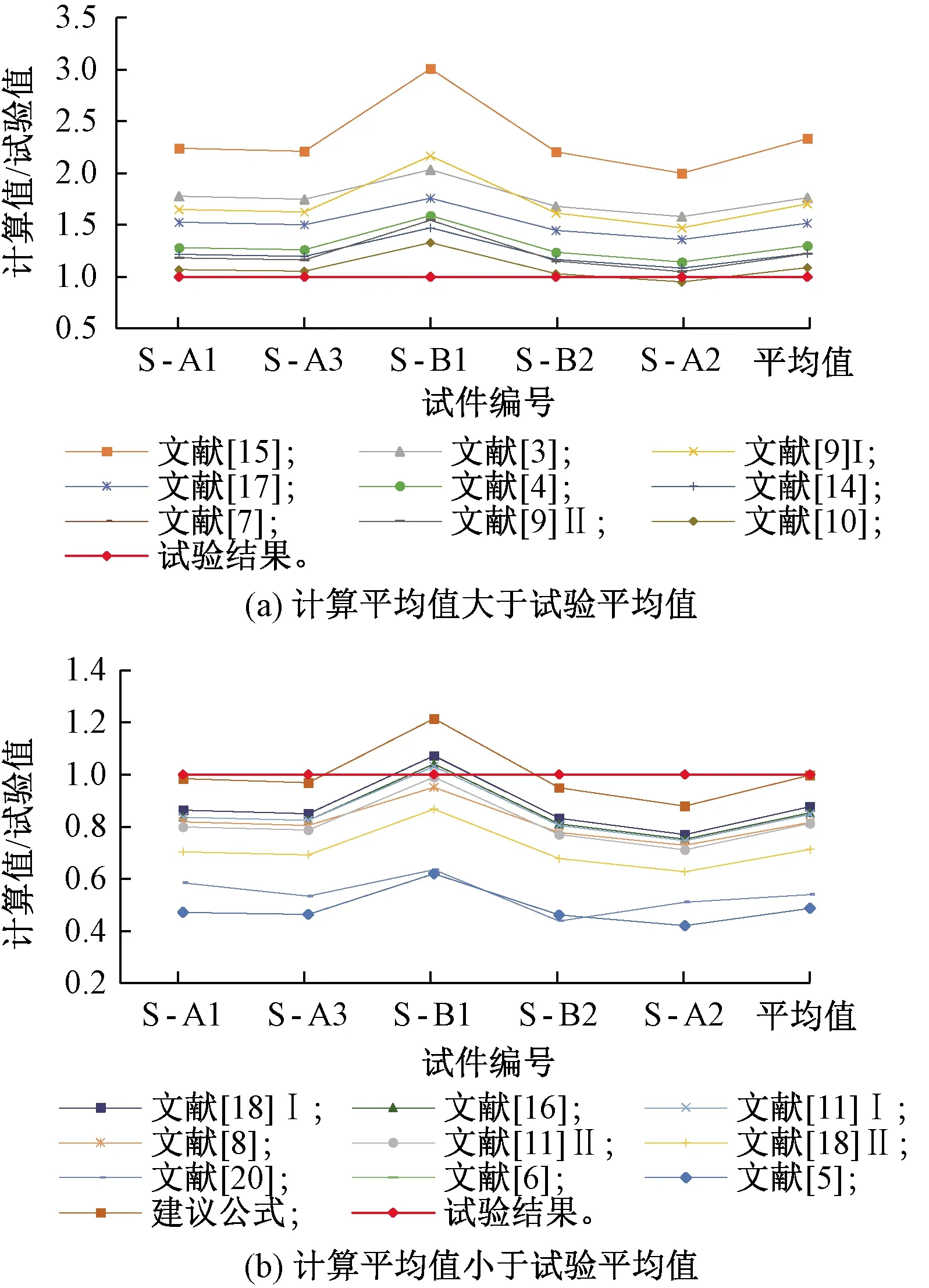
图8 有效刚度公式计算值/试验值
由表6及图7、图8中圆端空心墩有效刚度估计结果对比分析可知:
(1)设计参数影响规律:由图7可知,S-B1试验结果与各公式计算值变化差异较大,但总体上呈现一定规律。由S-B1、S-B2、S-A2的试验结果可知,除文献[15]给出相反规律,文献[5-6,9]有效刚度为定值外,其余公式的计算值与试验值变化规律基本一致,都是随轴压比的增大而增大。由S-A1、S-B2、S-A3的试验结果可知,当轴压比不变而配箍率变化时,试验值一定程度上随配箍率的增大而增大,而各计算结果几乎为定值,并未考虑配箍率的影响,这与论文结果有较大差异。同时,与配箍率比较小的S-A1相比、S-B2的试验值反而比S-A1试验值大,原因在于S-B2试件混凝土抗压强度大于S-A1试验混凝土抗压强度,有效刚度随混凝土抗压强度的增大而增大的趋势。但现有模型中均未单独考虑混凝土抗压强度的影响。
(2)公式合理性:由表6和图8可知,分析有效刚度计算值与试验值之比,文献[5-6,20]、文献[18]Ⅱ等较大地低估了圆端薄壁空心墩的有效刚度,而文献[8,11,16]、文献[18]Ⅰ等的计算值则较为保守,其余现有公式对圆端型薄壁空心墩有效刚度的估计普遍偏高。除文献[10]外,模型[3-4,7,9,14-15,17]较大程度上高估了圆端薄壁空心墩的有效刚度,计算值均超过试验值的1.218倍,容易导致不安全的设计结果。相对于低估了圆端薄壁空心墩的有效刚度的结果相比[5-6],文献[20]的估计值较为接近试验值,三者平均比值分别为0.487、0.487和0.540,总体上这种过于保守的估计值会造成实际工程上的浪费等。模型[8,10-11,16,18]及本文公式的计算值与试验值相对较为接近,平均比值在0.714~1.086之间。
(3)公式适用性:根据表6的结果,尽管文献[16]的计算结果与试验实测值比较接近,但是没有考虑到剪跨比的影响,研究表明有效刚度受剪跨比的影响较为显著,对于不同剪跨比的试件,该公式是否适用还有待验证;文献[8]计算值与试验值也较为吻合,但其仅考虑轴压比的影响,这种简单处理方式,导致其适用性有限;文献[11]的计算值较接近于试验值,而与其公式Ⅱ相比,考虑了轴压比及剪跨比影响的公式Ⅰ计算效果更好,但相对于公式Ⅰ,文献[10,18]及本文公式的计算值更接近于试验结果(见图8)。
综上所述,文献[10,18]对于圆端型薄壁空心墩有效刚度的估计效果相对较好,而前者计算值略大于试验值,会造成不安全的设计结果。而建议公式更适用于估算圆端型薄壁空心墩的有效刚度,偏于保守的估计则可采用文献[18]的公式Ⅰ。
4 结论
通过分析国内外相关研究成果,系统梳理了现有桥墩有效刚度计算公式,并基于拟静力试验结果,探讨了圆端型薄壁空心墩有效刚度的影响因素,研究了现有桥墩有效刚度计算公式的适用性。结果表明:
(1)试验构件均发生弯曲破坏,墩底变截面处损伤严重,主干裂缝遍布墩身,侧向斜裂缝明显,构件延性性能较好。
(2)与常规桥墩相比,圆端型薄壁空心墩有效刚度的影响因素大体相同,但受各因素(轴压比、剪跨比、纵向配筋率、纵筋直径、纵筋屈服强度、配箍率及混凝土强度等)影响的显著性有所差异。
(3)文献[3-4,7,9,14-15,17]的计算结果过于偏高,容易导致不安全的设计结果,文献[5-6,20]的计算结果过于保守,不太适用于估算圆端型薄壁空心墩有效刚度。
(4)文献[8,15]的计算效果较好,但其考虑因素过于单一,不大适用于估算圆端型薄壁空心墩的有效刚度。文献[11]的相对误差大于15%,也不大适用于计算薄壁空心墩的有效刚度。
(5)文献[10]、文献[18]Ⅰ对于圆端型薄壁空心墩有效刚度的估计效果相对较好,文献[10]的计算值略大于试验值,容易导致不安全的设计结果。偏保守考虑,则可采用文献[18]中的公式Ⅰ。
综合分析,所建议公式更适用于估算铁路薄壁空心墩的有效刚度。限于模型试验设计参数及试件加工数量,现有研究尚无法全面揭示各类因素对圆端型薄壁空心墩有效刚度的影响及规律。针对圆端型薄壁空心墩有效刚度的计算公式,仍需更多、更深入的针对性试验研究。

