优化的灰色马尔科夫模型在油气集输管道腐蚀预测中的应用
李昊燃,郑度奎,程远鹏,何天隆,唐善法
(长江大学 石油工程学院,武汉 430100)
随着油气集输管道在役时间的延长,多数管道出现腐蚀现象。油气集输管道腐蚀直接关系到管道的使用寿命、经济效益以及环境安全[1-2]。因此,科学、准确地预测油气集输管道的腐蚀速率,对延长管道的使用年限、减少经济损失、保障环境安全具有重要的意义。
油气管道的腐蚀预测有多种方法,其中灰色模型(GM)是应用比较多的一种方法[3-7]。但是灰色模型并没有考虑各个因素间的关系,只是对数据间的变化规律进行了分析,对数据依赖性较强,预测结果会随着数据的波动而产生较大的误差。为了追求更为精确的预测结果,许多学者对灰色预测模型进行了改进。龙学渊等[8]在原有灰色预测模型基础上建立了不等时距灰色预测模型,扩大了等时距灰色模型的使用范围,且取得了比较准确的预测结果。李秀娟等[9]通过灰色预测模型和BP神经网络模型相结合的方式对原有模型进行改进,较大程度上提升了预测精度和计算速度。经建芳等[10]建立了灰色线性回归组合模型,新模型即考虑到了原始数据的线性因素,又考虑了其他非线性因素,最终得到了较好的预测结果。
然而仅利用灰色模型来进行预测,预测结果会受到原始数据的影响,从而产生较大的误差。为了在油气管道腐蚀预测中获得更加可靠的数据,需要对预测结果进行误差修正,使其具有更高的预测精度。马尔科夫模型适用于随机过程的状态转移行为,且需要修正的样本数据具有平稳过程、等均值的特点。灰色模型预测结果产生的误差比较适合使用马尔科夫模型来进行修正。因此,本工作先从无偏模型、背景值、数据更新等方面对原有的灰色预测模型进行改进,而后引入马尔科夫模型对预测出的数据进行误差修正,有效减小了由原始数据的波动而产生的误差。
1 灰色马尔科夫预测模型
1.1 GM(1,1)预测模型
1.1.1 GM(1,1)预测模型建立


(1)
由算子序列X(1)求出GM(1,1)模型背景值Z(1)={z(1)(1),z(1)(2),z(1)(3),z(1)(n)}。其中,z(1)(k)=0.5[x(1)(k)+x(1)(k-1)],(k=2,3,4,…n)。根据所得的背景值,对GM(1,1)模型的白化方程离散化,使其由微分转变成差分,从而得到GM(1,1)模型的灰微分方程,如式(2)所示。
X(0)(k)+aZ(1)(k)=u
(2)
根据式(2)建立矩阵,通过最小二乘法原理求得发展系数a和灰色作用量u,如式(3)所示。

(3)
则算子序列X(1)的预测公式为
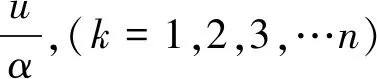
(4)
将上式进行累减还原就可以得到预测值为
(1-eα)e-αk,(k=1,2,3,…n)
(5)
1.1.2 模型检验
为了确认模型预测结果的可靠程度,需要对预测模型的精度和可信度进行检验。一般使用残差检验和后验差检验[11]。
残差检验是逐点检验,即k时刻的残差为
ε(0)(k)=X(0)(k)-X′(0)(k),(k=1,2,3,…n)
(6)
式中:X(0)(k)是样本数据值,X′(0)(k)是预测值。
残差均值:

(7)
残差方差:

(8)
原始数据均值:

(9)
原始数据方差:
(10)
后检验差检验指标为后验差比值C和小误差概率P,分别如式(11)和(12)所示。
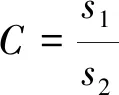
(11)
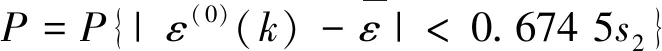
(12)
根据P、C值参照精度检验表(见表1)可对已建模的精度做出评估。

表1 精度检验表Tab. 1 Accuracy inspectionTable
1.2 马尔科夫预测模型
油气管道腐蚀速率的实测值和使用灰色预测模型预测出的预测值之间存在较大的误差,故使用马尔科夫链对预测结果中产生的波动性误差进行修正[12]。对灰色预测模拟产生的误差进行区间状态划分,把区间划分为E1,E2,…,En,依据马尔科夫的无后效性,i(1≤i≤n)时刻的状态只与i-1时刻的状态有关系,不受之前状态的影响。从状态Si经过一步转变成状态Sj的概率为Pij,通常用n阶方阵P来表示一步转移概率矩阵,如式(13)所示。
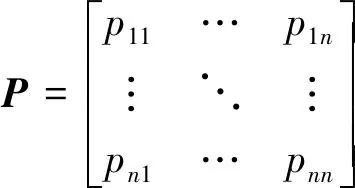
(13)
则从状态S经过一步转移后的状态S0可表示为S0=S×P,预测出状态后,其腐蚀速率计算式[13]为

(14)
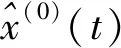
2 优化的灰色马尔可夫预测模型
2.1 无偏灰色预测模型
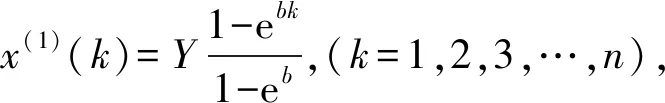
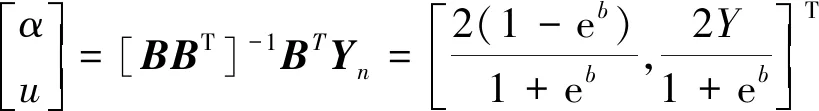
(15)
得到

(16)
无偏GM(1,1)模型的预测值为

(17)
相比于传统的GM(1,1)预测模型,无偏GM(1,1)模型消除了传统模型中的灰色偏差,即使在数据增长较大的情况下也可以进行有效可靠的预测,同时无偏GM(1,1)模型是以原始数据为基础构建的模型,不需要对得到的数据再进行累减还原,从而简化了整个计算的过程。
2.2 灰色预测模型背景值的优化
由传统的GM(1,1)预测模型能够看出,发展系数a和灰色作用量u是决定GM(1,1)模型预测精度的关键因素,而a和u的值是由矩阵B决定的,矩阵B由背景值构成。所以GM(1,1)模型的预测精度受到背景值的影响[15]。传统GM(1,1)预测模型的背景值为Z(1)(k)=0.5[x(1)(k)+x(1)(k-1)],(k=2,3,4,…,n),在传统的灰色预测模型中,用每个空间步长所对应梯形的面积来替代积分区域的面积(如图1所示),空间步长越大两者差值越大,进而使得预测结果产生一定的误差。模型背景值优化即使用积分区域的面积作为背景值,可消除背景值产生的误差。

图1 背景值误差分析Fig. 1 Error analysis of background value
2.3 数据更新
为了减小数据波动产生的误差,采用数据实时更新的预测方法[16],即使用原始数据X(0)={x(0)(1),x(0)(2),x(3),…,x(0)(n)}预测出x(0)(n+1),然后在原始数据列X(0)的基础上去掉x(0)(1),以x(0)(2)为起始数据,加入x(0)(n+1)构成新的等长度数据列X(i),使用新构造的数据列来预测x(0)(n+2)。这样每次预测能使用最新数据,可以有效减少由于预测远期问题而产生的动态偏差。
3 实例分析
以某油田特定实验区集输管道腐蚀速率检测数据为例[17],每30 d测量一次数据,在420 d内进行15次测量,其腐蚀速率实测值如表2所示。
使用Matlab软件对预测模型进行编程计算,分别采用传统GM(1,1)模型和改进后GM(1,1)模型以表2中的前12组腐蚀速率实测数据为样本数据进行模拟预测,预测结果列于表3中。计算得改进后模型预测结果的后验差比值C约为0.180 42,小误差概率P为1,对比精度检验表可知,该模型的预测精度等级为好,可以使用该模型进行腐蚀预测[13]。
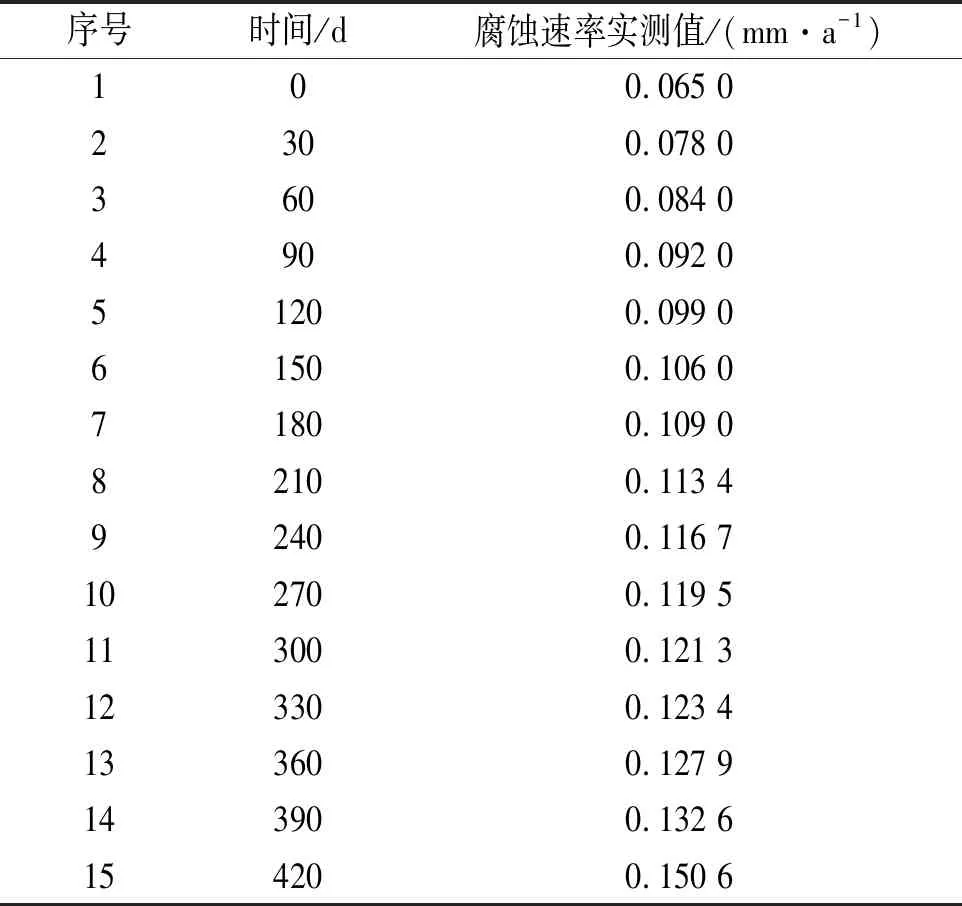
表2 管道腐蚀速率实测值Tab. 2 Measured values of pipeline corrosion rate
从表3可以看出,传统GM(1,1)模型预测结果的平均相对误差为3.601%;而改进后无偏GM(1,1)模型预测结果的平均相对误差为3.166%,相比于改进前,精度提高了12.08%。虽然改进后无偏GM(1,1)模型的预测精度有所提高,但是仍然存在误差较大的预测值。

表3 不同模型预测的管道腐蚀速率及误差分析Tab. 3 Corrosion rates of pipeline predicted by models and error analysis
优化的灰色马尔可夫预测模型是指用马尔科夫模型对改进后无偏GM(1,1)模型的预测结果进行修正,预测管道的腐蚀速率。首先,以预测结果产生的相对误差为划分依据进行状态区间划分;然后,按照划分的结果对相对误差比较大的预测值进行修正,划分结果见表4。

表4 平均误差状态区间划分Tab. 4 Average error state interval division
根据残差状态划分结果计算出状态转移概率矩阵,如式(18)所示。

(18)
通过状态转移概率矩,根据已经预测的数据结果对未来的状态做出较为可靠的预测。根据每组数据所处的状态,对误差较大的(一般误差>1%)预测结果进行修正[18],以第2组数据为例,第2组数据处于状态4,根据式(14)计算得到修正后的预测值为

(19)
最终得到误差修正后的预测结果,如表3所示。
结果表明,引入马尔科夫模型对误差进行修正后,预测结果的平均相对误差减小至0.83%,相对于无偏GM(1,1)模型和传统GM(1,1)模型,其预测精度有较大幅度的提升,分别提高了73.8%和76.95%。
依靠样本数据直接采用不同模型预测腐蚀不同时间后管道的腐蚀速率(表3中最后3组数据),用相应的实测腐蚀速率(表2中最后3组数据)进行验证,结果如表5所示。从表5中可以看到:传统GM(1,1)模型的误差较大,平均相对误差达到了4.67%;而改进后的无偏GM(1,1)模型的误差明显减小,平均相对误差降低至2.41%,与传统GM(1,1)模型比,预测精度提升了48.39%;优化的灰色马尔科夫模型,其平均相对误差只有1.12%,相对于无偏GM(1,1)模型,精确度提高了53.5%,有着较为明显的提高。总的来说,改进后模型比原模型预测精度更高,并且有效改善了传统GM(1,1)模型中长期预测误差较大的缺陷。

表5 验证数据与各模型预测结果的比较Tab. 5 Comparison of verification data and prediction results of different models
图2为不同模型预测的管道腐蚀速率随时间的变化曲线。从图2可以直观地看到,三种预测模型中,灰色马尔科夫模型的预测值最接近实测值。

图2 不同模型预测的管道腐蚀速率随时间的变化曲线Fig. 2 Curves of pipeline corrosion rate predicted by different models with time
4 结论
(1) 改进后的灰色无偏模型相比于传统灰色模型,预测精度有较大提高,有效改善了传统灰色预测模型在中长期预测时精度下降的问题;再引入马尔科夫模型对灰色模型预测出的结果进行误差修正,避免了因为原始数据波动而产生的误差,修正后的模型能够更加精确的预测管道腐蚀速率。
(2) 使用优化的灰色马尔科夫模型能够提供更加可靠的管道腐蚀速率预测数据,有利于掌控管道的腐蚀状态,对管道维修和腐蚀安全防护以及提高经济效益起到至关重要的作用。

