基于振动信号分析的动力调谐陀螺仪滚珠轴承故障诊断∗

蔡文迹李醒飞鲁建宇(天津大学精密测试技术及仪器国家重点实验室,天津300072)

陀螺仪是惯性导航系统的核心元件之一,用于测量载体的角速率[1]。在多种类型陀螺仪中,凭借其优势——双自由度、体积小、精度高、成本低等,动力调谐陀螺仪在很多领域受到了广泛应用[2]。由于长期反复电机启动、振动冲击等会造成动力调谐陀螺仪精度下降或陀螺仪失效,对正在执行任务的惯性导航系统会带来难以弥补的损害[3]。为此开展动力调谐陀螺仪故障诊断,对保障惯性导航系统正常运行具有重要意义。

滚珠轴承作为动力调谐陀螺仪重要的支撑部件,其性能好坏直接影响到陀螺仪的驱动轴乃至整个惯性导航系统的正常运转[4]。国内外研究学者针对轴承以及陀螺仪的故障诊断方法也已做出了许多相应研究。2013年,李醒飞,王佳等人从陀螺仪结构模型入手通过参数辨识实现了对挠性陀螺仪表头的性能分析[5]；2016年,Anastasiya等人通过计算静态气动轴承特性的数学模型评估该轴承在球陀螺仪中的性能[6]；2017年,华显伟基于ADAMS仿真软件建立了惯导轴承动力学仿真模型并实现对惯导轴承的磨损评估[7]；2018年,李岩将稀薄气体润滑理论与陀螺仪漂移误差研究相结合,提出了一种对动压气浮陀螺仪轴承性能分析方法[8]。上述研究均针对陀螺仪故障或者对应轴承性能展开了分析,但目前工程上针对动力调谐陀螺仪滚珠轴承故障的诊断方式研究却较为鲜见,诊断方式往往还是通过测量其同步时间和滑行时间是否超过相应阈值来进行判定。该方式需要对陀螺仪进行启动与制动,故无法对处于工作状态中的陀螺仪进行故障诊断,而且由于陀螺仪内部结构的复杂性,陀螺仪中的其他故障部位同样也会对判断结果造成干扰。因此,为了更加精确且及时地对动力调谐陀螺仪滚珠轴承作出故障诊断,本文基于石英挠性加速度计和LabVIEW软件搭建了振动测试系统,通过对动力调谐陀螺仪滚珠轴承所产生振动信号进行实时采集、处理,并针对振动信号的特征频率进行频域分析和小波分析,实现对动力调谐陀螺仪滚珠轴承的实时故障诊断。

1 滚珠轴承及其振动信号特征频率

如图1所示,滚珠轴承通常是由内、外滚道、保持架和滚珠四个部分组成。其作用是通过内外滚道间滚珠运动时的滚动摩擦来取代了原来面与面之间的滑动摩擦,从而大大降低了由于摩擦阻尼给系统造成的能量损耗,同时也起到连接驱动电机与陀螺转子,使陀螺转子能同步电机转速进行转动的作用。

图1 滚珠轴承的结构示意图

设D、d、r1、r2、α、N分别表示滚珠轴承的轴承节径、滚珠直径、内滚道半径、外滚道半径、接触面夹角和轴承转速(大小即为电机转速),以下是滚珠轴承处于工作状态下可能会产生的一系列特征频率[9]:

①设内滚道转动频率fr,则有:

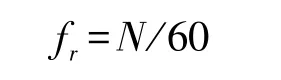
当一个滚珠经过内滚道上某一点时的频率为fi,则有:

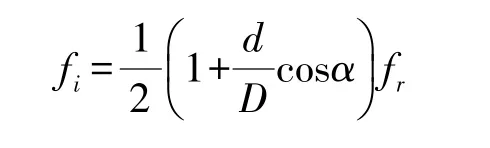
当n个滚珠经过内滚道上某一点时的频率为nfi,则有:

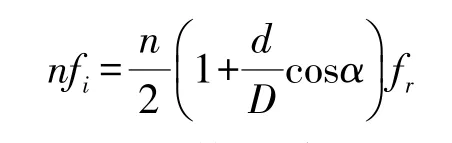
②当一个滚珠经过外滚道上某一点时的频率为fc,则有:

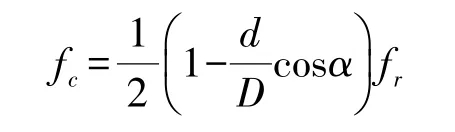
当n个滚珠经过外滚道上某一点时的频率为nfc,则有:

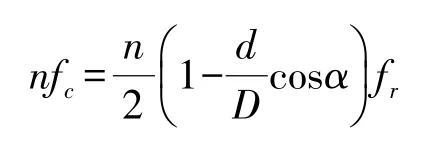
③当滚珠上的某一点经过内滚道或外滚道时频率为fb,则有:

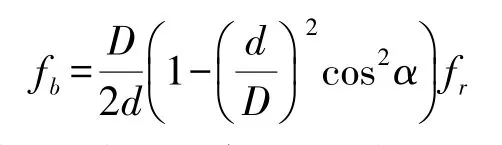
④保持架的转动频率为f,则有:

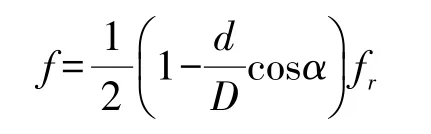
在对滚珠轴承进行振动故障诊断时通常以上面所描述的特征频率的变化作为判断依据。

以下是滚珠轴承产生振动的主要三类原因以及各自所对应的振动特征频率。

①由于滚珠轴承自身的结构缺陷所引起的振动。此类振动主要来源于组成部件受力发生形变、驱动轴弯曲、滚珠间尺寸不一致这三种因素。该振动频率主要包括:fc、nfc±fr(n为自然数)。

②由于滚珠轴承的非线性所引起的振动。此类振动主要是由于在长期工作后,轴承的润滑状态出现下滑而导致。该振动频率主要包括:fr及其倍频2fr,3fr,…,和分频(1/2)fr,(1/3)fr,…。

③由于滚珠轴承磨损或缺陷所引起的振动。此类振动主要来源于轴承磨损、内、外滚道缺陷、滚珠缺陷这四种因素。该振动频率主要包括:nfr、fo及其倍频2fo,3fo,…nfo、fi及其倍频2fi,3fi,…nfi、fb及其倍频2fb、3fb,…nfb、nfo±nfr、nfo±nfc、nfb±nfc。

综合上述几种滚珠轴承产生振动的主要原因和特征频率,结合动力调谐陀螺仪工作中实际测试情况,动力调谐陀螺仪滚珠轴承故障所引发的振动信号特征频率主要表现为陀螺仪驱动电机的转频fN(即fr)及其分频fN/n和倍频nfN。下面设计振动测试实验对该故障所产生的振动信号进行采集和分析。

2 振动测试实验设计及振动信号分析

2.1 振动测试实验设计

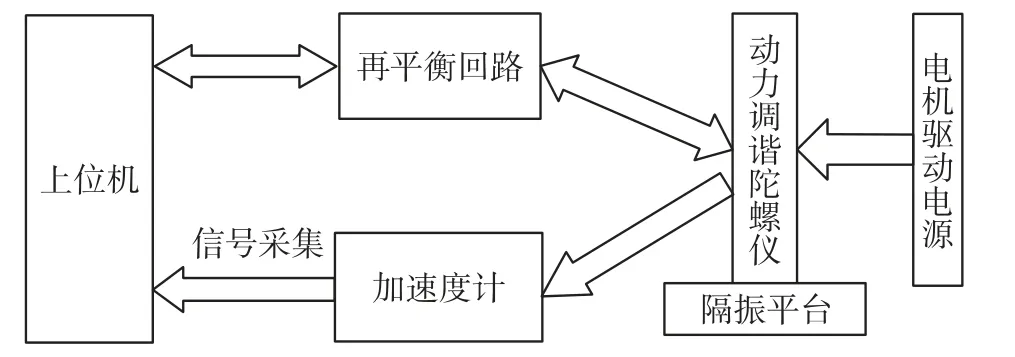
图2 振动测试实验系统结构框图

如图2所示,动力调谐陀螺仪振动检测系统设计大体应包含两大部分:一是动力调谐陀螺仪闭环再平衡回路的搭建。其中主要由待测动力调谐陀螺仪、陀螺仪电机驱动电源、陀螺仪激磁电源、闭环再平衡回路模拟电路、数据采集电路、工控机组成,其中,动力调谐陀螺仪、上位机、闭环再平衡回路通过数据采集电路的连接形成闭环,陀螺仪驱动电源为陀螺仪提供500 Hz、20 V线电压的三相电；二是陀螺仪振动信号采集电路的搭建。其中主要由待测动力调谐陀螺仪、高灵敏度加速度计、安装工装、隔振平台、信号采集电路组成。加速度计选用的是HB309石英挠性加速度计,该加速度计测量频率带宽为0～2200 Hz,最大电压输出值为±11 V,加速度测量范围为0～±70 gn,最小敏感量10－6gn,满足实验要求。安装工装用于固定陀螺仪和加速度计,并使加速度计能够分别安放在陀螺仪径向和轴向,便于测试陀螺仪的径向和轴向振动,安装工装与陀螺仪、加速度计实装图如图3所示。隔振平台屏蔽外界振动可能给实验带来的干扰。振动测试实验系统整体搭建如图4所示。

图3 陀螺仪、加速度计和安装工装实装图

图4 振动测试系统整体实物图

为了便于对实验数据实时采集和分析,在上位机软件LabVIEW中设计采集程序完成对振动信号的采集和处理。在陀螺仪振动测试实验中,加速度计实时反馈回来的电压信号经过采样电路的AD转换后由事先定义好的I/O口输入到上位机的NI PCI-6289采集卡中,然后通过LabVIEW里事先设置好的信号采集程序对采集到的数据进行处理和保存用于后面的分析。

2.2 振动信号分析

完成振动检测系统的软硬件搭建后,开始对某型号的动力调谐陀螺仪进行振动信号采集。该型号陀螺仪的电机转频约为167 Hz,转频二倍频为333 Hz,四倍频为667 Hz,加速度计测量带宽为0～2200 Hz,结合奈奎斯特采样定理[10],采样率设置为8 KS/s。

在进行频域和小波分析前,为了对陀螺仪的滚珠轴承状态作出初步判断,先对四个动力调谐陀螺仪的同步时间和滑行时间进行测试,测试结果统计如表1所示。

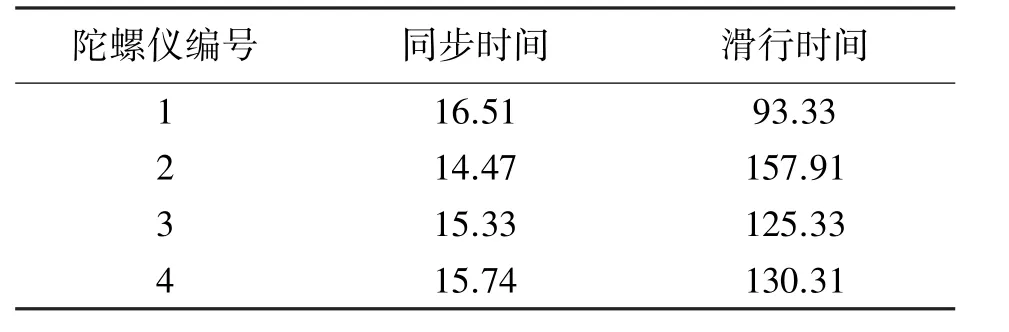
表1 陀螺仪同步时间与滑行时间统计 单位:s

由于该型号陀螺仪出厂要求的同步时间小于20 s、滑行时间大于60 s且小于90s,从同步时间和滑行时间测试结果可以判断,2、3、4号陀螺仪的滚珠轴承出现故障可能性较大,1号陀螺仪正常。

下面分别从频域和时域角度对振动信号展开分析,并作出故障诊断。

2.2.1 频域分析

由于本实验频域分析研究重点是特征频率所对应的能量大小,信号的功率谱密度能够反映信号中各频率成分的能量强弱分布状况[11],所以选择对振动信号的功率谱密度进行分析。

依次对四个动力调谐陀螺仪采集各自在工作状态下垂直于驱动轴径向方向和沿着驱动轴轴向方向的振动信号,然后对相同方向的振动信号对比其功率谱密度。为便于分析对比,以1 w/Hz为归一化基准对纵坐标功率谱密度进行归一化处理,处理完后纵坐标单位为dB。下面分别对驱动轴径向方向和驱动轴轴向方向的振动信号进行频域分析如图5、图6所示。

对四个测试陀螺仪径向和轴向振动信号在特征频率分别对应为fN、2fN、4fN出的幅值作比较分析,结果统计如表2所示。

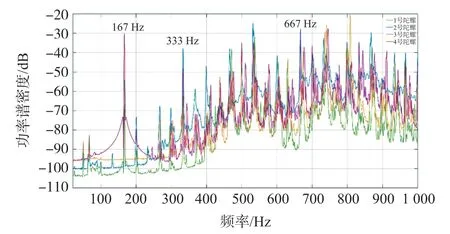
图5 陀螺仪径向振动频域对比图

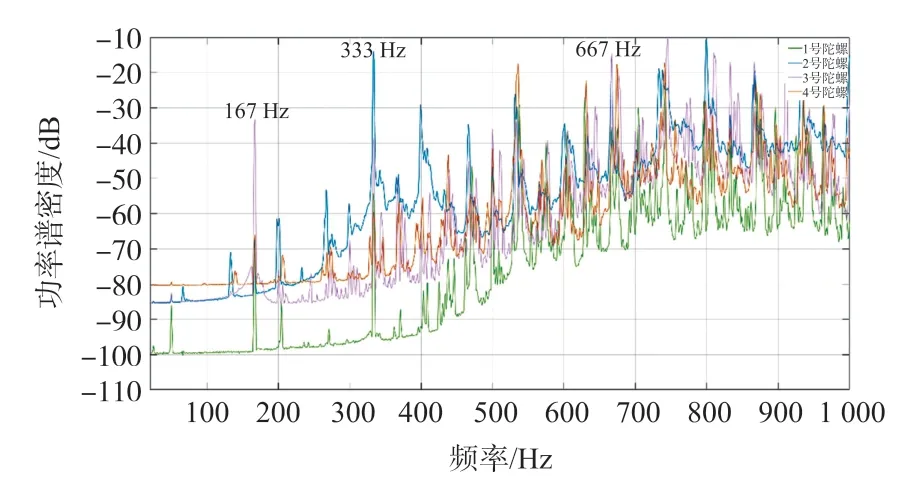
图6 陀螺仪轴向振动频域对比图

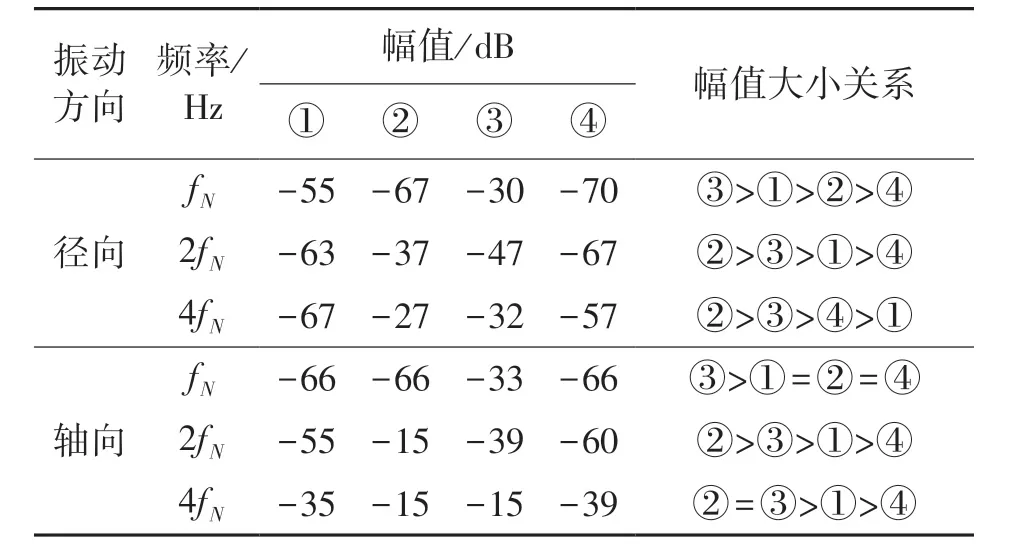
表2 陀螺仪振动信号频谱比较结果统计

由表2中对比结果可以得出:在4fN处,2号和3号陀螺仪对应的幅值都远大于1号和4号陀螺仪,根据滚珠轴承振动特征频率可以预测2号和3号的滚珠轴承出现了故障；比较fN和2fN处的幅值大小可以得到:1号和3号陀螺仪在fN处振动较其他两个陀螺仪更大,2号和3号在2fN处振动较其他两个陀螺仪更大,由于当陀螺仪挠性接头出现故障时在垂直于驱动轴径向方向上也可能产生fN和2fN振动[12],因此判断这两处振动的故障源可能来自滚珠轴承或者挠性接头,综合对比结果可以作出预测:2号和3号陀螺仪滚珠轴承出现故障可能性很大,1、4号陀螺仪存在滚珠轴承故障的可能性,需要作进一步实验分析确认。

2.2.2 小波分析

由于采集得到的原始信号为非线性,运用常用的时域分析方法或者仅通过频域分析的方法,都很难充分获取包含故障信息的振动特征。而作为针对非线性信号的时频分析方法之一的小波分析,能够有效地分析得出包含故障信息的振动时域特征,实现陀螺仪故障部位定位预测。

进行小波分析时需要用到小波变换,其基本思想就是通过小波基函数的伸缩和平移对信号进行多尺度分析[13]。对信号的多尺度分析是通过分层逐次分解进行的,信号每进行一层分解,都会经过一个低通滤波器和一个高通滤波器。其中,经过低通滤波后得到的一系列值称为近似系数,体现信号的大致形状特征,经过高通滤波后得到的值称为细节系数,体现信号的局部细节特征。信号通过低通滤波器后频带会在原有的基础上折半,依据奈奎斯特采样定理,对其进行两倍抽取,将抽取后的信号作为下一层分解的对象。由此可以得出,对于输入信号X[n]作N层小波分解即可以得到一组近似系数cAN和N组细节系数cD1～cDN,N层小波分层逐次分解的流程示意图如图7所示。

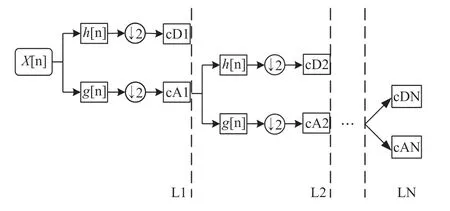
图7 N层小波分解示意图

对测量得到的振动信号进行小波分析具体可分为以下四步:

①分解层数的选定

假设信号X[n]的采样频率为fs,根据奈奎斯特采样定理,X[n]的带宽在fs/2以内。一层小波分解后,细节系数cD1表示的信号带宽为fs/4/4～fs/2/2,近似系数cA1表示的信号带宽为0～fs/4,以此规律作N层分解后,N组细节系数cD1～cDN表示的信号带宽即为fs/2N＋1～fs/2,近似系数cAN信号的带宽在0～fs/2N＋1以内。由此可得小波分解层数N的选择决定了信号分解后的频带范围。为了便于时频分析,以及考虑到振动频率之间的相互影响,进行N层分解之后的近似系数表示的信号带宽上限还应该在陀螺仪电机转频fN和2fN之间,2fN与4fN也应该尽可能处于不同的近似系数与细节系数代表的频段中,这样通过小波分解就能将转频及其倍频在时域上的变化特征分别表现出来。由于已知fN为167 Hz、2fN为333 Hz、4fN为667 Hz,因此分解层数N应该满足的关系式如式(1)所示:

当信号采样率为8 KS/s时,计算得到当N＝4时满足条件。

②小波基函数的选定

在选取小波基函数时,需要根据小波变换应用背景对其特性的要求来选择合适的小波基函数。一般常用的小波有Morlet小波、Haar小波、dbN小波等[14]。其中,Haar小波的形式简单,但不连续,频域上容易造成频谱泄漏；Morlet不具备紧支撑性；而dbN小波具有连续性、紧支撑性与正则性,且具有N阶消失矩,结合振动信号分析要求综合考虑后,选取dbN小波作为本实验小波分解的小波基函数。

③基于小波方差的近似系数与细节系数小波分析

要对比不同陀螺仪在相同频段的时域内幅值变化,就需要对小波近似系数和细节系数进行特征提取,找到一个指标来反映振动幅值强弱的变化。尺度m下的小波方差计算方式如式(2)所示,该特征量可以看作信号序列在单一尺度下的平均能量,因此可以表示振动幅值强弱的变化[15]。

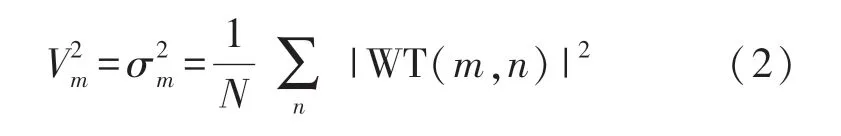
式中:N为尺度m下小波系数的个数,WT(m,n)为随着n的平移计算出来的尺度m下的所有小波系数。

④对于依据电机转频及其倍频选取合适的细节系数与近似系数完成时域比较。

由于经历4层分解后近似系数表示的带宽为0～250 Hz,fN包含在其中,第四层的细节系数表示的带宽为250 Hz～500 Hz,2fN包含在其中,第三层细节系数表示的带宽为500 Hz～1000 Hz,4fN包含在其中。因此,电机转频及其倍频通过四层小波分解分别被不同的频段所表示出来,便于分别进行比较分析,下面对陀螺仪测得的振动信号中此三个频率所对应的近似系数与细节系数的方差进行比较。

下面分别对动力调谐陀螺仪径向和轴向的振动信号进行小波分析如图8、图9所示。

图8 径向振动小波分析比较

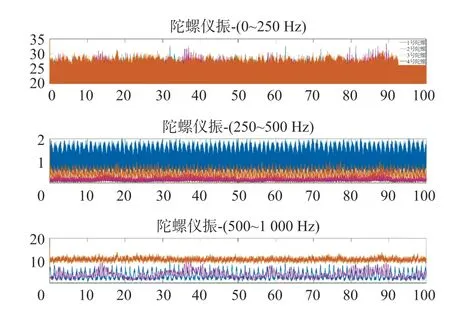
图9 轴向振动小波分析比较

通过上面小波分析可知:1号陀螺仪的振动信号中转频及转频的倍频所对应的时域区段内,1号陀螺仪的平均能量都低于或等于其他三个陀螺仪的平均能量,结合之前滑行时间测试与频域分析结果,可以将1号陀螺仪作为正常陀螺仪,其在时域上特征频率所处区段内的小波方差则可以作为比较其他三个故障陀螺仪的参照。除1号陀螺仪平均能量较为稳定外,其他三个陀螺仪在三个频段内的平均能量均有较大波动,尤其3号陀螺仪的平均能量几乎在全频段都远大于1号陀螺仪,4号陀螺仪在频域图中转频倍频处的能量虽然相对不大但是通过小波分析可以看出在fN和4fN的区段内的振动能量却很大,根据滚珠轴承振动特征频率,可以判定4号陀螺仪滚珠轴承出现磨损的可能性很大。对上述结论进行总结可得:2、3、4号陀螺仪轴承存在故障。

3 结果验证

为验证基于振动信号分析的故障诊断的结果可行性,下面通过对故障陀螺仪2、3、4号陀螺仪进行拆解,分别对陀螺仪滚珠轴承的内外滚道以及滚珠的故障情况进行检测。检测仪器选用的是Nikon研究级体视显微镜SMZ25。

对故障诊断结果中,存在明显故障的2、3、4号陀螺仪进行拆解,然后利用显微镜分别对其滚珠轴承中的内外滚道以及滚珠进行探伤成像。可以发现在陀螺仪2、3、4号的轴承外滚道上均存在不同程度的擦伤,依次分别如图10(a)、10(b)、10(c)所示；陀螺仪2号的滚珠存在锈蚀的情况、陀螺仪3号的滚珠存在明显的磨损,依次如图11(a)、11(b)；陀螺仪2、3、4号的内滚道均存在轻微的锈蚀情况,如图12(a)、12(b)、12(c)。

图10 陀螺仪滚珠轴承外滚道故障图

图11 陀螺仪滚珠轴承滚珠故障图

图12 陀螺仪滚珠轴承内滚道故障图

由上述探伤结果可知,陀螺仪2、3、4号的滚珠轴承均存在不同程度的故障,与故障诊断的结果一致,证明了故障诊断结果的有效性。

4 结语

综合上述振动信号分析、故障诊断实验及实验证验,本文所提出的基于振动信号检测、频域和小波时域分析的方法对于动力调谐陀螺仪实验样本的故障预测分析结果,与滑行时间测试和显微镜探伤结果对比验证,可得故障预测结果与实验验证结果一致,由此可以证明该方式进行故障诊断能实时有效地对动力调谐陀螺仪滚珠轴承故障进行定位预测。