基于双线性插值法的比例方向阀死区补偿方法

吉星宇, 郝惠敏, 杨 凯, 王 鹤, 李 斌, 黄家海

(1.太原理工大学 机械与运载工程学院，山西 太原 030024；2.太原卫星发射中心技术部，山西 太原 030027)

引言

比例方向阀作为电液系统中的重要元件，其作用是连续成比例控制液压执行器的工作速度、方向、位置和输出力的大小[1-3]。但当电液比例方向阀处于零位时，不能够线性地响应控制信号，即产生较大的死区[4]，对比例方向阀的静动态性能产生严重影响[5]。为了获得良好的控制效果，模糊控制[6-10]、步进控制[11]、 神经网络控制[12-14]、 滑膜控制[15-16]等越来越多的智能控制算法和技术应用于死区补偿，以减少死区对控制效果的影响。

汤霞清等[17]提出了一种基于自适应模糊逻辑的死区补偿方法，采用归一化状态距离构造了量化因子权函数，设计了对死区进行补偿的量化因子自适应模糊PD控制器，仿真结果表明，该控制器能够有效消除参数时变的死区对控制系统的影响，提高了系统的控制精度，同时保证了系统的良好动态性能。

孟珺遐等[18]提出了一种对比例变量泵死区进行神经网络补偿的方法，建立了死区的逆模型，根据辨识出的系统参数构造被控对象的参考模型，并设计自适应PID控制器。仿真结果表明逆模型抵消了泵的死区，改善了系统的静态性能。

彭熙伟等[19]针对系统的非线性特性，设计不严格依赖于系统精确数学模型且有较强抗干扰能力的迭代学习算法，同时针对系统的变死区特性，设计能够基于误差和误差变化率在线调整死区补偿量的模糊死区补偿算法。迭代学习算法和模糊死区补偿算法的综合使用有效地改善由于系统非线性及时变性所带来的影响。

上述研究成果多集中于含位移传感器的电液比例伺服元件，而鲜有针对无位移传感器的电液比例伺服元件的死区补偿方法，所以找到一种合适的方法对无位移传感器的电液比例伺服元件进行死区补偿，改善其死区非线性，提高其控制性能具有重要的意义。

针对上述问题，提出了基于双线性插值的死区补偿方法，阀的进、出口压差和输入电压信号作为自研发DSP控制器的输入，由控制器内的双线性插值程序[20]对输入信号进行校正，并输出PWM波，驱动电磁阀，控制阀口开度，达到死区补偿的目的。

1 死区补偿原理

理想情况下，比例方向阀的阀口输出流量为：

qp=f(u,Δp)

(1)

式中，Cd—— 阀口流量系数

w—— 阀口面积梯度

x—— 阀芯位移

pi—— 阀入口处流体压力

po—— 出口流体压力

Δp—— 进出口流体压差，其中Δp=pi-po

umin—— 死区阈值

umax—— 最大输入电压

u—— 输入电压，其中x=ku，

k—— 比例电磁铁增益

由式(1)可知，在理想状态下的阀口输出流量曲线如图1中的曲线1所示，当ui≥umin时，输出流量曲线是一条线性曲线。

图1 静态流量曲线图

死区补偿的原理为：假设Δp=Δp0，输入达到最大值umax时，输出流量最大值为qmax，则补偿后的期望流量曲线如图1中的曲线2所示，曲线2的方程,如式(2)所示:

(2)

当输入为ui0时，根据式(2)可知，此时的期望流量：

(3)

根据补偿前阀的流量曲线qp=f(u,Δp)可得输出流量为qi0时，补偿前的输入电压为:

ui1=f-1(qi0,Δp)

(4)

此时，若将ui1作为ui0的校正电压值，驱动电磁阀，则阀的输出流量就可以达到期望输出流量qi0，这样就达到了死区补偿的目的。

2 基于双线性插值原理的死区补偿策略

在实际应用中，如果直接使用逆反函数ui1=f-1(qi0,Δp)求取校正电压，则需要精确的比例方向阀数学模型，而大多数情况下，都是用简化后的数学模型求取逆反函数，这样存在诸多问题。如文献[21]所示，将比例方向阀死区模型简化为死区段和线性段的组合，提出了无须位移反馈的线性死区补偿策略，试验结果表明该策略虽然能够减小比例方向阀输出流量死区，但是出现了流量提前饱和的问题。

所以本研究不直接用简化后的数学模型求逆反函数进行校正，而是依据式(1)中，压差-输出流量-输入电压存在线性关系，提出基于双线性插值原理的死区补偿策略代替逆反函数求取校正电压。

插值法根据补偿前阀的流量数据，插值计算出期望流量对应的输入电压，并以此电压驱动电磁阀工作，达到死区补偿的目的。

首先通过试验得到不同压差下的期望流量曲线，这是对输入电压进行校正的基础。具体步骤为，将输入电压设为最大电压umax，驱动电磁阀，并不断改变进出口压差，得到(umax,qmax0)，…，(umax,qmaxi),(umax,qmax(i+1))，…，(umax,qmaxn)等有限个点，构建期望流量曲线簇，如图2所示。

图2 期望流量曲线簇

虽然只获取了有限个不同压差下阀的最大流量数据，但是其他压差下的最大流量可以通过线性插值的方法推导。如当压差为Δp=Δpa时，假设Δpa的2个相邻压差为Δpi和Δpi+1，对应的最大流量为qmaxi和qmax(i+1)，则Δp=Δpa时的最大流量为：

(5)

则Δp=Δpa，期望流量曲线为:

(6)

其次获取不同压差下，阀的输入电压与输出流量的关系。具体步骤为设定压差为Δp=Δp0(压差最小为1 MPa)，输入连续电压，获取点(u01,q1)，(u02,q2)，…(umax,qmax0)，依此类推获取Δp=Δpn下的点(un1,q1)，(un2,q2)，…(umax,qmaxn)，如此获取有限个阀的输入电压与流量关系后，则可以构建出补偿前Δp-qp-u的关系表，如图3所示，横坐标表示流量q，纵坐标表示压差Δp，横纵坐标轴的交叉点代表对应流量和压差下补偿前的输入电压值u。

假设此时Δp=Δpa，输入为ui0，要对ui0进行补偿，首先代入式(6)，计算出该输入下的期望流量：

(7)

则此时，求Δp=Δpa，u=ui0时的校正电压问题就转化成了求Δp=Δpa，qp=qi0时，补偿前输入电压值ui1的问题。由于我们已经构建出了补偿前Δp-qp-u的关系表，只要进行双线性插值计算，就可以得到Δp=Δpa，qp=qi0时，补偿前的输入电压。

假设图3中Mint就表示Δp=Δpa，qp=qi0，而M1，M2，M3，M4是所记录数据中最为接近Δp=Δpa,qp=qi0的4个点。M1(Δp1,q1)，M2(Δp2,q2)，M3(Δp3,q3)，M4(Δp4,q4)表示对应压差和流量值补偿前的输入电压值，且分别为u11，u12，u22，u11。现要求Mint(Δpa,qi0)，即补偿前Δp=Δpa，qp=qi0时的输入电压值ui1。

图3 双线性插值原理

则插值计算过程为，先在q轴进行一次插值：

(8)

(9)

再在Δp轴进行一次插值：

(10)

将式(8)、式(9)带入到式(10)中，就可以得Δp=Δpa，qp=qi0时，补偿前阀的输入电压ui1，以ui1对ui0校正，驱动电磁阀，就可以达到死区补偿的目的。

3 在DSP控制器中的补偿过程

自行研制的DSP数字控制器，硬件部分包括输出电路，电流检测电路，AD采样电路，微控制器以及外围电路等。控制算法则是以C语言的形式写入到微控制器中，所以补偿前Δp-qp-u的关系表以二维数组的形式存在于控制器中，进行补偿时，通过查表的方式，得到Δp=Δpa，qp=qi0的4个相邻点，然后进行插值计算，得到校正电压，校正电压按比例调节PWM波占空比，调节后的PWM波通过输出电路驱动电磁阀工作。

在试验中发现，如果采用正行程补偿前Δp-qp-u的关系表，进行返行程补偿时会出现较大误差，原因在于阀的滞环比较大，正、返行程的静态流量特性曲线差别较大。所以在微控制器中有2个关系表，分别对应正、返行程，补偿过程如图4所示。

图4 补偿过程流程图

4 试验结果分析

测试原理如图5所示，比例方向阀为自制试验阀，额定流量为30 L/min(1 MPa压差)；采用ATOS的E-ATR-5/250/I型压力传感器(量程范围为0～25 MPa)对主阀入口处压力pi进行测量；采用E-ATR-6/100/I型压力传感器(量程范围为0～10 MPa)对主阀出口处压力po进行测量；使用齿轮流量传感器SCVF-150-10-07(最大量程为150 L/min)测量比例方向阀的阀口输出流量；NI-USB-6343采集卡采集传感器信号；AFG1022信号发生器输出0～10 V的控制信号；控制器采用自制的，以TMS320F28335为核心的控制板。在试验时，将比例方向阀的进出口相连，比例方向阀处于空载状态，溢流阀用来设定进口压力，则溢流阀设定压力即为进、出口压差。

图5 测试原理图

4.1 静态特性测试

如图6所示，输入信号为0.05 Hz，幅值为10 V的三角波信号。分别设定进、出口压差为2 MPa和4 MPa，补偿前的阀口流量静态特性曲线如图7所示；补偿后与补偿前的阀口流量静态特性曲线对比图如图8所示；补偿前后滞环曲线如图9所示。

图6 输入电压曲线图

从图7可以看出，补偿前，阀的死区很大，2 MPa压差下，阀的正、返行程死区分别为44%和34.8%；4 MPa 压差下，阀的正、返行程死区分别为44.4%和35.6%。如图8所示，对输入电压进行双线性插值补偿后，能够有效的减小死区，并且没有造成明显的过补偿。补偿后，2 MPa压差下，正行程0时流量过补偿约为0.16 L/min，死区大小约为2%；返行程0时流量过补偿约为0.11 L/min，无死区；4 MPa压差下，正行程0时流量未出现过补偿，死区大小为1.6%；返行程0时流量过补偿为0.2 L/min，无死区。

图7 补偿前的阀口静态流量曲线

比较补偿前后阀的流量曲线的线性度发现，补偿后的线性度要小于补偿前的线性度。补偿前阀在整个输入区间上分为非线性段和线性段两部分，因此计算补偿前的线性度时，只计算线性段的线性度，而计算补偿后的线性度时，则计算整个输入区间的线性度。以2 MPa压差下试验结果为例，补偿前正行程阀的线性度为7.61%，返行程阀的线性度为10.04%；补偿后正行程阀的线性度为2.93%，返行程阀的线性度为3.40%。

图8 补偿后与补偿前的阀口静态流量特性曲线对比图

从图9可以看出，补偿前阀的静态流量曲线滞环比较大，补偿后阀的静态流量曲线滞环明显减小，原因在于补偿后输入信号得到了校正，使阀的输出流量能够达到该输入下的期望流量值，而正、返行程的期望流量曲线是一致的，即同一输入信号的期望流量是一致的，这样就造成补偿后正、返行程同一输入信号下阀的输出流量是一致的。

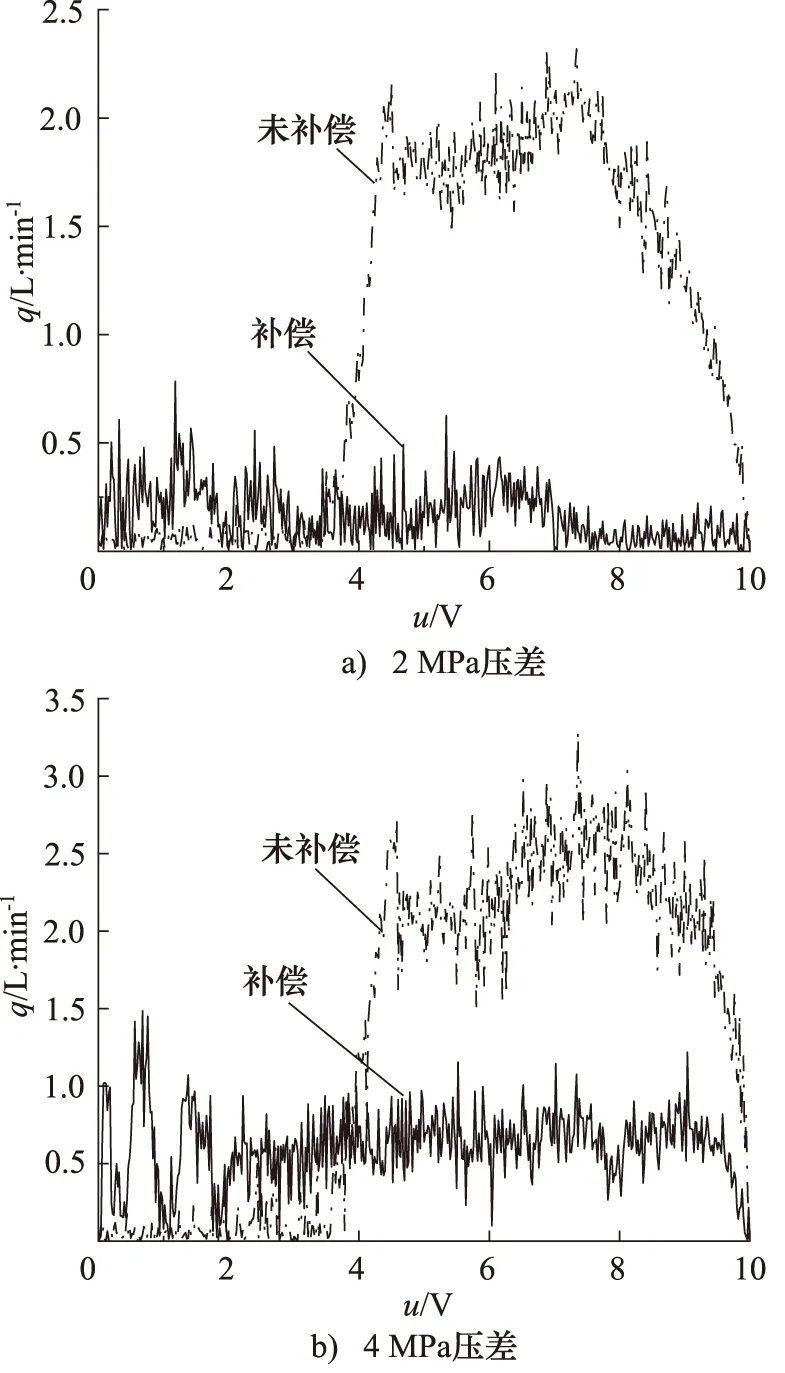
图9 滞环分析

4.2 动态特性测试

主阀进、出口压差不变，分别在补偿后和补偿前的情况下，施加周期为20 s，幅值为10 V的方波信号。从图10可以看出补偿后和补偿前在输入上升阶跃时，都没有出现明显超调，下降阶跃时，补偿后的响应速度要快于未补偿；2 MPa压差下，补偿后提前120 ms达到流量最低值；4 MPa压差下，补偿后提前300 ms达到流量最低值。至少说明了补偿后并未降低阀的动态性能。

图10 阶跃响应测试

5 结论

(1) 研究结果表明所提出的基于双线性插值原理的死区补偿方法具有可行性；

(2) 进行死区补偿后，死区减小，就静态性能而言，阀在整个输入区间具有良好的线性度，且滞环明显减小；动态性能而言，补偿后并未降低阀的动态性能；

(3) 插值补偿的目的是将阀的静态流量曲线变为一条无死区，且在整个输入区间上线性度都较好的曲线，当输入电压为0时，校正电压正好为死区电压，但若是在插值表中记录的死区电压偏大，就会导致过补偿。所以，为了提高双线性插值死区补偿的效果，需要建立较为准确的Δp-qp-u关系表。