HVDC系统高精度闭环动态相量仿真模型

单俊儒，刘崇茹，李欢，魏伟

(1. 新能源电力系统国家重点实验室(华北电力大学)，北京102206；2. 直流输电技术国家重点实验室(南方电网科学研究院)，广州510663)

0 引言

随着高压直流输电(high-voltage direct-current, HVDC)技术在我国的迅速发展[1 - 2]，电力系统的非线性化特征日益明显，这一变化也对系统的建模和仿真提出了新的要求[3 - 6]。因此，亟需对高压直流输电系统建立合适的数学模型，使其能够准确反映各种工况下系统的稳态和暂态特性。

目前，根据不同的精度需求和应用场景，HVDC系统主要有以下3种等值模型：电磁暂态模型[7 - 9]、准稳态模型[10 - 13]和动态相量模型[14 - 18]。通常认为电磁暂态模型计算精度高，但其计算速度受系统规模的限制比较明显，实时仿真对硬件性能的要求也相对较高[9]；准稳态模型使用线性代数方程组表征交直流系统间的电气量关系，计算速度快。但该模型建立在换流器各换相过程对称且无谐波的前提下，并不适用于不对称故障[12]。因此，作为对准稳态模型的改进，建立适用于不对称故障的HVDC系统动态相量模型，并在保证计算速度的同时尽可能地提高模型精度成为了目前相关研究的重点。

动态相量模型以时域信号的傅里叶分解为数学基础，通过忽略不重要的频率分量对系统进行简化并增大仿真步长，是一种仿真速度和精度都介于电磁暂态模型和准稳态模型之间的相量模型。文献[15]基于三相对称开关函数，推导了适用于正常运行工况的换流器动态相量模型。在此基础上，文献[16]和文献[17]分别考虑了交流不对称情况下换相过程偏移和系统谐波的影响，提升了换流器动态相量模型对于不对称故障的计算精度。文献[18]在建立换流器动态相量模型后，继续对直流线路和控制系统进行建模，实现了HVDC全系统的闭环计算。对上述研究进行总结可以发现，单独的换流器动态相量模型虽能取得比较精确的计算结果，但其只能实现开环计算，仿真时除交流三相电压外仍需外界输入控制量和直流电流数据。而现有HVDC全系统闭环模型仍然假定开关函数三相对称，无法对不对称故障进行精确计算。同时，所有开环和闭环动态相量建模皆没有考虑换流变压器的影响，或只使用了理想变压器模型，缺少对于换流变压器的动态相量建模研究，这直接影响了阀侧交流电压的计算精度，进而为仿真引入了较大误差。

因此，现阶段亟需构建HVDC系统的高精度闭环动态相量仿真模型。针对这一问题，本文首先考虑了不对称故障下换相电压的偏移并对传统开关函数进行修正。随后，将得到的改进开关函数模型与动态相量方法结合起来，同时计及系统谐波特性，建立了适用于不对称故障的改进换流器动态相量模型。在此基础上，进一步考虑换流变压器的影响，对HVDC全系统进行动态相量建模并重构了闭环仿真流程，提高了计算精度。基于CIGRE标准直流系统进行了动态特性的仿真计算，结果进一步证明了所建高精度闭环动态相量仿真模型的有效性。

1 传统动态相量模型

动态相量法[15]指出，对于时域信号x(τ)，在任一时间窗(t-T,t)内，其傅里叶变换与反变换为：

(1)

式中：ω=2π/T；〈x〉k为时域信号的k阶傅里叶系数，也被称为k阶动态相量；τ为时间变量。动态相量具备式(2)所示共轭、乘积和微分特性。

(2)

式中上标*表示相量的共轭。因此，在动态相量模型中时域信号x(τ)通常由式(3)进行计算。

(3)

式中Re表示取实部。

在此基础上，动态相量法通过调制理论表达换流器交直流侧的电压电流关系[12]，对于图1所示的6脉波换流器，其电压电流计算公式如式(4)所示。

图1 6脉波换流器示意图

(4)

式中：vd为直流电压；Ua、Ub、Uc为换流器交流侧的三相电压；Sua、Sub、Suc为三相电压开关函数；ia、ib、ic为换流器交流侧三相电流，id为换流器直流侧直流电流；Sia、Sib、Sic为三相电流开关函数。根据式(2)和式(4)，可得换流器动态相量模型为：

(5)

(6)

式中：m=a、b、c,分别表示a相、b相和c相；根据需要忽略相电压和开关函数的高频分量，可对换流器动态相量模型进行不同程度的简化。

2 改进的换流器动态相量模型

为提高换流器动态相量模型在不对称故障下的计算精度，首先讨论了交流不对称情况下实际触发角和换相角的计算方法，重新推导了开关函数的模型。在此基础上，充分考虑交流和直流系统的谐波特性，建立了适用于不对称故障的改进换流器动态相量模型。

2.1 实际触发角与换相角的计算方法

现阶段高压直流输电工程中，控制系统以锁相环锁定的自然换相点为基准延迟αord电角度后向对应换流阀发出触发脉冲，αord为触发角指令值。但不对称故障发生时，电压幅值和相位的变化会使自然换相点发生偏移，因此实际换相过程的触发角需在指令值的基础上进行修正。

2.1.1 触发角指令值计算方法

在HVDC系统中，触发角指令值αord由控制系统极控级计算得到。依照CIGRE标准直流系统进行极控级建模，整流侧采用定电流控制，逆变侧采用定电流和定熄弧角控制。同时，为了保证故障的顺利恢复，控制系统包含有低压限流(VDCOL)环节。各环节的配合关系如图2所示。

图2 HVDC控制系统示意图

图2中下标“R”和“I”分别代表整流侧和逆变侧；γ为逆变侧熄弧角；Iorder和γmin分别代表直流电流指令值和最小熄弧角限制，二者为预先设定的常数；γerr为电流偏差控制输出的熄弧角增量。由图可知，各环节分别采集当前时刻不同的一次系统电气量，经过一系列的计算后分别输出整流侧和逆变侧的触发角指令值。

本文依照CIGRE标准系统提供的控制器参数对各控制环节依次列写微分方程，并采用数值积分方法获得控制系统的响应。在实际的工程实用中，控制方法和控制参数可能会出现变化，但本模型的建模思路及求解方法仍不失普适性。

2.1.2 延迟触发角修正与换相角计算

图3所示为n相到m相换相的电压偏移示意图。

图3 实际换相电压偏移情况

图3中Un、Um为系统正常对称运行时n相和m相的交流电；Pmn即为锁相环锁定的自然换相点；U′n、U′m分别为n相和m相发生不同程度故障后的畸变电压；P′mn为偏移后的实际自然换相点；Δφmn为自然换相点的偏移量，该偏移量以P′mn滞后Pmn为正。如前文所述，实际工作过程中，HVDC阀控制级以Pmn为基准延迟αord后向对应阀发出触发脉冲，脉冲以粗实线表示。

实际触发角应为阀导通时刻相对于实际换相点P′mn的角度。如图3(a)所示，若n相电压畸变为U′n，此时实际自然换相点前移至P′mn，偏移量Δφmn<0<αord。当触发脉冲到达时，m相电压大于n相电压，换流阀承受正压导通，因此实际触发角αmn=αord-Δφmn；但若m相电压如图3(b)所示畸变为U′m，此时实际自然换相点后移，且偏移量Δφmn>αord。触发脉冲到达时，m相电压仍然小于n相电压，相应的换流阀无法导通。直至自然换相点P′mn，阀承受正压立即导通，因此实际触发角αmn=0。综上，n相到m相换相的实际触发角αmn可写为如式(7)所示的统一形式。

(7)

进一步地，各换相过程的换相角也需按式(8)进行分别计算。

(8)

式中：Emn为换相电压有效值；Xr为换相电抗。

2.2 改进开关函数模型

为实现不对称故障下换流器通断过程的准确描述，本文在文献[13]方法的基础上，增加对于延迟触发角的考虑，将电压(电流)开关函数分解为基本分量Sn、延迟触发分量Sm和电压(电流)开关函数换相分量Suμ(Siμ)的叠加，如图4所示。

按图4所示坐标系对各分量进行傅里叶分解，得到各分量的k阶傅里叶系数如式(9)所示。

在此基础上，本文为各换相过程独立地分配了延迟触发角αmn和换相角μmn。以a相开关函数为例，其包含有ca换相和ab换相两个换相过程，因此，a相开关函数各分量的k阶动态相量如图(10)所示。

因此，a相电压开关函数Sva和电流开关函数Sia的k阶动态相量可由相应分量的叠加求出，如式(11)所示。

b、c相开关函数的求解方法与a相相同，区别在于b相开关函数包含的换相过程为ab换相和bc相，而c相开关函数包含的换相过程为bc换相和ca换相。除此之外，b、c相开关函数的k阶动态相量在相位上分别滞后和超前a相开关函数2πk/3。

(9)

(10)

(11)

2.3 换流器动态相量模型

文献[14]指出，为确保不对称故障时的计算精度，直流电压需考虑0次和2次动态相量，而交流电流则需考虑1次和3次动态相量。因此，结合式(5)，换流器直流电压的动态相量求解公式如式(12)所示。同理，根据式(6)，交流三相电流的动态相量值求解如式(13)所示。

进一步地，根据动态相量的定义，可将动态相量值转换至时域值，如式(14)所示。

(12)

(13)

(14)

式(12)—(14)共同组成了换流器动态相量模型。必须指出的是，式(12)中与开关函数直接相乘的交流电压Um为换流变压器阀侧交流电压，该阀侧电压与直流电流相耦合，无法作为独立变量输入仿真模型。因此，本文使用换流变压器母线侧交流电压作为系统输入，并在第3节中对换流变压器进行了动态相量建模，重构了HVDC全系统的闭环仿真流程。

3 HVDC全系统建模与闭环仿真流程

在建立换流器动态相量模型的基础上，进一步对换流变压器和直流线路加以分析，重构了仿真流程，提升了闭环计算的精度。

3.1 换流变压器模型

为提高计算精度，有必要使用考虑损耗的换流变压器模型代替无阻抗的理想变压器模型。换流变压器m相等效电路如图5所示。

图5 换流变压器等效电路

图5中，Usm为换流变压器母线侧m相交流电压，Um为变压器阀侧m相交流电压；LT为换流变压器每相的等值电感；ZHVDC为整个HVDC系统的等值阻抗，所有数据均已归算至二次侧。由此可得换流变压器基本方程的动态相量表达式如式(15)所示。

〈Usm〉1=〈Um〉1+jωLT〈im〉1

(15)

由前文推导，交流电流im可看作直流电流经电流开关函数调制得到。因此将式(13)代入式(15)，同时出于加快模型计算速度的考量，忽略直流电流的二次分量，只考虑占主导的0阶动态相量，经整理可得：

〈Um〉1=〈Usm〉1-jωLT〈id〉0〈Sim〉1

(16)

式(16)阐明了阀侧交流电压与直流电流的耦合关系。进一步地，将式(16)代入式(12)，可得直流电压的0阶动态相量计算公式如式(17)所示。

(17)

式(17)表明，当考虑换流变压器电感对于阀侧电压的影响时，换流站可以等效为压控电压源串联阻抗的形式，如图6所示。易知，当使用理想变压器模型时，Zeq=0，此时换流站相当于无内阻的压控电压源〈vsd〉0。

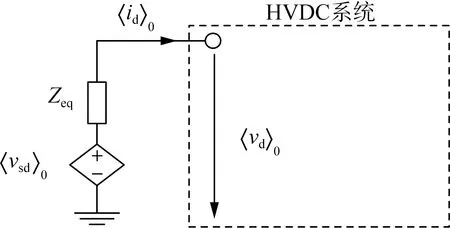
图6 换流站等效模型

3.2 直流线路模型

相比于分布参数线路模型，使用图7所示的T形电路对直流线路进行等效可以在保证计算精度的同时大大加快计算速度。

图7 直流线路等效模型

图7中，Rd、Ld、Cd分别表示直流线路的电阻、电感和对地电容。等效模型涉及的微分方程组为：

(18)

式中：vdR、vdI为整流侧和逆变侧的直流电压；idR、idI为整流侧和逆变侧的直流电流；vc为线路中点对地电容电压。如前文所述，直流系统主要考虑0次和2次动态相量，因此结合式(2)、式(18)可改写为式(19)—(20)。

(19)

(20)

3.3 全系统闭环仿真流程

将式(17)分别应用于整流侧和逆变侧，并与式(19)联立，即可得到如图8所示的HVDC全系统0阶动态相量等效电路。图中，各电气量下标中“R”、“I”分别表示整流侧和逆变侧。

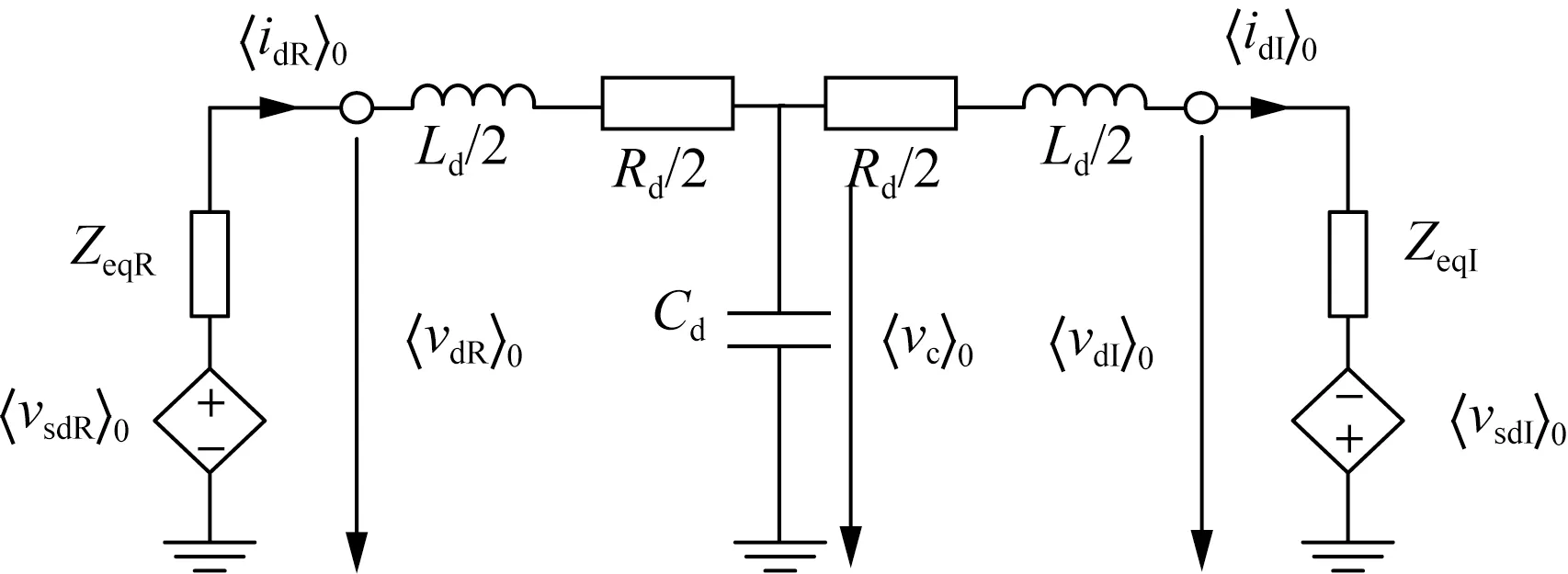
图8 HVDC全系统等效模型

求解图8所示电路即可得到整流侧和逆变侧各自的直流电压〈vd〉0和直流电流〈id〉0。 进一步的，将〈id〉0代入式(16)即可求出阀侧交流电压的一阶动态相量〈um〉1。 随后，按式(12)和式(20)继续对2阶动态相量进行求解，并按式(14)将计算结果转换至时域，即可完成HVDC全系统的动态相量计算。

至此，本文已完成HVDC系统高精度闭环动态相量(high-precision closed-loop dynamic phasor, HPCL-DP)仿真模型的建立，本模型的仿真流程如图9所示。

图9 仿真过程流程图

由于实现了高压直流全系统的闭环计算，HPCL-DP模型所需输入仅为整流侧和逆变侧的交流母线电压。同时，由于考虑了换相过程不对称和换流变压器的电压损耗，本模型对于各类型故障都有较高的仿真精度。

4 算例分析

将所提HPCL-DP模型应用于CIGRE Benchmark标准系统，并将计算结果与PSCAD电磁暂态仿真结果进行对比，进一步证明本模型的有效性。

本文在整流侧和逆变侧共设置了4组故障类型。其中，为防止发生换相失败情况，也为了增加故障场景的多样性，逆变侧故障设计为经过渡电阻接地。计算时交流系统频率为50 Hz，仿真步长均设置为100 μs。故障的详细描述如表1所示。

表1 故障类型描述

图11 直流电流结果对比

结合前述推导过程，本文选取直流电压和直流电流作为评价模型精度的关键电气量，分别输出各类型故障下整流侧直流电压vdR和逆变侧直流电流idI的时域值进行对比，结果如图10—11所示。

图10 直流电压结果对比

图中，PSCAD和HPCL-DP分别表示电磁暂态仿真结果和本文所建高精度闭环动态相量模型仿真结果；vdI、idI分别为逆变侧直流电压和直流电流；vdR、idR分别为整流侧直流电压和直流电流。

仿真图像表明，在计及换相电压偏移和换流变压器的电压损耗后，本文所建HPCL-DP模型精度较高，其仿真结果能够在各类型故障下很好地跟随电磁暂态仿真结果。

为进一步验证模型的仿真性能，本文使用耗时系数λ和残差相似度φ对仿真结果进行分析。其中，耗时系数定义为HPCL-DP模型计算时间与PSCAD计算时间的比值。残差相似度的计算公式如式(21)所示。

(21)

式中y和z分别代表电磁暂态仿真结果和所提HPCL-DP模型仿真结果。计算各故障下耗时系数和直流电压电流的残差相似度，结果如表2所示。

由表2可知，所提HPCL-DP模型较电磁暂态模型具有更快的仿真速度。同时已有研究指出，残差相似度大于80%，模型能够满足仿真误差要求[19]。而本文所建模型所有仿真结果的残差相似度皆在93%以上，因此所建HPCL-DP模型能够在各类型故障下对HVDC系统进行快速精确的闭环仿真计算。

5 结论

本文通过对高压直流输电系统各元件进行详细分析，重构了HVDC闭环动态相量模型和仿真流程，并利用算例验证了其有效性，取得如下结论。

1)本文通过综合考虑系统谐波和换相电压偏移的影响，构建了适用于不对称故障的换流器动态相量模型，实现了对各类型故障下交直流系统电气量关系的准确表达，突破了传统换流器模型的局限性。

2)本文对换流变压器进行动态相量建模，充分考虑了变压器损耗对于阀侧电压的影响，进一步提高了计算精度，也为研究变压器参数对于HVDC系统动态性能的影响提供了可能。

3)从控制变量的角度出发，本文在算例分析中对动态相量模型和电磁暂态模型使用了相同的仿真步长。但由于动态相量模型忽略了不重要的频率分量，因此在工程实用中可以使用更大的仿真步长，从而获得更高的计算速度。

4)本文对HVDC全系统进行了建模推导，因此只需输入交流母线电压数据，即可自行完成闭环计算并实时输出仿真结果。这大大拓宽了模型的使用前景，只需改变其输入量即可应用于不同的场景。例如输入现场实测的交流母线电压波形，则该模型可以实现系统响应的快速跟踪。如输入的电压为交流系统的预测故障电压，则该模型可被用于安全裕度指标的快速评估。

5)在以换相失败为代表的某些暂态情况下，开关函数可能无法反映换流阀的开关状态，此时本模型并不适用。此外，理论上采用较高的阶数虽可以进一步提高模型的计算精度，但计算量和仿真耗时也会随之增加，从而使动态相量模型失去了原有的优势。因此在少数对暂态过程精度要求极高的场合或在研究高频谐波扰动对电网特征影响时，仍需对动态相量模型进行原理上的改进。