一维变参数溶质运移模型的数值研究

蔡松柏，邵明安，齐丽彬

(1.湖南师范大学 资源与环境科学学院,湖南 长沙 410081;2.中国科学院 水利部水土保持研究所,陕西 杨凌 712100;3.三门峡职业技术学院 生化工程系,河南 三门峡 472000)

由于工农业生产、雨水径流冲刷和人为因素等作用，造成水流中溶质瞬间注入或连续注入从而引起河流或地下水的水质改变。研究溶质瞬时注入或连续注入情况下不同时刻溶质浓度在河流或地下水流中的分布状况、及不同位置时溶质浓度随时间的变化情况，可通过数学模型来模拟或预报水质在时间或空间的变化，达到为水环境质量预报、控制和水资源管理服务的目的[1-22]。

数值模拟水流溶质运移的主要方法有有限元法、边界单元法、有限差分法和其他数值法等。由于进行水质模拟过程中涉及的参数在不同的时间和空间上变化较大，在水质模拟过程中，会造成数值弥散、数值波动和计算量巨大等问题。国内主要的研究有徐玉佩[2-3]用Galerkin法推导了二维地下水运动的有限元方程和溶质运移有限元方程，并编制了计算程序应用于明沟排水和田面保持淹灌水层情况下的冲洗种稻改良盐碱地的分析,还与现有解析解和实验资料进行了对照。徐玉佩还用水动力弥散理论进行了地下水中水盐动态的研究,可直接用于盐碱地的预防和改良。黄康乐[4]则提出了一种求解二维饱和-非饱和溶质运移问题的交替方向特征有限单元法(ADCG)，在克服数值弥散、数值波动和提高计算速度方面具有显著的优越性。张效先等[5]提出了一种计算地下水中溶质运移的数值法，将多维问题分解成几个一维问题, 减少了计算工作量, 并消除了数值波动现象,具有较高的精度。冯绍元[6]提出了特征有限元法的基本理论和实施过程,其计算实例表明能消除大部分的数值弥散而又不增加解的振荡性。姚磊华[7]首先基于分步求解的思想, 用广义迎风对偶单元均衡法求解对流定解问题, 对扩散定解问题采用一般的Galerkin有限元法求解, 不仅避免了数值弥散和过量问题, 而且避免了求节点速度这一步, 简化了运算步骤。邱克俭等[8]结合拉格朗日观点的运动坐标与欧拉观点的固定坐标,分别求解对流-弥散方程的对流效应和弥散效应, 并通过与理论解和试验结果做比较，验证了模型的可靠性。任理等[9]采用混合拉普拉斯变换有限单元法求解对流占优的地下水溶质运移问题，能有效地消除数值扩散和过量现象，特别适于大区域地下水污染的长期预报。李焕荣等[10-11]利用广义差分法建立了一维非饱和水流问题的守恒形式的数值模型, 具有计算量小和稳定性好的特点, 其提出的非粘性土壤水中溶质运移问题的守恒混合元格式，精度高且数值稳定。段德宏等[14]以黄河兰州段为例,采用一维稳态河流水质模型,对岸边19个污水排放口及共约32.9 km长的全河段污染状况成功地进行了模拟。徐文彬等[15]根据数值随时间步长变化的特点，提出了针对数值波动、弥散和过量现象的新改进方案，并用实例验证了方法的可行性。何丕文[16]利用一维水质模型，采用有限差分法求解河流中污染物浓度，以淮河淮南段为例进行了验证。马东豪等[17]研究了土壤溶质迁移的两流区与两区模型，结果表明与两区模型相比,两流区模型可以更好地描述优先流情况下的溶质穿透曲线。对于无优先流情况, 连续流输入情况下两个模型的参数一致性较好；而在脉冲输入时一致性较差。国外在溶质运移模型及其数值计算方法上的研究也很多，如JAISWAL等[18]运用Chebyshev配点法求解一维溶质运移问题的数值解。SILAVWE等[19]讨论了某些数值方法用于一维溶质运移模型的参数估计，通过将数值解与试验结果比较，反演溶质运移模型参数。JAISWAL等[20]采用算子矩阵法对多孔介质的非线性微分方程进行了数值分析，该法应用切比雪夫多项式并结合切比雪夫导数运算矩阵和谱配置法对解进行逼近。其优点是可以将这些问题转化为易于求解的代数方程组。CARR[21]利用拉普拉斯变换导出了层状多孔介质溶质运移的新半解析解，该法在相邻层的界面引入表示运移量的未知函数，将多层问题置于拉普拉斯域上分层解决，然后再将其数值反演回时域。ALLWRIGHT等[22]对地下水溶质运移方程在对流明显强于扩散时出现的数值波动提出了两种新的数值近似计算方法，即只适用于对流项的迎风Crank-Nicolson格式和加权迎风-下风格式，并对这些新提出的格式进行了数值稳定性分析和比较。发现如果Crank-Nicolson格式只用于对流项时很合宜。此外，显式加权迎风-下风有限差分格式是对传统显式一阶迎风格式的改进，而隐式加权一阶迎风-下风有限差分格式在给定适当的权重因子时无条件稳定。

本文主要贡献在于对一维溶质对流弥散基本方程，首先，建立了一维溶质运移3种变溶质运移参数模型，即线性变化模型/多项式变化模型、指数变化模型和幂变化模型；其次，采用显式时域差分法成功地进行了溶质浓度时空分布的数值计算，有效克服了很多研究人员遭遇的数值波动、数值弥散和计算量大等难题，并与解析解和实验结果做了对比，验证了该数值方法的正确性；最后，对3种溶质运移参数模型进行了参数分析，获得了3种模型的初步认识。

1 基本原理

研究溶质在水流中的迁移规律，试验测定可采用电解质脉冲示踪法等来进行。电解质脉冲在水流中的运移规律符合溶质对流弥散基本方程，根据夏卫生等[12-13]的研究，其溶质运移参数随水流位置而变化，在大规模的地下水流问题中，溶质运移参数亦会随空间位置而变化。对其溶质运移规律的模拟可采用近似解析解和数值解。

1.1 一维变溶质运移参数对流弥散溶质运移基本方程及定解问题

由邵明安等[1]提出的一维变溶质运移参数对流弥散溶质运移基本方程可写为：

(1)

在脉冲注入时的初始和边界条件可写为：

c(x,0)=c0

(2)

c(0,t≤t0)=c1

(3)

c(0,t>t0)=c0

(4)

c(l,t)=c0

(5)

式中：x为水流方向长度坐标，t为时间，c(x,t)为水流中溶质浓度，l为计算水流长度，t0为溶质脉冲注入的时间，c1为脉冲注入溶质的浓度，c0为水流中溶质的初始和平衡浓度，D(x)为水流中溶质扩散系数，u(x)为水流速度。本文假定D(x)，u(x)为下列3种模式。

1)线性模式/多项式模式

即,线性模式：

D(x)=D0(1+bx/l)

(6)

u(x)=u0(1+bux/l)

(7)

和多项式模式：

D(x)=D0(1+bx/l+cx2/l2)

(8)

u(x)=u0(1+bux/l+cux2/l2)

(9)

2)幂函数模式

D(x)=D0(1+cxb)

(10)

u(x)=u0(1+cuxbu)

(11)

3)指数函数模式

D(x)=D0(1+cbx)

(12)

(13)

式中：b，c，bu和cu为模型参数。

1.2 一维常溶质运移参数溶质对流弥散基本方程的解析解

定义溶质扩散系数和水流速度的平均值分别为：

(14)

(15)

对于式(6)和(7)线性模型，则有：

(16)

(17)

由文献[1]，利用Heavyside阶跃函数，本文首次得到了D(x)=D，u(x)=u时式(1)的解析解为：

(18)

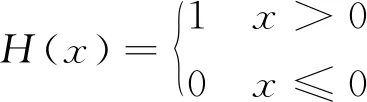
2 理论与列式

2.1 差分网格

由于溶质浓度随时间和空间连续变化，可沿x方向取水流有限长度l作为计算对象，将l分为等间距的n个单元，结点编号为i，i=0,1,2,…,n，步长为Δx=l/n，将时间坐标划分为时间步长为Δt的时段，结点编号为k，k=0,1,2,…,m。

2.2 即时显式差分格式

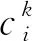
(19)

将式(19)变形，可得差分递进格式：

i=1,2,3,…,n-1

(20)

其中：

(21)

(22)

(23)

3 计算结果与讨论

根据上面的理论基础，利用双精度FORTRAN语言编写程序，分别采用方程(19)所代表的数值方法和方程(18)所代表的解析方法求得溶质浓度分布，以检验数值方法的可靠性。并对不同溶质运移参数变化模式下瞬时注入溶质后水流中溶质浓度的时空分布进行了数值模拟和参数分析。

3.1 一维溶质运移参数线性变化时方程数值解与解析解比较

由夏卫生等[12-13]的试验结果得知，坡面薄层水流的溶质扩散系数及水流速度均随位置而变化。本计算的变溶质运移参数模型采用D(x)=D0(1+bx/l)，u(x)=u0(1+bux/l)。根据夏卫生等[12-13]的试验数据，取D0=5.1×10-2m2/s，b=-0.55，u0=1.02 m/s和bu=0.042。l=3.5 m，t0=0.6 s， 注入溶液浓度c1=0.63，水流起始溶质浓度和平衡浓度c0=0.20，Δt=0.04 sec和Δx=0.025 m，分别求得了水流方向上不同位置处溶质浓度的数值解和近似解析解。

图1给出了数值解、近似解析解与文献[12]实测结果的比较，从图中可以看出两种模拟结果同夏卫生等[12-13]的结果一致，测量曲线和模拟曲线的溶质浓度最大值均呈逐渐减小的趋势；在距离较大处其模拟结果和实测结果吻合较好。近似解析解和数值解能较好地吻合，特别是距离越大，二者吻合得越好。这说明显式差分法求解溶质运移方程的精度已经能够达到要求。

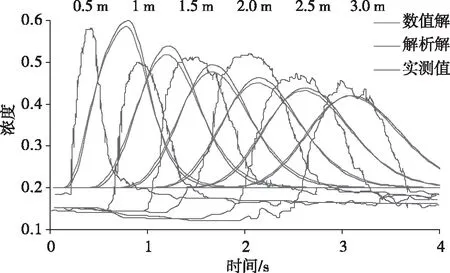
图1 模拟结果和实测结果比较

表1给出了一维常溶质运移参数模型在脉冲注入后溶质浓度随深度、时间变化的数值解式(20)与解析解式(18)的比较，其中，常溶质运移参数D0=5.1×10-2m2/s，u0=1.02 m/s，其余计算参数同图1取值，从表中可以看出二者吻合非常好，说明了数值方法是可靠的。

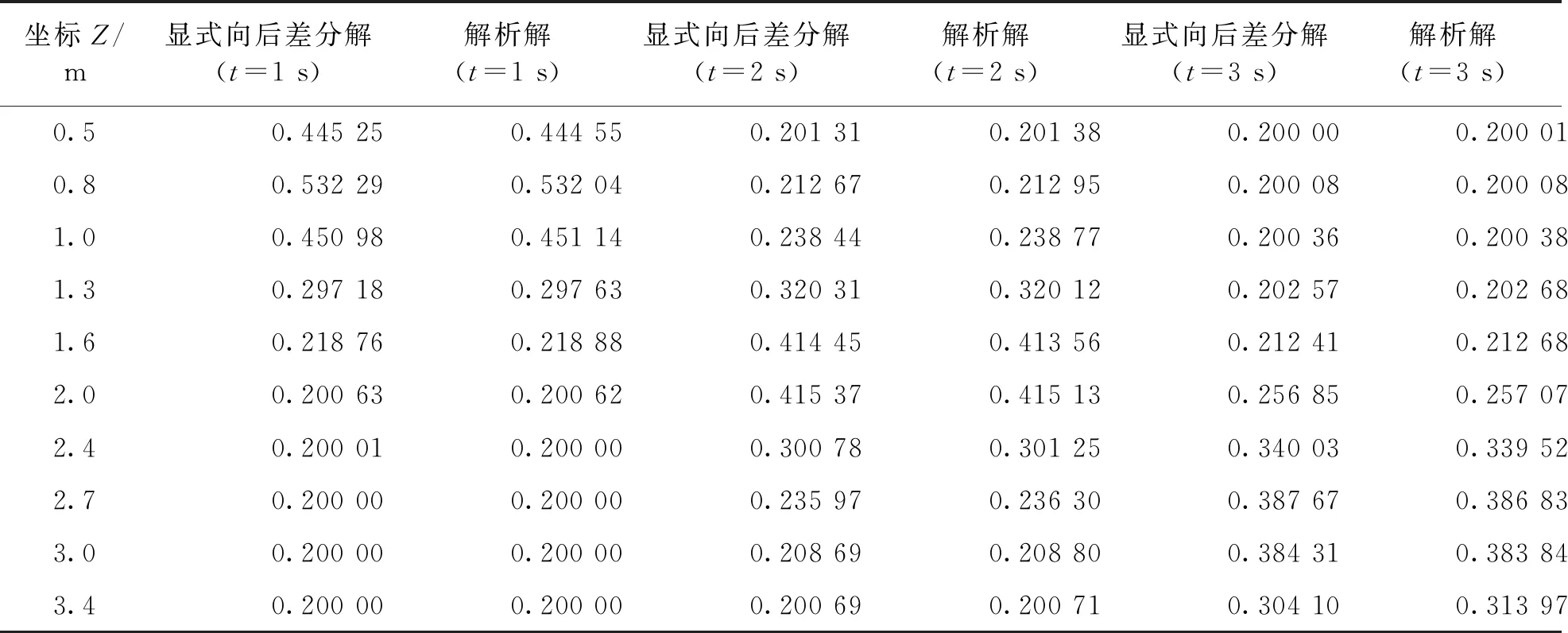
表1 常系数模型注入脉冲溶质后溶质浓度变化的数值解与解析解的比较

由图1和表1可知，常溶质运移参数一维溶质运移基本方程的解析解与变溶质运移参数一维溶质运移基本方程的数值解基本一致。因此，求解溶质运移基本方程可以采用本文数值方法。

3.2 一维溶质运移参数多项式变化时的数值结果

给定D0=0.03 m2/s，u0=1.00 m/s，计算水流位置l=3.5 m，脉冲注入溶质浓度时间t0=0.6 s，注入溶液浓度c1=1.00，水流起始溶质浓度和平衡浓度c0=0.20，计算步长Δt=0.04 sec和Δx=0.025 m,当式(8)和(9)中模型参数c=0.1，b=±0.6,±0.4,±0.2，对cu,bu和c,b同步一样取完全相同值时，其数值解法求出的溶质浓度沿水流位置的分布规律如图2所示，图2中c和b同时代表cu,bu和c,b的取值。从图2可以看出，c,cu的零值附近微小变化对溶质浓度分布影响较计算方法带来的差别要小。c,cu值一定时，随着b,bu从-0.6到0.6的增加，某时刻溶质浓度位置上的分布，其峰值和峰宽增加，波峰位置滞后。时间越长，这种浓度分布的波峰变化规律越明显。在1 s时间以内，本文对b,bu和c,cu的不同取值对溶质浓度分布影响不大。

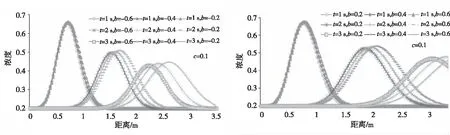
图2 多项式模式溶质参数的一维溶质运移浓度分布及比较

3.3 一维溶质运移参数幂函数变化时的数值结果

溶质运移参数采用式(10)和(11)的幂函数变化模型，给定模型参数b=2且c=±0.9,±0.6,±0.3下，cu,bu和c,b取值完全相同，其余计算参数D0，u0，l，t0，c1，c0，Δt和Δx同以上多项式模式中参数的取值，一维溶质运移浓度分布数值解如图3所示。图3表明，参数中指数b/c，bu/cu较大时，c,cu值的大小对溶质浓度分布的影响较小，时间越短，这种影响越小。

图3 幂函数模式溶质参数的一维溶质运移浓度分布及比较

3.4 一维溶质运移参数指数变化时的数值结果

图4所示为溶质运移参数模型采用式(12)和(13)模型的数值计算结果，计算中取模型参数b=0.125且c=±0.9,±0.6,±0.3下，cu,bu和c,b同步取完全相同的值，其余计算参数D0，u0，l，t0，c1，c0，Δt和Δx同以上多项式模式中参数的取值。从图4看出模型参数的变化对浓度分布形态的影响较小，对于本例，当b,bu一定时，c,cu的增大会导致浓度分布峰值位置滞后，浓度峰值增加。c,cu一定时，b,bu在一定范围内的变化对溶质浓度分布的影响很小。

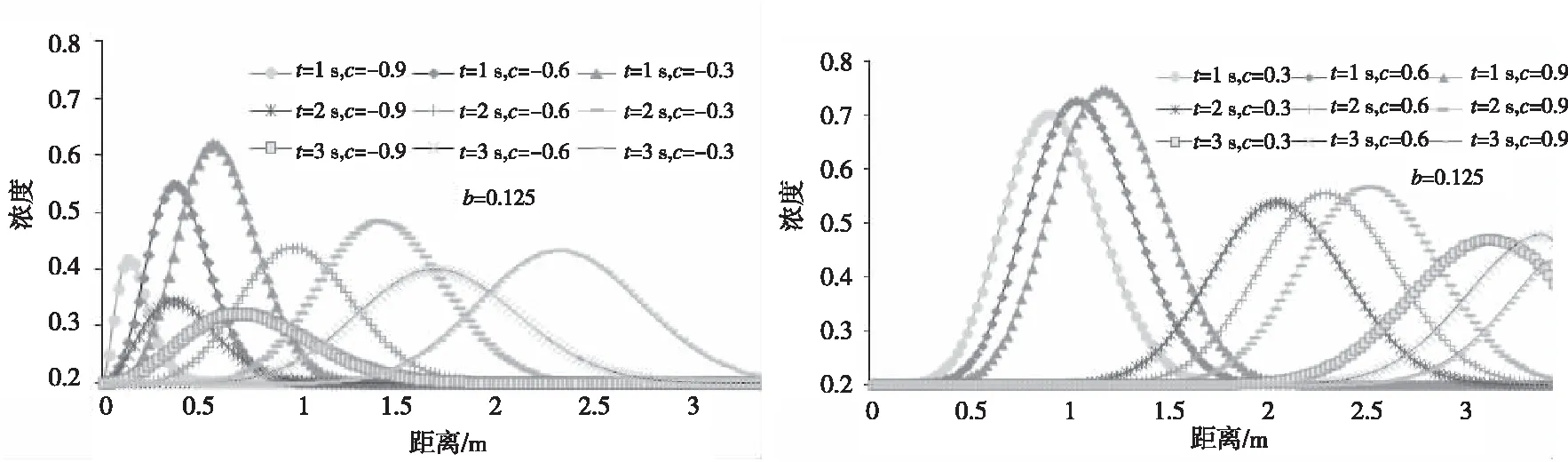
图4 指数模式溶质参数的一维溶质运移浓度分布及比较

4 结论

本文采用显式时间差分格式计算变溶质运移参数模型一维水流溶质运移过程，计算结果通过解析解进行验证，并和试验结果进行对比分析，说明算法可靠，显式法列式简单，更适于复杂模型计算[1]；模型越复杂，本法的计算效率越高。本文首次进行了变溶质运移参数模型溶质运移问题的数值计算，并建立不同的溶质运移参数模型，对该模型进行了参数分析。提出的系列算法和处理技巧可以应用到溶质注入水流后，变溶质运移参数模型的溶质迁移规律研究，通过建立不同模式下溶质运移参数模型，从而实现复杂条件下溶质运移过程的预测和模拟。