U型能量桩与混凝土桩抗震性能对比分析*

2021-06-16 07:20黄会杰郑永辉

西安工业大学学报 2021年2期

赵敏，黄会杰，郑永辉

(西安工业大学建筑工程学院，西安 710021)

能量桩技术，是基于桩基基础和传统地埋管地源热泵系统发展起来的，通过在桩基中埋设U型管或W型管，实现桩体与土体冷热交换，获取低温位的地热能，从而减少对传统化石能源的消耗，既有实现潜层地热能冷热交换功能,又有满足支持上部建筑荷载功能。德国的法兰克福主塔美茵塔、奥地利某康复中心与我国南京朗诗国际街区及世博园的世博轴都曾使用这一技术，但总体而言能量桩技术还处在前期研究阶段且国内外建筑实际应用并不普遍。文献[1]研究能量桩桩体位移在多次温度循环下的影响，其结果显示经过每次冷热循环后能量桩桩体发生沉降且随着冷热循环次数的增加沉降不断加大，制冷工作时荷载对桩顶产生影响更大。文献[2]研究W型、螺旋型与U型等不同埋管形式下能量桩的热力学特性，施加热荷载时桩体埋设方式为W型的能量桩热效应最为突出，同时其水平方向的土压力和能量桩桩端阻力变化最大，在施加冷荷载时桩体发生明显沉降。文献[3-5]进行现场试验，结果显示施加不同温度荷载引起的桩体热胀冷缩直接影响桩土相对位移，使得能量桩的侧阻力、负摩阻力和轴力分布等与常规桩有明显区别，由于现场试验条件较难以控制、复杂程度高和试验代价较大等，许多学者采用模型试验与数值模拟分析相结合的方法研究能量桩的工作特性及影响因素。文献[6]对PCC能量桩循环温度作用下热力学特性进行模型试验，研究得出能量桩的热循环(夏季模式)比冷循环(冬季模式)情况下换热效率高，冷热循环都将改变桩顶位移值且产生塑性变形。文献[7]通过加热响应试验研究能量桩的换热性能，现场试验表明：能量桩桩体较大时采用沿桩壁均匀铺设U型换热管，管长越长换热效率越高。桩体在加热过程中会引起桩身侧摩阻力变化，温度荷载导致部分侧摩阻力发生反向。目前在工程实际应用中怎样才能使能量桩具有更高的换热效率与能量桩在长期冷热循环换热过程中能否满足桩基沉降要求一直是当前研究的热点。然而能量桩在地震荷载作用下是否满足抗震要求，且对能量桩抗震性方面的研究当前鲜有涉足。为此，本文以U型埋设方式能量桩为研究对象，对能量桩在桩土非热交换情况(春秋季非工作状态)下的抗震性能进行研究，采用ABAQUS软件建立能量桩模型，分析普通混凝土桩与U型能量桩在El波、兰州波和人工波作用下的抗震性能，以期在实际应用过程中为能量桩设计提供参考。

1 工程背景

本模型以西安市某小区为工程背景，抗震设防烈度为8度，设计基本地震加速度值为0.20g，按设计地震分组为第一组。建筑场地类别为Ⅱ类，本场地设计特征周期为0.35 s。场地内基础以下各土层的材料参数见表1。

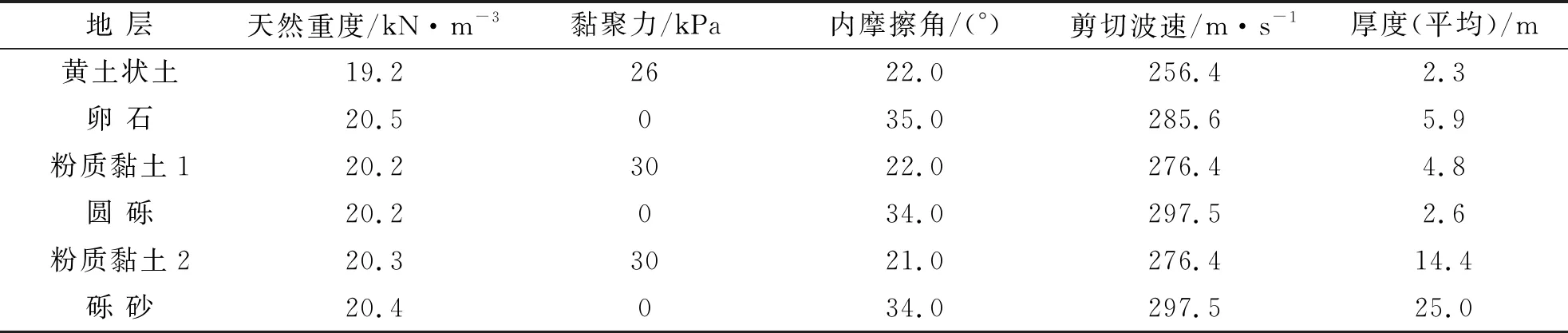
表1 土层参数

模型选择承台为4 m×4 m×2 m，并假定能量桩与承台一体，根据地质勘察报告选取30 m长，桩径600 mm，土体按10 m×10 m×50 m进行建模，U型管长29 m，U型管管径25 mm，径距500 mm。

2 抗震性分析

2.1 黏弹性边界可靠性分析

岩土工程数值模拟分析中，地应力平衡过程是求解研究土体初始地应力场的过程。地应力平衡所求解出的初始地应力场还原出土体的实际情况。J.H.Atkinson和G.Sallfors将地基土在动、静荷载作用下土的应变分为三类:≥10-2为大应变；10-5～10-2为小应变；≤10-5为极小应变。

实际工程测试结果表明，建筑物基坑、基础与隧道周围土体应控制在小应变范围内(10-4～10-3)。图1为地应力平衡后的应力，图2为地应力平衡后的位移，从中可以发现土体移动的数量级在10-4m级，相对整体模型小很多，土体不会发生较大变形，能够满足实际工程要求。

图1 地应力平衡后的应力

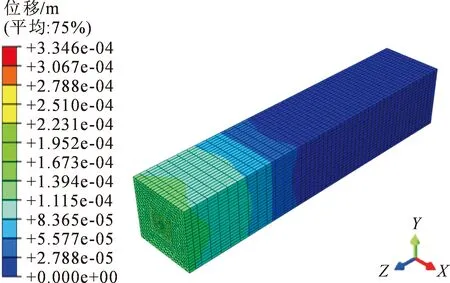
图2 地应力平衡后的位移

在工程抗震设计中，常用的人工边界有弹性边界、无限元和黏弹性边界等。黏弹性边界可以模拟散射波向无限域的传播和实现人工边界处介质的弹性恢复等特点，在人工边界节点的法向和切向设置并联弹簧和阻尼元件操作上更为便捷，因此采用该方法。并在进行地震作用分析前，对此处黏弹性边界进行测试，确定其可靠性。

验证等效节点荷载的模型尺寸为6 m×6 m×50 m，网格尺寸为1 m，介质的弹性模量为24 MPa，泊松比为0.2，密度为1 000 kg·m-3。

(1)

式中：E为弹性模量；μ为泊松比；ρ为质量密度；Vs为土的压缩波波速。压缩波速度为163.3 m·s-1。单位脉冲压缩波在模型底部垂直向上输入，压缩波的位移函数表达式为

(2)

式中：u(t)为位移；t为时间；f为频率。入射压缩波位移函数如图3所示，黏弹性边界和等效节点荷载图如图4～5所示，Z轴正方向为压缩波入射方向。图6为计算结果与理论对比，由波动理论可知，自由表面绝对位移的理论解为考虑行波效应延迟后放大2倍的入射位移时程。采用压缩位移波理论计算压缩波到达模型顶部时的土体最大竖向位移。表明黏弹性边界能够较好的对土体的地震波响应进行模拟。

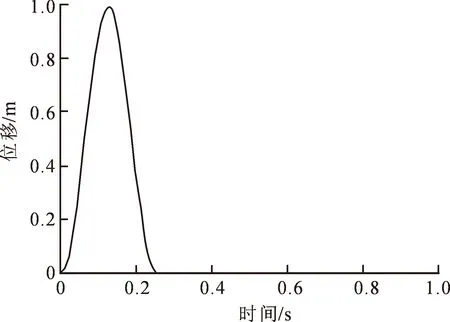
图3 入射压缩波

图4 黏弹性边界

图5 等效节点荷载图

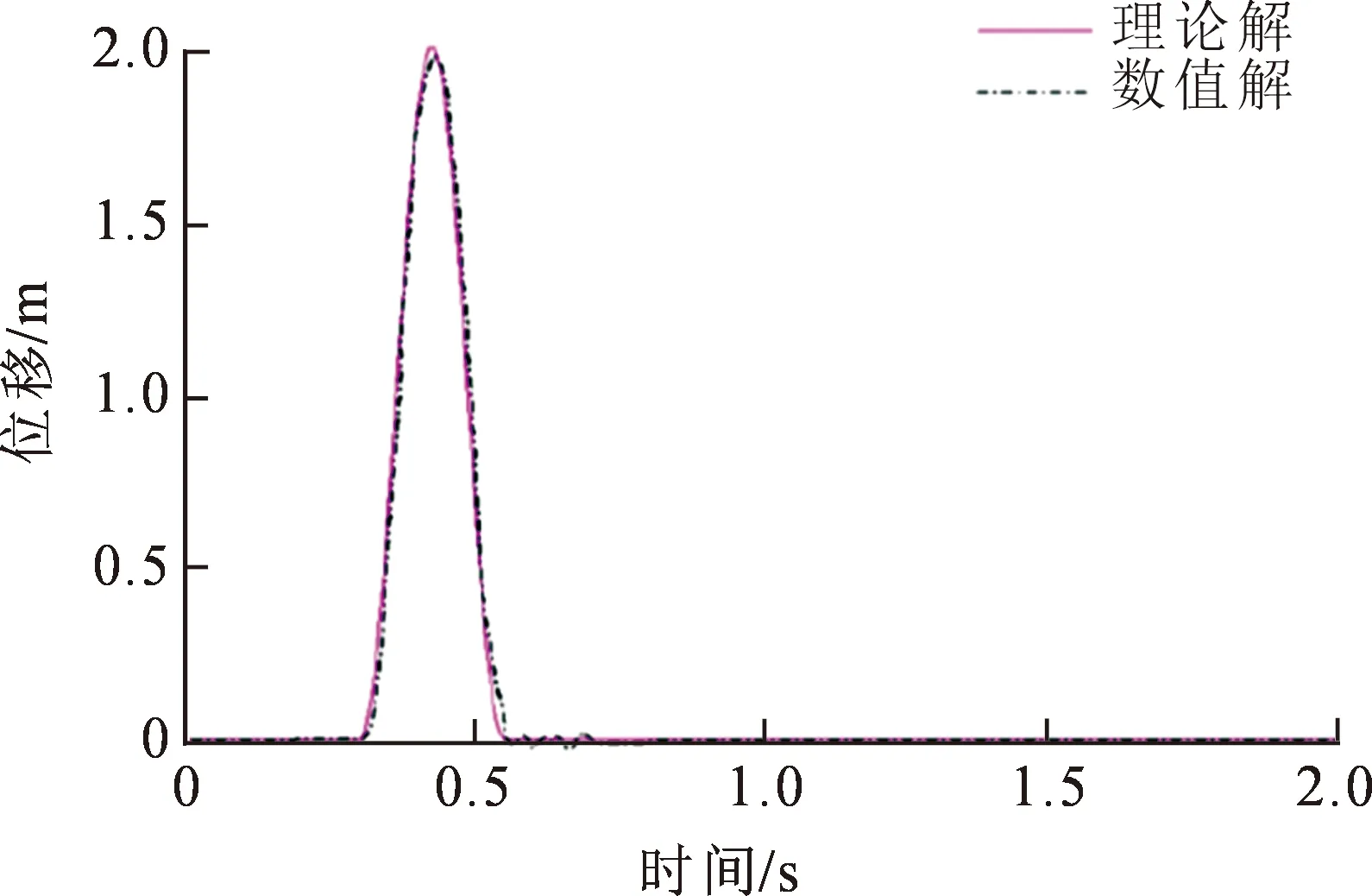
图6 计算结果与理论对比

2.2 地震响应分析

土-结构相互作用中的基岩地震动一般有3种选取方法：① 地震危险性生成工程场址法；② 地面地震动记录反演法；③ 使用地面地震动法。

综合考虑场地的设防烈度和震中距等因素，使用SHAKE91程序来反演基岩波，计算理想半无限空间的水平均匀成层土在竖向传播的剪切波作用下的响应。利用等效线性化方法对土体的非线性性质进行频域分析。

对于重要和不规则的建筑物通常采用时程法进行分析，应按设计地震分组与建筑场地类别选用不低于两组实际地震记录和一条人工模拟的加速度时程曲线。选取2条实际地震动及1条人工合成地震动，选用的地震动加速度时程曲线如图7所示。

图7 地震波加速度时程曲线

地震作用下能量桩与普通桩地震响应对比以El波为主进行分析，仅从加速度、位移、剪力和轴力4个方面进行具体分析。

2.2.1 对能量桩与普通桩地震作用下加速度时程分析

截取加速度时程进行分析，其中包含了桩体承台顶部和桩底加速度时程的最大和最小加速度，从图8～9可看出,在相同地质条件下，能量桩与普通桩的加速度是不一样的。

图8 能量桩加速度时程

由表2可看出，在El波地震荷载作用下，X、Y方向上承台顶部和桩底处普通桩的加速度均大于能量桩的加速度，这是因为能量桩相较于普通混凝土桩自重减小的缘故。

表2 地震响应加速度分析

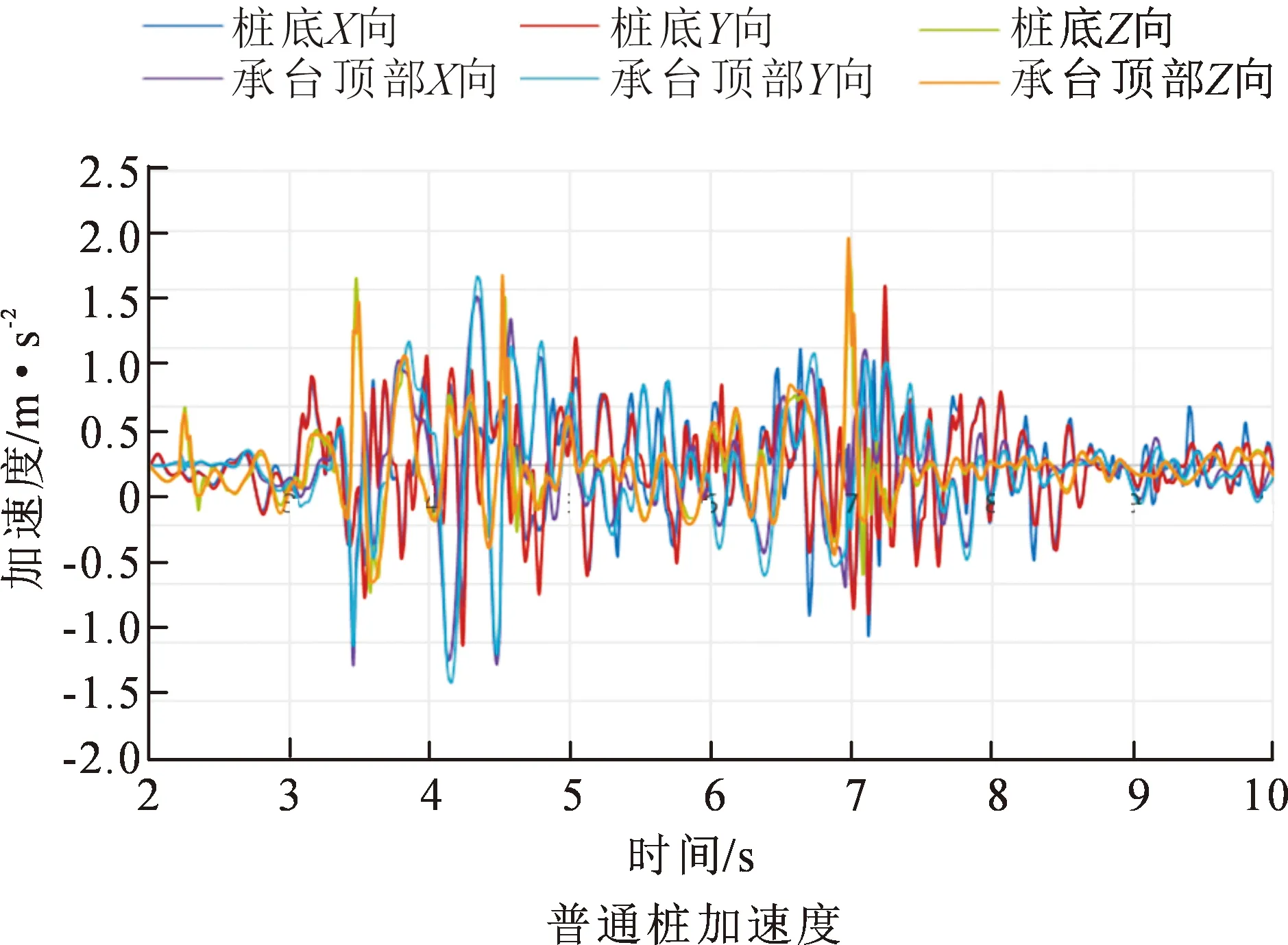
图9 普通桩加速度时程

2.2.2 能量桩与普通桩地震作用下位移分析

对能量桩和普通桩施加El波地震荷载，选取承台顶部和桩底底部作为桩体相对位移的参考点，图10和图11是能量桩与普通桩的相对位移时程，可以看出El波地震荷载作用下能量桩与普通桩在相同地质条件下X、Y方向的位移在时间约为5 s与7 s 时都有明显的突变，并且在这两点处位移值达到一定数值。在5 s时能量桩产生了最大的Y向负位移，其最大值约为0.057 453 2 m。同时普通桩产生了最大的X向负位移，其最大值为0.056 265 4 m。由此可以看出地震波对普通桩和能量桩的加强激励一致。地震响应位移分析见表3。

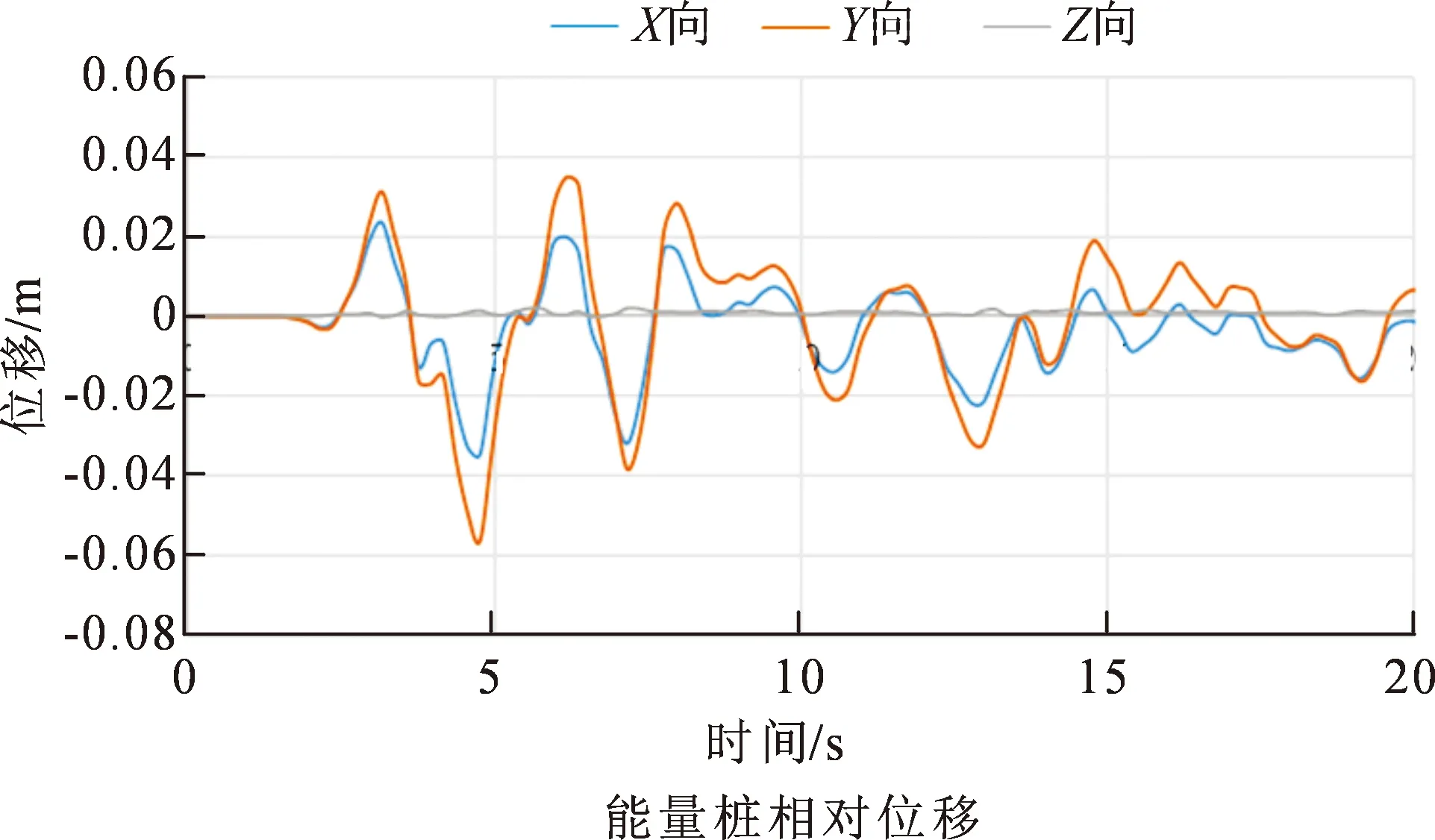
图10 能量桩相对位移时程

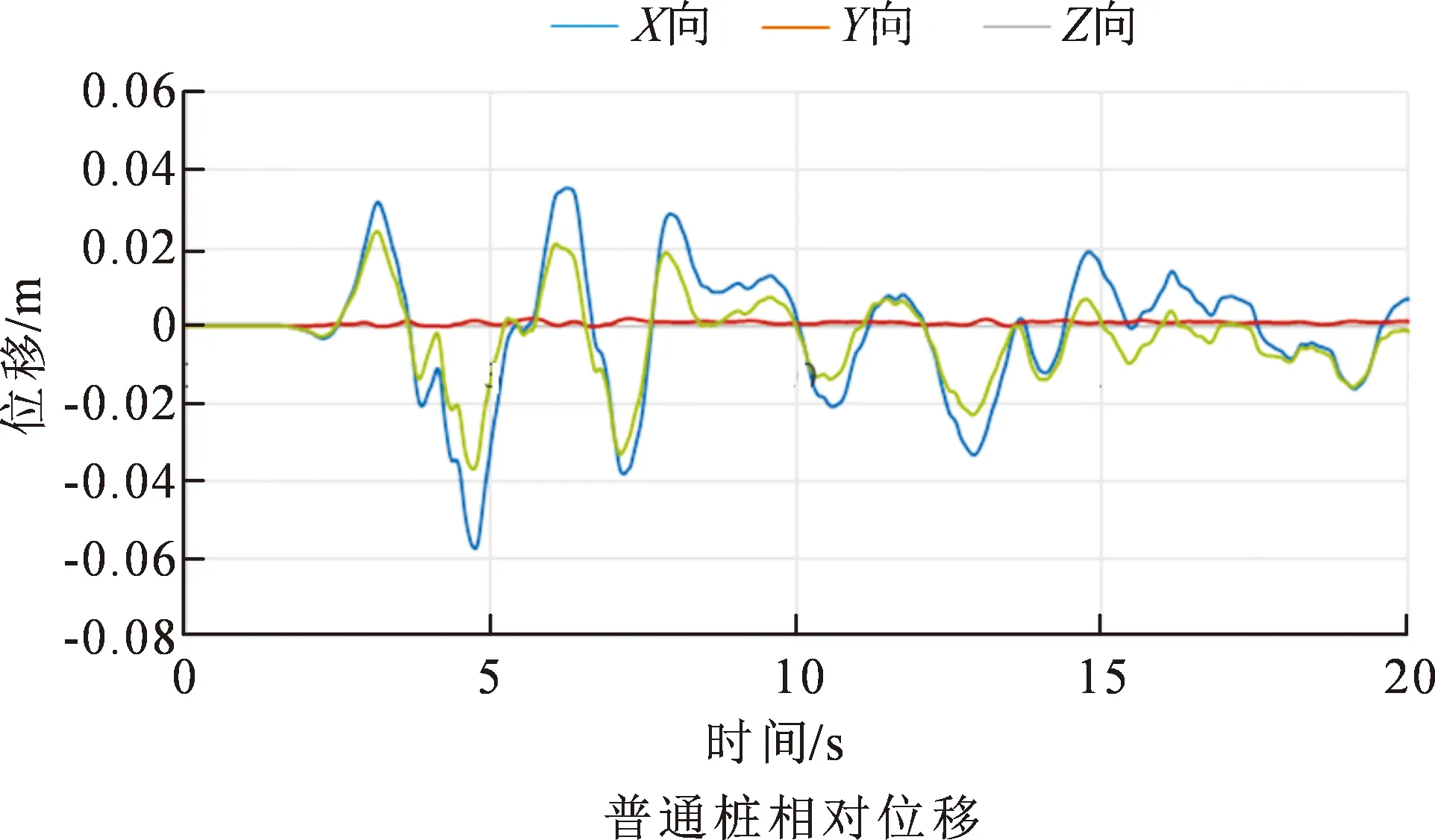
图11 普通桩相对位移时程

表3 地震响应位移分析

由表3可知，在E1波作用下,X方向上普通桩承台顶部和桩底之间最大相对位移为0.037 040 8 m，能量桩最大相对位移为0.034 731 2 m，相对于普通桩，能量桩的位移值在X方向上减少6.24%；在Y方向上普通桩承台顶部和桩底之间最大相对位移为0.057 453 2 m，能量桩最大相对位移为0.056 265 4 m，相对于普通桩，能量桩的位移值在Y方向上减少2.07%；在Z方向上普通桩承台顶部和桩底之间最大相对位移为0.002 155 9 m，能量桩最大相对位移为0.002 014 9 m，相对于普通桩，能量桩的位移值在Z方向减少6.54%；可见能量桩对普通桩而言有一定位移差，且能量桩在X方向和Y方向上的位移值均小于普通混凝土桩，与能量桩在X方向和Y方向上的加速度值均小于普通混凝土桩相一致，一般情况而言桩体破坏常常因为水平剪力过大导致，由此可以表明能量桩抗震性能优于普通桩。

2.2.3 能量桩与普通桩地震作用下剪力分析

在地震中地震波会对桩基产生剪应力，较大的剪应力常常会导致桩基出现剪切弯曲变形，故此要分析桩的水平剪力，见表4。在X方向上能量桩承台顶部的剪力比普通桩减小，能量桩桩底部的剪力比普通桩减小；在Y方向能量桩承台顶部的剪力比普通桩减小，能量桩桩底部的剪力比普通桩增加。

表4 地震响应剪力分析

2.2.4 能量桩与普通桩地震作用下轴力分析

在地震中地震波会对桩基产生轴应力，较大的轴应力常常会导致桩基出现较大沉降，故此要分析桩的轴力，见表5。普通桩承台顶部的轴力比能量桩小，普通桩桩底最大轴力比能量桩大。普通桩桩底轴力大于能量桩桩底轴力是由于能量桩桩体里面放置U型导管而导致桩体自身重量减少原因。对同一根桩而言，能量桩和普通桩桩底轴力均大于承台顶部轴力这是由于桩底承受了桩本身荷载。

表5 地震响应轴力分析

3 结论

采用El波、兰州波以及人工波对在非热交换条件下U型能量桩与普通混凝土桩的地震响应结果进行分析，得到结论为

1) 在设防地震条件下，能量桩地震响应后的位移相较于普通桩，在X方向上减小，在Y方向上减小，在Z方向上减小。

2) 能量桩承台顶部、桩底部X方向上的加速度幅值相较于普通桩均减小；能量桩承台顶部、桩底部Y方向上的加速度幅值相较于普通桩均减小。

3) 通过与普通桩的对比发现，能量桩的整体呈现出柔性特性，且抗震性能U型能量桩优于普通混凝土桩，在春秋两季即非热交换条件下能量桩满足抗震要求。