一种改进的混沌扩频序列性能研究

马玉峰 王洋

摘  要：混沌现象是非线性动态系统中出现的类随机过程，所产生的混沌序列因其码组丰富、抗干扰、抗截获能力强等特点，常作为跳频中的扩频码使用。本文对原有混沌扩频序列的量化方法进行改进，通过对迭代数值进行门限判决等方法，有效的减少了大量的初始值判决及复杂量化的过程。通过对改进后的Logistic混沌序列随机特性的验证及仿真，结果表明该序列具备良好的扩频特性。

关键词：混沌  扩频序列  自相关  游程

中图分类：TN914                              文献标识码：A                  文章編号：1674-098X（2021）01（a）-0102-03

Abstract： Chaos phenomenon that comes from nonlinear dynamic systems is a random process appearing， the generated chaotic sequence is often used as a spreading code in frequency hopping， because of its rich code group， strong anti-interference， and anti-interception ability. In the paper， the quantization method of chaotic spread spectrum sequence with threshold judgment on the iterative value was proposed， it could effectively reduce a large number of initial value judgments and complex quantization processes. Through the verification and simulation of the random characteristics of the improved Logistic chaotic sequence， the results show that the sequence has good spread spectrum characteristics.

Key Words： Chaos; Spread spectrum sequence; Autocorrelation; Runs

在扩频通信系统中，扩频运算是通过随机序列来实现的，性能良好的伪随机序列将直接影响扩频系统的抗干扰、抗多径衰落等能力。目前常用的伪随机序列有m序列、Gold码、M序列、Walsh码序列等，虽然它们都具备良好的自相关和互相关性，但受限于数目较少、复杂程度较低、抗截获能力较差等诸多缺点，已不能满足现代化通信系统的需要[1]。混沌系统由非线性方程构成，所产生的混沌序列具有良好的随机性、非周期性，同时满足现代通信系统对大量码组的需要，其统计特性与白噪声基本一致，因此具备较强的抗干扰、抗截获的特性[2-3]。常用的混沌序列有Logistic序列、Chebyshev序列及Kent序列等[4]，本文主要对Logistic-Map混沌序列传统的量化方法进行改进，并验证其特性。

1  混沌扩频序列

混沌系统可划分为以微分方程描述的时间连续系统和以状态方程描述的时间离散系统。时间连续系统用于实现保密通信，时间离散系统多用于产生大量的扩频序列。目前Logistic-Map混沌序列被广泛应用于扩频系统中，其映射方程为[5]：

当方程中3.56994≤k≤4时，系统工作在混沌状态，满足遍历性。处于混沌状态下所产生的混沌序列的相关特性如下[6]：

（1）自相关函数如下：

（2）任选两个初始值和，时间差为，互相关函数如下：

通过相关特性分析可知，当序列的长度时，Logistic-Map序列具有良好的伪随机特性，可作为扩频码用于扩频系统，但由于混沌序列所产生的序列码无法直接做为扩频码使用，需要对其进行量化及二进制转换。

现假设，在某通信系统中有W个用户，即需要W个扩频码，每个扩频码长度为N，根据以上需求，采用传统的方式，需要选择W个相互独立的初始值进行W*N次迭代运算，然后对迭代结果进行门限判决;很多改进后的方法虽然减少了初始值的数量，但同时增加了对迭代结果量化的过程，其复杂程度取决于扩频码的长度。

本文对原有的混沌序列数字量化过程进行改进，依据以上的假设，具体方法如下：

（1）根据系统对扩频码长度要求进行N次迭代，在公式（1）中选取初始值，获得混沌序列，，记为X;

（2）将X中数据小数点整体向右移动7位后取整数部分（移动位数需要考虑系统精确度），获得序列，记为Y;

（3）将Y中数据以b进行取余数，记为B，B为质数的集合。由b1得到序列，记为，进行W次取余数操作，获得序列集合，记为Z;

（4）门限判决通过对Z取期望得到，则有，最终获得W个长度为N的扩频序列码。

2  性能检验

伪随机序列具有理想序列的性质，应满足以下几点：（1）随机序列中“0”和“1”出现的次数近似相等;（2）随机序列中，长度为1的游程约占游程总数的1/2，长度为2的游程约占游程总数的1/4，长度为3的游程约占游程总数的1/8等等[7]。在同长度的游程中，“0”的游程和“1”的游程大致相等;（3）随机序列的自相关函数具有类似于白噪声自相关函数的性质。

本文通过对混沌伪随机序列分别进行单元测试、游程测试、自相关性和互相关性，来分析其性能，现选择20000比特进行如下测试：

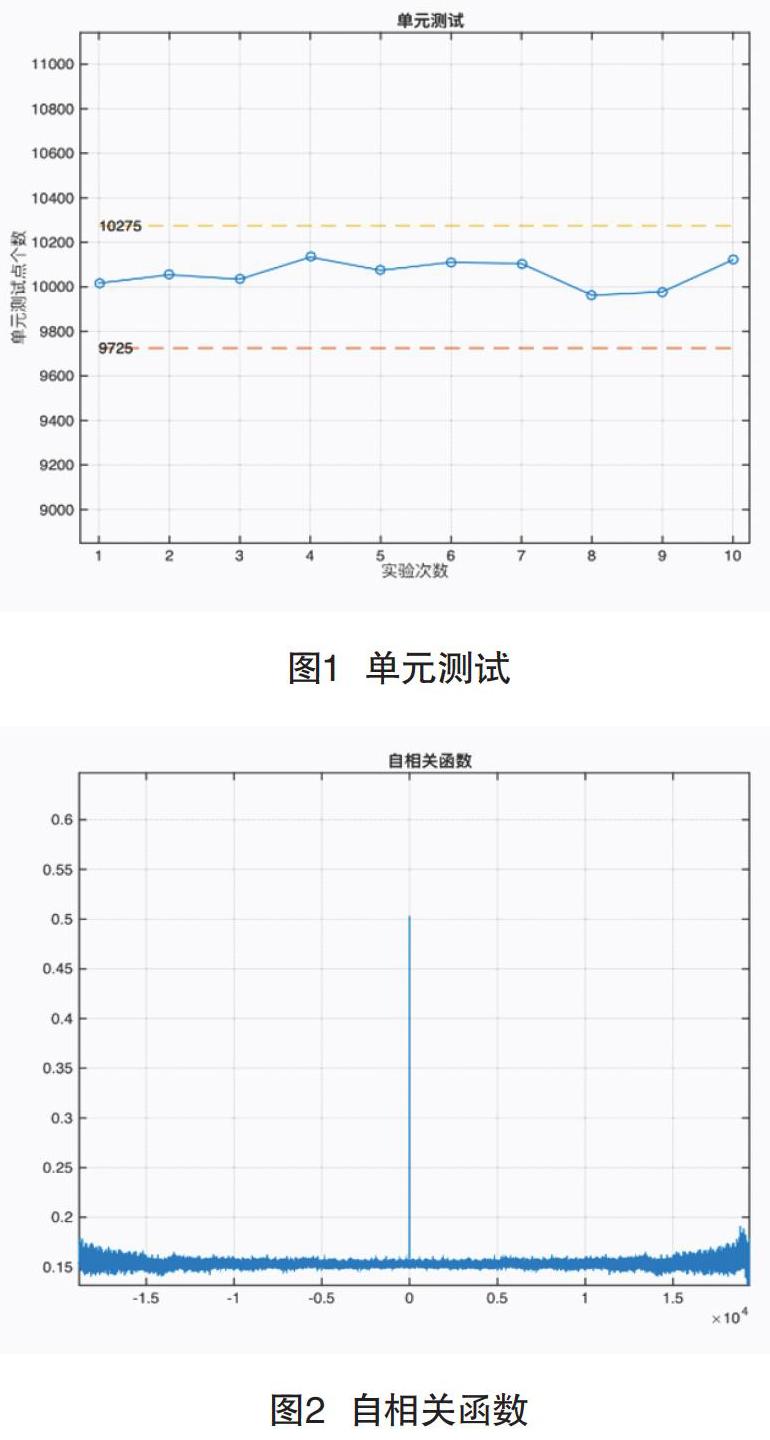
（1）单元测试：在20000比特中统计“1”或“0”的个数，任选10组不同的混沌序列，进行10次测试，其仿真结果如图1所示。通过仿真结果分析可知，其统计结果在9725～10275之间，表明本系统所产生的混沌序列通过单元测试。

（2）游程测试：在20000比特长度中，分别记录下“1”或“0”连续的个数，若游程长度“1”或“0”满足表1，则通过测试。表2为任选10组混沌序列的测试结果，可以看出，本系统所产生的混沌序列通过游程测试。

（3）自相关性及互相关性：任選两个不同的质数，分别获得两个混沌序列的自相关性和互相关性函数曲线，如图2、图3所示。可以看出，其自相关函数的相关峰尖锐，互相关数值几乎在0轴附近，说明此方法所生成的混沌序列具有良好的相关性能。

3  结语

本文对原有混沌扩频序列的量化方法进行改进，通过选择不同质数，有效的减少了大量的初始值判决及复杂量化的过程，通过对改进后的混沌序列进行仿真测试，结果表明改进后的序列具有较好的性能，满足伪随机序列的要求。

参考文献

[1] 张彦平，陆锐敏.一种改进的混沌扩频序列优选算法[J].计算机工程，2016，42（3）：121-124.

[2] 于一丁，王永川，王长龙.基于多值量化的混沌扩频序列及其性能分析[J]. 微型机与应用，2017，36（6）：58-61.

[3] 王小康.混合混沌扩频序列的研究及性能分析[D]. 西安：西安电子科技大学，2019.

[4] 田明浩，徐晓丹，刘芳，等.基于扩频的复合混沌优选序列生成方法[J].沈阳理工大学学报，2018，37（5）：1-6.

[5] 张怡，费恒敏，赵恒斌，等.混沌序列相关特性研究及在扩频通信中的应用[J].火力与指挥控制，2011，36（11）：18-24.

[6] 贾亚娟，王亚亚.改进型Logistic混沌序列发生器的设计与实现[J].机械与电子，2019，7（4）：22-27.

[7] 郭思毅.基于混沌调制的声呐收发系统设计[D].太原：中北大学，2020.