滚动体和滚道误差对滚珠丝杠副载荷分布的影响研究
曾石蔷,周长光,王 凯,欧 屹,韩 军
(南京理工大学机械工程学院,江苏 南京 210094)
随着近些年来国家装备制造业振兴计划和数控机床发展战略的实施,具有高速度、高精度的高性能滚珠丝杠副已成为滚珠丝杠副的必然发展趋势。滚珠丝杠副的载荷分布,对滚珠丝杠副的传动精度、传动效率及滚珠丝杠副服役寿命有着重大影响[1-2]。因此,在对滚珠丝杠副进行优化设计、提高滚珠丝杠副定位精度时,精确地计算滚珠丝杠副载荷分布是必不可少的。
滚珠丝杠副的静态载荷分布直接决定了滚珠丝杠副静态承载能力和精度,常作为分析滚珠丝杠副某些动态特性的基础,在滚珠丝杠副载荷分布中显得尤其重要。然而,典型的滚珠丝杠副系统很难直接测量一定轴向载荷下滚珠的受力。一些学者将丝杠、螺母视为二维板,试图通过实验方法测量滚珠丝杠副的静态载荷分布[3],这种简化方式很难精确地测量实际的滚珠和滚道力及变形关系。鉴于实验测量滚珠丝杠副载荷分布的难度很大,大多数学者采用仿真的方法来预测载荷分布。但现有滚珠丝杠副载荷分布模型的建立[4-5]都忽略了滚道误差,对滚动体误差的研究也存在很大不足。赵国平[6]、张佐营[7]和甄妮[8]等以轴向载荷均匀分布在每个受载滚珠上为前提进行数学建模,分别提出了滚珠丝杠副的滚珠与滚道接触力及接触变形的计算方法,但最后得到的数学计算模型均没有考虑到不同位置的丝杠螺母单元变形量变化对滚珠与滚道接触变形的影响;Mei等[9]在研究滚珠误差对载荷分布影响时,认为滚珠与滚道接触角对载荷分布影响可以忽略,在建立载荷分布计算模型时将接触角视为常量45°,这与滚珠与滚道实际接触状态不符;Xu等[10]对文献[9]提出的滚珠误差模型进行改进,考虑到滚珠与滚道接触角的变化, 提出先将大滚珠尺寸压缩成最小滚珠尺寸,再采用文献[9]的模型进行载荷分布计算,这种处理方式没有考虑到赫兹力和赫兹变形的非线性关系。
针对现有关于滚珠丝杠副静态载荷分布研究的不足,本文提出了考虑滚动体误差、滚道误差的载荷分布计算模型,探究了不同加工精度下滚珠对滚珠丝杠副载荷分布的影响,并结合国内厂家实际加工丝杠过程中产生的滚道误差,分析滚道误差对滚珠丝杠副载荷分布的影响,验证了滚动体和滚道加工精度对产品性能的重要性。
1 影响滚珠丝杠副载荷分布的误差来源
影响滚珠丝杠副载荷分布的因素主要有滚动体的几何误差和滚道的几何误差。
1.1 滚动体的几何误差对载荷分布的影响
实际滚动体生产中,滚珠实际值和标准值之间会存在偏差。当滚珠尺寸不存在偏差时,可认为滚珠与滚道初始接触角为45°;当滚珠误差为正时,滚珠与滚道的初始接触角将减小;同理当滚珠误差为负时,滚珠与滚道之间接触角变大。接触角的变化直接改变了滚珠与滚道接触点的位置,也改变了滚珠与滚道接触力大小。
1.2 丝杠滚道加工误差对载荷分布的影响
国内丝杠生产厂家在进行丝杠滚道加工时,大多采用先车削再磨削的方法。每次磨削前用金刚石刀具对砂轮进行修整,然后再进行砂轮定位。上述丝杠滚道加工方式产生的滚道误差主要分为以下3种。
1)砂轮几何误差导致的滚道左右圆弧半径误差。为了得到理想的砂轮廓形,需要进行多次打磨完成砂轮廓形的修正,每次打磨后利用投影仪将砂轮廓形放大,通过与标准廓形进行对比得到误差。这种打磨方式能够极大降低砂轮廓形的误差,但是人为因素影响较大,实际上砂轮左右圆弧半径仍存在误差。如图1所示,忽略砂轮在单次磨削时的磨损量,滚道半径误差大小和砂轮廓形误差将保持一致。当丝杠滚道半径存在误差时,滚珠与滚道接触点发生改变,导致滚珠丝杠副载荷分布发生改变。

图1 丝杠滚道半径大小误差图
2)滚道圆弧中心位置的波动误差。由于砂轮定位精度和各加工元件刚度的影响,砂轮中心在多次磨削过程中并不能完全重合,砂轮中心在丝杠轴向产生的波动导致丝杠滚道圆弧中心在轴向产生波动,如图2所示。当滚道中心位置发生偏移时,部分滚珠因为受到螺母的挤压导致变形量和接触力变大。
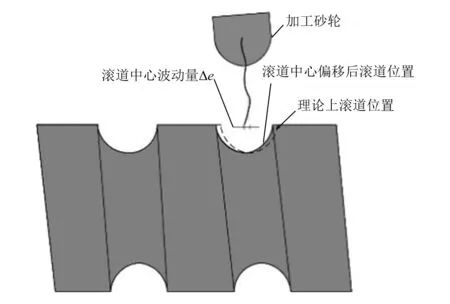
图2 丝杠圆弧滚道中心波动误差图
3)丝杠热伸长产生的导程误差。丝杠滚道切削和磨削加工过程中,加工丝杠会产生较大的热变形,不同的冷却方式可以在一定程度上减小热变形的影响,但不能完全消除热变形。在热变形影响下,实际加工得到的丝杠导程会小于理论值,导程的减小导致滚珠被挤压,滚珠与滚道的接触变形及接触力变大。
2 考虑滚动体和滚道误差的载荷分布计算模型
2.1 考虑滚道误差的滚珠丝杠副载荷分布计算模型


图3 单螺母滚珠与滚道接触状态
设第i个滚珠和滚道法向接触力大小为Qi,丝杠轴向力的平衡方程为:
(1)
式中:α为螺旋升角;αi为第i个滚珠和滚道的接触角;M为滚珠个数。
由图3可得丝杠和螺母第i个单元受到轴向力为:
(2)
根据赫兹接触理论,滚珠和滚道法向接触力Qi与接触变形δi关系可表示为:
(3)
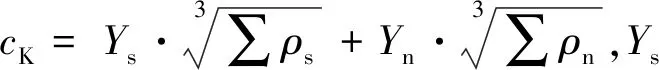
丝杠和螺母单元轴向变形量Δsi和Δni计算公式为:
(4)
(5)
式中:ΔL为丝杠螺母单元长度;Es和En分别为丝杠和螺母的弹性模量;As和An分别为丝杠和螺母的横截面积。


图4 滚珠球心、丝杠螺母滚道曲率中心在 承受轴向载荷后的法向平面几何位置变化图
由图4可得滚珠和滚道之间的弹性变形量δi为:
(6)
Abi=(fs+fn-1)Dbsinα0+δbi
(7)
Ani=(fs+fn-1)Dbcosα0
(8)
式中:fs,fn为丝杠、螺母滚道半径的适应度;Db为滚珠直径;α0为未受载时滚珠与滚道的初始接触角,在不考虑滚珠、滚道误差时α0的值为45°;δbi为受载后丝杠滚道曲率中心在b轴方向位置变动量。
受载后滚珠与滚道接触角可表示为:
(9)
当滚道存在半径误差Δr时滚珠与滚道初始接触角α0为:
(10)
因为滚珠和螺母受到压力,丝杠受到拉力,且三者均发生弹性变形,根据滚珠和丝杠螺母的接触关系,可以将图1中滚珠和滚道的接触关系简化成如图5所示,得到滚珠丝杠副第i单元丝杠、螺母、滚珠三者在轴向载荷下的变形协调关系为:

图5 滚珠与滚道接触关系简化模型
(11)

在不考虑螺母加工误差的情况下,当与滚珠i处丝杠滚道中心偏移量为Δe时(丝杠滚道中心向左偏移时Δe为正,向右偏移时为负),滚珠和丝杠螺母接触关系如图6所示。根据图6易得滚珠丝杠副第i及第(i+1)单元丝杠、螺母、滚珠三者在轴向载荷下变形协调关系为:
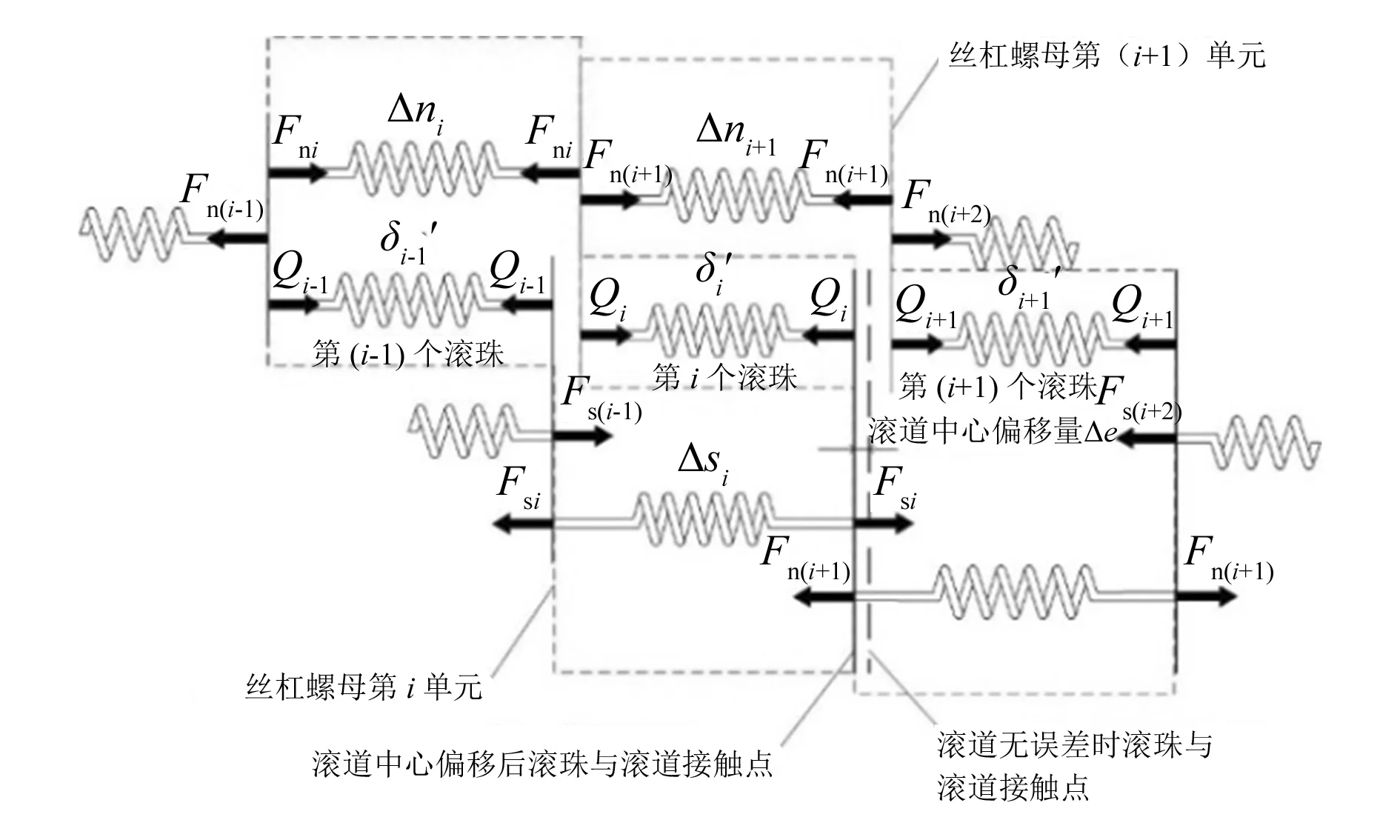
图6 滚珠丝杠副第i与(i+1) 单元滚珠和丝杠、螺母接触简化图
(12)
(13)
同理,当丝杠在加工过程中由于热变形导致导程减小Δp时,滚珠丝杠副第i及第(i+1)单元丝
杠、螺母、滚珠三者在轴向载荷下变形协调关系为:
(14)
(15)
将式(12)~式(15)合并可得滚道加工误差影响下滚珠丝杠副第i及第(i+1)单元丝杠、螺母、滚珠三者在轴向载荷下变形协调关系为:
(16)
(17)
将式(2)~式(5)代入式(16)、(17)可得:
(18)
(19)
其中:
2.2 考虑滚动体尺寸误差的载荷分布计算模型
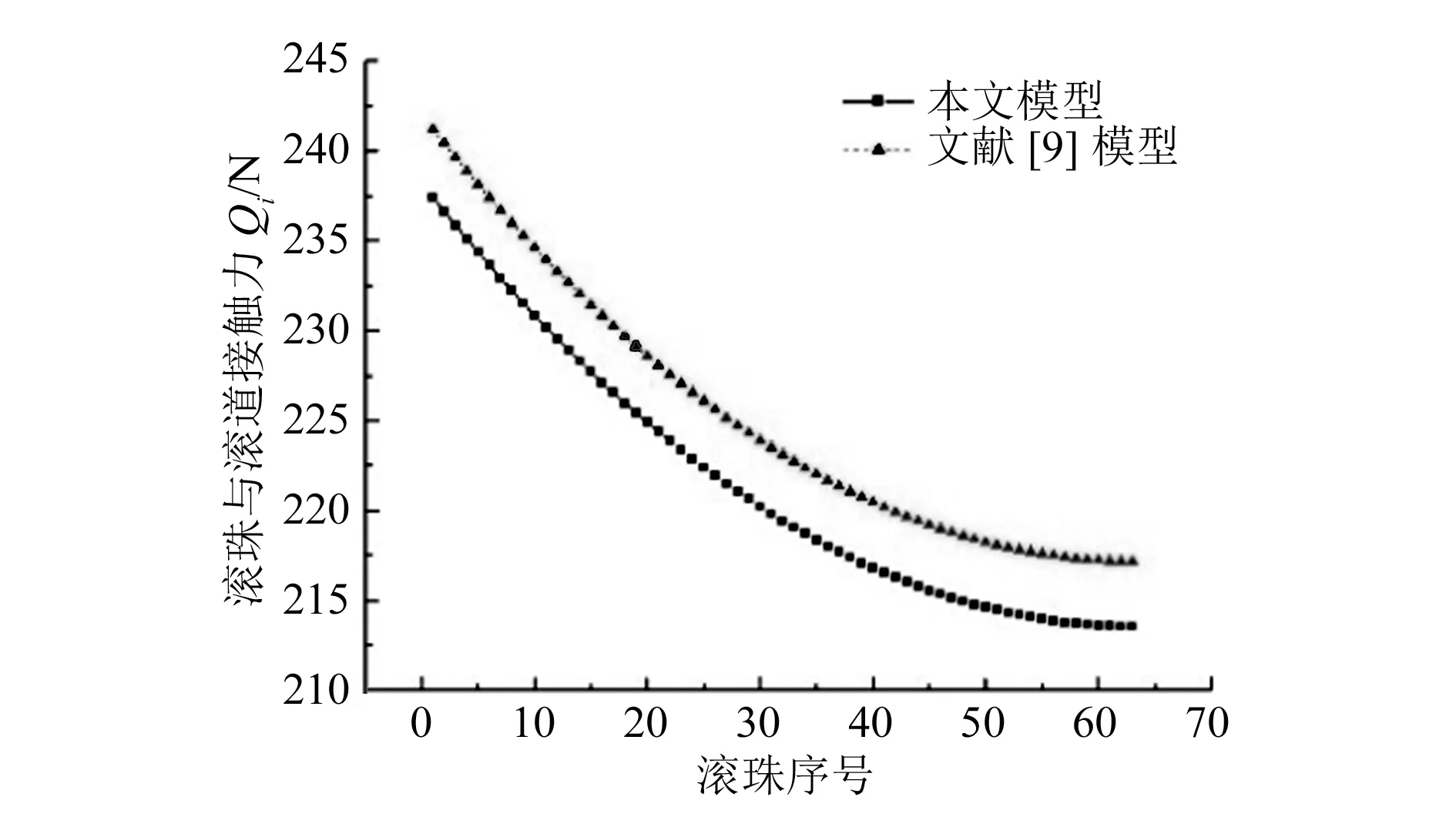
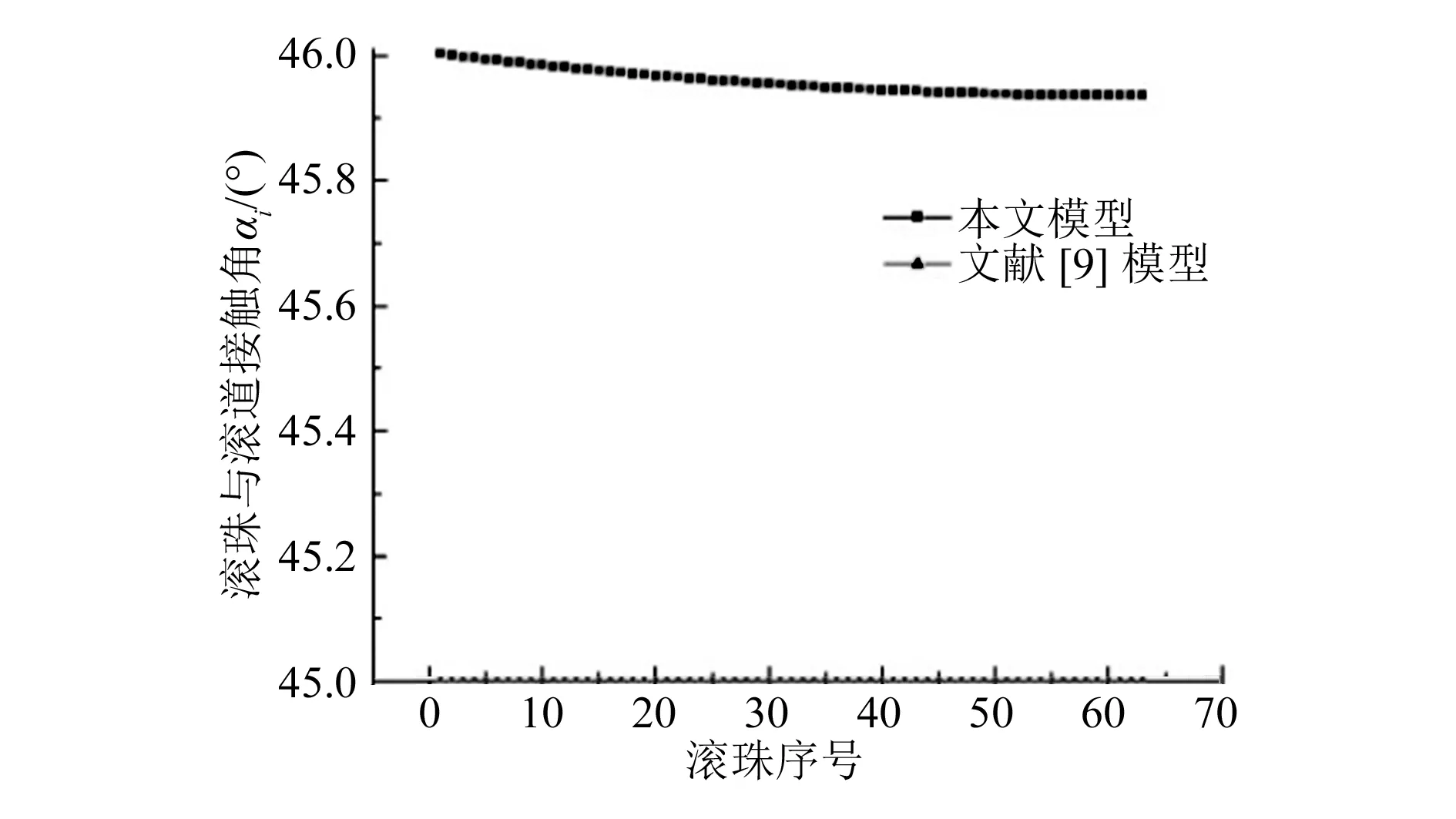
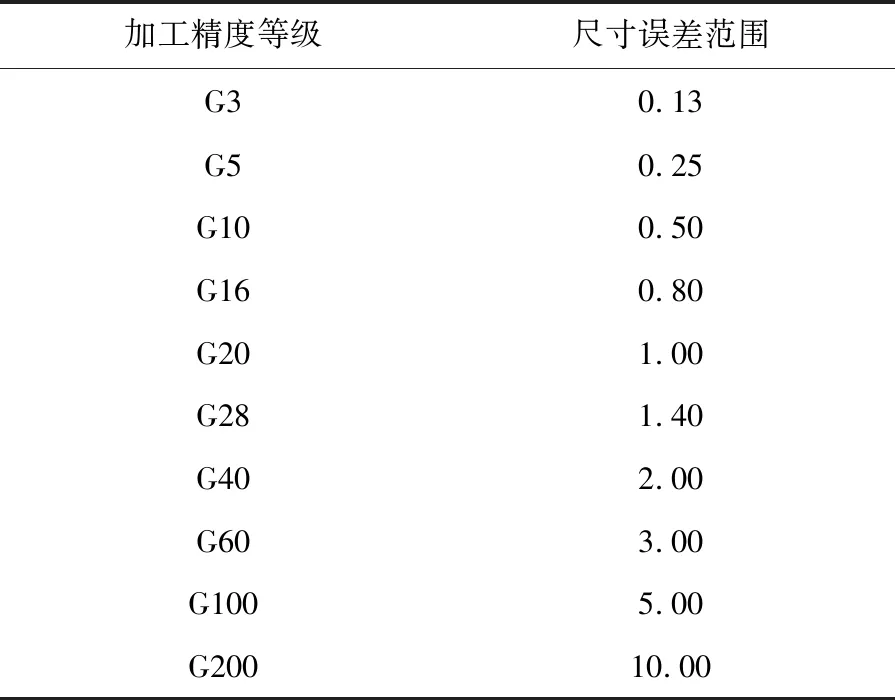
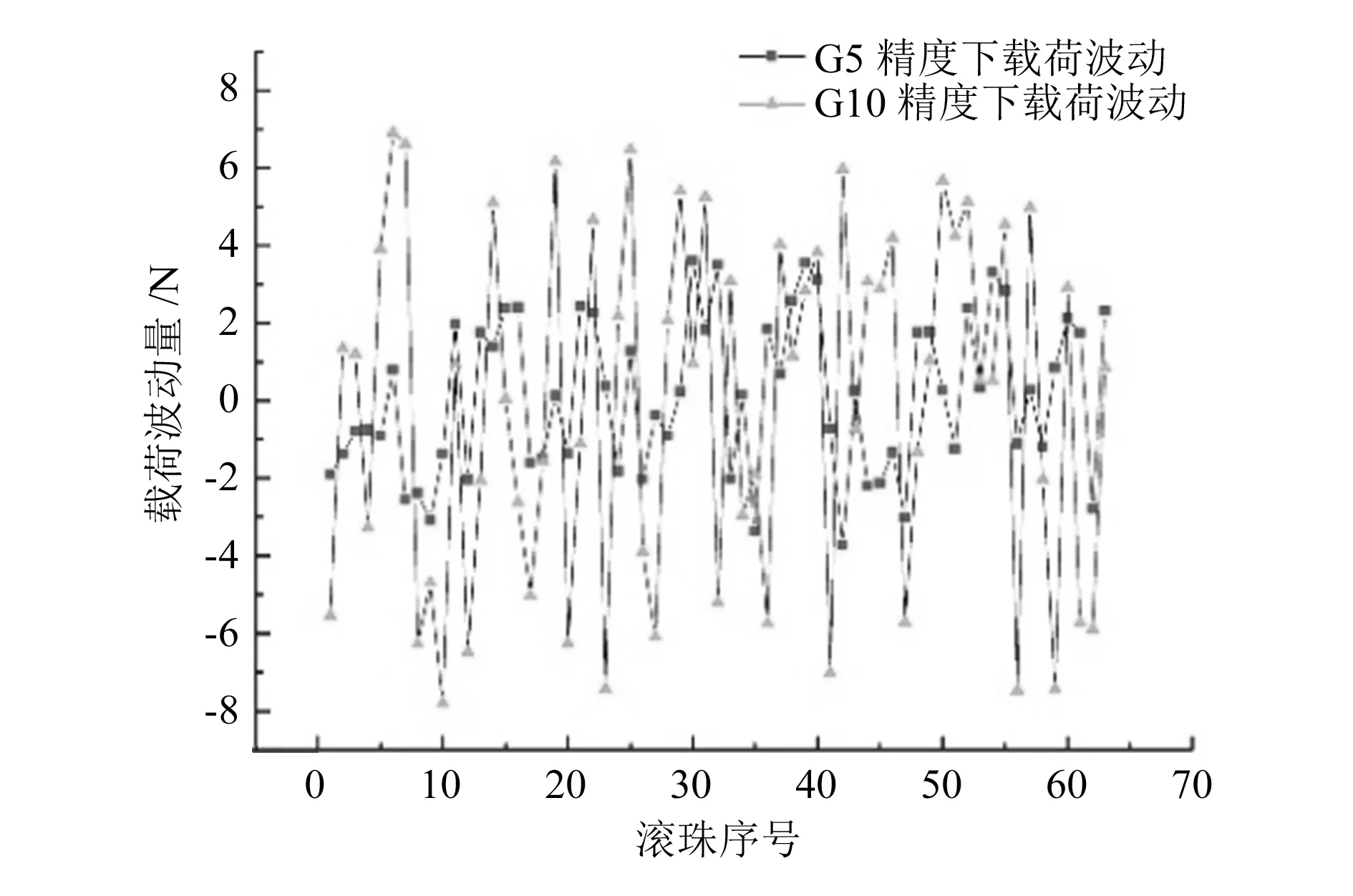
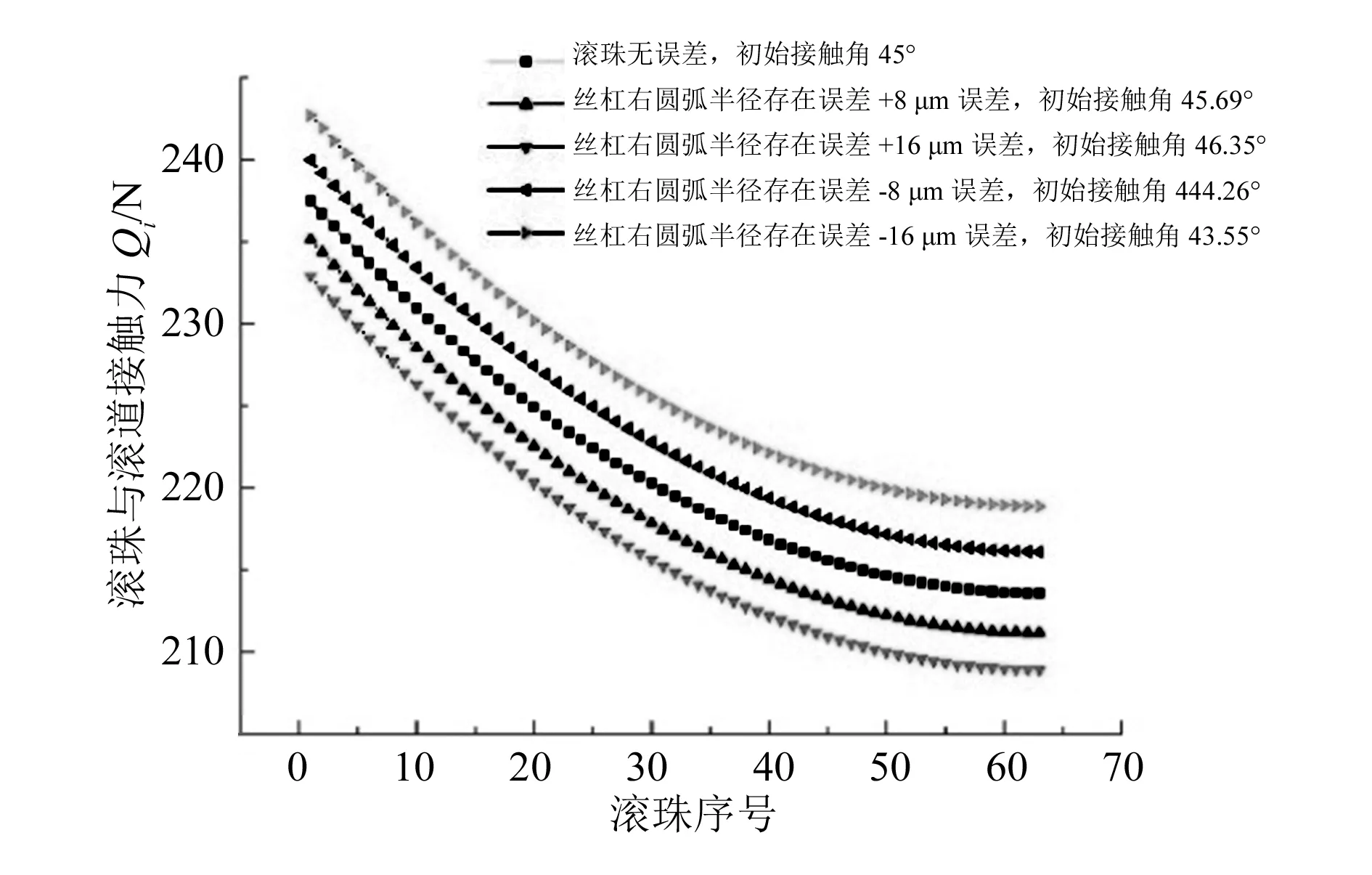
设第i个滚珠的尺寸偏差为Ti,Ti为正代表滚珠尺寸存在正误差,Ti为负代表滚珠尺寸存在负误差。假设滚珠丝杠副有3个不同大小的滚珠和滚道接触产生接触变形,如图7所示,其中Ti<0 图7 滚珠与滚道接触简化图 根据滚珠大小关系,将非最大滚珠j(j=i-1,i)放大成最大滚珠大小(即第(i+1)个滚珠大小),滚珠j在轴向载荷作用下产生的变形过程分为两个阶段:当滚珠与滚道法向接触变形量小于(Ti+1-Tj)时,滚珠与滚道之间未产生接触力;当滚珠与滚道法向接触变形量大于等于(Ti+1-Tj)时,滚珠和滚道发生弹性变形,产生接触力。 丝杠、螺母的第i、(i+1)单元与第(i-1)、i 和(i+1)个滚珠形成的变形协调关系为: (20) (21) 将式(2)~式(5)代入式(20)、(21)中得: (22) (23) 滚珠和滚道初始接触角α0为: (24) 当第i个球很小时,第i个滚珠在轴向载荷下可能并未发生接触变形,滚珠和滚道接触变形量δi=0,此时可将第(i-1)和第(i+1)个滚珠及其之间的丝杠螺母部分构成第i个受力单元。第i单元滚珠及丝杠长度为: (25) 第i单元轴向变形协调方程为: (26) 判断在一定轴向载荷下滚珠的受载情况,可以采用如下方法: 1)将滚珠按照尺寸从小到大排列,得到Tk1 2)从最小的第k1(j=1)个滚珠开始,依次判断kj是否满足不等式: (27) 直到找到满足不等式的最小kj值; 3) 滚珠kj,kj+1,…,kM受载,滚珠k1,k2,…,kj-1不受载。 结合公式(1)、(3)、(6)~(11)、(20)~(24),可以得到4M个非线性等式,分别对应滚珠与滚道接触力Qi、滚珠与滚道法向接触变形量δi、不同位置处丝杠滚道曲率中心在b轴方向位置变动量δbi、滚珠与滚道接触角αi(i=1,2,…,M)共4M个未知数,因此可以通过MATLAB数值迭代的方法求得滚珠与滚道接触力、接触角、变形量的大小。 近年来,结构紧凑、刚性高(承载滚珠数多)的滚珠丝杠副应用越来越广泛,因此本文的仿真分析选用汉江机床厂生产的HJG-S系列4010型内循环滚珠丝杠副进行分析,其参数见表1。 表1 滚珠丝杠副参数表 所选滚珠丝杠副额定动载荷为30 kN,设滚珠丝杠副承受轴向载荷为10 kN,利用MATLAB求解载荷分布模型方程,可以得到滚珠丝杠副的载荷分布及不同位置处滚珠与滚道接触角。在不考虑滚动体与滚道误差的情况下,对文献[9]提出的模型和本文建立的模型分别进行求解,得到的载荷分布对比结果如图8所示,不同位置滚珠与滚道接触角对比结果如图9所示。 图8 不同模型的滚珠丝杠副载荷分布对比 从图8、图9可以看出,在不考虑误差时,本文提出的模型和文献[9]提出的模型得到的载荷分布趋势一致,由于本文提出的模型考虑了接触角变化,计算得到的每个滚珠与滚道接触力比文献[9]提出的模型减小3.6~3.8 N,即减小了1.6%~1.7%。这也说明滚珠与滚道接触角对载荷分布有一定的影响,忽略滚珠与滚道在承受轴向载荷后接触角变化得到的载荷分布是存在误差的。 图9 不同模型的滚珠与滚道接触角对比 1)滚动体精度对载荷分布的影响。 根据《机械设计手册》[12],滚珠加工精度有10个等级,不同加工精度等级下滚珠直径误差见表2。其中G10精度的滚珠半径误差在 0.250 μm以内随机变化,G5精度的滚珠半径误差在 0.125 μm以内随机变化。利用MATLAB随机生成不同加工精度下滚珠半径误差值,在G5、G10精度下得到滚珠随机误差曲线如图10所示。当滚珠丝杠副承受的轴向载荷为10 kN时,滚珠丝杠副载荷分布如图11所示。由图10和11可知,不考虑滚珠加工误差时滚珠与滚道接触力曲线可以看成是不同精度下滚珠与滚道接触力曲线的中心线。G10精度下滚珠误差波动大于G5精度下滚珠误差,对应载荷分布曲线波动也大于G5精度下的载荷分布波动。这也说明滚珠加工精度越高,滚珠丝杠副的载荷分布越平稳。 图11 不同精度滚珠载荷分布 表2 不同加工精度滚珠对应尺寸误差 单位:μm 滚珠丝杠副摩擦力矩主要受单个滚珠与滚道接触处摩擦系数和接触载荷大小的影响,在滚珠丝杠副润滑良好的情况下,滚珠丝杠副摩擦力矩由接触载荷大小决定[13]。由图10和11可知,滚珠误差导致滚珠与滚道接触载荷产生波动,滚珠精度越高,滚珠与滚道接触载荷波动越小。将不同精度滚珠承受载荷和理想滚珠承受载荷的差作为波动值来表征载荷分布波动情况,得到载荷波动图如图12所示。从图12可以发现,当滚珠精度从G10提高到G5时,载荷波动值扩大一倍。因此,为了减小摩擦力矩波动,需要选用精度较高的滚珠。 图10 不同精度下滚珠几何误差分布 图12 不同精度滚珠载荷波动 2)单个滚珠精度对载荷分布的影响。 设滚珠丝杠副承受的轴向载荷为10 kN,除滚珠17加工精度较低外,其余滚珠加工精度等级均为G3。当滚珠17加工精度等级为G40时,分别取G40加工精度等级内最大滚珠误差±1 μm作为滚珠17的误差,得到滚珠丝杠副载荷分布如图13所示。由图13可知,当滚珠17加工精度较低时,该滚珠和滚道接触力会产生突变。若滚珠存在正误差,滚珠与滚道接触力会突然增加;若滚珠存在负误差,滚珠与滚道接触力会突然减小。增大或减小的接触力由其余滚珠承担,相邻滚珠并不会产生接触力的突变。 图13 滚珠17加工精度等级为G40时 滚珠丝杠副载荷分布 滚珠的负误差几乎不改变滚珠与滚道的最大接触力与接触变形,滚珠的正误差会导致滚珠与滚道的接触力和接触变形增大,而滚珠和滚道最大接触力与接触变形代表了滚珠丝杠副的刚度、摩擦力矩大小[9],所以接下来只考虑滚珠正误差对滚珠丝杠副载荷分布的影响。分别假设滚珠17加工精度为G60、G100、G200,取加工精度等级内最大正误差作为滚珠17的误差,得到滚珠丝杠副载荷分布如图14所示,从图14可以得到:采用同一尺寸不同精度等级滚珠进行混合搭配时,精度较低的滚珠与滚道接触载荷会发生突变,在轴向载荷为10 kN、滚珠17加工精度等级为G200时,滚珠17与滚道的接触力从226.6 N变成388.8 N,即接触力为原来的1.71倍,接触力的成倍增加导致滚珠丝杠副的刚度迅速变差,滚珠与滚道之间摩擦力和摩擦力矩突然增加,滚珠与滚道磨损增大,滚珠丝杠副寿命降低。这说明单个滚珠加工精度对滚珠丝杠副性能有着很大的影响,为了得到稳定的滚珠丝杠副性能,需要控制每个滚珠的加工精度。 图14 单个低精度滚珠对滚珠丝杠副载荷分布影响 1)左右圆弧半径误差对载荷分布的影响。 国内厂家在丝杠生产过程中,更加关注丝杠的验收指标,如丝杠行程、误差等参数,忽略了左右圆弧滚道的加工精度,使丝杠左右圆弧的加工精度得不到保证。以国内T2级滚珠丝杠副为例,在保证滚珠丝杠副的行程误差满足出厂要求后,滚道左右圆弧实际半径值与设计半径值之间滚道误差仍可能存在数十微米的误差。假设滚道右圆弧分别存在+8 μm、+16 μm、-8 μm、-16 μm的半径误差,在轴向载荷10 kN下,滚珠丝杠副载荷分布如图15所示。由图15可知,滚道半径误差直接影响滚珠与滚道的初始接触角大小。当滚道右圆弧增大时,滚珠与滚道初始接触角增大,滚珠丝杠副载荷分布曲线向下偏移,滚珠与滚道的法向接触力整体减小;当滚道右圆弧减小时,滚珠与滚道初始接触角增大,滚珠丝杠副载荷分布曲线向上偏移,滚珠与滚道的法向接触力整体增大。当滚道半径误差为8 μm时,每个滚珠与滚道的接触力均发生0.9%~1.1%的变化。滚道半径误差变化量越大,滚珠与滚道的法向接触力变化量越大。因此,为了得到准确的滚珠丝杠副载荷分布,需要考虑滚道左右圆弧的半径误差。 图15 不同滚道半径误差下滚珠丝杠副载荷分布 2)滚道中心位置波动误差对载荷分布的影响。 表3 各公差等级下2π 弧度内行程误差变动量 单位:μm 图16 丝杠不同公差等级下滚珠丝杠副载荷分布 图17 丝杠不同公差等级下滚珠丝杠副载荷波动 3)热伸长产生的导程误差对载荷分布的影响。 以丝杠生产常用材料轴承钢为例,轴承钢温度每升高1 ℃,每1 m轴承钢热伸长量为12 μm。本文选用丝杠的导程为10 mm,实际滚道磨削过程中丝杠温度升高为4~10 ℃,通过数学计算得到丝杠导程误差为0.48 ~1.20 μm。考虑丝杠热伸长后得到的滚珠丝杠副载荷分布曲线如图18所示。由图18可知,丝杠热伸长使滚珠丝杠副载荷分布曲线趋势从下降变成上升。产生这种现象的原因是丝杠热伸长使得丝杠导程小于螺母导程,导致滚珠被进一步挤压,随着滚珠序号的增大,丝杠和螺母滚道之间存在的偏移越来越大,滚珠和滚道挤压变形也越来越大,最终导致载荷分布呈现上升趋势。当加工温度升高4 ℃时,滚珠丝杠副载荷分布趋于平稳,当温度升高大于5 ℃时,载荷分布迅速变差,各位置滚珠承受载荷不均匀,滚珠丝杠副运动不平稳,定位精度变差。因此,可以认为适当的丝杠热变形能够对载荷分布起补偿作用,但是当丝杠热变形过大时,滚珠丝杠副载荷分布迅速变差,滚珠丝杠副性能降低。通过选择合理的冷却方式,调整丝杠磨削温升值,可以得到更稳定的载荷分布。 图18 热变形影响下滚珠丝杠副载荷分布 本文考虑到滚珠与滚道接触角变化和不同位置处丝杠螺母单元轴向变形量变化的影响,建立了轴向载荷下滚珠丝杠副载荷分布计算模型,并分析了滚动体误差、滚道误差对滚珠丝杠副载荷分布影响。根据仿真分析结果,可以得到结论: 1)在一定轴向载荷下,滚珠丝杠副中滚珠和滚道接触力大小并不相等,力作用点处第一颗滚珠受力最大,其余滚珠受力依次减小。 2)滚珠与滚道接触角的变化对载荷分布有一定影响,为了得到准确的滚珠丝杠副载荷分布,需要考虑滚珠与滚道接触角的变化。 3)滚珠加工精度直接影响滚珠与滚道接触力波动情况,通过控制滚珠加工精度等级,可以得到更加平稳的载荷分布,从而减小摩擦力矩波动及滚道磨损,增加滚珠丝杠副服役寿命。 4)滚珠丝杠副中滚珠与滚道接触力的最大值取决于加工精度最低的滚珠。当滚珠尺寸具有较大正误差时,该滚珠与滚道接触力迅速增大,滚珠丝杠副承载能力变差,刚度降低。因此,为了提高滚珠丝杠副的承载能力及刚度,需要控制每一个承载滚珠的加工精度。 5)丝杠的滚道加工误差对控制滚珠丝杠副的载荷分布非常重要。滚道半径误差使得滚珠丝杠副载荷分布曲线发生偏移,从本文仿真结果可知,轴向载荷为10 kN时,T2级滚珠丝杠副存在的滚道中心误差可导致单滚珠承受载荷变化量达1%;滚道中心偏移误差决定了滚珠丝杠副行程误差,当丝杠行程误差满足验收标准时,滚道中心位置产生的载荷波动误差大小可以忽略;适当的温升引起的导程误差能够对载荷波动起补偿作用,而当温升过大时,滚珠丝杠副载荷分布迅速变差,滚珠丝杠副性能降低。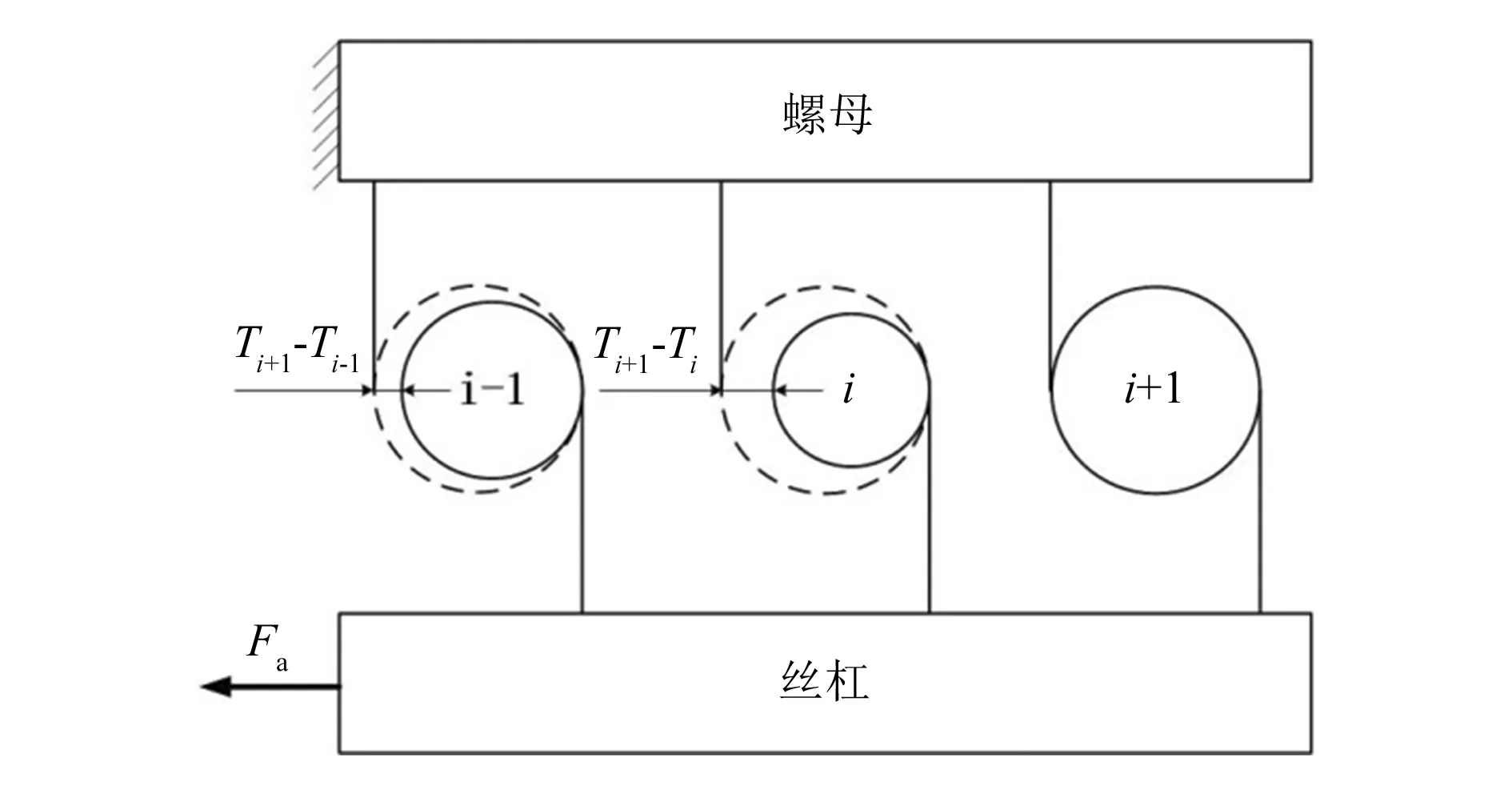
3 仿真分析

3.1 滚动体精度对载荷分布的影响




3.2 滚道误差对载荷分布的影响




4 结论

