基于平行四边形机构的天线举升装置设计

刘建坤，南江红，王光辉，翁艺航，黄佳雷

(上海航天电子技术研究所，上海 201109)

现代战争对地面雷达的机动性和环境适应性提出了更高的要求[1-2]。现代车载雷达通常处于两种状态——工作状态和运输状态。在工作状态时为了减小地物载波对雷达系统的影响，需要天线举升装置将雷达天线升至要求的高度，工作完成后降低天线的高度，使其处于运输状态，满足公路和铁路运输的要求。因此，需要设计一种天线举升装置实现雷达天线的升降，完成工作状态和运输状态的转换。目前雷达天线举升装置的机构形式主要有翻转式、升降筒式和多连杆式，以及上述方式中两种或多种形式的组合方式[3-4]。翻转式天线举升装置[5]其天线或天线座与载车底盘通过铰链连接，液压缸或电动缸推动天线翻转到指定角度；升降筒式天线举升装置采用多级套筒[6]依次嵌套的方式实现天线的升降；多连杆式天线举升装置[7-8]是通过多个平面连杆机构实现天线的升降。平行四边形机构具有良好的移植性和通用性，在雷达车上使用该机构可满足机动性好、越野能力强、架撤方便等要求。基于受力均布的考虑，将两套平行四边形机构布置于载车的两侧[9-10]，既能提高系统的稳定性，节省出的中部空间还可用于集中布置其他设备。

本文根据平行四边形机构的原理设计了一种基于平行四边形机构的天线举升装置。

1 举升装置技术指标

基于平行四边形机构设计的天线举升装置主要技术指标如下。

1)举升高度：≥1.5 m。

2)举升/撤收时间：≤3 min。

3)举升质量：>500 kg。

4)系统自重：<350 kg。

5)到位精度：X<3′，Y<3′。

6)八级风(20 m/s)载荷时最大位移量：<15 mm。

7)举升到位后能够可靠锁定与解锁。

设计天线举升装置时要充分考虑人机工程学，在满足功能技术指标的前提下，还要使其结构紧凑、美观、轻巧。

2 构型设计

平行四边形机构由基座、两个曲柄和连杆组成，两个曲柄与基座连接，连杆与两个曲柄连接。平行四边形机构的两个曲柄以相同的速度同向转动，连杆作平动。在进行天线举升装置设计时，将基座安装在载车底盘或专用的支撑框架上，在框架的两侧平行安装两套平行四边形机构，将机构的连杆设计成雷达天线的基座。平行四边形机构由电动缸驱动，电动缸具有结构紧凑、维护成本低、干净无污染等特点，电动缸一端连接曲柄，另一端连接底座框架。根据其功能和构型设计要求，天线举升装置的系统组成如图1所示，构型如图2所示。

图1 系统组成框图

图2 天线举升装置构型

底座框架与调平系统是天线举升装置的基础部件，承载了其他所有部件的质量，并保证了雷达系统的基础水平度要求。双平行四边形机构是实现天线举升和撤收的关键部件。电动缸与控制系统用于驱动双平行四边形机构的运动。位置检测装置主要检测平行四边形机构运动的位置，使雷达天线能够稳定快速地举升和撤收。锁定机构在雷达天线举升到位和撤收到位后锁定机构状态，保证其安全可靠地工作。

3 机构分析

天线举升装置的构型设计完成后，对机构进行运动特性和静力特性分析，为工程设计时零件形状设计、材料选择和强度校核提供依据。如图2所示，升降平台与曲柄1和曲柄2通过铰链连接，铰接位置分别是p1和p2，曲柄1和曲柄2互相平行，与基座通过铰链连接，铰接位置分别是p3和p5，电动缸伸出端与曲柄2通过铰链连接，铰接位置是p4，电动缸固定端与底座通过铰链连接，铰接位置是p6。平行四边形机构的自由度是1，通过电动缸的伸缩实现平行四边形机构的运动。曲柄1和曲柄2的长度分别为l1和l2，曲柄2与水平面的夹角为θ，以点p2为基准，则升降平台距离天线撤收状态时的高度h为：

h=l2sinθ

(1)

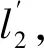
(2)

对式(2)求导可得：

(3)

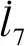
根据点的速度合成定理，电动缸绕p6点的转动角速度ω7为：

(4)

(5)

(6)

(7)

式中：α为曲柄的角加速度。

根据技术指标和运动特性分析可知，平行四边形机构的举升和撤收过程比较缓慢，因此只对该机构进行静力特性分析，主要分析天线基座在不同位置时机构在运动过程中对电动缸的输出力要求。由于曲柄相对于升降平台和雷达天线的质量很小，为简化计算，可以忽略曲柄自身的重力。

对天线基座进行受力分析，如图3所示，天线基座所受力主要是其自身与天线的重力之和G以及曲柄1、曲柄2的作用力F1和F2。曲柄1是二力杆，曲柄1对升降平台的作用力F1方向可知，平行于曲柄1且过p1点，将曲柄2对升降平台的作用力分解为水平方向的F2x和竖直方向的F2y。点p1和点p2的距离为l3，点p2到曲柄1的距离是l5，l3与水平面的夹角为δ1。

图3 天线基座受力图

基于天线基座受力的平衡，对p2点取矩得：

(8)

l5=l3·sin(θ+δ1)

(9)

式中：l3x为l3的水平分量。

曲柄1对升降平台的作用力F1为：

(10)

故有

(11)

(12)

对曲柄2进行受力分析。曲柄2对升降平台的作用力为F2，故曲柄2受到升降平台的反作用力大小与F2相等，另外曲柄2还受到电动缸的作用力F4，F4的方向平行于电动缸且过p4点，以及受底座的支反力F5，其受力示意图如图4所示。电动缸与曲柄2的夹角为β2，点p5到电动缸l7的距离为l6。

图4 曲柄2受力图

基于曲柄2受力的平衡，对p5点取矩得：

(13)

故电动缸的输出力为：

(14)

由式(14)可得电动缸的输出力和曲柄转动角度θ的关系，据此可知天线举升装置在举升的起始阶段对电动缸的输出力要求最大。因此，在电动缸选型时，当天线的质量确定后就可以根据式(14)确定电动缸的输出力。

4 天线举升装置设计

对平行四边形机构进行运动学分析和静力学分析后，天线举升装置的基本参数和运动关系已经确定，可以对机构零件进行详细的工程设计。根据以上分析和技术指标要求设计的天线举升装置如图5所示，主要包括底座、调平腿、平行四边形机构、电动缸、升降平台、翻倒锁定装置、起竖锁定装置、位置检测装置和控制系统。在升降平台的两侧对称位置分别布置了一个平行四边形机构，每个平行四边形机构分别由一个电动缸驱动，因此需要控制系统和位置检测装置共同保证电动缸伸缩的同步性，以避免两侧的平行四边形机构因不同步而产生内应力。

图5 天线举升装置

天线的到位精度主要由曲柄、底座框架和天线基座的加工和装配精度保证。天线举升和撤收时间主要由伺服控制系统保证。

图5所示为天线举升状态，在此状态时天线基座的上平面保持水平，曲柄保持竖直，通过机械限位和两侧曲柄上的起竖锁定机构保证天线举升装置成为一个具有良好稳定性的刚性体。举升时，撤收锁定机构解锁，电动缸伸长，升降平台升高，曲柄到达竖直状态时，升降平台到达最高位置，电动缸停止工作，举升锁定机构锁定，举升过程结束。举升过程如图6所示。撤收时，首先举升锁定机构解锁，然后电动缸开始收缩，曲柄开始绕支座翻转，升降平台随之下降，当曲柄处于水平状态时，升降平台处于最低位置，电动缸停止工作，撤收锁定机构锁定，撤收过程结束。

图6 举升过程

5 强度校核

对天线举升装置中重要的零部件进行强度校核。由静力分析可知，机构从撤收状态开始举升时电动缸输出力最大，此时曲柄2受力最大，因此对曲柄2进行强度校核。曲柄2的材料为Q235方钢管，材料的屈服极限σs为216～235 MPa。根据静力分析可知，在起竖起始状态时，电动缸推力F4最大。此时曲柄2受力如图7所示。

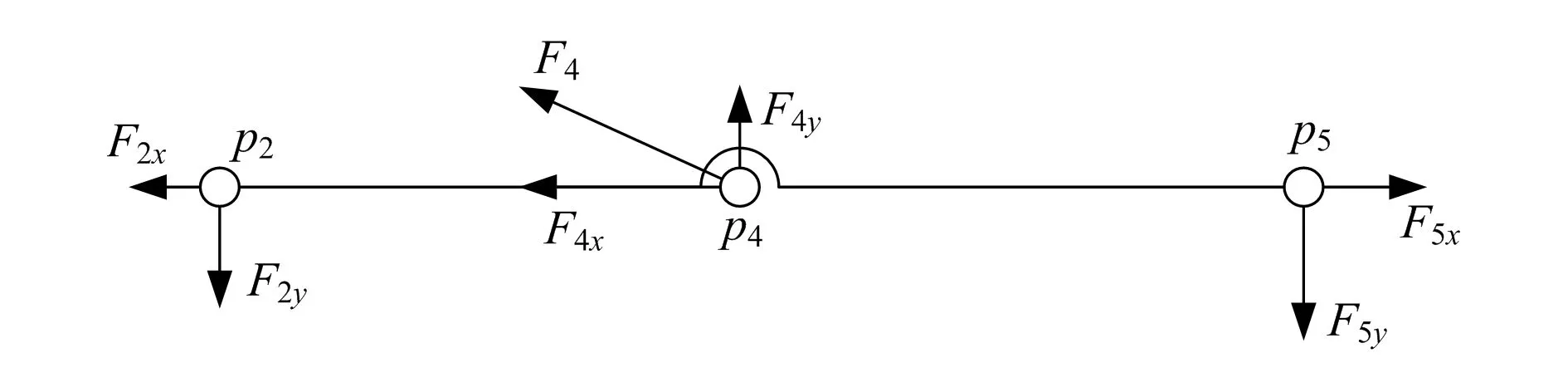
图7 曲柄2受力图

假设天线基座和天线的总质量为1 000 kg，由于平行四边形机构对称布置在升降平台的两侧，因此可以认为单侧的平行四边形机构受到的作用力为5 000 N。根据式(11)和式(12)可知，F2x=5.358×103N，F2y=5 000 N，方向如图7所示；根据式(14)，力F4水平和竖直方向的分解力为：F4x=F4cosβ2=2.85×104N ，F4y=F4sinβ2=7 835 N，方向如图7所示。基于曲柄2受力平衡计算支座对曲柄2的支反力：

F2x+F4x-F5x=0

(15)

F2y-F4y-F5y=0

(16)

由式(15)、(16)求得F5x=3.386×104N，F5y=2 835 N，方向如图7所示。

根据分析和计算可知曲柄会发生拉伸和弯曲组合变形。对p2p4段内的轴向力、剪力和弯矩进行分析计算，p2p4段受力如图8所示，图中lx表示p2p4段内任一截面到点p2的距离。

图8 对p2p4段受力分析

基于p2p4段受力平衡可知，p2p4段的轴向力为Fa24=F2x=5.358×103N，剪力为Fs24=F2y=5 000 N，弯矩为M24=F2ylx，最大值为3 080 N·m。轴向力、剪力和弯矩的方向如图8所示。

图9 对p4p5段受力分析

根据以上计算，曲柄2的危险截面(受力最大、最可能发生断裂的截面)在点p4的右侧。曲柄2是横截面为70 mm×70 mm、壁厚为5 mm的方钢管。轴向力引起的拉应力σ1为：

(17)

式中：A为方钢管横截面积，A=1 300 mm2。由弯矩引起的最大拉应力σ2为：

(18)

式中：Mmax为曲柄的最大弯矩；W为抗弯截面系数。根据材料力学中组合变形叠加原理，可得曲柄2的最大拉应力σ为：

σ=σ1+σ2=143.112 (MPa)

(19)

曲柄2的最大拉应力小于其屈服极限216～235 MPa，由此可知，曲柄2满足强度要求。

6 稳定性分析

稳定性分析[11]主要是对八级风载荷(20 m/s)下机构的抗风能力进行分析，以确定天线基座上的天线位移量是否小于15 mm。

天线举升装置处于工作状态时主要受到天线和其自身重力G以及侧向八级风载荷F的作用，天线举升装置处于图10所示状态时受到的风载荷最大，因此只计算此状态下风载荷对机构的稳定性影响。

图10 天线举升装置受风载荷

假设天线的高度为1 m，宽度为1.4 m，此时天线举升装置的迎风面积S为2.97 m2。

风载荷按公式(20)计算：

(20)

式中：C为空气阻力系数，一般取1；ρ为空气密度，kg/m3，取1.293 kg/m3；S为迎风面积，m2；v为风速，m/s。

计算得到八级风载荷作用下装置受到的总的风载荷F=768.04 N，方向垂直于装置的侧面。

为简化计算，假设风载荷的作用点位于天线的中心，天线中心的高度为h1=3.48 m，则风载荷产生的最大倾覆力矩M1为：

M1=F·h=2672.78 (N·m)

(21)

天线的质量为800 kg，举升装置的质量为340 kg，重力臂为b，则天线举升装置自身重力稳定力矩M2为：

M2=G·b=15 102.26 (N·m)

(22)

在八级风载荷作用下天线举升装置的稳定系数η为：

η=M1/M2=5.7

(23)

最小稳定系数一般取2.5，故在八级风载荷作用下天线举升装置工作稳定。

对天线举升装置在八级风载荷作用下进行仿真分析，为简化计算，将风载荷简化为集中力且只作用在天线基座上，大小为768.04 N，底座框架与地面固定连接。得到的仿真结果如图11所示。

图11 八级风载荷时机构变形量仿真结果

从图中可以看出，八级风载荷作用下机构的变形很小，最大变形只有0.247 mm，位于升降平台的上边缘，不会影响天线举升装置的稳定性。

7 结束语

本文设计了一种基于平行四边形机构的天线举升装置，通过对平行四边形机构的分析和优化设计，基于平行四边形机构的天线举升装置满足技术指标要求，并且具有刚度好、强度高、稳定性强，结构紧凑、外形美观的特点。在设计和分析过程中发现曲柄2受力比曲柄1大，因此在以后的设计中可以减小曲柄1的横截面积，进一步减轻自重。本文的研究成果可供以后的高机动雷达设计时参考。