改进收敛因子和变异策略的灰狼优化算法

林梅金，汪震宇

（佛山科学技术学院机电工程与自动化学院，广东佛山 528225）

受到灰狼捕猎行为的启发，Mirjalili 等人［1］提出了一种新的群智能优化算法—灰狼优化算法（GWO）。该算法具有易于实现、收敛速度快和寻优性能好的优点，已被广泛应用于数据缓存、生产调度和图像处理等领域［2］。然而在处理复杂优化问题时，GWO 仍存在收敛速度慢和容易陷入局部最优解的缺点。为了解决这些问题，学者们对GWO 算法做了很多改进［3-4］。

为了进一步提升GWO 算法的优化性能，本文提出了一种基于改进收敛因子和变异策略的新型灰狼优化算法。仿真结果表明，所提算法不仅能提高GWO 算法的收敛速度，而且能提升其寻优精度。

1 灰狼优化算法

在GWO 算法中，每只灰狼都代表着优化问题的一个潜在解，其中最优解、优解、次优解和候选解分别被称为α 狼、β 狼、δ 狼和ω 狼，猎物的位置对应着全局最优解。在利用GWO 算法求解优化问题时，假设优化问题维度为D，狼群整体数量为N，第i 只灰狼所在的D 维空间位置可以用xi=（xi1，xi2，…xiD）来表示。在搜索过程中，灰狼群体的狩猎行为可表示为

其中，xp（t）表示在第t 次迭代时猎物的位置；xi（t）表示第t 次迭代时灰狼的位置；A和C是GWO 算法中的两个参数向量，可表示为

其中，r1和r2为［0，1］之间的随机数；a 被称为收敛因子，在迭代过程中，其值从2 线性减小到0，有

其中，t 表示当前算法迭代次数，tmax表示算法的最大迭代次数。

灰狼群体中的其他个体xi根据α 狼、β 狼和δ 狼的位置更新自身位置，即

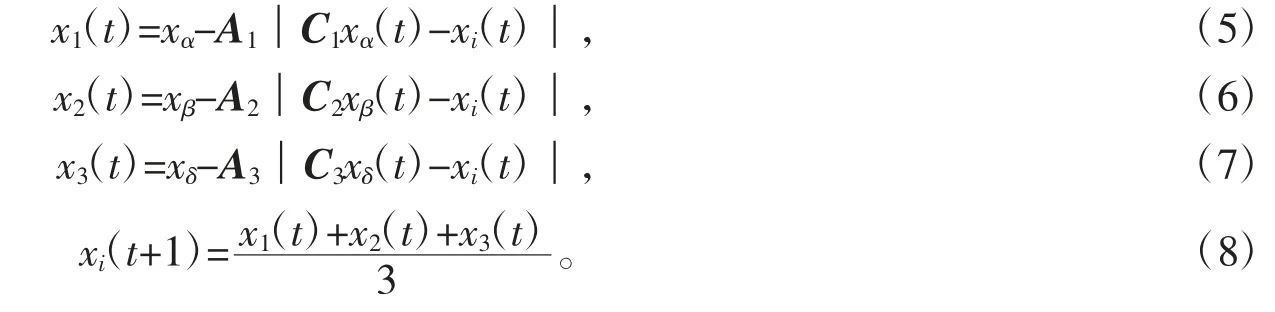
其中，A1、A2和A3含义与A 相同，C1、C2和C3含义与C 相同。

2 改进灰狼优化算法

为了进一步提高GWO 算法的性能，从控制参数调整和位置更新策略两方面对GWO 算法进行了改进，提出了一种基于反余弦收敛因子和变异策略的改进灰狼优化算法（CMGWO）。

2.1 反余弦收敛因子

在GWO 算法中，参数向量A 在平衡全局探索能力和局部开发能力之间发挥着重要的作用。由式（1）可以看出，当│A│＜1 时，灰狼群体将缩小狩猎范围进行精确搜索，此时对应算法的局部开发能力；当│A│≥1 时，灰狼群体将扩大狩猎范围，此时对应算法的全局探索能力。由式（2）可知，参数向量A 的大小主要取决于收敛因子a，即a 的取值将影响整个GWO 算法的全局探索能力与局部开发能力。由式（4）可以看出，收敛因子a 采用线性递减策略由2 逐渐减小到0。然而，GWO 算法在寻优过程中会发生非线性变化，收敛因子的线性递减策略在一定程度上限制了GWO 算法的寻优能力。受反余弦函数的启发，提出一种基于反余弦收敛因子的控制参数调整策略，具体更新可表示为

该策略可以非线性地调整自身取值，在搜索前期，能够生成较大的值以保证GWO 算法的全局探索能力，加快算法收敛速度；在搜索后期，能够生成较小的值以增强算法的局部开发能力，提高解的精度。

2.2 位置变异策略

在GWO 算法中，狼群个体主要跟随最优解α 狼来更新自己的位置。由式（5）～（8）可以看出，在进化后期的搜索过程中，基于最优个体保存策略，狼群个体将会大量聚集于α 狼周围，导致狼群搜索多样性的缺失。尤其当α 狼不能寻找到全局最优解而陷入局部最优解时，将会使得整个算法陷入局部最优，导致算法早熟收敛和寻优精度下降。为了解决这一问题，受粒子群优化算法和差分进化算法的启发，充分利用灰狼个体之间的差异信息，设计了一种新的位置变异策略，具体可表达为

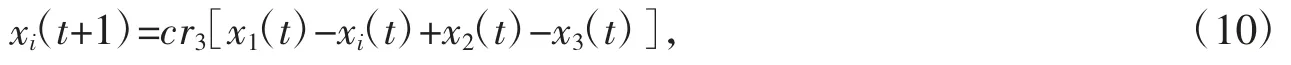
其中，c∈［0，1］为随机系数，r3为［0，1］之间的随机数。

由式（10）可以看出，所提位置变异策略充分考虑了狼群个体中的信息，借鉴β 狼和δ 狼之间的差异性，提高了种群搜索的多样性；同时利用最优个体α 狼与当前灰狼个体位置之间的差异性信息，增强了算法跳出局部最优解的能力。

2.3 改进算法步骤

由此可得出改进灰狼优化算法（CMGWO）的步骤为：1）设置CMGWO 算法的相关参数，狼群规模N、优化问题维度D、狼群搜索范围［xmin，xmax］、算法最大迭代次数tmax；2）在给定的狼群搜索范围［xmin，xmax］随机生成初始群体；3）计算每个灰狼的适应度值（fx）i，根据适应度值的大小，确定α 狼、β 狼和δ 狼，并将各自的位置分别记为xα、xβ和xδ；4）根据式（5）～（8）更新灰狼个体的位置；5）结合式（9）和（2）更新参数向量A，并根据式（3）更新参数向量C；6）根据式（10）更新灰狼个体的位置；7）判断算法是否达到设定的最大迭代次数tmax，如果达到，算法终止，输出最优结果；否则，跳转至步骤3）。

3 仿真实验

为了验证CMGWO 算法的性能，本文选取16 个典型的benchmark 测试函数进行仿真实验对比，表1 给出了16 个函数的相关信息。其中f1～f9是单峰优化函数，f10～f16是多峰优化函数。

表1 测试函数

从两个不同的方面设置了对比实验：1）比较CMGWO 与RMDE［5］，GWO［1］和WOA［6］在16 个测试函数上的收敛精度收敛速度；2）比较CMGWO 与NGWO［3］、PSO_GWO［7］、mGWO［8］、EGWO［9］和LGWO［4］在8 个测试函数上的收敛精度。

3.1 实验参数设置

各算法的参数具体设置如下：1）PSO 算法参数设置包括学习因子与惯性权重；2）RMDE 算法参数设置包括交叉算子和最大概率系数；3）GWO 算法、WOA 算法、NGWO 算法、PSO_GWO 算法、mGWO 算法、EGWO 算法和LGWO 算法的参数设置与原文献相同。

3.2 与RMDE、GWO 和WOA 性能对比

为了验证CMGWO 的性能，将其分别与RMDE、GWO 和WOA 进行对比。每个算法独立运行30 次，取结果的平均值和标准差作为评价标准。表2 给出了所有算法在16 个测试函数上的优化结果。

从表2 可以看出，所提CMGWO 算法在16 个函数上均取得了最好的函数优化结果，特别是在f1、f2、f5～f8、f10～f14、f16这12 个测试函数上，CMGWO 算法能够搜索到理论极值。而且，在f3和f4这2 个测试函数上，CMGWO 搜索到的最优解已经很接近于理论极值了。RMDE、GWO 和WOA 在16 个测试函数函数上均未能搜索到全局最优解。

为了更加直观地展示各种算法在收敛速度方面上的差异，图1 依次给出了所有算法在8 个测试函数上的收敛曲线。从图1 可以看到，CMGWO 算法在这8 个测试函数上收敛速度都是最快的。综上所述，与RMDE、GWO 和WOA 这3 种优化算法相比，CMGWO 算法有着更高的收敛精度和收敛速度。

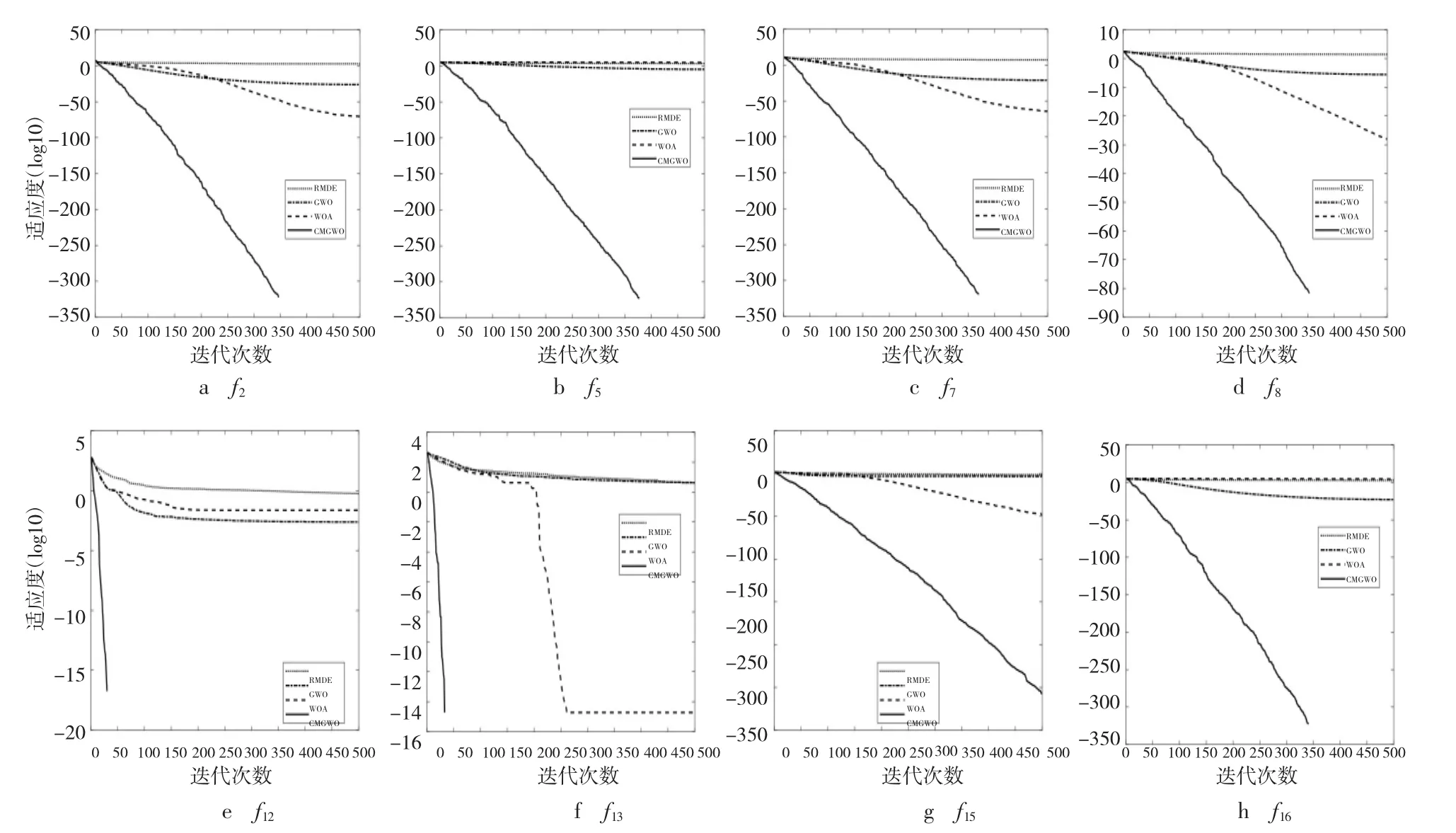
图1 4 种优化算法在8 个测试函数上的收敛曲线

3.3 与NGWO、PSO_GWO、mGWO、EGWO 和LGWO 性能对比

为了进一步验证所提CMGWO 算法的寻优性能，将其分别与5 种改进GWO 算法进行对比。为了保证实验的公平性，5 种改进GWO 算法的函数优化结果均来自于各自的原文献。同时为了更加可靠地评价算法的优化性能，只选取了这5 种改进算法在共同的8 个测试函数上的测试结果。每个算法均独立运行30 次，取30 次后的平均值和标准差作为评价标准，如表3 所示。

表3 CMGWO 与NGWO、PSO_GWO、mGWO、EGWO 和LGWO 结果对比

从表3 可知，CMGWO 算法在7 个测试函数上（f1、f3～f5、f12～f14）都能取得最好的优化结果，特别是在f1、f5、f12～f14这5 个函数上能够寻找到理论极值，在f3和f4这两个测试函数上很接近于理论极值。仅在测试函数f10上，优化结果差于PSO_GWO 和EGWO。NGWO 和mGWO 算法仅能在f13和f14这2 个测试函数上搜索到理论极值。PSO_GWO 算法仅在f10这个测试函数上取得了最好的优化结果但未能搜索到理论极值。EGWO 和LGWO 在8 个测试函数上均未能取得最好的优化结果。

综上所述，与5 种已有的典型改进GWO 算法相比，CMGWO 算法在8 个测试函数上有着更好的表现，能够进一步增强GWO 跳出局部最优解的能力。

4 小结

针对GWO 算法存在的不足，本文提出了一种基于改进收敛因子和变异策略的新型灰狼优化算法（CMGWO），并在16 个测试函数上进行了仿真实验，结果表明，与3 种智能优化算法和5 种典型改进GWO 算法相比，所提出的CMGWO 算法具有更快的收敛速度和更高的收敛精度。