基于大主应力迹线的无黏性土挡墙土压力分析

李 敏，曹文贵，王林庆，张慧姐

(湖南大学 土木工程学院，长沙 410082)

1 研究背景

挡墙土压力分析一直是土木学科中的重要研究方向，目前研究挡墙土压力的方法主要有朗金、库伦土压力理论，这两种经典理论是实际工程中应用最为广泛的方法，突出优点在于参数概念清楚、计算方法简明。朗金土压力理论中存在与实际不符的挡墙墙面绝对光滑的假定，实际工程中墙面粗糙，墙土摩擦必然存在，并且已成为挡墙土压力分析计算中十分重要的影响因素。由于墙土间存在摩擦力的作用，故接触面处的应力首先发生偏转，进而引发其他土体微元的方向发生变化，直至所有土体达到极限平衡状态形成形状不规则的楔体块。库伦土压力理论虽然考虑了墙土摩擦效应的影响,但认为破坏面为直线，且破坏土体整体为一顶点为墙踵的三角形楔体，实际工程墙后土体破坏面难以确定，与土体参数等多种因素有关。众多学者也就如何合理探究墙土间摩擦对土压力的影响做出了不同的研究。

卡岗[1]于1960年首次提出了土压力计算的水平分层分析法后，许多学者在此基础上对水平分层法进行了诸多改进[2-18]。Paik等[2]则继续延用库伦滑裂面和滑裂角，将墙后土体的小主应力迹线从圆弧线简化为水平直线，并划分直线薄层单元，通过将应力平均化和平衡条件建立土压力强度理论。Goel等[3]则以抛物线函数建立出滑裂面表达式，通过将微分单元上的应力平均化并利用应力比求得主动侧向土压力强度，提出了新的土压力分析方法。Wang[4]也在库伦理论基础上沿竖向划分直线薄层单元体，进而提出土压力强度新理论。但由此产生的直线薄层单元仍然面临受力复杂、应力分布计算困难的问题，往往需要对单元受力情况进行各种假设。例如，假定薄层单元上下界面不存在剪应力[2-8]、上下界面应力均匀分布[9-13]和不考虑主应力在滑动面上的偏转[13,15-16]等。这显然有悖于实际情况，因为只有在主应力的作用面上才存在剪应力为0，墙土间摩擦导致应力方向发生偏转后，水平分层所得平面显然不是土拱效应下的主应力作用面，也不存在应力沿直线均匀分布的规律。为了解决这类不足，Li等[16]和Cao等[17]进一步提出了倾斜直线分层方法，虽简化了受力分析，避免了忽视剪应力的问题，但由于土颗粒在倾斜单元界面上不可能都处于主应力状态，因此，这也是一种近似处理方法。

综上所述，划分直线薄层单元的水平或倾斜分层法因不能严格沿主应力方向分层导致应力分析缺乏合理性，并且人为假定了墙后土体中通过墙踵的直线形滑动面形状。因此，为获得更为完善的挡墙土压力分析方法，本文采用沿主应力方向分层的曲线型薄层单元分析方法深入探讨挡墙土压力分析新思路，建立基于更严谨客观规律的挡墙土压力分布新模型。

2 应力传递与主应力迹线的确定

2.1 应力传递规律

由于挡墙墙面在实际工程中不可能绝对光滑，与墙背接触的土体表面必然受摩擦力的影响，使得土中主应力方向发生偏转，不再遵循水平或竖直的方向规律。本文提出用最大主应力迹线表达发生偏转后的应力传递规律，并进行挡墙土压力分析。大主应力迹线是指将各处土体发生偏转后的大主应力切线的切点连接成的线，此概念与Paik等[2]提出的挡墙土压力分析方法中主应力拱的概念相符。目前，常采用的主应力迹线型式有圆弧线[2,6-8,12-13,18]、悬链线[9,19]、抛物线[3,5]等，而将主应力迹线假设为“圆弧线”仍为目前土压力研究过程中的主流手段。综上，本文为简化研究，依据相关主应力迹线研究成果，采用圆弧线的主应力迹线，同时考虑到实际挡墙工程情况的复杂性和不确定性，提出以下假定：

(1)挡墙墙背竖直，墙面粗糙，墙土间摩擦角为δ，且墙后填土表面水平。

(2)挡墙墙后土体性质为均匀砂土，即无黏性土，其内摩擦角为φ。

2.2 大主应力迹线的确定方法

挡墙后土体受到墙土摩擦效应的影响，其应力从墙土连接面开始偏移至土体达到极限平衡状态，墙后各点土体大主应力因墙背处墙土连接面摩擦力发挥作用而发生偏移，方向不再全部竖直向下。由于填土为均质土，假定主应力方向变化连续且无突变。大主应力方向在地表处垂直于水平面即竖直向下，随着土层逐渐加深，土体大主应力方向逐渐发生变化，相邻点的方向变化是连续的渐变，直至墙土连接面，此时大主应力方向与水平方向成锐角。各方向连续变化的规律可用迹线表示，迹线上各点的切向方向代表此点处大主应力的方向。由于本文采用沿大主应力迹线的分层方法，必须首先确定大主应力迹线圆弧(包括其圆心与半径)的求解方法。

为确定主应力迹线的几何参数，建立图1进行分析，在墙后土层深度h处取一初始厚度为Δh的曲线微分薄层单元作为研究对象，分析墙土连接面上A点的应力状态，A点是大主应力迹线与墙背的交点，该点的切向方向(即大主应力方向)与水平方向的夹角设为θa，则在沿主应力迹线逐渐变化到填土面上B点的过程中，最大主应力方向与水平方向的夹角由θa变化为π/2。由于填土表面应力竖直向下，其切向方向为水平线，而求得墙土接触处应力偏转角为固定值，其切向为斜线，两切线必然相交于一点，根据圆弧半径与切线相互垂直的定理，必然得到应力迹线为非同心圆弧，且圆心位于水平线O1B上。通过对主应力迹线圆弧的A点和B点各自作该点切线方向的垂线，切线方向代表主应力的方向，垂线交点即是主应力迹线圆弧AB对应的圆心O2，同理可得主应力迹线圆弧A′B′对应的圆心O1，垂线O2A和O1A′的长度即是迹线AB、A′B′分别对应的半径值R1、R2。由三角函数关系可得：

图1 墙后填土的主应力偏转规律分析Fig.1 Analysis of principal stress deflection of soil behind the wall

(1)

(2)

上述内容即为挡墙墙后土体应力发生偏转后的传递规律，本文研究发现墙土摩擦效应发生时，各点土体的主应力方向也发生变化，由于逐渐变化形成了多组迹线，如图1所示。

在图1中墙土接触处取一直角三角形单元体，三角形斜边与墙土接触面重合，两条直角边的法线方向分别为大小主应力方向。三角形单元斜边长度取为Δh，分析三角形单元体的受力，由力学中的静力平衡方程可得到：

(3)

(4)

τa=σatanδ。

(5)

联立式(3)—式(5)，整理后得

(6)

由于此时在墙土接触面沿着墙背的平面上，各个土体单元都达到了极限平衡，各点的大小主应力均应满足摩尔-库伦定律，即应力比N为

(7)

利用式(6)—式(7)可得

(8)

由此可知θa为常数，与土体参数有关，也说明墙土接触面处大主应力方向的偏转角达到最大值后不再随深度发生变化。墙后土体大主应力迹线为一组非同心圆的圆弧曲线，小主应力迹线为与大主应力迹线垂直的另一组圆弧曲线，而且曲线型薄层单元上下界面上小主应力σ3值随迹线发生变化，同时切线方向也在不断变化。上述关于主应力迹线圆弧的几何参数的确定，也是本文挡土墙墙后土体曲线分层和模型建立的基础。

3 主动土压力分析模型

在确定了主应力迹线圆弧的几何参数之后，采用大主应力迹线对挡墙墙后土体进行分层，所得曲线型薄层单元受力明确，各点土体处于主应力状态，不再存在忽略剪应力或主应力均值化的问题，建立如图2所示的土压力分析模型。

图2 墙后土体中微分单元受力分析Fig.2 Stress analysis of a differential element in soil behind the wall

在圆弧形薄层单元体上，微段单元的内侧圆弧AB上受到最小主应力σ3分布力的作用，外侧圆弧A′B′上受到最小主应力σ3′分布力的作用。墙土接触面上微段单元的AA′边受到水平法向应力σa和摩擦应力τa的作用，如图2所示。如果在最大主应力迹线上任取一点C，并设O2C与O2A的夹角为θ，则C点最小主应力σ3随θ变化而变化，为θ的函数。如果设C点埋深为h′，则依据重力场特点并参考现有研究[17,20]的相应做法，C点的最小主应力σ3可表示为

(9)

式中：γ为土体重度；C1为待定常数；h为土层深度。

同理，可将薄层单元下界面上E点最小主应力σ′3表示为

(10)

式中s为薄层单元厚度，由延长直线O2C，与薄层单元外侧圆弧A′B′相交获得，利用正弦定理求解△O1O2E并忽略高阶微量可得

(11)

然后依据其静力平衡条件，可建立薄层单元的静力平衡方程，下面将对薄层单元所受作用力的确定方法分别进行介绍。

薄层单元体在水平竖直方向满足受力平衡条件，由∑f(x)=0可得

(12)

由∑f(y)=0可得

(13)

(14)

(15)

设s′为薄层厚度s方向上的微量值，重力可采用双重积分求得，即

(16)

式中S条带是指薄层单元AA′B′B的面积。

AB边上应力在x方向上的合力为

叶红伟不光是种沙葱，也种锦绣海棠，种元宝枫，种文冠果。如今，他成了科尔沁沙地上的名人。电视台记者拿着话筒采访他，他摆摆手说：“没什么好说的，沙子不固住，说啥都没用。”

(17)

A′B′边上应力在x方向上的合力为

(18)

同理，AB边上应力合力在y方向上的合力为

(19)

A′B′边上应力在y方向上的合力为

(20)

式中θ1为O1E与填土面的夹角，利用△O1O2E的几何关系正弦定理求解θ1,并忽略高阶微量可得：

cosθ1=sin(θa+θ) ,

(21)

sinθ1=cos(θa+θ) ,

(22)

利用式(12)—式(23)可分别求得前述单元所受各作用力，将各作用力分别代入xy向平衡方程式中，得到关于C1和σa的联合方程，先迭代求解C1，得到式(24),即

(24)

忽略高阶微量对其进行整理，可求得

(25)

进而求得

(26)

利用关系式τa=σatanδ求得

(27)

如果令

(28)

则σa和τa为方便表达可简化为：

σa=γhKa,

(29)

τa=γhKatanδ=γhKaf。

(30)

式中：Ka为主动土压力系数;Kaf为主动摩擦土压力系数。

为使本文方法更具一般性，借鉴朗金理论的处理，当填土面上均匀分布超载q作用时，将超载q等效为重度为γ和厚度为h0的土体的作用，h0可表示为

(31)

于是，将式(29)、式(30)中的h以h+h0代替，即可应用到填土面均布超载q作用的工程实际情况中，以便进行工程实际中土压力的应用计算。

4 土压力合力和对墙角的弯矩计算

工程中挡墙墙后场地表面常有堆载或其他作用力，本文为求得合力计算公式，假设表面均布荷载q，利用上述推导所得的公式建立应力分布示意图，随着土层深度从地表表面向下增加，挡墙法向主应力强度的分布规律如图3(a)所示，挡墙主动摩擦应力强度的规律分布如图3(b)所示，图中的H为挡墙墙高，h0为荷载q的等效高度。

图3 主动土压力分布和主动摩擦应力分布Fig.3 Distributions of active earth pressure and active frictional stress

根据图3进行土压力合力E的计算，可得

(32)

为研究挡墙倾覆稳定性,常需要进行弯矩的计算，对墙角取矩，可求得主动土压力相对于墙角的弯矩M为

(33)

5 验证与讨论

5.1 验证分析

为验证本文方法的有效性，本节将引入具体试验数据进行分析对比，采用文献[18]试验和文献[14]中提供的参数值和墙体土压力试验中的实测值，分别采用本文方法、库伦方法、朗金方法及文献[2]、文献[15]方法进行计算，求得各个方法所对应的土压力计算值，并进行对比分析。试验各参数如表1所示，计算结果如图4所示。

表1 试验参数Table 1 Experimental data parameters

由图4可知，文献[2]和文献[15]的理论计算结果都反映了土压力分布非线性的规律；但文献[15]的理论计算结果在挡墙上部偏离较大，它展现的主动土压力随深度变化的规律缺乏合理性。Janssen[21]研究表明侧压力随深度增加呈现逐渐增大的趋势，在靠近墙踵底部时增幅变小。而文献[2]、文献[15]方法中土压力在墙底部某一点骤减并接近0，这与料仓理论[21]中对侧压力规律的研究相违背。图4中采用本文方法获得的理论分析结果处于朗金理论计算值和库伦方法计算值之间，而且在不同位移模式下更符合实测数据，较好地反映了侧压力分布随深度增大的趋势，相较于其他方法更能反映墙土摩擦对土压力的影响，证明了本文方法的适用性。在目前试验水平下难以实现土压力分析方法所设定的极限条件和空间要求，故本文进一步通过算例分析本文方法正确性，采用挡墙墙高H=6 m，土体重度γ=18 kN/m3来进行计算，将经典朗金和库伦土压力理论、文献[2]和文献[15]方法以及本文方法理论计算结果进行对比，以更好地分析各方法优劣所在，具体计算所得曲线见图5。

图4 不同试验中主动土压力分布曲线对比Fig.4 Comparison of active earth pressure among different methods in different tests

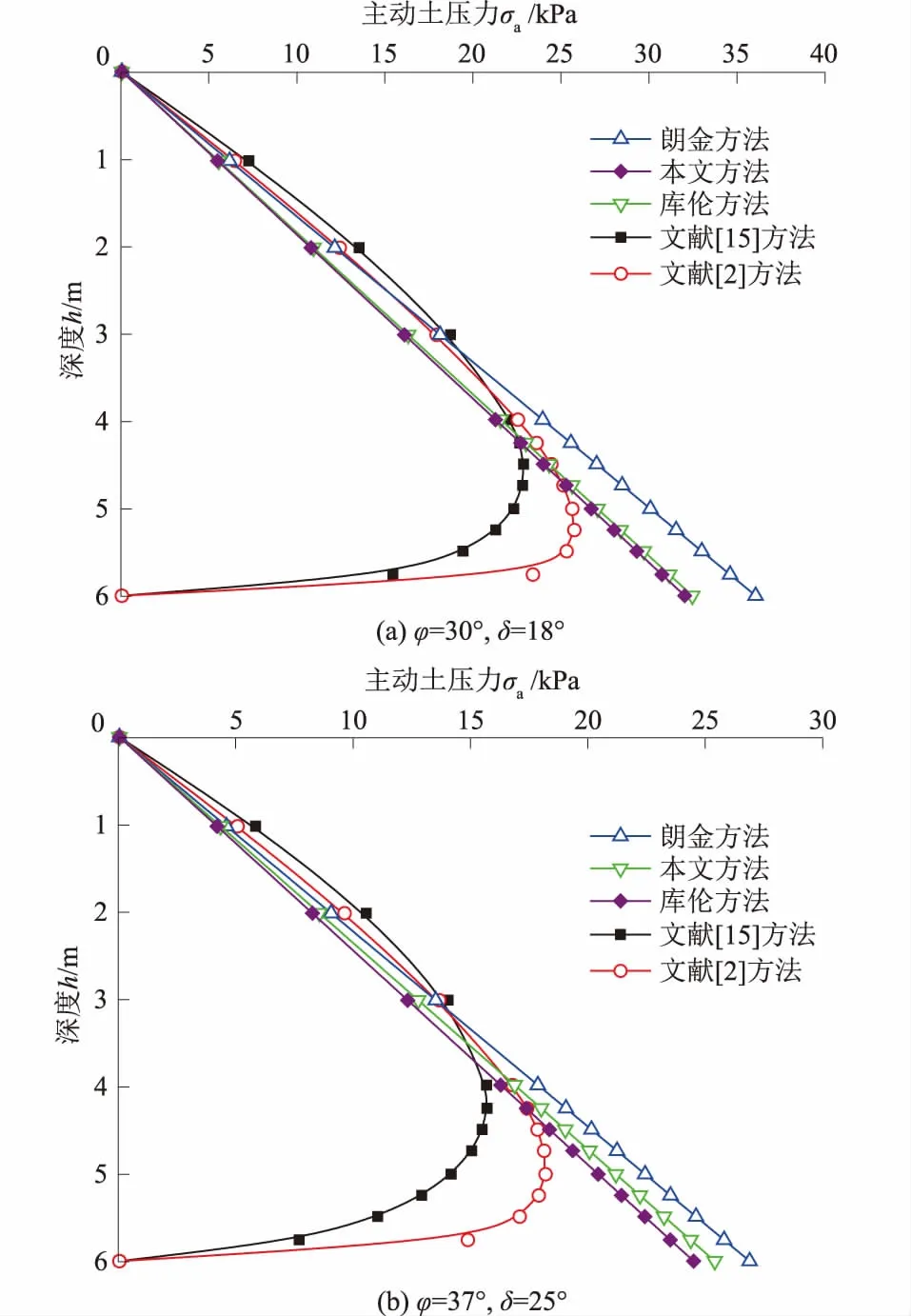
图5 不同参数下主动土压力分布曲线对比Fig.5 Further comparison of active earth pressure with different parameters among different methods

从图5可以看出：在不同参数值影响下，因假定忽略摩擦效应的影响，朗金土压力理论计算值均偏大，而文献[15]方法分析的结果在挡墙中上部偏大程度更多；文献[2]方法分析的结果与朗金方法计算值相近，且在接近挡墙底部急速变小，与前文所述料仓侧压力的分布规律不符。本文方法土压力分析结果在不同参数下均与库伦方法分析结果较为接近，且对于墙土摩擦效应作用(即δ值变化时)的表现明显，证明本文分析方法的理论严谨性。

5.2 参数分析

为了进一步探讨各影响因素对主动土压力2个系数的影响规律，本节选取工程中常用参数范围，分别进行不同分析方法的系数计算值的对比，并通过控制变量来探讨各影响因素对土压力各系数的反映规律和影响程度,见图6—图8。

图6 主动土压力系数Ka随φ和δ的变化曲线Fig.6 Curves of active earth pressure coefficient Ka versus φ and δ

由图6(a)可知，当δ为定值时，随着φ增大，参与对比的5种方法水平主动土压力强度系数Ka都随之减小，本文分析方法所得系数值与库伦方法以及文献[2]计算结果接近，变化趋势与王梅等[7]、刘洋等[11]探讨的规律一致。由图6(b)可知，内摩擦角φ为固定值时，随着δ值变化，朗金方法因理论中缺少对墙土间摩擦的考虑，系数计算值并不会发生变化，保持定值且计算结果偏大。而文献[15]方法中考虑了摩擦效应，计算所得系数却比不考虑摩擦效应的朗金方法计算值偏大，存在不合理性。本文方法系数计算值接近库伦方法计算所得的系数值，且变化趋势与王梅等[7]、刘洋等[11]探讨的规律一致，随墙土间摩擦角δ值增大而增大。由图7可知，参与对比的4种方法主动摩擦系数计算值Kaf随墙土接触面摩擦角δ的变化趋势一致，随无黏性土土体性质指标φ的变化趋势也一致，且本文方法计算值接近库伦方法计算值，证明本文方法合理性。

图7 主动摩擦土压力系数Kaf随φ和δ的变化曲线Fig.7 Curves of active fritional earth pressure coefficient Kaf versus φ and δ

图8为采用本文方法获得的Ka、Kaf随δ值、φ值的变化曲线，可以看出，主动土压力系数Ka对墙土接触面外摩擦角δ变化时的反应程度小于对土体内摩擦角φ发生变化时的反应程度，而δ值对Kaf的影响要大于对Ka的影响，显然是合理的。

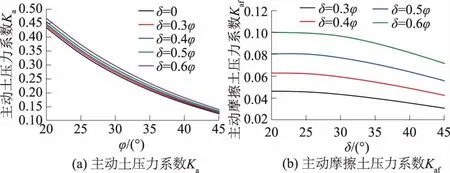
图8 Ka和Kaf随φ和δ的变化曲线Fig.8 Curves of Ka and Kaf versus φ and δ

6 结 论

本文充分考虑墙土间摩擦引起挡墙墙后土体主应力方向偏转的力学机理，结合先进理论引进主应力迹线的概念，提出了受力分析更合理的分层分析方法。与前人学者不同，本文不进行滑裂面的设定，通过对滑动土体进行曲线分层和薄层单元的受力分析，建立分析理论基础更完善的土压力分析方法，并得到以下结论：

(1)研究墙土摩擦效应作用下墙后土体应力的变化规律，提出了最大主应力迹线的具体几何确定方法，进而建立了曲线分层法，理论基础更加严谨，解决了水平直线分层法中因薄层受力分析复杂而使应力近似处理或忽略的问题。

(2)建立了圆弧薄层单元的主动土压力分析模型，获得了主动土压力系数和主动摩擦土压力系数的理论计算公式。通过本文方法与其他方法进行系数计算，进一步研究了内摩擦角和墙土间摩擦参数对主动土压力系数和主动摩擦土压力系数的影响。

(3)通过模型的受力分析，推导得到作用在挡墙上任意深度的主动土压力分布强度计算公式，进而得到相应的主动土压力合力和对墙角的弯矩公式。将本文方法与现有分析方法和试验数据对比，所得值与试验值、库伦方法计算值最为接近。因充分考虑了摩擦效应的作用，本文方法对δ值变化时的反应明显，验证了本文方法的合理性。

(4)由于本文研究中假定墙后土体主应力迹线为圆弧曲线，对主应力迹线型式还需进一步研究。本文针对竖直墙背且墙后土体为无黏性土进行理论分析，在黏性土或者倾斜墙背中的应用仍需扩展研究。实际工程中发现随着土层深度增加至接近挡墙底部时，土压力分布逐渐表现为非线性，本文对这一规律仍需深入研究。由于本文计算公式复杂，实际应用时仍需进一步优化。