基于CEEMDAN-BA-SVR-Adaboost模型的白水河滑坡位移预测
李龙起,王梦云,赵皓璆,王 滔,赵瑞志
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059)
1 研究背景
滑坡是一种常见的自然地质灾害,在我国西南山区较为常见,其破坏力和造成的经济后果极为严重。据统计,我国至少有1/5地区受到滑坡灾害的威胁[1],严重影响了当地人民的生命财产安全。因此,通过对滑坡位移进行预测分析以达到防灾减灾的目的是国内外学者较为关心的问题。
一般来说, 滑坡的位移变化受到多方面因素的影响, 呈现出非线性非稳态的特征[2]。 在实际的滑坡预测中, 传统的预测方法如灰色模型GM(1,1)、多项式拟合等, 由于缺乏对数据样本的学习过程, 难以高效地实现非线性的滑坡波动项位移预测。 近年来, 智能算法因其具有较强的非线性映射能力被广泛应用到滑坡位移的预测中[3]。 徐峰等[4]利用多项式拟合预测滑坡位移的趋势项, 并采用BP神经网络对周期项进行预测。 李仕波等[5]基于时间序列分析将滑坡位移分解为趋势项和周期项, 建立GM(1,1)和AR模型分别对其进行预测。 李仕波等[5]用HP滤波分析法将趋势项和波动项位移分离, 利用多项式拟合预测趋势项, 建立LS-SVM模型对波动项位移进行预测。 李骅锦等[6]用小波函数分解位移, 并采用ELM和OS-ELM模型分别预测趋势项和周期项。 上述研究方法较传统的经验方程预测、 非线性预测等在预测能力方面有较大提升, 但其均将滑坡位移直接分解为趋势项和波动项, 预测精度不高; 且所采用的人工蜂群(ABC)、粒子群优化(PSO)、遗传(GA)等传统算法在解决多峰值问题的寻优过程中容易陷入局部最优, 从而直接影响预测的准确性。 此外, 以上研究中建立的BP神经网络、 极限学习机等传统神经网络存在参数较多、 预测效果不理想等缺点。
基于上述问题, 本文以白水河滑坡为例, 利用CEEMDAN分解滑坡位移, 建立BP神经网络对趋势项进行预测, 然后提出CEEMDAN-BA- SVR-Adaboost(CBSA)预测模型对波动项进行预测, 并将该模型与CEEMDAN-PSO-SVR-Adaboost(CPSA)、 CEEMDAN-BA-BP-Adaboost(CBBA)、 CEEMADAN-BA-SVR(CBS)、BA-SVR-Adaboost(BSA)模型的预测精度进行对比, 随后再利用ZG118监测点数据对所建模型进行验证, 最后将趋势项与波动项的预测结果相加得到最终滑坡累计位移预测值, 以此证明CBSA模型的准确性、 优越性以及适用性。
2 预测模型的建立
2.1 算法介绍
2.1.1 CEEMDAN算法
由Huang等[7]提出的新型自适应信号时频处理方法——经验模态分解法(EMD)依据数据自身的时间尺度特征来进行信号分解,可以用来分析处理非线性非平稳数据,但其无法根据特征尺度有效分离出不同的模态成分。集合经验模态分解法[8](EEMD)是在EMD的基础上将白噪声加入整个时频内,有效解决了EMD的模态混叠现象,但白噪声难以加入且分解效率低下,噪声难以完全消除。因此,Torres等[9]提出了自适应噪声总体集合经验模态分解法(CEEMDAN),在每一阶段添加自适应高斯白噪声,有效解决EMD模态混叠现象的同时克服EEMD分解效率低和噪声难以完全消除的问题。
2.1.2 蝙蝠算法优化的支持向量回归机(BA-SVR)
Vapnik[10]于1995年针对二分类问题首次提出支持向量机(SVM)模型,核心思想是确定一个最优超平面,使得样本与超平面间的距离最大。而支持向量回归机(SVR)是SVM的一个重要分支,它所寻求最优超平面不是使两类样本点分得最开,而是使所有样本点离超平面的总偏差最小,求最优超平面等价于求最大间隔。因此,在滑坡的位移预测方面,SVR具有较高的适用性。然而,决定SVR模型性能的惩罚因子C和核函数g通常是随机生成的,其值的选取对模型性能影响较大。
蝙蝠算法(BA)是2012年由Yang[11]教授提出的模拟自然界中蝙蝠利用超声波探测猎物、避开障碍物的随机搜索算法。相较于粒子群算法、遗传算法等,BA可以在局部搜索与全局搜索间动态转换,具有结构简单、收敛速度快、搜索能力强、容易得到全局最优解及良好稳健性等优点。该算法基于并行搜索原则,蝙蝠群体内所有个体同时进行搜索。初始阶段在可行域内随机初始化所有蝙蝠的速度及位置,位置用来表示所求解。通过对比每一个蝙蝠,确定群体最优解,进而获得当前全局最优解。因此采用BA对SVR的参数进行寻优,具有全局优化能力,减少了参数的盲目试算,大大提高了SVR模型的预测准确性。
2.1.3 Adaboost
Adaboost是通过对训练样本集的操作来进行集成学习的。首先通过训练初始样本集得到第一个弱学习器[12],适当增加错分样本的权重,根据调整权重后的样本训练得到第二个弱学习器,重复学习直至弱学习器数目达到指定值。最终的集成学习器是对每个基学习器进行整合的结果。
BA-SVR模型虽已经具备较好的预测能力,但当样本量较小时,该预测模型不够稳定。使用Adaboost集成学习算法能够使BA-SVR模型重复使用样本数据,并通过集成多个BA-SVR模型做出最终预测,不仅提高了准确率,还增强了BA-SVR模型处理小样本数据的稳定性,从而改进预测效果。以BA-SVR模型作为弱学习器,利用Adaboost集成学习算法对多个弱学习器进行集成,最终组合成一个强学习器,并利用该强学习器预测滑坡的位移。
2.2 预测方法流程
(1)选定输入样本,对位移样本数据进行预处理。将处理后的样本数据分为训练集和测试集,假设测试集样本数为N,初始化测试数据的分布权值D1为
D1=(ω11,ω12,…,ω1i)。
(1)
其中,ω1i=1/N,i=1,2,…,N。
(2)初始化蝙蝠群,设置BA和SVR的初始相关参数。
(3)采用蝙蝠算法优化SVR的相关参数c和g,使用训练样本对SVR进行训练,同时得到m个BA-SVR弱学习器。第m个弱学习器的各预测序列误差和errorm为
(2)
式中ωi、ei分别为第i个测试数据的权值和预测误差。
(4)计算第m个弱学习器的各预测序列权重wm。
(3)
(5)更新第m个弱分类器的测试数据集的权值。
i=1,2,…,N。
(4)
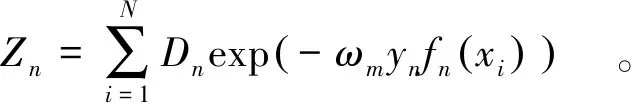
式中:yn为期望值;fn(xi)为输入数据xi的预测值。
(6)重复上述步骤,设定迭代次数阈值,得到第m个弱学习器的预测值fm(xi),最终得到的强学习器预测函数F(xi)为
(5)
假定Y为滑坡监测点监测到的实际累计位移,滑坡位移的预测流程如图1所示。

图1 预测方法流程Fig.1 Flowchart of prediction method
3 白水河滑坡概况
3.1 工程地质概况
白水河滑坡位于三峡库区秭归县长江右岸,与三峡大坝相距56 km,其三面环山,一面临水,十分利于降雨的汇集。地势由北向南逐渐增高,前后缘相差约330 m。该滑坡东西宽约700 m,两侧以基岩山脊为界进行划分,均为南北走向,纵长约770 m。滑坡整体坡度为30°~35°,平均厚度为30 m,体积约为1 260×104m3。
白水河滑坡属于堆积型类土质滑坡[13],其结构松散,滑体主要由碎石土及夹杂碎石的粉质黏土组成,滑带土大多为夹杂碎石或角砾的粉质黏土,下覆基岩为泥质粉砂岩,多呈中风化状,节理及裂隙发育较为明显。地形呈阶梯状,上部较陡,中部平缓,为崩积物的堆积创造了有利条件[14]。
该滑坡从古到今发生过多次滑动变形,为一典型顺层古滑坡。自2003年6月白水河滑坡地区库水位达到135 m以后,在水位突增及周期性调控的作用下,该古滑坡开始复活,并诱发了一系列新滑坡的产生。由此开始对该地区进行监测,滑坡监测点的布置如图2所示。根据滑坡变形特征以及监测数据结果,将滑坡划分为变形较为强烈的预警区A区(滑坡中前部)、与库水位相关性不大的变形区域C区(A区后缘、公路内侧)以及变形相对较为稳定的B区(滑坡后部)。

图2 白水河滑坡监测点布置平面图Fig.2 Plane layout of monitoring points for Baishuihe landslide
3.2 监测点数据
ZG93及ZG118监测点位于滑坡变形较为剧烈的预警区A区,且其从该滑坡监测初期开始进行布置,监测时间较长。为使监测点数据具备代表性和充分性,选取以上两个监测点的监测数据进行研究。本文以预警区ZG93监测点及ZG118监测点为对象,验证所建位移预测模型的优越性、准确性和适用性。本文记录该监测点从2005年3月—2013年3月每隔半个月的降雨量、库水位以及累计位移数据,共计192组,如图3所示。

图3 2005年3月—2013年3月滑坡累计位移、 降雨量、库水位监测曲线Fig.3 Curves of monitored cumulative displacement of landslide, rainfall, and reservoir water level from March 2005 to March 2013
4 白水河滑坡位移预测
根据滑坡变形特征,选取2005年3月—2012年3月168组数据作为本文模型的训练样本集,取2012年3月—2013年3月24组数据作为模型的预测样本集。
4.1 滑坡位移的CEEMDAN分解
诱发库岸滑坡位移发生变化的因素有很多,主要包括内部因素和外部因素两种。内部因素主要包括地形地貌、地层岩性、地质构造[3,15]等;外部因素主要包括降雨量、库水位等[16]。与外部因素相关联的坡体内地下水位、渗透压以及土体含水率等直接影响着滑坡的变形状态,因此在对滑坡致灾机理进行分析时应对内外部因素进行综合考虑。
在Matlab中建立CEEMDAN模型,取标准噪差为0.2,添加噪声序列的数目为500,最大迭代次数为5 000。将ZG93监测点192组位移数据分解为5个复杂度差异明显的IMF分项以及一个残余分项R,如图4所示,其中各小图共用同一个横坐标。5个IMF分项构成滑坡位移波动项,即由外部因素影响导致的滑坡位移变形。残余分项R位移变化曲线平滑,明显区别于其他五项,为滑坡位移趋势项,即由滑坡自身内部因素引起的滑坡变形。

图4 2005年3月—2013年3月ZG93监测点位移的 CEEMDAN分解结果Fig.4 CEEMDAN decomposition results of displacement of monitoring point ZG93 from March 2005 to March 2013
4.2 趋势项位移预测
趋势项位移具有长期稳定的特点,其曲线变化具有规律性,可采用简单模型对其进行预测。由于其趋势性较强,参考前人经验[16],将前15 d累计位移、前30 d累计位移、前45 d累计位移作为模型输入变量,在Matlab中建立3层BP神经网络,设置各层神经元个数,输入层为3,隐含层为8,输出层为1,学习率设为0.000 6,最大迭代次数为100。利用建立好的网络对前168组数据进行训练,然后采用训练后的网络对后24组数据进行预测,得到预测结果如图5所示。
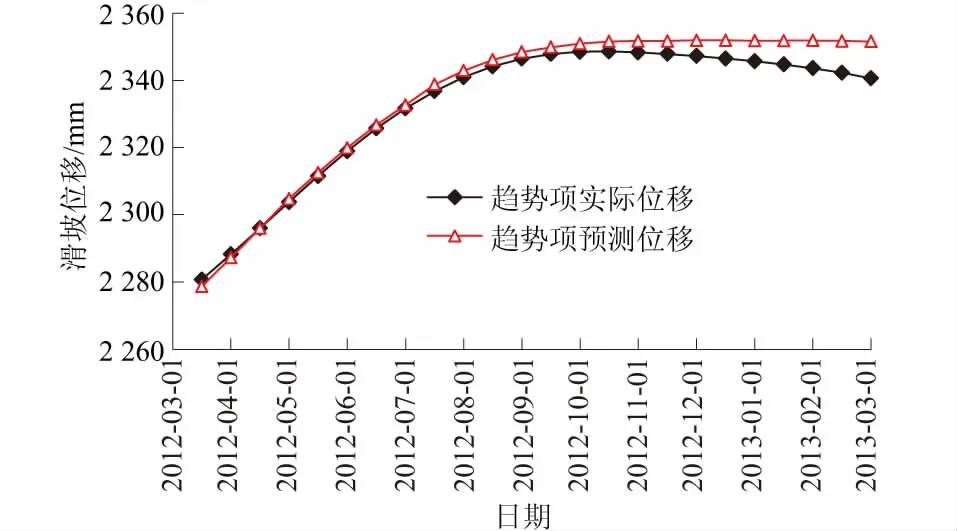
图5 趋势项位移预测效果Fig.5 Prediction result of trend item displacement
模型预测结果的拟合度R2为0.987 9,平均绝对百分误差MAPE为0.001 5,均方根误差RMSE为4.520 5,说明在对趋势项位移进行预测时,BP神经网络具有较好的适用性。
4.3 确定波动项影响因子
4.3.1 “波动”机理分析
结合前文所描述的滑坡地质特性分析,该滑坡坡体结构松散、透水性较强,在大气降雨及库区蓄水的交替作用下,水体通过土粒间隙不断入渗使滑体抗剪强度降低、下滑力增大。同时坡体前缘的黏土物质具有吸水膨胀失水收缩的特性,长期受库区蓄水周期性作用的影响,其抗剪强度及稳定性均将降低。此外,基岩裂缝的存在为地下水提供了良好通道,地下水的入渗在滑体内形成的不利孔压和渗透压力也将影响滑坡的稳定性[14]。
由于内部地下水补给的来源主要为降雨和库区蓄水,因此,本文仅将降雨量及库水位变化两者考虑作为波动项位移变化的影响因素。
4.3.2 监测数据分析
由图3可知,库水位具有明显的可分段特征。2005年3月—2006年9月,库水位在<140 m范围内波动(第1阶段);2006年10月—2008年10月,库水位得到大幅提升,且稳定在145 m与155 m之间(第2阶段);2008年11月—2013年3月,库水位又由155 m提升到175 m,且以175 m为最大值,波动范围稳定在30 m左右(第3阶段)。根据上述库水位分段特征,分3个阶段对ZG93监测点的监测数据进行分析:
(1)在第1阶段,随着汛期的到来,监测到的累计位移出现一定小幅增长,且对应时间段内的库水位呈下降趋势。库水位在此阶段内的下降幅度较小,且初始位置较低,因此对滑坡的影响十分有限。
(2)在第2阶段,滑坡位移有两次较为明显的增长,但在相同条件下,增长的幅度却有较大差异。第一次增长发生在2007年6—9月,库水位从155 m下降到145 m,随着汛期的到来,累计位移从650 mm左右上升到约1 140 mm。次年同时期位移发生第二次增长,但累计位移增幅显著减小。这说明滑坡在初次遭遇外界影响因素大幅变动时,其内部渗流场、位移场及应力场将产生较为剧烈的反应。但当滑坡在该条件下趋于稳定后,同类情况再次作用时,滑坡将不再产生大幅变形,增长幅度明显降低。
(3)在第3阶段,库水位发生更大范围的改变,但由于滑坡内部各力学场及性质已经经历过大幅度调整,滑坡变形反应的敏感度远小于第2阶段。因此,即使在汛期且库水位变动幅度更大的情况下,滑坡位移的增长幅度与第2阶段相比也明显下降,且随着库水位调动次数的增加而逐渐趋于稳定。
由上述分析可知,降雨和库水位是影响滑坡变形的主要因素[17]。监测期间每年8—11月份库水位呈增长趋势,且该时间段内降雨量较大,但此时滑坡位移变化趋于平缓,这是由于水位上升对边坡表面产生的水压力大于由自身应力等因素引起的迫使坡体向外滑动的力,从而抑制了滑坡的变形。
监测期间每年5—7月份,库水位呈下降趋势,对应时间段内位移增长迅速。分析原因为:坡体内部地下水位无法及时与外部库水位保持同步降低,原本作用在坡体外部的水压力突然消失导致临空面在坡体内部静水压力的作用下向外加速变形,从而致使滑坡稳定性降低,位移变化增大。
4.3.3 影响因子的确定
对比图3降雨量与滑坡位移曲线发现,每年汛期在降雨量明显降低后的一段时间内,滑坡位移变形速率仍保持一定的增长,由此推测降雨量对滑坡变形的影响存在一定滞后性。对比库水位与滑坡位移曲线发现,每年12月库水位达到峰值点并开始下降,而滑坡位移一般到次年2月才呈现出明显的增长趋势,由此推测库水位的升降对滑坡变形的影响也存在一定的滞后性。
考虑到滞后性的影响,与前人经验[18]相结合,假设位移变化滞后的时间跨度为15 d,本文以2005年3月—2013年3月每半月为一研究点,将两类影响因素初步设定为8个因子,如表1所示。

表1 影响因素初步划分Table 1 Preliminary division of influencing factors
将上述8个影响因子作为输入数据集,各IMF分项位移以及波动项位移作为输出数据集,设分辨系数ρ为0.5,计算灰色关联度[19],得到各IMF分项与各影响因子间的相关性大小。计算结果如表2所示。

表2 各影响因子与各IMF分项及波动项位移间的 灰色关联度Table 2 Degrees of grey correlation between influence factors and IMF item and fluctuation item displacements
由表2可知,各影响因子与各分项及波动项间的灰色关联度均>0.6,证明初步设定的8个影响因子与波动项以及各IMF分项间均具有较强的相关性,可作为预测模型的输入数据集[20]。
4.4 基于CEMDAN-BA-SVR-Adaboost的波动项位移预测
基于Matlab建立BA-SVR-Adaboost模型,设置种群规模n为20,最大迭代次数iter_max为100,初始脉冲音量A0为0.6*ones(n,1),初始脉冲频率r0为zeros(n,1),音量衰减系数α为0.85,搜索脉冲频率的增强系数γ为0.9,脉冲频率搜索范围为[-100,100],蝙蝠群体个数d为影响因子数量8。采用以上参数建立的BA算法模型寻找使SVR预测误差最小的参数c、g,优化预测模型。用BA-SVR基预测期对训练数据进行训练,然后运用Adaboost算法多次训练BA-SVR模型,将多个BA-SVR基预测器加权组合形成强预测器。设基预测期个数K=10,利用建立好的模型对各IMF分项进行预测,预测结果如图6所示。
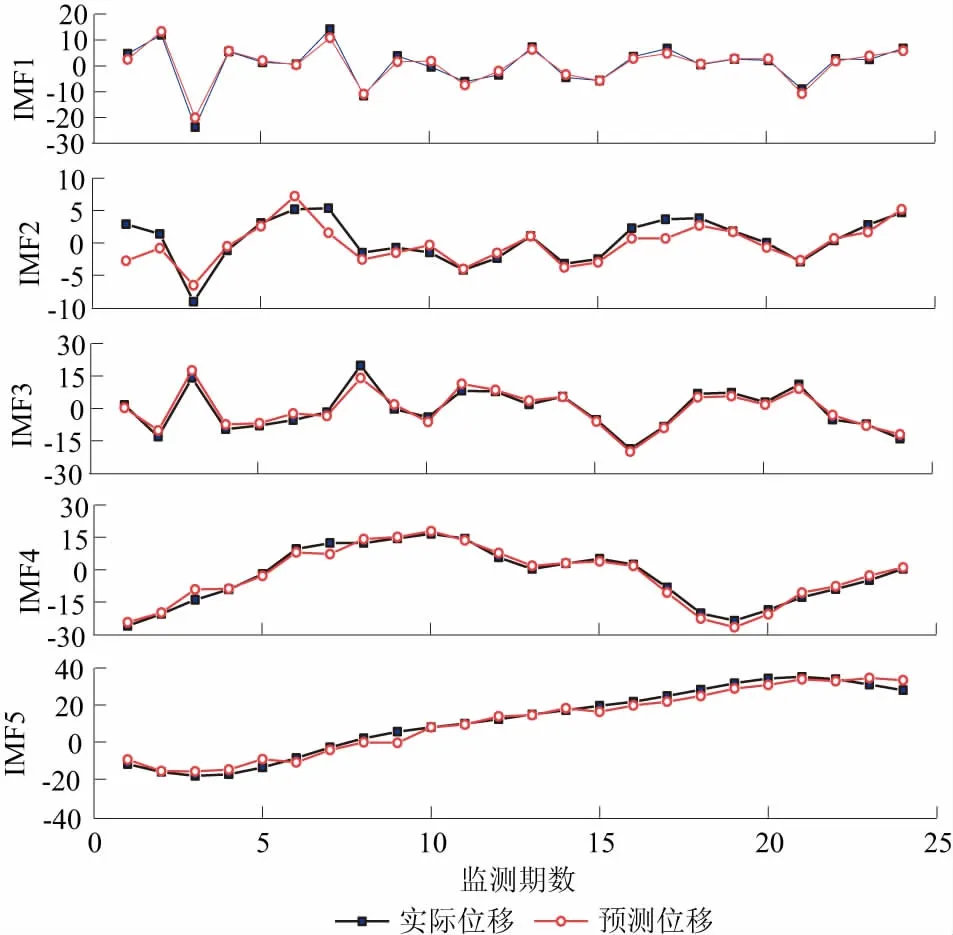
图6 各IMF分项预测结果Fig.6 Prediction result of IMF items
将各IMF分项预测结果相加,得到波动项位移的预测结果,如图7所示。

图7 IMF分项累计波动项位移预测结果Fig.7 Prediction results of cumulative fluctuation item displacement of IMF items
经计算得,CBSA模型波动项预测结果的拟合度R2为0.967 6,平均绝对百分误差MAPE为0.556 5,均方根误差RMSE为4.148 2,证明该模型预测精度较高。
4.5 对比验证
4.5.1 模型对比
为了进一步验证本文模型的准确性和优越性,分别建立CPSA、CBBA、CBS、BSA模型对滑坡位移波动项进行预测,其预测结果如图8所示。

图8 不同预测模型对波动项位移的预测效果Fig.8 Prediction results of fluctuation item displacement by different prediction models
分别计算各预测模型预测曲线的拟合度R2,平均绝对百分误差MAPE以及均方根误差RMSE,结果如表3所示。

表3 不同预测模型的预测精度比较Table 3 Comparison of prediction accuracy among different prediction models
由表3可知:
(1)CBSA较CPSA模型预测精度更高,说明在对SVR参数c、g进行优化时,BA较PSO算法具有更强的寻优能力,对SVR模型优化效果更为理想。
(2)与CBBA模型相比,CBSA模型预测结果的R2增加了19.32%,同时MAPE和RMSE分别减少了1.141 8和9.732 8。在对本文波动项位移样本进行预测时,与BP神经网络相比,SVR模型具有更高的适应性,模型误差在较大程度上有所降低。
(3)对比CBSA与CBS预测结果,发现经集成学习处理后的CBSA模型具有明显的预测优势,其各项评价指标值均较未经集成处理的模型更优,验证了集成学习对提高本文模型预测效果的有效性。
(4)将CBSA与BSA的预测结果进行对比发现,CEEMDAN分解后的位移序列具有更高的规律性,一定程度上降低了噪音及随机因素对预测效果的影响。因此经CEEMDAN处理后对各IMF分项进行单独预测,之后再将各分项预测位移相加得出累计预测位移的方法比直接对波动项位移进行预测的方法具有更高的预测精度。
综上所述,本文建立的预测模型CEEMDAN-BA-SVR-Adaboost在对白水河滑坡波动项位移进行预测时具有明显优势,预测效果较为理想。
4.5.2 案例对比
为进一步验证本文模型的适用性,采用CEEM DAN-BA-SVR-Adaboost模型对ZG118监测点波动项位移进行预测。分析确定影响因子的过程与ZG93监测点一致,计算得到各项间的灰色关联度均>0.6。因此,仍选用上述8个影响因子为预测模型输入数据集,预测结果如图9所示。

图9 ZG118监测点波动项位移预测结果Fig.9 Prediction result of fluctuation item displacement at ZG118 monitoring point
经计算,得出ZG118监测波动项位移预测结果的R2、MAPE、RMSE分别为0.966 3、0.288 6、4.924 5。预测位移曲线与实际曲线的拟合程度满足较高的预测精度要求,再次验证了本文提出模型的准确性及适用性。
4.6 总位移预测
将利用BP神经网络模型预测的趋势项位移与利用CEEMDAN-BA-SVR-Abdaboost模型预测的波动项位移相加得到最终滑坡累计位移预测结果,如图10所示。计算可得,模型累计位移预测结果的拟合度R2为0.970 2,平均绝对百分误差MAPE为0.002 1,均方根误差RMSE为5.953 4。发现预测结果的拟合度较单独预测波动项位移时高出0.26%,且误差也相对较小。这是由于趋势项位移的预测精度更优并中和了波动项预测的些许不足。

图10 滑坡累计总位移预测结果Fig.10 Prediction result of cumulative total displacement of landslide
结合上述CBSA模型与BSA模型的预测结果对比可知,机器学习在进行预测时,往往对更具规律性的数据序列预测效果更佳。在对其他无规律序列进行预测时,也可以借鉴此原理,对数据进行预处理,提取出其中具备物理或数学意义的子序列后再利用模型逐个预测,以此提高预测性能。
5 结 论
本文基于CEEMDAN、BA、SVR、Adaboost方法提出了一种基于CEEMDAN-BA-SVR-Adabo ost的滑坡位移预测模型,并将该模型应用到白水河滑坡位移变化的预测中,以此为基础,验证了该模型的准确性、优越性以及适用性,最终得出以下结论:
(1)依据对监测数据的分析及前人经验,结合案例初设8个影响滑坡位移变化的因子,分析这8个因子与ZG93监测点经CEEMDAN分解后的各IMF分项以及分项构成的波动项间的灰色关联度,其结果均>0.6,证明这8个影响因子为引起监测点波动项位移变化的有效因子。
(2)通过不同模型间的对比发现CEEMDAN-BA-SVR-Adaboost模型在对白水河滑坡位移进行预测时具有较高的优越性。CEEMDAN将位移序列彻底地分解为具有不同特定频率的子序列,预测模型在对此种序列进行预测时能够更好地发挥其预测性能。BA能够较好地对SVR中的参数进行寻优,在更大程度上克服了由于参数的随机性而造成的预测精度不佳问题。同时利用多个由BA优化过的SVR弱学习器组成的强学习器对滑坡位移进行预测,也从某种程度提高了模型预测的精确性。
(3)采用CEEMDAN-BA-SVR-Adaboost模型对ZG118监测点位移波动项进行预测,其预测结果的各项评价指标均证明该模型对滑坡位移预测具有较高的适用性,以此推断该方法可有效应用于对该滑坡其他位置处变形的预测。
本文模型仅适用于白水河滑坡等类土质库岸堆积滑坡,能否推广应用于其他类型的滑坡有待进一步考证。

