基于蚁群算法的分区拣货法的改进与实例研究
孟庆岩,王晶晶
(1.烟台黄金职业学院信息工程系,山东烟台 265400;2.烟台黄金职业学院机电工程系,山东烟台 265400)
互联网给电子商务带来了巨大的发展机遇,如何能在众多的电商中脱颖而出,除了产品的物美价廉外,还有非常重要的一个方面就是货物的高效送达,这就涉及到仓库的拣货与物流[1]。对于大多数的个体电商而言,货物运输选择高效的物流公司即可,而在仓库的拣货方面,则存在着很大的改善空间[2]。
传统的仓库的拣货方式分为两种,分别为单人拣货法与分区拣货法。所谓单人拣货法,即一张订单上所有商品的分拣都由一名拣货员完成,不管商品的种类及数量,这个拣货员可能需要经过整个拣货区进行拣货[3]。而分区拣货法[4],则是先把拣货工人分成与商品区数量相同的小组,各区的拣货员只负责分拣订单上该区的货物,当完成该区所有货物的分拣后,就把订单交到下个区的交接点。以此类推,订单依次经过所有商品区,最终完成分拣[5]。
文中基于网上超市订单拣货的方法问题,研究了分区拣货法的效率,并对分区拣货法加以改进与评估。
1 评价模型的建立
网上超市的分区拣货问题是一个实际问题,假设拣货区一共有m个分区,要求完成订单的顺序与发放订单的顺序完全一致,则在真实的工作环境中肯定会出现每张订单上所包括各类商品的比例不一样,而造成不同分区的工作量分配变化很大,从而造成工人的工作时间不同[6]。衡量一种拣货方法效率是否达到预期,标准是在某种工人配置下,其空闲时间占实际完成时间的比率,而比较不同拣货方法时,还要考虑不同方法完成相同订单所需的实际工作时间[7]。因此,通过横向与纵向两个方面对分区拣货法的效率进行了评价,而当引入工人人数的多少造成的拥挤度因子、工作的熟练度因子这两个因子时,模型得到了优化。
设在一定区域的拥挤度因子为C(N),工人熟悉自己所在分区货架的熟悉度因子为S(d),拥挤度与熟悉度影响的都是工人的单位时间工作量即工作效率,这里假设n名工人的最高工作效率为γk(k=1,2,…,n),则实际工作效率为:
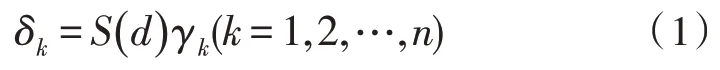
其中d为订单数。在一定分区内,工人一起进行工作,彼此之间肯定会产生影响,由于分区场地大小的限制,该分区内工人的人数越多,影响的程度就越大,拣货效率就会越低,即拥挤度因子的大小随着人数的增多而减小[8],因此得到不同分区的拣货效率为:
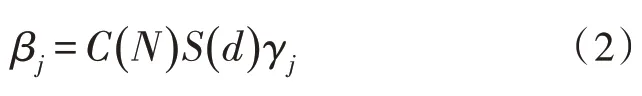
其中j为分区的数量,在本问题中的分区拣货法的分区数为j=m,而单人拣货法中j=1。
通过分析可知,熟练度因子S(d)随着时间的增长而增大,且增长率是先变大后变小,最终趋于1[9],这与种群增长的S 型曲线异曲同工,因此使用S 型曲线的表达式来表示熟练度因子为:
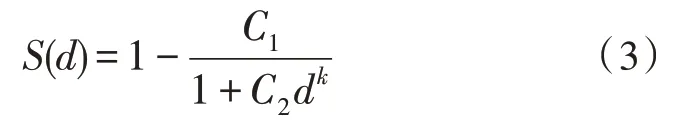
其中C1、C2是与d、k相关的常数,通过Matlab仿真实验,发现k=2 时,所得到的图像较为符合本题要求,令S(2 000)=1,即工作2 000 张订单后,工人的熟练度因子为1,因此得到熟练度因子的表达式为:
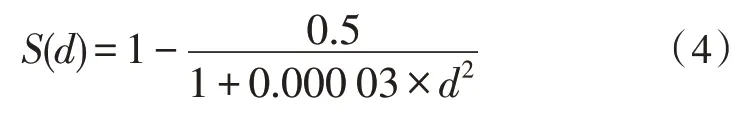
同理,拥挤度因子是随着时间的减小,其增长速度呈递减趋势,这与柯西分布隶属度函数较为相似,因此使用柯西分布隶属度函数来表达拥挤度:
通过Matlab 仿真实验发现,当k=0.8 时所得到的图像较为符合要求,我们令C(n)=0.5,即工人数为15 时,拥挤度为0.5,得到拥挤度因子的表达式为:
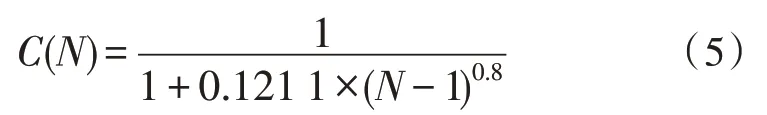
由于工人的拣货效率是不同的,且要求完成订单的顺序与发放订单的顺序完全一致,而拣货区共有m个,这就造成了每个分区的拣货效率是不同的,假设每个分区的工作效率βj为每个分区的拣货效率,则。现假设一批订单到达该网上超市,第一张订单发放时刻为t0,设αij为第i张订单在第j分区的数量,tij为第j分区完成第i张订单的时刻距离t0的时间,故有:

下面来求每个分区的空闲时间,设每个分区的空闲时间为tj,由于第一分区每完成一张订单就执行下一张订单,故其空闲时间为:

而对于第j分区,当i=1 时,分别要等待t1,j-1,当i>1,若第i-1 张订单已完成而第i张订单还没到,则需等待ti,j-1-ti-1,j,反之则不需等待[10]。
综上所述,各分区的空闲时间为上述每张订单等待时间之和:

设ηj为第j分区的工作效率,η为总效率,则:

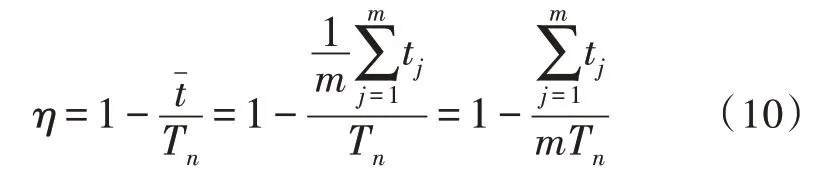
2 评价模型求解
令m=5,n=15,当每个分区的拣货效率均衡时,对于随机产生的五批订单,每批订单有100 张,求其总效率以及各分区的效率,并相互比较。通过LINGO 编程,得到如表1 所示分组。

表1 分区人员情况
此时,每个分区的拥挤度相同都为C(3),得到结果如表2、表3 所示。
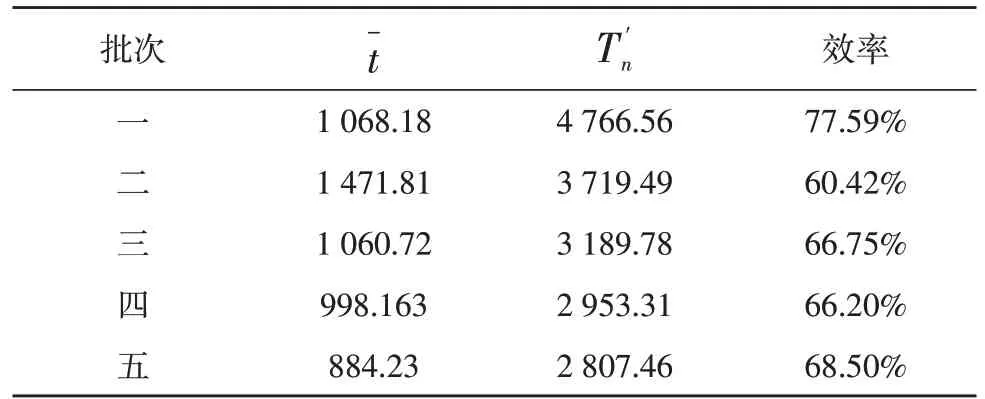
表2 拥挤度结果
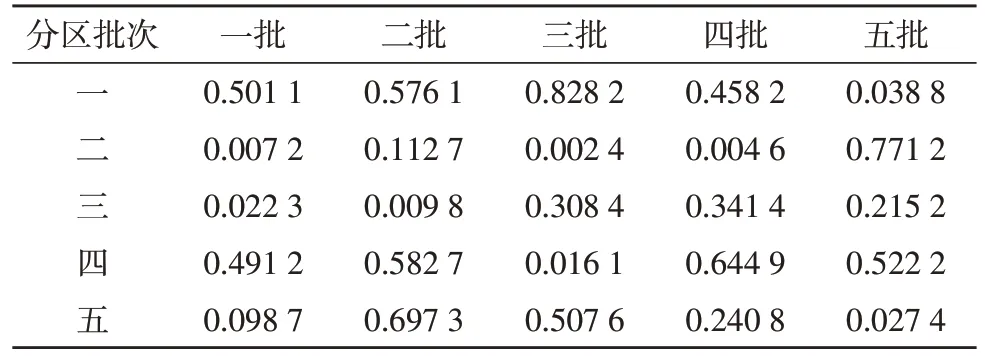
表3 各分区的效率情况
在熟练度因子与拥挤度因子的作用下,发现分区拣货法与单人拣货法的完成时间有很大的差距,分区拣货法的完成时间明显低于单人拣货法。
在单人拣货法中,每个人的空闲时间少,但是完成时间却较长,这是由于单人拣货法每个人要熟悉50 个货架所有的摆放位置,而且15 个人同时在拣货通道里进行工作,给拣货造成了一定的影响。而分区拣货法通过分区使得拣货通道的各段都得到利用,同时每个人只需熟悉10 个货架,提高了拣货效率,因此分区拣货法的拣货效率要明显高于单人拣货法,但由于其均衡配置使得分区拣货法也存在着很高的改进空间[11]。
3 不均衡配置下的分区拣货法
实际生活中,各类商品的需求是不一致的,为了使模型更加贴近实际,具有可操作性,选取5 个分区:食品区、饮料区、日用品区、电器区与礼品区。通过查找资料,得到5 类商品的生活实际购买需求占比分别为:食品区占22.99%;饮料区占5.75%;日用品区占43.10%;电器区占17.53%;礼品区占10.63%[12]。
同样取m=5,n=15,每个分区的工作人员都为3 人,建立比例分配模型。通过统计网上超市的订单中各类商品的数量,得到各类商品的数量比例为wj,则当各个的拣货效率按该比例分配时得到每个分区的实际拣货效率为:

其中,S(d)与订单的数量有关,而在按订单比例分配拣货效率的时候,S(d)也是按订单比例增长的,所以S(d) 对开始进行的人员分配不影响。Cj(N)=S(3),每个工人的理想拣货效率为从而实际拣货效率为:

当vj已知时,也已知。
在每个分区限制3人,每名工人的拣货效率为1-15,共5个分区的约束条件下,建立优化模型如下:
引入0,1 变量,

设Ej为实际的各分区最终效率,建立如下优化模型:
目标函数:
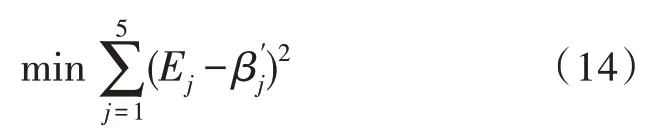
约束条件:

利用之前的评价模型可得到的效率为η1。
使用查找的实际商品数量比例数据,利用建立的按比例分配模型与均衡配置模型作对比可以得出,按比例分配模型的效率远高于均衡配置模型,证明这种改进方法是值得提倡且具有实际应用价值[13]。
4 基于蚁群算法的分区拣货模型
分区拣货法使得拣货员限制在相对封闭区域工作,在此拣货系统中的拣货员会越发熟悉自己负责区域里的产品,这样不仅可以提高拣货效率,也提高了作业准确性。然而,在实际中,由于各分区工作量难以达到均衡,经常出现当某一分区拣货员回到上一个交接点时,由于前一分区还没有已完成订单,但又不能越过交接点去帮忙,只能无奈的等待[14]。这给人员和设备的利用率造成很大的浪费,也导致传统网上超市分区拣货中各分区的空闲度差异较大,整体效率不高。为此,我们放松区域限制,采用蚂蚁拣货法对分区拣货法进行改进。
4.1 蚂蚁拣货法及其假设
在蚂蚁拣货法中,15 名工人在拣货流水线上来回作业。按照工人所在流水线位置由上游到下游的顺序,分别把工人编号为:1、2、……15。他们的拣货效率分别为γj,按照货架所在流水线位置由上游到下游的,分别把货架编号为:1、2、……50。n(n>1) 张订单每种货物拣货量矩阵A=(Aij)n×50。
该文在以下假设下计算蚂蚁拣货法的时间:
假设一:工人在货架上走动的时间可以忽略。
假设二:工人j与工人j+1 在货架k交接时,无论工人在本货架的拣货作业是否完成,都立刻把订单交给下一工人,若货架k的拣货作业未完成,则由工人j+1 完成。
假设三:订单交接的时间忽略不计。
假设四:在拣货过程中工人j在流水线上的位置不可能超过j+1,最多两者在同一货架。
注:工人j手中订单需要拣的货物较少时,赶上了下游正在拣货的j+1 工人,俗称“追尾”。此时不能超越j+1 工人,直到j+1 工人掉头才能将订单及拣货筐转交给j+1 工人。
4.2 蚂蚁拣货法的完成时间
首先要安排15 名工人在流水线上的初始位置,显然工人1 从办公室拿到订单从货架1 开始拣货,其初始位置即为货架1。而其他工人的初始位置则依次安排在货架5、8、11、15、18、21、25、28、31、35、38、41、45、48。
对于订单1,由假设一和三可知,工人1 从开始执行订单1 到把订单交给工人2 所花的时间仅仅用在拣货上,即工人1 执行订单1 的时间t1,则执行订单1 共用时:
对于订单2,由于工人1 把订单1 交给工人2 后马上返回办公室拿订单2,并且根据假设一,可以认为工人2 执行订单1 与工人1 执行订单2 是同时开始的。而t2时间后,工人2 将订单1 交给工人3,马上返回从工人1 接过订单2,再由假设一,可认为工人1执行订单2 的时间也是t2。同理可知:工人j(2 ≤j≤14)执行订单2 的时间分别为:t3,t4,…,t15,而工人15 执行订单2 的时间则单独记为:t16。则执行订单2 一共用时:
考虑到订单2 是在订单1 执行t1时间后与订单1同时执行,故执行者两张订单的时间T总2应该为T1与T2之和减去重叠的时间,即:
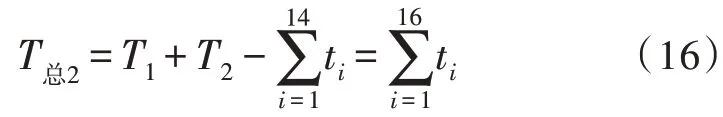
以此类推,执行n张订单的时间为
设a=(aij)n×15表示在执行订单i工人j与工人j-1 交接时,工人j-1 在交接货架上未完成的拣货量,对于j=1,则默认ai1=0,i=2,3,…,n,对于订单1,认为a1j=0,j=1,2,…,15。
gup=(gupij)n×15表示在执行订单i时,工人j与上游交接时所在的货架编号,其中,认为gup1,2=4,gup1,3=7,…,gup1,15=47,gupi1=0,i=1,2,...,n。
gdown=(gdownij)n×15表示在执行订单i时,工人j与下游交接时所在的货架编号,其中认为gdown11=4,gdown12=7,gdown13=10,...,gdown1,14=47,gdowni,15=50,i=1,2,…,n。显 然 有gdownij=gupi,j+1,i=1,2,…,n,j=1,2,…,14。
下面讨论如何求t16,t17,…,tn+14:
考虑执行订单i过程中工人j和j+1 的交接情景,由假设四可知,只有两种可能:

Case1 说明工人j从工人j-1 手中接过订单i时所在货架与工人j+1 将订单i-1 交给工人j+2时所在货架是同一货架,此时工人j立刻把订单给工人j+1,则有:

而在Case2 中,则需要考虑在工人j执行订单i的时间ti+j-1内是否会追上工人j+1,此时亦有两种可能,即:
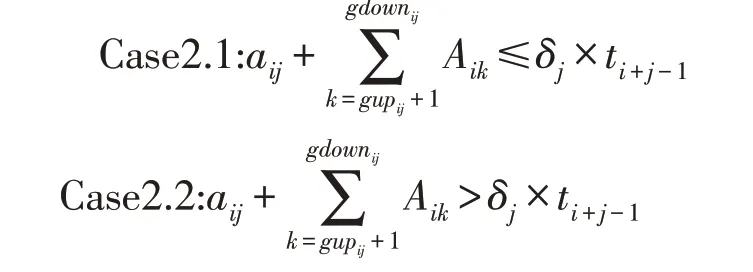
在Case2.1 中,在ti+j-1时间内,工人j会追上工人j+1,由假设四,工人j不能继续往下拣货,只能跟在工人j+1 的后面,当工人j+1 在货架gdowni-1,j+1完成订单i-1 时,工人j再把订单i给工人j+1,故有gupi,j+1=gdowni-1,j+1,ai,j+1=0。
在Case2.2 中,在ti+j-1时间内,工人j追不上工人j+1,他们会在货架k交接(货架k在货架gupij与gdowni-1,j+1之间,k的求法将在图1 中给出),故有:
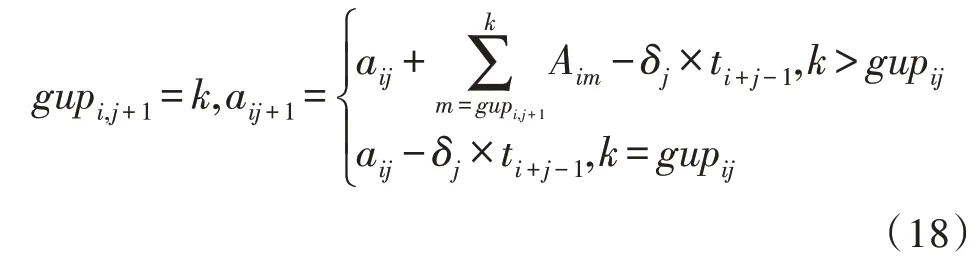
综上所述,可以得到:
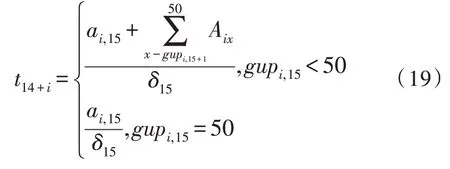
4.3 蚂蚁拣货法的空闲时间
记rest(restij)n×15为工人的空闲时间矩阵,其中restij表示在订单i中,工人j的空闲时间[15]。
对于订单1,显然工人1 的空闲时间为0,即rest11=0。而工人j(j>1)的空闲时间产生即为工人1开始执行订单1 的时刻开始,到工人j从工人j-1手上接过订单的这段时间,故:

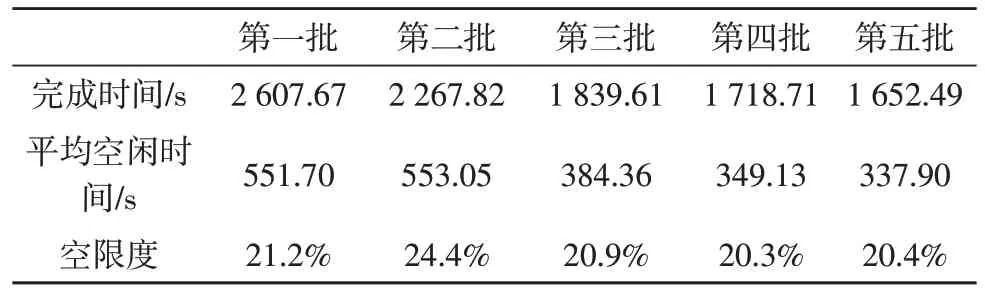
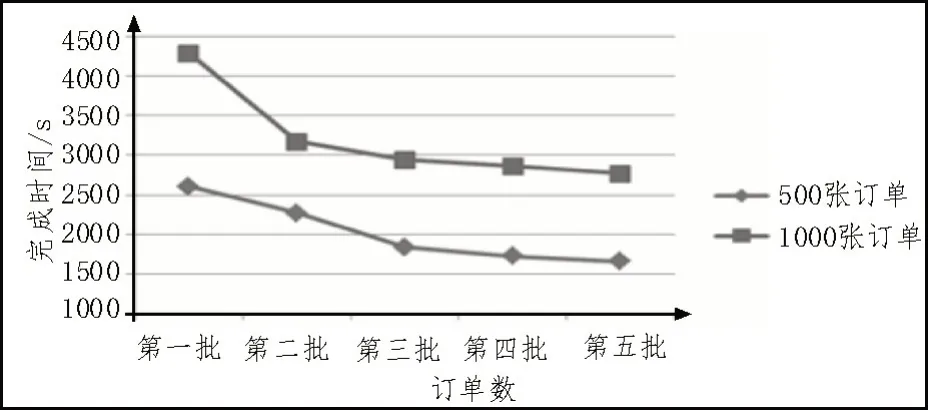
对于订单i(1 在Case1 中,空闲时间为工人j+1 完成订单i-1的时间,故restij=ti+j-1。 在Case2.1 中,在工人j(j<15) 执行订单i的时间里,本应完成拣货量δj×ti+j-1,却因不能超过工人j+1 而只能在完成拣货量之后进入空闲状态,等待工人j+1 完成订单i-1,故: 对于订单n,工人j的空闲时间除了在HOTO(i,j)过程中产生外,还产生在交出订单n后等待后面的工人把订单n完成的时间段,前者记为ttj,后者记为tt′j。ttj的计算方法前面已给出,而,故: 由此可以计算每个人的总空闲时间: 4.4.1 蚂蚁拣货的算法实现及流程 在4.3 中已解决执行订单i过程中工人j与j+1交接的问题,称解决该问题的上述过程为HOTO(i,j)过程[16-17],其中i表示订单号,j表示工人j和工人j+1 交接,该算法流程如图1 所示。 图1 算法流程图 有了HOTO(i,j)过程,就可以求t16,t17,…,tn+14,从而可以计算得到与总空闲时间 4.4.2 蚂蚁拣货法的结果 通过以上的蚂蚁拣货算法,我们采用不均衡配置模型中按比例生成的订单,得到在该模型的基础上的完成时间及平均空闲时间,如表4 所示。 表4 蚂蚁拣货法的完成时间及空闲 从表4 发现蚂蚁拣货法的空闲度相对比较大,这是由于在该拣货法中,第一名工人在进行第一张订单的拣货时,其他14 名工人都处于空闲状态,这就造成了相当大的空闲时间,均衡配置下的分区拣货法完成时间最长,其次为按比例分配的分区拣货法,最后为蚂蚁拣货法,这说明我们利用蚂蚁拣货法比分区拣货法的效率高,完成时间短,这是一种较好的拣货法。 蚂蚁拣货法可以充分利用每个工人的拣货效率,比按比例分配法的效率明显提高,使用这种方法可以不需要频繁调动工人工作分区,提高拣货效率。图2中增加了订单数,使得5批订单每批订单都有200张。从图中可以看出,随着订单数的增加,蚂蚁拣货法的效率也会增长,到达收敛值时增长比较缓慢,但是利用蚂蚁拣货法完成同样数目的订单时间明显会越来越短。 图2 不同数目订单完成时间 采用蚂蚁拣货法过程中,优化了拣货员的排序,但是依然不可避免地出现部分“追尾”现象,如果在订单期限允许范围内能对订单的顺序做进一步优化排序,进一步减少“追尾”,则所得的结果会更理想,这是该模型的不足之处。最后,拣货问题是物流业中的重要研究课题,建立的模型能更好地接近实际问题,实用性就越强。在该问题给出的条件中,忽略了工人在各货架或分区间走动的距离,简化了问题。如果将工人行走距离、工人和设备的成本、订单期限、作业准确率和顾客满意度等考虑进去,建立基于成本分析的优化模型,会使模型更具实用性。

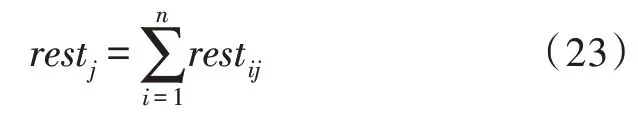
4.4 模型的求解

5 结果分析
6 结论

