面向个性化继续教育的关联规则挖掘算法研究
胡 悦,罗小楠,王 彬,张 伟
(空军军医大学教学考评中心,陕西西安 710032)
近年来,随着社会教育水平的不断提高,继续教育的需求逐年增加[1]。利用互联网发展的红利,实现互联网+继续教育的模式是继续教育行业的一个新的趋势[2-3]。为了更优地提高继续教育的教学水平,满足不同人群的需要,面向个性化继续教育研究新方法成为一个研究热点。在个性化推荐方面,关联规则挖掘算法在诸多领域均得到了应用[4-6]。文献[7]提出利用关联规则算法,实现高校图书馆书籍个性化推荐。文献[8]利用学生信息进行关联规则挖掘,在教育管理系统上实现了个性化管理。相似的,文献[9-10]分别利用关联规则模型建立了银行产品个性化推荐模型和医疗用品推荐模型。这些研究和应用在一定程度上说明了关联规则算法可以实现个性化的方案推荐,能够挖掘数据间的关联关系。
为了进一步提高关联规则算法的性能,针对算法的改进也得到了广泛的研究[11-12]。文献[13]基于MapReduce 计算模型对关联规则算法改进进行了总结。针对基于关联规则的数据挖掘方法,文献[14-15]分别提出利用模糊逻辑规则和聚类方法提高关联规则挖掘的算法性能。此类算法改进在较大程度上可以提高关联规则挖掘的准确性,为个性化推荐提供依据,但在非确定性属性关联情况下仍需研究新的方法[16]。
该文面向个性化继续教育方案优化的需求,研究了关联规则挖掘算法。在构建个性化继续教育方案的基础上,文中利用关联规则算法,通过建立强关联规则和频繁项集,实现数据属性的关联规则挖掘。为了获得更准确的强关联规则,该文利用DBSCAN 聚类算法进行不确定聚类数目的自适应规则聚类。通过仿真试验与数据分析,说明所提算法相对于现有算法规则聚类结果更加合理,在个性化继续教育方案优化方面,具有更高的实用性。
1 系统模型
继续教育个性化是目前的发展趋势,为了满足大规模用户人群的个性化继续教育的需求,文中提出基于关联规则挖掘算法的个性化继续教育优化方案。其可以有效挖掘不同用户群体的需求与期望,根据用户自身情况进行个性化教育优化,方案架构设计如图1 所示。
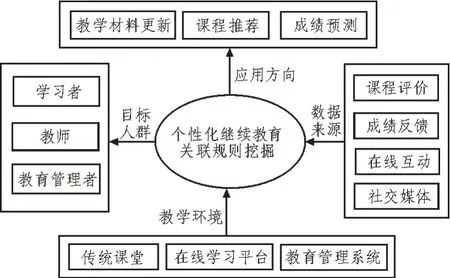
图1 个性化继续教育方案架构
文中设计的基于关联规则挖掘的个性化教育方案架构主要分为目标人群、应用方向、教学环境和数据来源4 部分。
1)目标人群。个性化教育方案的目标人群主要包括学习者、教师和教育管理者3 种,教育管理者与教师根据个性化数据挖掘为学习者制定个性化教育方案;
2)应用方向。个性化教育主要可以应用于教材更新、个性化课程制定推荐和学生成绩预测等,针对学生的个人情况和课程匹配程度制定学习方案;
3)教学环境。除了在传统课堂教学环境上进行应用,个性化教育还可以应用于线上教育平台和教育管理系统;
4)数据来源。进行个性化继续教育数据挖掘,需要保证数据的充分性和多样性,数据来源主要包括课程评价、学生成绩反馈、师生在线互动以及社交媒体上的评价,通过多种渠道确保数据的多元性。
2 算法架构
文中提出的面向个性化继续教育的关联规则挖掘算法的架构如图2 所示。算法流程分为数据库准备、数据预处理、关联规则建立、产生频繁项集和关联数据挖掘5 部分。

图2 关联规则挖掘算法架构
基于关联规则的数据挖掘,首先需要建立挖掘数据库,将需要挖掘的数据放入数据库中。在准备好原始数据后,需要进行数据预处理。预处理内部如图3 所示,数据预处理的效果在较大程度上影响算法的挖掘效果和运行效率。
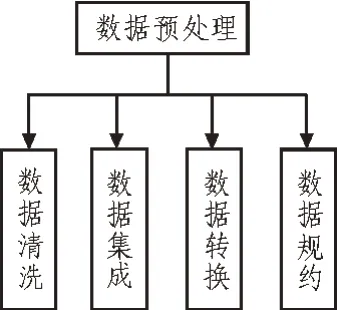
图3 数据预处理架构
建立关联规则是算法的核心,在若干可组合规则中选择具有最大影响的核心规则,可保证数据挖掘结果的有效性。与关联规则有直接关系的是频繁项集,两者是互偶关系。在若干属性中确定最频繁出现和结果关系最大的属性,才能建立正确的关联规则。确定完两者后,即可对预处理后的数据进行数据挖掘。如图3 所示,数据预处理架构主要包括数据清洗、数据集成、数据转换和数据规约4 部分。
3 个性化关联规则挖掘
面向个性化教育的数据挖掘算法设计,首先需要建立关联规则。其是指由事件X必然可以导致事件Y的发生,事件Y是事件X的结果,事件X是事件Y的原因,即X⇒Y。
假设所有预处理后的数据集合为D,事件X⊆D,事件Y⊆D,且X⋂Y=φ。若有X⇒Y,则事件X与事件Y之间存在关联规则。
关联规则可分为强关联规则和弱关联规则,根据规则的支持度和置信度来进行划分。关联规则的支持度是指同时包含集合X和集合Y的事件数量与数据集合中D事件总数之比:
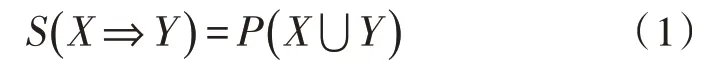
置信度是指集合中同时包含集合X和集合Y的事件数量与包含集合X的事件数量之比:
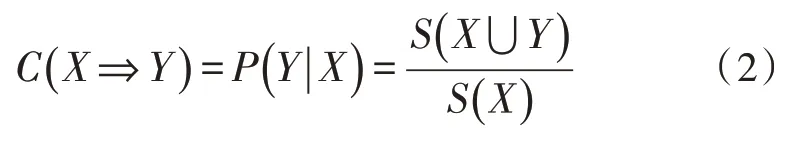
设最小支持度与最小置信度为Smin和Cmin,若规则的支持度与置信度可以同时大于最小支持度和最小置信度,则此规则为强关联规则;否则,为弱关联规则。
为了制定个性化的继续教育方案,需要对数据进行分类,文中提出基于聚类算法对数据间的关联规则进行分类。数据集合中的数据由事件、事件子集和关联规则等元素组成,对数据进行聚类,需要计算集合元素间的距离。
设数据库中任意两个事件I1和I2,其中I1∈X,I2∈Y,则I1与I2之间的距离定为:
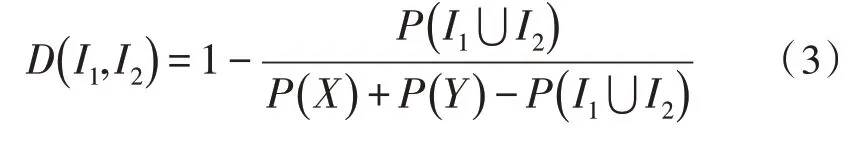
事件之间的距离定为两个事件同时发生的次数占所有包含I1或I2的事件数目之比,其取值范围为0~1,即两个事件总是同时发生,其距离为0;两个事件完全无法同时发生,则其距离为1。
设事件集合X与Y分别包含m和n个元素,则两个事件集合的距离定义为集合内所有元素的平均距离,即:

事件集合之间的距离范围为0~1。
关联规则之间的距离定义较为抽象,设数据库存在规则r1和r2,其规则定义可表示为:
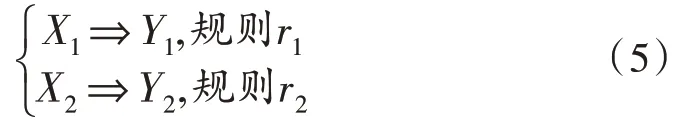
则r1与r2之间的距离可定义为:
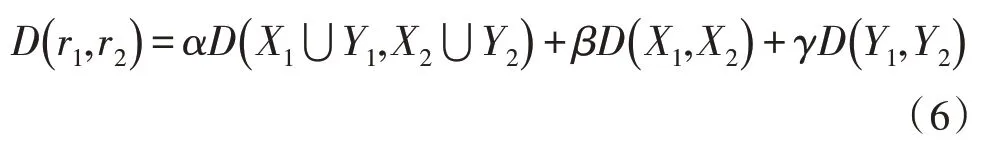
其中,α、β和γ是自定义调节参数,可根据实际数据情况进行调节,对参数进行归一化处理:
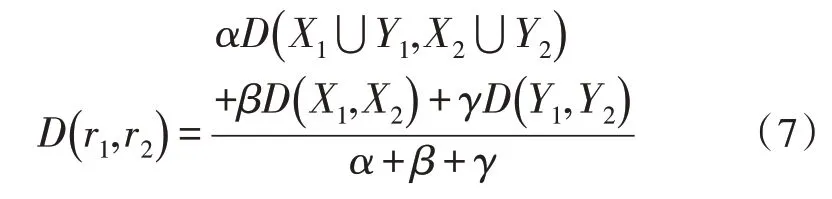
为了简便分析,一般使自定义调节参数之和为1,α+β+γ=1。
随着计算机技术的不断发展与完善,计算机病毒问题也变得越来越棘手。计算机病毒的防范是一个综合的系统工程,它主要包括了对单个计算机系统与整个网络的病毒防范过程。如果想要对整个计算机网络进行防范就必须要进行统一的管理,首先必须要使用统一的网络病毒查找软件,这个软件能够及时准确地对网络中的病毒进行识别并及时的做出相应的处理。第二,网络杀毒软件要对整个网络进行杀毒处理,这些软件也要能够在没有人工干涉的条件下自动升级,自动对病毒进行深层次的消毒处理,保证网络系统的安全性与稳定性。
为了实现关联规则挖掘,文中提出利用DBSCAN 聚类算法进行分类,并使用轮廓系数来评估聚类算法的性能,轮廓系数的定义为:

其中,ai表示样本i到同一规则集合其他样本的平均距离,bi表示样本i到其他任一规则集合样本的平均距离。式(8)可以改写为:
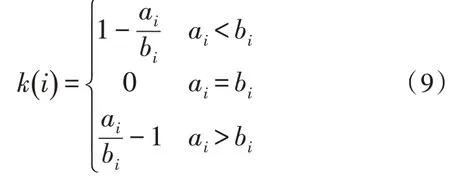
由式(9)可知,轮廓系数取值范围为-1~1。轮廓系数越接近于1,说明该样本属于该规则集合的概率越大;轮廓系数越接近于-1,说明该样本属于该规则集合的概率越小。当轮廓系数为0 时,该样本属于两个规则集合的概率相等。
文中提出的DBSCAN 聚类算法流程,如图4 所示。其中,可达规则密度是指在规则可达半径内的样本数目。
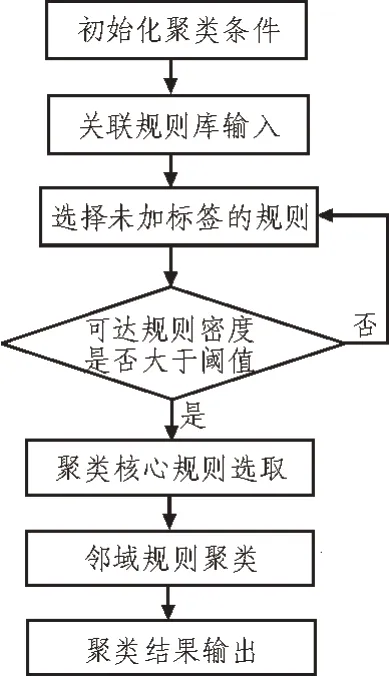
图4 DBSCAN聚类算法流程图
面向个性化继续教育的需求,文中设计了基于DBSCAN 聚类的关联规则挖掘算法,其步骤如下:
1)输入:数据集合g,最小聚类数目Nmin,可达密度阈值e;
2)随机确定聚类中心Ci;
4)将元素i从数据集合g中剔除;
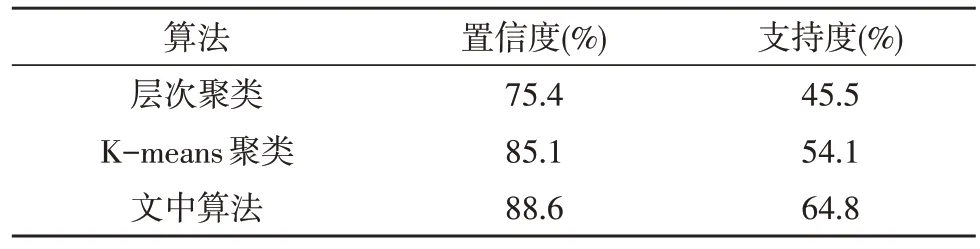
5)若N(Ri) 6)计算集合中元素j到聚类中心的距离εij; 7)若εij≥e,则继续执行步骤8);否则转到步骤9); 8)将元素j加入到关联集合Ri; 9)将元素j从数据集合g中剔除; 10)j=j+1; 11)生成若干个数据类别集合{Ri}; 12)输出:数据类别集合{Ri}。 为了验证所提的面向个性化继续教育的关联规则挖掘算法的有效性,文中通过对比现有算法与所提算法的聚类轮廓系数,比较聚类算法的合理性。另外,通过分析对比不同聚类算法下的关联规则置信度和支持度,说明了所提算法的有效性。 如表1 所示,该文在5 个不同数据集上进行关联数据挖掘,对比层次聚类算法、K-means 聚类算法和文中所提的DBSCAN 聚类算法的聚类轮廓系数。整体上看,K-means 聚类算法略优于层次聚类算法。但在部分情况下,由于K-means 聚类算法的聚类中心数目错误,导致其性能反而低于层次聚类算法。文中所提算法在不同数据集合上的轮廓系数均高于其他两种算法,说明聚类结果更合理。 表1 不同算法聚类轮廓系数对比 如表2 所示,在同一数据集下,该文对比了基于3 种聚类算法的关联规则挖掘算法的置信度和支持度。文中所提算法的关联规则置信度与支持度均高于层次聚类算法和K-means 聚类算法,说明文中所挖掘的关联规则属于强规则,利用所挖掘的规则可以更智能地进行个性化继续教育方案优化推荐。 表2 不同算法关联规则置信度和支持度对比 为了满足个性化继续教育方案优化的需求,基于关联规则挖掘算法提出了一种智能的个性化继续教育方案制定技术。利用DBSCAN 聚类算法实现数据集内聚类中心数目不确定情况下的自适应聚类,并根据聚类结果提取核心规则进行个性化继续教育方案优化。通过仿真分析证明,所提算法相对于现有聚类算法,聚类结果更合理,且具有较高的鲁棒性,而且该算法可以挖掘的规则关联性更强,在继续教育方案优化领域具有良好的实际应用价值。4 仿真验证及数据分析

5 结束语

