探讨几何画板在数学整理复习中的辅助作用*

魏明宏

马鞍山市金瑞小学 安徽 马鞍山 243000

引言

小学数学《义务教育数学课程标准》中指出：数学课程的整体设计应充分考虑现代信息技术的整合与应用基于信息技术丰富数学学习内容，开发适合学生数学学习的资源，应用信息技术优化教师教学和学生学习的手段，把信息技术作为教师教学的实用载体，突破原有教育环境的约束，建立更为开放多元的师生、生生关系，激发学生的学习兴趣，使学生乐意并有可能投入到现实的、探索性的数学活动中去。

下面以多媒体工具几何画板在小学数学《平面图形的面积整理复习》课为例，来说说我是怎么利用信息技术为载体来提高课堂效率，较好地把学生引入思考、探索、创新的情景之中，使学生亲身体验“做数学”的快乐。

1 在点线运动中了解知识来龙去脉

六年级学生已了解面积与物体表面大小的联系，复习课开始导入是从学生薄弱的几何知识的角度导入，通过点动成线，线动成面的转化，让学生体验平面图形知识之间的联系，让学生了解知识的来龙去脉，形成知识的网络体系。

点和线，线和面看似是极其简单，要说清关系却不容易。关键在于这个"动"，如何动？如何描述才能让学生更深刻地理解。单纯靠讲，把一种抽象转化成另一种抽象是比较费劲的。基于几何画板，能够直观地展示点线运动的轨迹，揭示点与线、线与面之间的关系，让学生亲眼感受到线是由无数个点组成，面由无数条线组成，而且它们不同的运动方式产生不同的线与面。从而把点线面的关系清晰完整地展示出来[1]。

2 在边线的运动中清晰平面图形间的内在联系

整理复习课的一个重要特点就是要构建知识间的网络，新课往往是单个知识点学习，而整理复习课教学时，恰恰可以在学生基础知识点上，引导学生在各知识点之间寻找联系，通过整理复习，构建一个具有内在联系知识网络体系，达到知识和思维的融会贯通。下面以《平面图形整理复习》为例来说说如何利用多媒体课件来展示平面图形之间的内在联系的。

平面图形整理复习前测问题：①你认为平面图形之间有什么联系？②你能说说有曲线组成的圆和直线组成多边形的区别和联系吗?

首先，引导学生课前去思考、探索、分析与整理，在让学生把整理好的思路在复习课上充分交流、展示后，老师通过几何画板课件动态演示学生思考的过程，形象地展现出平面图形之间联系，使零碎的平面图形的面积知识统一于梯形面积公式之中，提高学生的学习效率，同时培养学生发现问题、分析问题解决问题的能力。

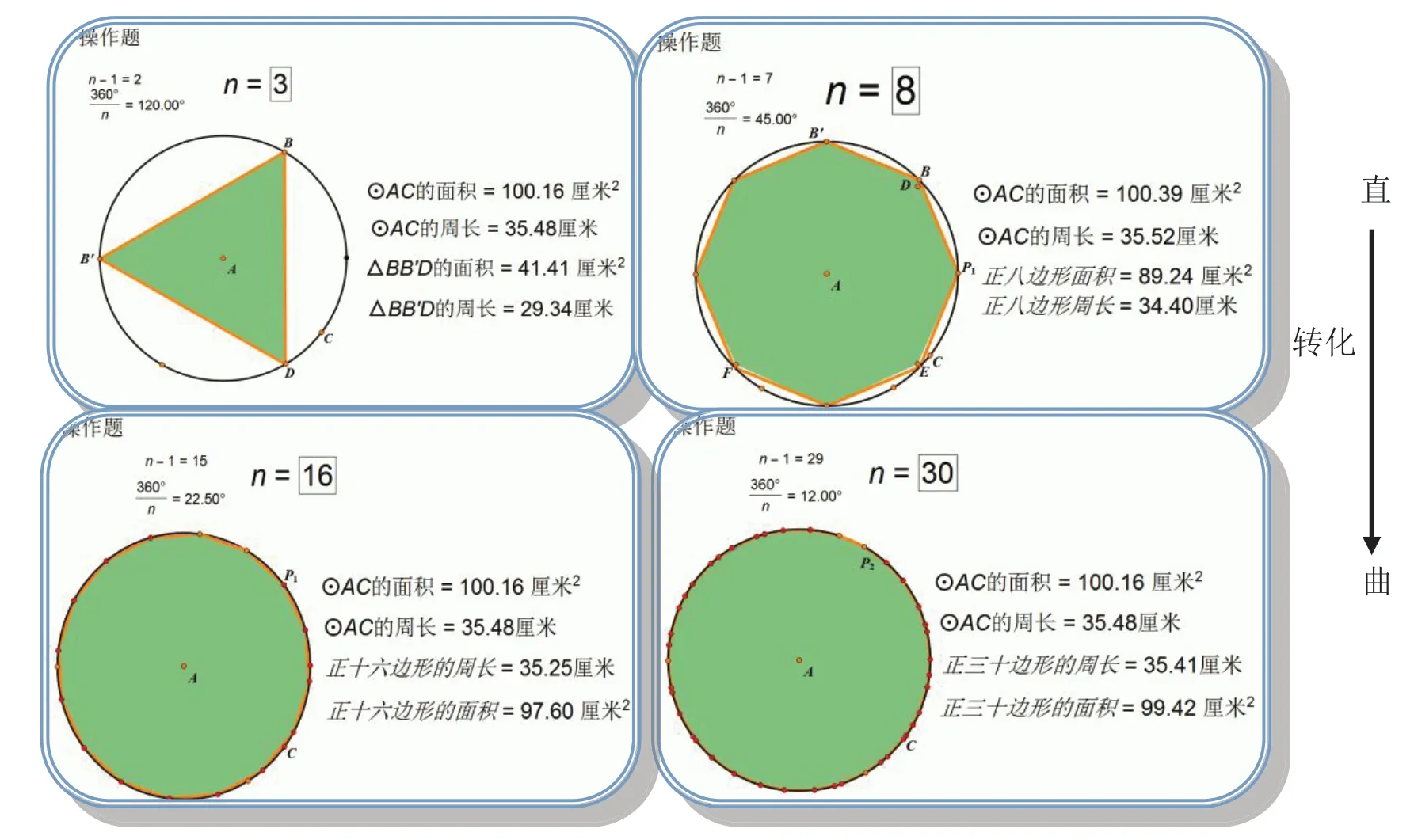
图1 正多边形向圆转化

当梯形上底改变的（高和下底不变）时候，就会由一种图形转变成另一种图形，这种变化可以借助几何画板来轻松实现，接着，教师提问：“既然不同的四边形之间有着密切的联系，那么它们面积公式之间有什么联系呢？”

让学生分小组讨论、交流、探究。学生通过以上几何画板的动态演示，很快就发现面积公式之间的联系。

然后，教师又提问：直线围成的平面图形之间（长方形、正方形、平行四边形、三角形、梯形）有密切联系，那么它们和圆有联系吗？

虽然课前让学生进行预习，但是此题对于学生来说既抽象又陌生，能回答出正确结果的人很少，教师通过几何画板的迭代，边演示边启发，学生边观察边猜想，随着正多边形的边由少到多，逐渐地线由直变曲，图形由方变圆。（如图1）课件演示。

在一个圆内画一个内接正三角形，随着单击次数的增加，圆不变，其内接图形从正三角形变化为正四边形、正五边形、正六边形，一直到正十边形、正二十边形，等等。在这一过程中，可以引导学生观察圆内空白部分的变化情况，感受到正多边形随着边数的增加，不断向其外切圆逼近，从极限思想上看，就逼近成一个圆。

几何画板把这种小学难以想象和体验的思想“入微”地展现在学生的眼前，学生惊奇、兴奋地感受到正多边形随着边数的增加，不断向其外切圆逼近，多边形的周长和面积不断地向圆的周长和面积逼近[2]。

3 在图形运动中，突破重难点。

复习的目的之一是查缺补漏，使学生融贯通地掌握已学的内容。因此在选择范例时要尽量针对本章节知识重难点，正视学生的起点，有的放矢，提高数学课堂效率。

（如图2图①）课件演示。

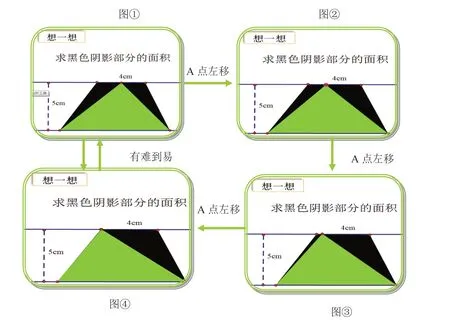
图2 三角形等积变化

此题，全班53名学生，正确答案是28名，能说清道理不过16名。主要是对两个黑色三角形的底是未知数不能理解，认为缺少已知条件不能计算，能得出正确答案的学生，一部分用特例法（把a点作为中间点，两个黑色三角形底都是2cm计算的）计算的。还有一部分成绩较优秀学生认为：两个黑色三角形等高，两个底之和是4厘米，所以用5×4÷2=10平方厘米得出结果。可是当老师问到为什么可以把两个黑色三角形底的和理解为是4厘米，高是5厘米作一个三角形计算时，学生却认为两个黑色三角形边不相等无法合并成一个大三角形。只有一个同学认为可以用等底等高的三角形面积变换解决这个问题。教师让这位学生上讲台，亲手把绿色三角形的顶点向左移动(如下图①-②-③-④)，最终两个黑色三角形合并成一个黑色的三角形，此时很多学生豁然开朗。

教师选择这道平时学生错误率高、难理解，有着丰富变化的多边形例题。目的是通过考查学生对平面图形的“高”的掌握程度。“高”是小学生学习平面图形面积的最大难点，而“高”的本质是否理解又直接影响平面图形的面积计算。可是通过几何画板简单地顶点移动，就直观地展现出等底等高红色三角形的等积变化，这对于学生理解“高”有着很大帮助，为难点突破起到了很好的辅助作用。

几何画板不是万能的，虽然几何画板功能强大，但是教学要以服务数学教学为目标。不要以教学预设时做好的课件为教学线索，按部就班地播放，而是应该以课堂上学生即时生成的学习状况为依据选择使用合适的课件。不要让“计算机”抢了“学生的戏”，处理好计算机速度“快”与学生学习思考“慢”之间的关系。计算机的辅助不是替代学生的思考，而是帮助学生更好地思考。

以上这些，就是我在应用几何画板辅助小学数学《平面图形复习整理复习》中的一些想法，和大家交流一下。