直流偏磁对二次谐波制动判据的影响及对策
陈争光 ,刘一民 ,王兴国 ,郑少明 ,李春波 ,邓丽虹
(1.中国电力科学研究院有限公司,北京 100192;2.电网安全与节能国家重点实验室,北京 100192;3.国家电网有限公司华北分部,北京 100053;4.天津大学智能电网教育部重点实验室,天津大学电气自动化与信息工程学院,天津 300072;5.北京交通大学,北京 100053)
在单极-大地运行模式下,包括柔性直流输电在内的高压直流输电系统会引起接地极周围一定范围内大地电位的升高,造成附近交流系统不同接地点之间出现电位差[1-4]。这一电位差会在交流变压器和输电线路之间形成直流回路,在变压器内部产生直流磁通和大量谐波,即变压器的直流偏磁现象,影响系统的安全运行[5]。
变压器直流偏磁会对其保护产生影响。主要体现在直流偏磁产生的大量二次谐波会引起变压器差动保护二次谐波制动判据的误启动上。目前这一问题已经引起业内的广泛关注并开展了大量研究。文献[6]根据有限元原理以变压器实际参数为基础建立了场路耦合模型,根据自耦变压器高中压绕组电气连接特点,仿真分析了偏磁直流电流的大小对750 kV自耦变压器励磁电流和内部磁场分布的影响;文献[7]研究了电流互感器起始饱和时间受直流偏磁的影响,并分析了电流互感器局部暂态饱和对变压器差动保护的影响,研究结果表明直流偏磁可能会加速电流互感器饱和,进而可能引起变压器差动保护的误动;文献[4]针对三相五柱变压器的直流偏磁问题,利用麦克斯韦方程代替铁心柱的磁路方程与电路进行耦合,结合铁心的非线性特征曲线对三相五柱变压器直流偏磁特性进行了理论研究;文献[8]通过分析有无直流偏磁下变压器区外故障及故障切除后差动保护的动作情况,验证了直流偏磁对故障后CT饱和速度和饱和程度的加速作用。基于分区信号设置了差动保护比率制动特性的延时动作区,通过提高比率制动特性的最小动作电流,避免了差动保护的误动;文献[9]通过仿真研究了直流偏磁对电流互感器和变压器的影响,针对处于直流偏磁下的电力变压器,提出了一种基于正弦波数列特性的电流互感器饱和识别方法,同时提出了基于PWM波形特征和变压器差动电流偏度系数的励磁涌流识别方法,并对以上方法进行了验证。现有研究中多是研究直流偏磁对变压器励磁电流和传变特性的影响以及直流偏磁通过影响CT对保护产生的影响,而直流偏磁的存在直接影响变压器导致其保护回路中二次谐波制动误闭锁方面的研究还有待进一步深入。
本文通过研究HVDC引发直流偏磁的机理及直流偏磁对变压器励磁电流和工作状态的影响,分析了直流偏磁的存在导致变压器差动保护回路中二次谐波制动误闭锁的可能性。通过对有、无直流偏磁下变压器差动电流的电气特征和谐波特性进行仿真分析,提出了判别直流偏磁的新判据,并通过改进现有二次谐波制动保护算法消除了直流偏磁对差动保护可能带来的影响。
1 高压直流输电引发直流偏磁的机理及其对变压器的影响分析
1.1 高压直流输电引发直流偏磁的原理
超、特高压直流输电系统在单极闭锁或检修等特殊工况下会运行于单极-大地模式,引发直流接地极附近的交流变压器产生直流偏磁,其原理如图1所示。
通过将换流站等效为直流电源和内阻,其余各部分分别等效为直流电阻,可以将图1进行简化,简化后等效电路如图2所示。

图1 高压直流输电引发直流偏磁原理Fig.1 Schematic of DC bias caused by HVDC transmission
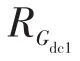
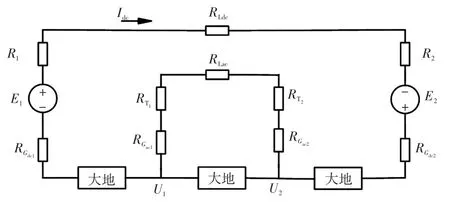
图2 高压直流输电引发直流偏磁的简化原理Fig.2 Simplified schematic of DC bias caused by HVDC transmission
由图2可知,直流偏磁可表示为

交流变压器接地点与直流接地极之间的距离决定了其接地点地电位U1和U2,由式(1)可知,当U1和U2确定时,直流偏磁与变压器的直流电阻、交流输电线路的等效直流电阻和变电站的接地电阻有关。
1.2 直流偏磁对励磁电流的影响
变压器的直流偏磁会引起变压器振动加剧,铁芯以及绕组局部过热、温升增加以及损耗增大。严重情况下产生的大量二次谐波会导致继电保护误动作,尤其对变压器差动保护二次谐波制动的影响更加严重。详细分析如下。
变压器原理如图3所示。N1和N2分别是变压器的一次侧和二次侧匝数,Φ是变压器铁芯磁通,u1和u2分别是变压器一次侧和二次侧电压,其有效值分别为U1和U2,i1和i2分别是变压器一次侧和二次侧电流。

图3 变压器直流偏磁原理Fig.3 Schematic of DC bias in transformer
当变压器发生直流偏磁时,假设直流电流为iDC,从变压器一次侧流入,那么此时变压器一次侧电流为

一次侧电压由于系统支撑,可认为基本为工频正弦量,表示为
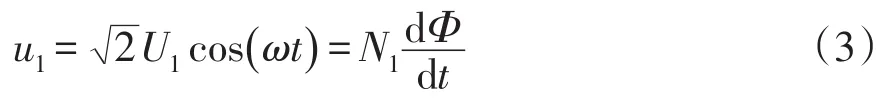
根据磁动势平衡可以得出

式中:H为磁场强度;l为磁路长度。
根据变压器的磁化曲线的几何形状,一般用双曲函数进行拟合,表示为

式中:B为磁感应强度,B=KΦ/A,K为漏磁系数,A为铁芯横截面积;x、y为常数,与变压器铁芯磁化取向有关,通常大于1。
将式(5)代入式(4),可以得到
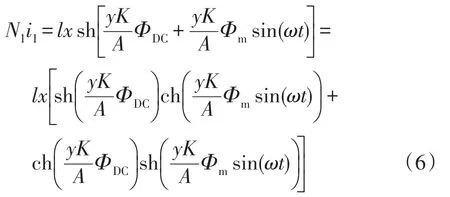
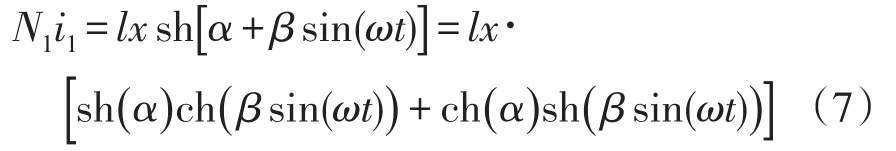
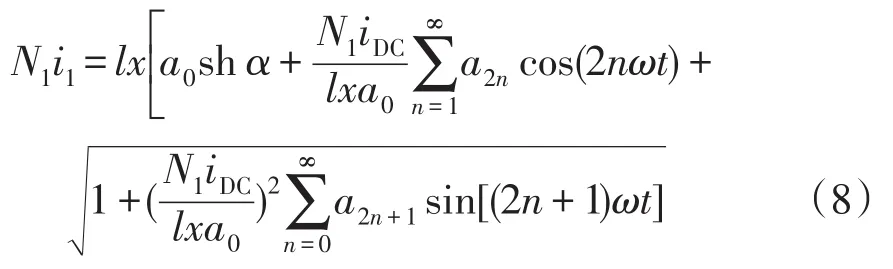
其中,a0、a1、a2是与β相关的系数,分别表示为
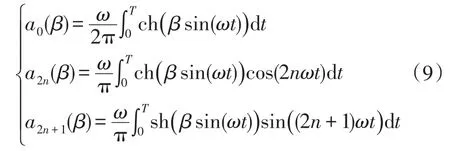
由式(8)可以看出,在直流偏磁的影响下一次侧电流i1中除了基波之外,还含有大量的高次谐波。
变压器二次侧差动回路中的电流为

由于变压器对于高次谐波不具有良好的传变特性,因此变压器二次侧电流中高次谐波含量与一次侧有较大差异,当一次侧有直流电流入侵时,根据式(8)和式(10)可知差动电流中将会出现大量的谐波。其中二次谐波的出现在理论上有导致二次谐波制动误闭锁的可能性。
2 直流偏磁对变压器差动保护二次谐波制动的动作特性的影响
2.1 理论分析
当电力变压器空载投入或外部故障切除后电压恢复时会产生很大的励磁电流,其值可达到额定电流的6~8倍,这个电流就是励磁涌流。变压器差动保护需要躲过励磁涌流,使其在励磁涌流发生时不会发生误动作。
励磁涌流识别方法主要包括:二次谐波原理、间断角原理、波形对称原理、磁通特性原理等[10],工程上多采用二次谐波原理。它以励磁涌流中含有大量的低次谐波分量,尤其是二次谐波的特性为依据,根据电力系统故障时二次谐波含量很少,而励磁涌流中含有大量二次谐波的特点,通过检测差动保护回路的差流中二次谐波的占比来判别励磁涌流[11]。二次谐波制动原理的判断依据有最大相制动、分相制动、综合制动和3取2制动共4种制动方式,一般采用最大相制动方式,其二次谐波制动系数[12]为

式中:IdA1、IdB1、IdC1分别是A、B、C三相差动回路中基波电流的有效值;IdA2、IdB2、IdC2分别是A、B、C三相差动回路中二次谐波电流的有效值。K2的整定值一般取0.15~0.20。励磁涌流持续时间一般为0.5 s左右。由上可知,最大相制动方式能够很好地识别励磁涌流并对保护进行闭锁。但是当合闸于带有故障的变压器时,因非故障相二次谐波的制动作用使得差动保护有延迟,当励磁涌流过后才会动作。
以第1节中对直流偏磁下励磁电流的理论分析为基础,结合式(11)可知直流偏磁带来的大量二次谐波在理论上有造成二次谐波制动误动作的可能性。其将直流偏磁误判为励磁涌流对差动保护长时间进行闭锁,导致发生区内故障时差动保护延迟动作甚至拒动。
2.2 仿真分析
本文以张北柔直工程中换流变压器的实际参数为依据,选择额定容量为850 MV·A的大型变压器为研究对象,其参数如表1所示。
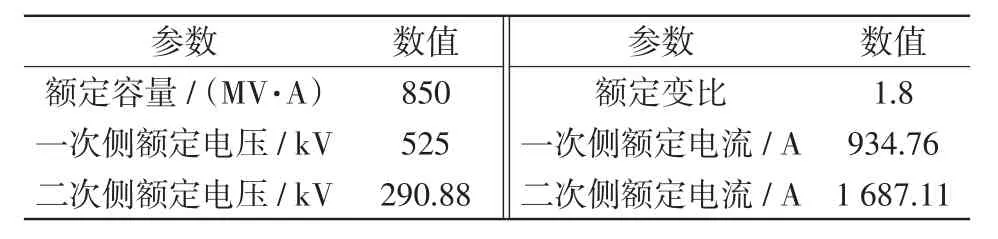
表1 变压器参数Tab.1 Transformer parameters
在PSCAD仿真软件中搭建该变压器模型,通过仿真得到不同直流偏磁下变压器二次回路差动电流中基波与二次谐波的有效值及二次谐波有效值的占比如表2所示。
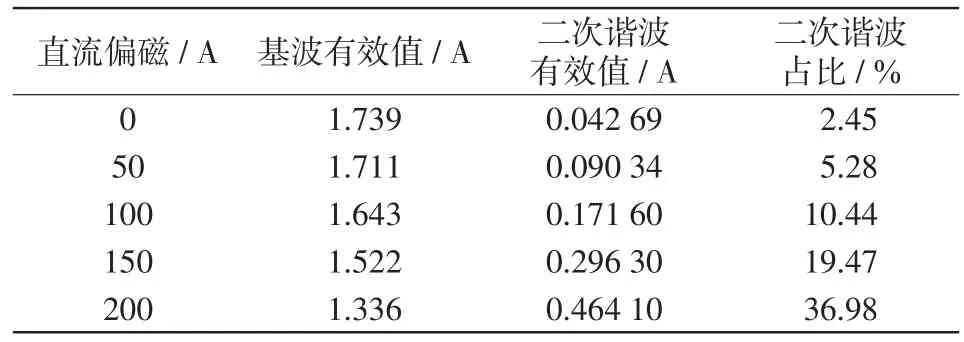
表2 不同直流偏磁下差动电流中基波与二次谐波的有效值Tab.2 Effective values of fundamental wave and second-order harmonic in differential current under different DC biases
由于二次谐波制动系数为15%~20%,根据表2可知当直流偏磁值为200 A时二次谐波占比大于20%,此时会对二次谐波制动的正确动作产生影响,因此考虑对200 A及以上的直流偏磁情况进行具体分析。
首先针对在励磁涌流期间直流偏磁对二次谐波制动的影响进行分析。通过仿真得到无直流偏磁和200 A直流偏磁的情况下变压器励磁涌流期间二次回路中的三相差动电流,如图4所示。
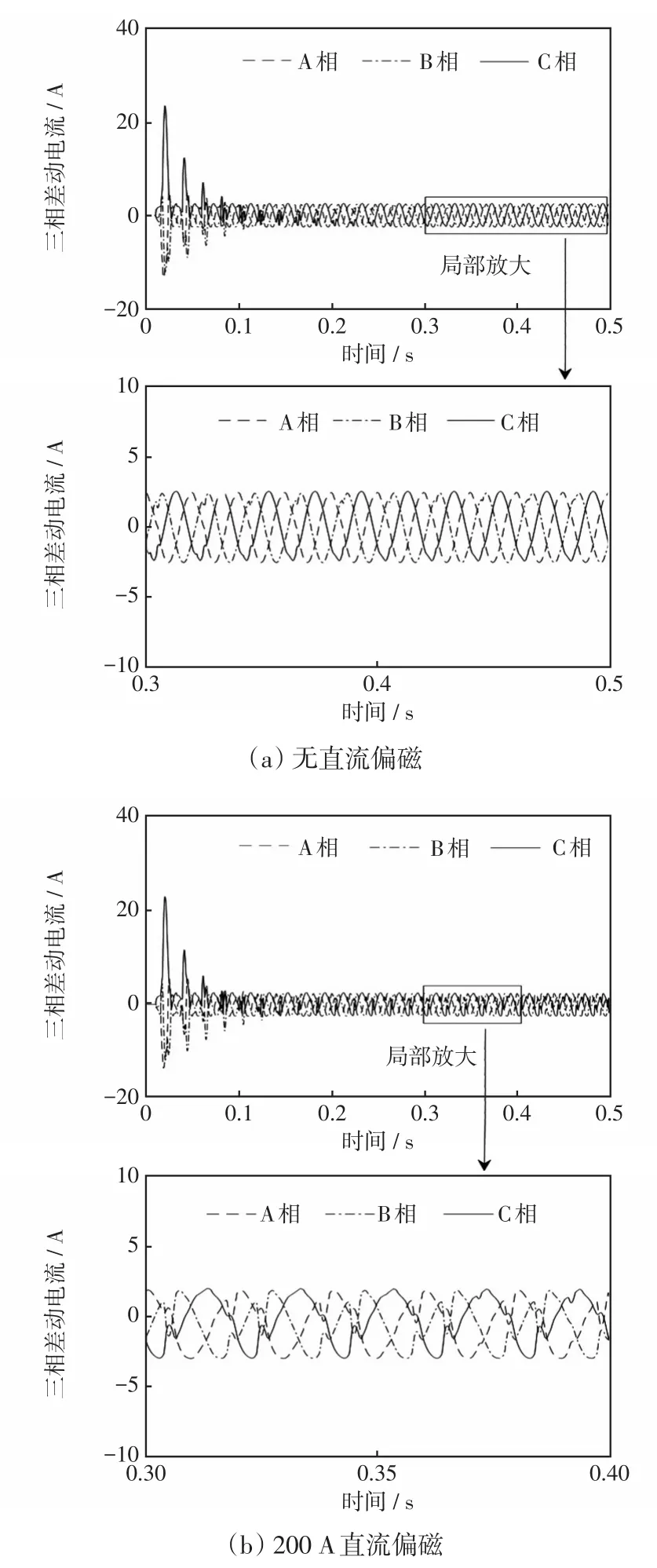
图4 不同直流偏磁情况下二次回路中的三相差动电流Fig.4 Three-phase differential current in secondary circuit under different DC biases
由图4可以看出,励磁涌流期间无直流偏磁时差动电流最大值为23.427 A,200 A直流偏磁时差动电流最大值为22.638 A,都远远超出了差动电流的整定值,不影响二次谐波制动判据。由此可以得到,励磁涌流期间直流偏磁对二次谐波制动判据产生的影响可以忽略不计。
针对不同直流偏磁情况下的差动电流进行谐波分析。变压器外部故障切除后电压恢复时,通过仿真可以得到在没有直流偏磁的情况下,二次回路差动电流的波形如图4(a)所示。此时差动电流的谐波特性如图5所示。
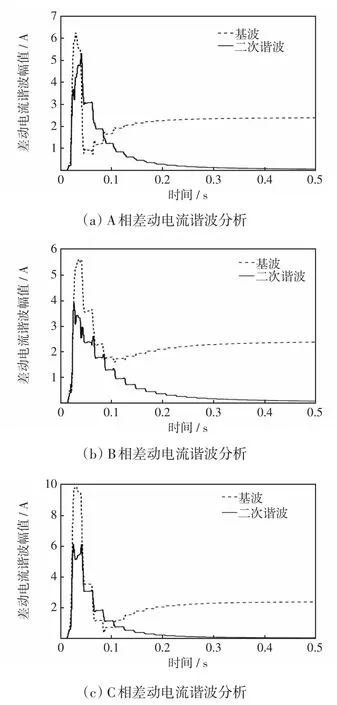
图5 无直流偏磁无故障运行时的差动电流谐波分析Fig.5 Harmonic analysis of differential current without DC bias or fault
从图4(a)可以看出,在励磁涌流过后差动回路中有稳定的不平衡电流,其最大值约为2.3 A,此电流不会引起差动保护动作。从图5可以看出,励磁涌流期间,每一相差动电流中都含有大量谐波。励磁涌流过后谐波逐渐衰减直至消失,差动电流中只含有基波。
针对200 A直流偏磁的情况进行分析。通过仿真可以得到在200 A的直流偏磁下二次回路中差动电流的波形如图4(b)所示,其谐波特性如图6所示。从图4(b)可以看出,在励磁涌流过后,差动回路中有含高次谐波的周期性不平衡电流,此电流也不会引起差动保护动作。
从图6可以看出,直流偏磁存在时,励磁涌流期间每一相的差动电流中同样含有大量谐波。励磁涌流过后偶次谐波逐渐衰减至不为零的常数并保持稳定,此时差动电流中仍含有大量的二次谐波。这个由直流偏磁引发的二次谐波可能会引起二次谐波制动将差动保护闭锁,此时若发生区内故障则保护无法正确动作。
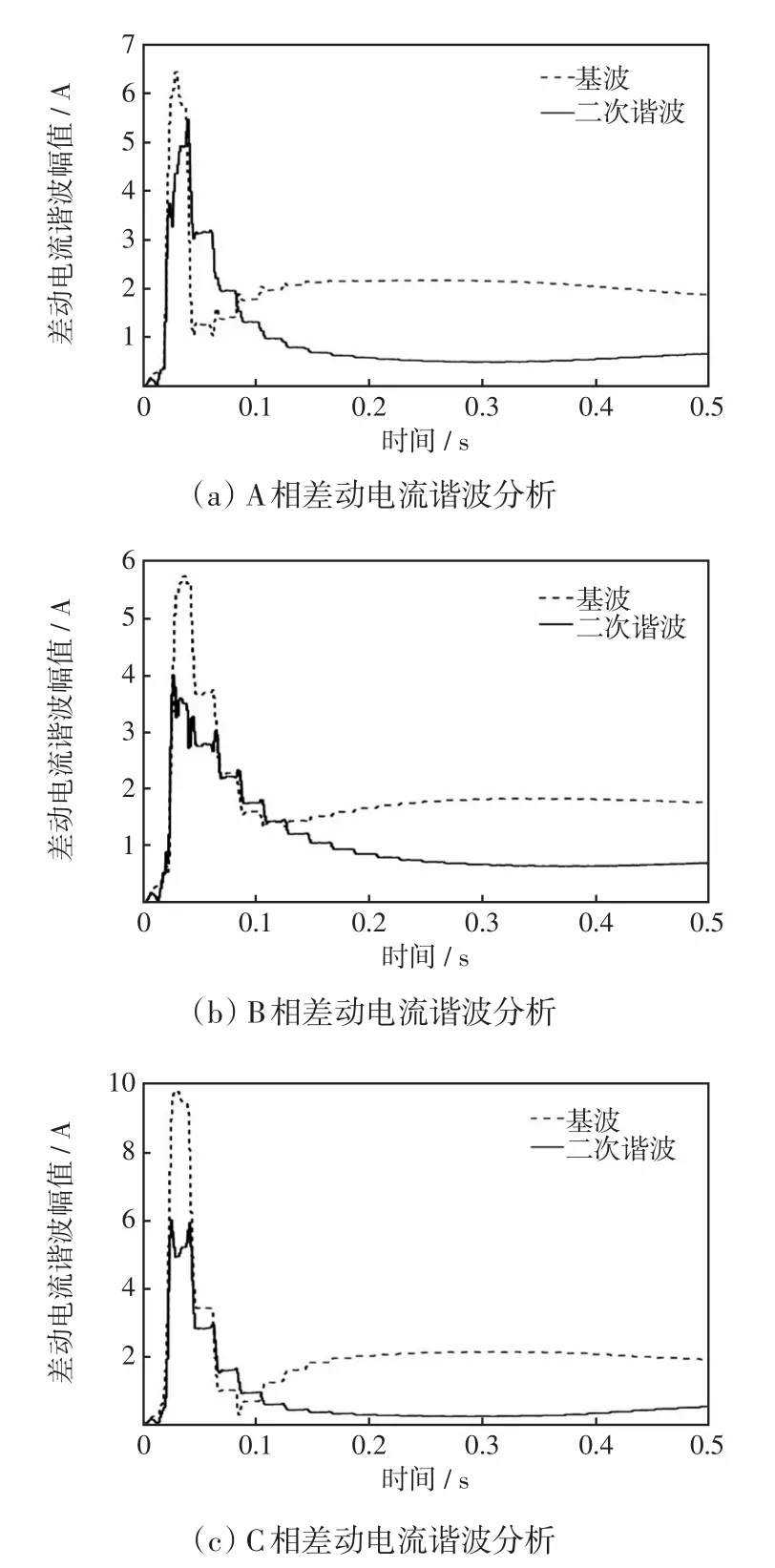
图6 200 A直流偏磁下无故障时的差动电流谐波分析Fig.6 Harmonic analysis of differential current without fault but under 200 A DC bias
对200 A直流偏磁下发生区内相间故障的情况进行仿真分析。当发生区内BC相间短路故障时,二次回路中差动电流波形如图7所示。此时二次回路中差动电流的谐波特性如图8所示。

图7 200 A直流偏磁下BC相间短路时的差动电流Fig.7 Differential current under short-circuit between phases B and C and 200 A DC bias
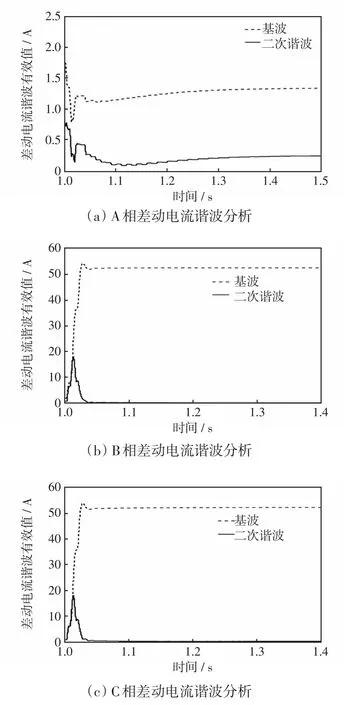
图8 200 A直流偏磁下BC相间短路时差动电流谐波分析Fig.8 Harmonic analysis of differential current under short-circuit between phases B and C and 200 A DC bias
由图7可以看出,当发生区内BC相间短路故障后,A相差动电流最大值减小至2.2 A左右并出现尖峰。B、C相差动电流瞬间增大至72 A左右并且波形没有明显畸变,这是因为BC相间短路后一次侧电流不流入变压器。
由图8可以看出,B、C两相的差动电流在故障发生瞬间都有高次谐波产生并在一个周期左右衰减至0,基波瞬间增大至52 A左右,极大地拉开了基波与二次谐波之间的差距。而A相在故障前由于直流偏磁的存在导致差动电流中二次谐波含量较高,且故障瞬间产生的高次谐波不会衰减至0,而是与基波呈现相同的变化趋势并稳定在一个定值,此定值为基波的15%~20%。
图8的结果表明,二次谐波制动可能会引起差动保护闭锁导致保护拒动。
3 基于直流偏磁和励磁涌流判别的二次谐波制动改进算法
3.1 直流偏磁与励磁涌流的判别方法
根据第2节中的分析可知,变压器差动保护的二次谐波制动原理是利用了励磁涌流中含有大量二次谐波的特性来闭锁差动保护以防止励磁涌流引起的误动。此外,变压器发生直流偏磁时也会引起二次谐波的出现。此时发生区内故障时某一相差动电流中二次谐波与基波的比值可能会达到0.15及以上,二次谐波制动算法会将直流偏磁下的故障电流误判为励磁涌流而将差动保护闭锁,引起保护的拒动。因此,在二次谐波制动闭锁之前需要判别二次谐波的来源是励磁涌流还是直流偏磁。
首先对励磁涌流非周期分量的衰减规律进行分析。不同情况下变压器二次回路的差动电流中基波和各次谐波的变化规律,如图9所示。
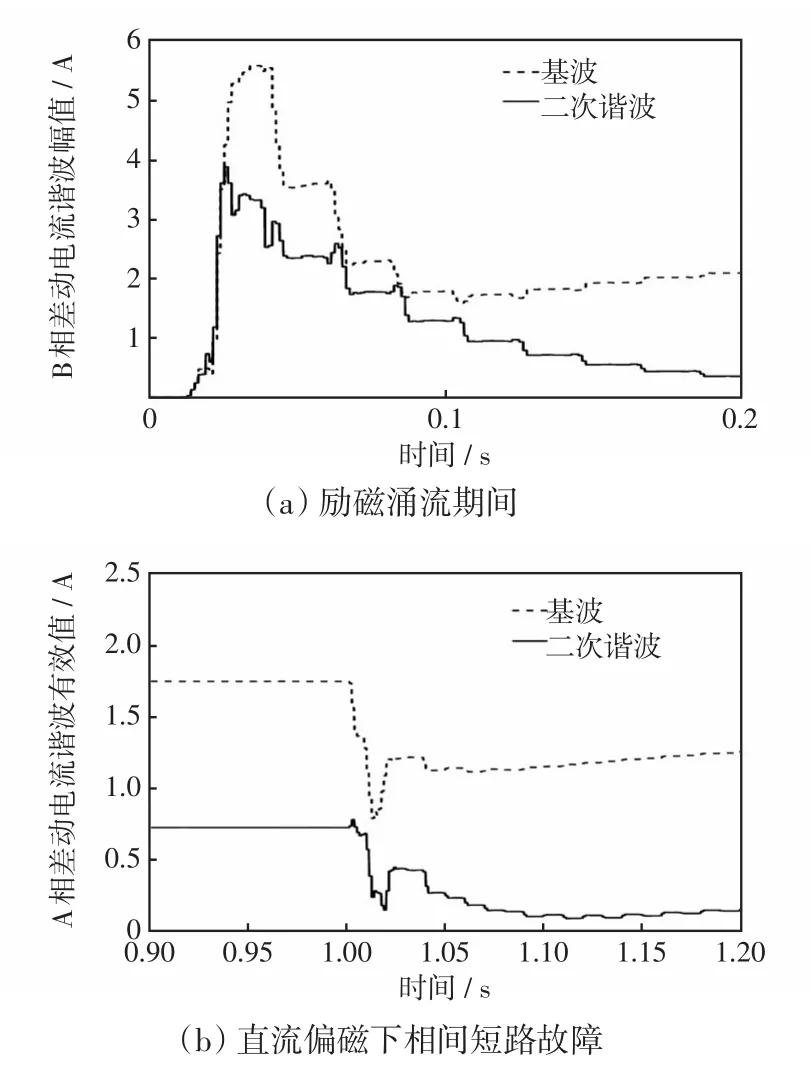
图9 不同情况下差动电流的谐波分析Fig.9 Harmonic analysis of differential current in different cases
从图9(a)可以看出,变压器励磁涌流期间,差动电流中的基波和二次谐波在第1个周期内迅速上升并接近顶峰。此后二次谐波开始呈“阶梯”状衰减,即每个周期内的值基本不变,每过一个周期都会有一次大幅下降。励磁涌流发生后第1~4个周期中二次谐波的平均有效值见表3。

表3 励磁涌流发生后1~4个周期内差动电流中基波和二次谐波的平均有效值Tab.3 Average effective values of fundamental wave and second-order harmonic in differential current during 1—4 periods after inrush current
从图9(b)可以看出,在200 A直流偏磁的情况下,当发生相间短路故障时,非故障相差动电流的基波分量会瞬间下降并在故障后的一个周期内趋于稳定。二次谐波在第2周期内小幅度下降后趋于稳定,这与励磁涌流期间的二次谐波的“阶梯”变化有较大不同。故障发生后第1~4个周期中二次谐波的平均有效值见表4。
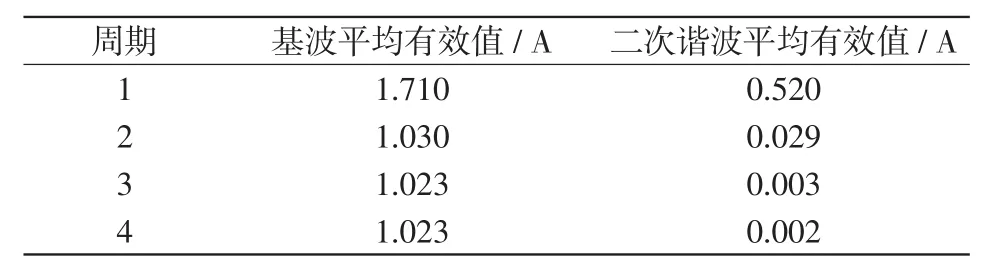
表4 区内故障发生后第1~4个周期内差动电流中基波和二次谐波的平均有效值Tab.4 Average effective values of fundamental wave and second-order harmonic in differential current during 1—4 periods after area fault occurrence
由表3和表4可以看出,在励磁涌流发生后的4个周期内,相邻周期之间差动电流中的二次谐波平均有效值分别下降了0.51 A、0.50 A和0.52 A,大体呈现出等差递减的“阶梯”下降规律。直流偏磁存在时区内故障发生后相邻周期之间差动电流中的二次谐波平均有效值分别下降了0.491 0 A、0.025 8 A和0.001 0 A,二次谐波在故障瞬间有较大波动,但之后3个周期内基本不变。因此可以通过比较故障电流突变后的第2和第3周期内二次谐波平均有效值差的绝对值来判别二次谐波是由励磁涌流引起的还是直流偏磁引起的,从而决定保护是否闭锁。
励磁涌流和直流偏磁的判别原理为

3.2 二次谐波制动保护算法改进
变压器差动保护二次谐波制动改进后的算法如图10所示。
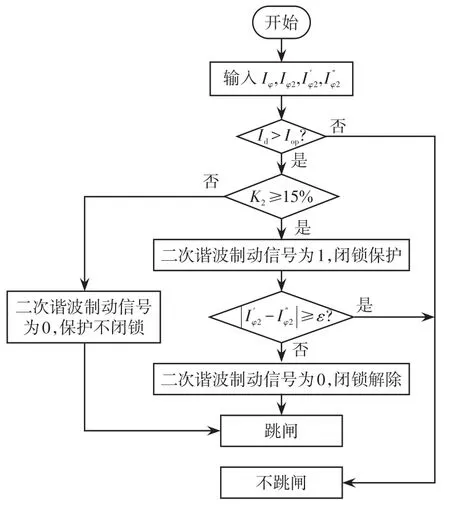
图10 二次谐波制动保护改进算法Fig.10 Improved algorithm of second-order harmonic braking protection
根据传统变压器差动保护的二次谐波制动原理,先在原有算法基础上添加新的门槛来判别二次谐波是由励磁涌流还是直流偏磁引起的,然后再决定是否闭锁差动保护,以避免直流偏磁期间发生故障时差动保护拒动。
图10中的逻辑过程如下。
(1)判断差动电流是否达到整定值。若达到整定值,说明可能发生了励磁涌流或者区内故障。
(2)判断二次谐波制动系数是否超过整定值15%,若超过了说明可能是励磁涌流引起的,保护闭锁。闭锁持续3个周期。
这样能够使得差动保护在直流偏磁影响下正确响应区内故障。在这种方法中,若是由于励磁涌流引起二次谐波含量增大的情况,与传统保护一样不会引起误动。若是发生区内故障时由于直流偏磁的存在引起二次谐波含量增大,则相对于没有直流偏磁时会延迟2个周期动作时间跳闸,但是比传统算法下发生拒动的情况要好很多。
3.3 仿真验证
在PSCAD中搭建变压器模型,其参数如表1所示。在0 s时给变压器供电,合闸瞬间会出现励磁涌流。设定在1.0 s时发生区内BC相间短路故障,故障持续时间为0.5 s。在没有直流偏磁的情况下,基于二次谐波制动的差动保护的跳闸信号如图11所示。
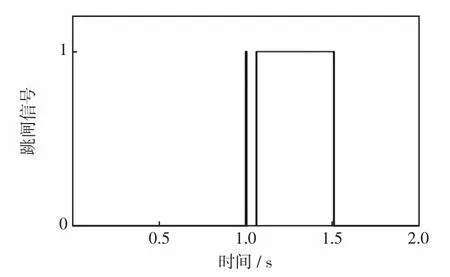
图11 无直流偏磁时差动保护的跳闸信号Fig.11 Trip signal of differential protection without DC bias
从图11可以看出,在没有直流偏磁的情况下,基于二次谐波制动的差动保护在变压器启动瞬间的跳闸信号保持为0,能够较好地防止励磁涌流引起差动保护误动作。但是当在1.0 s时发生故障后,跳闸信号延迟动作了3个周期,这是由于故障瞬间引起的高次谐波波动导致二次谐波制动对保护闭锁引起的延迟。由于故障产生的二次谐波很小且衰减很快,所以在微小的延迟后保护能够正确动作。
当分别在200 A和300 A的直流偏磁下发生区内故障时,基于二次谐波制动的差动保护的跳闸信号如图12所示。
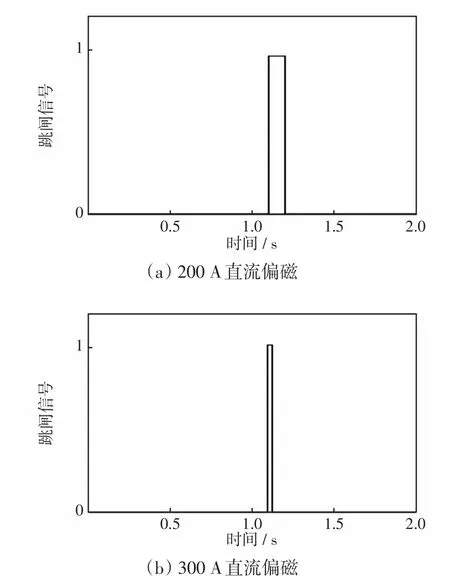
图12 不同直流偏磁值时差动保护的跳闸信号Fig.12 Trip signal of differential protection under different DC biases
根据图12可以看出,若变压器运行于200 A直流偏磁下,此时在故障发生3个周期之后跳闸信号变为1,且持续时间只有0.1 s。若变压器运行于300 A直流偏磁下,在故障发生3个周期之后跳闸信号变为1,但持续时间仅有0.03 s,断路器无法正常开断,故障无法切除,保护拒动。
对于基于改进后的二次谐波制动的差动保护而言,当在300 A的直流偏磁下发生区内故障时,跳闸信号如图13所示。
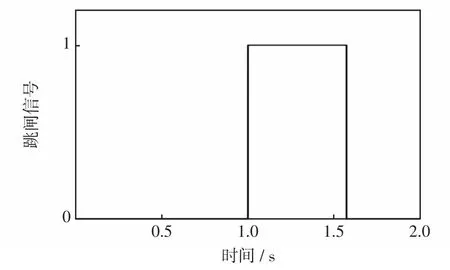
图13 300 A直流偏磁下改进后的差动保护的跳闸信号Fig.13 Trip signal of improved differential protection under 300 A DC bias
由图13可以看出,改进后的基于二次谐波制动的差动保护在发生区内故障时跳闸信号能够持续正确反映故障情况来使得断路器跳开。这样在避免励磁涌流引起保护误动的同时,消除了变压器在有直流偏磁的情况下发生区内故障时差动保护拒动的可能性。
4 结论
(1)研究了由高压直流输电引发直流偏磁的机理,分析了入地电流的流通路径,理论分析了直流偏磁对变压器工作状态和对励磁电流的影响。
(2)研究了传统变压器差动保护二次谐波制动原理以及变压器励磁涌流的特性,从理论上分析了直流偏磁对二次谐波制动判据的影响,得到了直流偏磁可能会引起二次谐波制动误闭锁差动保护的结论。
(3)分别针对有直流偏磁和没有直流偏磁存在的情况,对无故障正常运行和发生区内相间短路故障时的差动电流进行仿真分析,验证了直流偏磁引起二次谐波制动误闭锁的可能性。通过对比分析励磁涌流和直流偏磁下差动电流的谐波特性,提出了新的直流偏磁判据原理,改进了传统二次谐波制动保护判据,从而消除了直流偏磁引起二次谐波制动误闭锁的可能性。仿真验证了改进后算法的有效性。

