大型核电汽轮发电机非全相运行转子动态电磁力分析

戈宝军， 姜超， 吕品， 陶大军， 林鹏， 殷继伟， 赵洪森

(哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080)

0 引 言

在非全相工况下，大型核电汽轮发电机的转子不仅受到极大的电磁力及电磁转矩，而且外部电网会受到巨大的不良影响。因汽轮发电机转子长期运行过程中受到结构动态应力、磁应力、热应力等许多种因素共同作用而易造成局部机械疲劳。如果非全相运行时电磁力的集中位置正好在机械疲劳处，极有可能导致转子的绕组、绝缘以及转子硅钢片等部件的损坏。同时，对非全相运行时电机转子各部分电磁力分布的研究为电机设计及制造提供参数，以保障电机各组件机械强度裕量，从而保障电机在非全相运行时转子不受损害。

电力系统的缺相运行称为非全相运行。非全相运行是电力系统中发电机常见的非正常运行的状态，同时，也是电力系统所有故障中最为严重的故障之一。具体原因为开关没有全相的分与合，线路出现非对称的故障，电力系统负荷出现不对称等。此时如果不及时采取有效措施，极易导致重大机组设备事故与电网事故，严重地影响到发电机组与电网运行的安全[1-3]。如果电机振动过大，不但会引起转子动静摩擦，而且可能引起汽轮机转子叶片严重损坏，以及各轴瓦的损坏，甚至烧毁。对于采用氢气内冷却的汽轮发电机组，若振动过大损坏密封瓦，造成漏氢，则极有可能引起氢气爆炸，从而扩大事故[4-5]。因此，计算非全相运行电机转子电磁力，并研究转子各部分电磁力的动态变化规律，具有十分重要的理论价值。

国内外学者对电机电磁力计算进行了大量的研究工作，提出了许多研究方法。文献[6]运用麦克斯韦应力法，结合场-路耦合仿真模型详细研究了大型汽轮发电机空载三相突然短路时转子各部分动态电磁力的分布及规律；文献[7]分析了汽轮发电机转子绕组匝间短路工况不平衡磁拉力问题，比较了解析法与数值法计算磁拉力的精确性，而且得到了不平衡磁拉力和发电机运行状态间的关系。文献[8]运用洛仑兹力原理与麦克斯韦应力法，对电机故障前后的导条、转子铁心所受到的电磁力进行计算，与实际测得的电机转矩值相对比，验证了该方法准确性。文献[9]对感应电动机单相短路故障时的定、转子齿部不同位置局部电磁力进行了计算，并给出了转子所受电磁力波分布规律。文献[10] 针对汽轮发电机内部局部的电磁力，采用虚位移方法来计算，从而得到每个部分的电磁力的变化情况。文献[11]针对直线电机，从理论推导的层面分析电机内部的电磁力分布情况。文献[12]针对汽轮发电机转子发生裂纹现象，分析了在额定工况下转子的铁心表面的电磁力波变化情况；文献[13]首先分别分析了转子静、动偏心及转子绕组匝间短路各单一故障时转子不平衡电磁力分布情况，然后，通过矢量叠加得到复合故障时转子所受不平衡电磁力的解析表达式。文献[14]研究并深入分析了偏心故障时的电机内部三维电磁力分布，得到了转子径向力在不同的偏心程度时分布结果。文献[15]将2种极化模型的电磁力计算法进行了全面的理论推导及应用研究。文献[16]针对汽轮发电机局部电磁力密度，结合虚位移法研究推导了新的算法。文献[17]针对无轴永磁电机，建立数学模型，提出了转子磁悬浮的电磁力解析公式。

众多国内外学者对电机转子电磁力分布进行了大量研究，但综合他们的研究成果可知：在研究过程中，很少把电网考虑进去，且发电机多是单机负载下运行。此情况下，对发电机各种工况下各部分电磁力分布情况的研究，并不能准确全面的反映电机实际的工作情况。因此，对发电机非全相工况下转子动态电磁力分布情况的研究很有参考价值。

本文建立了场-路-网耦合的时步有限元模型，该模型适用于发电机并网运行，运用麦克斯韦应力法详细分析了发电机非全相运行情况下电机转子电磁力分布及其规律。由于汽轮发电机非全相运行情况较多，包含的工况十分复杂，Yd连接方式的升压变压器高压侧断开工况下，发电机的非对称运行，就是本文中的非全相运行工况，其中升压变压器只有一相断开。与此同时，分析计算了发电机并网额定运行工况下转子动态电磁力分布及其规律，并把计算结果和发电机非全相运行工况下的结果做对比，为大型汽轮发电机的故障诊断与优化设计等提供理参考。

1 场-路-网模型与电磁力计算方法

1.1 发电机时步有限元模型

以汽轮发电机为例，其容量为1 407 MV·A，该汽轮发电机的参数如表1所示。

表1 大型汽轮发电机的参数

为了简化计算，做以下合理假设：

1)假设电机内部为似稳电磁场，不计位移电流大小，忽略电磁场频率变化；

2)假设电机内磁场具有周期性及电机实际结构的完全对称性，取其一对磁极的一半作为求解区域，如图1中所表示；

3)假设仅顾及定转子轴向电流(z方向分量) ，将电机有效长度内的磁场视为二维平行平面场；

4)假设忽略定转子绕组中的集肤效应和电网中的高次谐波作用对电机内部磁场的影响；

5)假设铁心材料有单值磁化曲线，忽略铁磁材料的磁滞效应和定转子铁心的叠片结构对磁场的影响。

根据以上的假设条件，建立汽轮发电机的二维有限元计算模型，如图1所示。

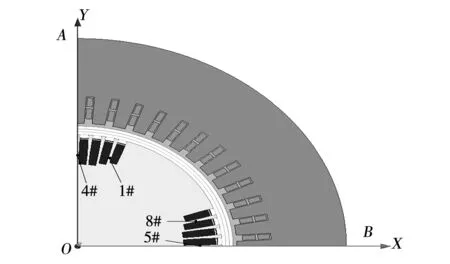
图1 大型汽轮发电机的有限元计算模型Fig.1 Finite element calculation model of large steam turbine generator

当利用时步有限元法计算发电机内的电磁场分布时，考虑其相应边界条件，非线性二维平面场用磁矢量AZ位描述时，瞬变电磁场定解问题可以表达为：

(1)

式中：电机矢量磁位的z轴分量为AZ；σ为电机材料的电导率；μ为电机材料的磁导率；JZ为源电流密度。

1.2 建立场-路-网耦合模型

针对大型发电机单机无穷大系统，它的等值电路主要包含汽轮发电机、转速控制系统、励磁调节系统、升压变压器、双回输电线路以及无穷大系统。

为了准确模拟并网运行大型核电汽轮发电机发生非全相运行工况，构建了发电机场-路-网耦合时步有限元模型，其中发电机容量为1 407 MV·A，汽轮发电机系统通过150 km的双回架空输电线与无穷大电网系统连接，升压变压器连接组标号为YNd11。本文所指的非全相运行是指升压变压器高压侧断路器一相断开情况下，发电机的不对称运行状态。

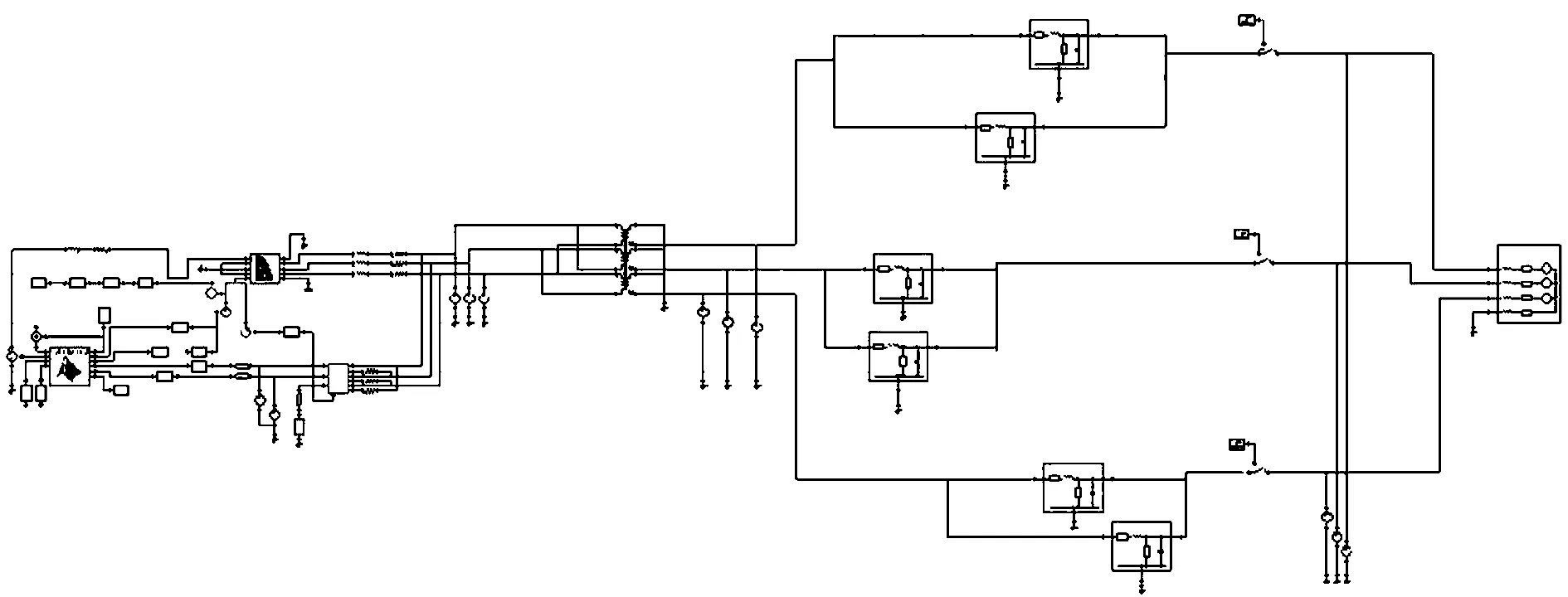
图2 汽轮发电机非全相运行场-路-网耦合仿真系统结构框图Fig.2 Structure diagram of field-circuit-network coupled simulation system for turbo generator under open-phase operation condition

发电机非全相运行时，定子绕组三相电流出现不对称的情况，采用对称分量法，将其分解为正序、负序、零序3个对称分量，其中负序电流产生相对于转子旋转方向反向的旋转磁场。这一旋转磁场在转子本体、槽楔和护环感应出2倍频率的频率电流，该电流在这些部件上和各部件产生较大的磁应力，并且各部分磁应力分布不均，易出现局部机械疲劳，进而损坏电机。当发生故障 (单相故障)时，发电机断路器会在几个周期内快速动作切除故障，以有效地避免对发电机组的损害。因此，分析故障后首周期的转子各部分受力情况具有十分重要的理论意义。

1.3 电磁力模型

为了尽可能精确计算转子横截面上各处磁应力，首先需要获得转子各部分的磁场强度。同时，为了求解，而且也能全面考虑转速改变和励磁变化对电机内磁场的影响，本文采用场-路-网耦合模型进行计算，其中有限元计算部分采用1/4电机仿真模型。

在预处理程序编写时，从定转子2个坐标系分割定转子气隙。为了满足高麦克斯韦应力法对高精度气隙磁场和气隙分割均匀的要求，对气隙层的剖分单元个数增多。同时，在对磁密变化较大转子区域采用深度剖分。本文经过大量试算，最后，在如图1所示转子各区域，共计采用了6 448个单元。

在上述磁密计算的基础上，运用麦克斯韦应力法对电磁力进行计算，采用不同介质交界面上磁应力计算模型计算转子铁心表面和齿槽壁上所受到的电磁力，作用于交界面上面积元上磁应力切向与法向分量为：

(2)

由式(2)可知，磁应力仅仅在法向方向对电机转子各部分有影响，并且由铁心指向空气是该应力的方向。

计算转子产生电磁力应力，获得转子气隙的磁密，利用麦克斯韦应力法，可得出作用于转子上的切向电磁力密度与法向电磁力密度为：

(3)

式中：Bδr、Bδt分别为气隙磁场法向分量与切向分量；μ0为空气的磁导率。

由于气隙空气的磁导率与转子铁心磁导率相差非常大，在交界面上两介质磁导率最大能到百倍，在交界面Ht差别巨大,所以为了有效减小Ht的计算误差，提高计算准确性，以向量磁位A作为未知量的时布有限元法中运用加权平均值，加权公式为

(4)

式中：μFe、μ0分别为定子铁心侧和空气侧的2种媒质的磁导率；Ht(Fe)和Ht(0 )分别为两侧磁场强度的切向分量。

为了全面准确反映转子齿部电磁力分布特点, 将转子小齿编号如图1所示，沿转子旋转方向编号为1#～8#。转子齿一侧有浅槽的小齿壁上由齿顶至齿底均匀取11个关键点，两侧都没浅槽的小齿壁上均匀取10个关键点，具体位置如图3所示，此外，图中由齿表面射出的箭头指向电磁力的法向方向。

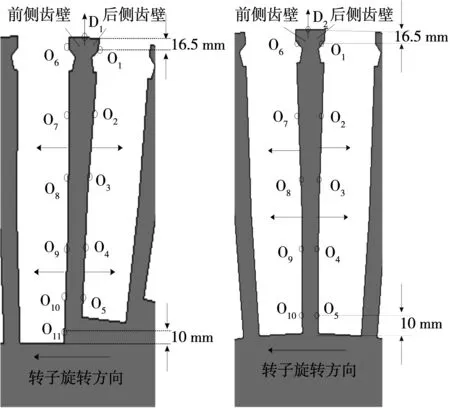
图3 关键点及磁应力的参考方向Fig.3 Key points and referential direction of the magnetic stress

2 非全相运行时动态电磁力计算

2.1 非全相运行动态过程计算

若转子直轴与A相绕组轴线重合，汽轮发电机启动后达到平稳运行时，发生变压器高压侧一相断开故障，即电机非全相运行。由场-路-网耦合模型仿真得断路后5个周期内定子三相电流、电磁转矩变化情况如图4所示。

由图4(a)可知，非全相运行后定子电流随时间的变化畸变越来越严重，首周期中，定子B相电流严重畸变，最大幅值为67 036.1 A,是B相正常工作电流幅值的1.40倍，定子A、C电流同样也发生畸变，电流幅值减小，其幅值为46 178.8 A，是正常工作时的0.93倍。C相的最大值为47 421.9 A，其额定电流最大值的0.97倍。图4(b)电磁转矩的第一个周期内最大值为8 771 456.25 N·m，最小值为3 685 684.50 N·m，分别为额定电磁转矩的1.13倍和0.473倍。由此可知，故障后转子所受电磁冲击非常大。

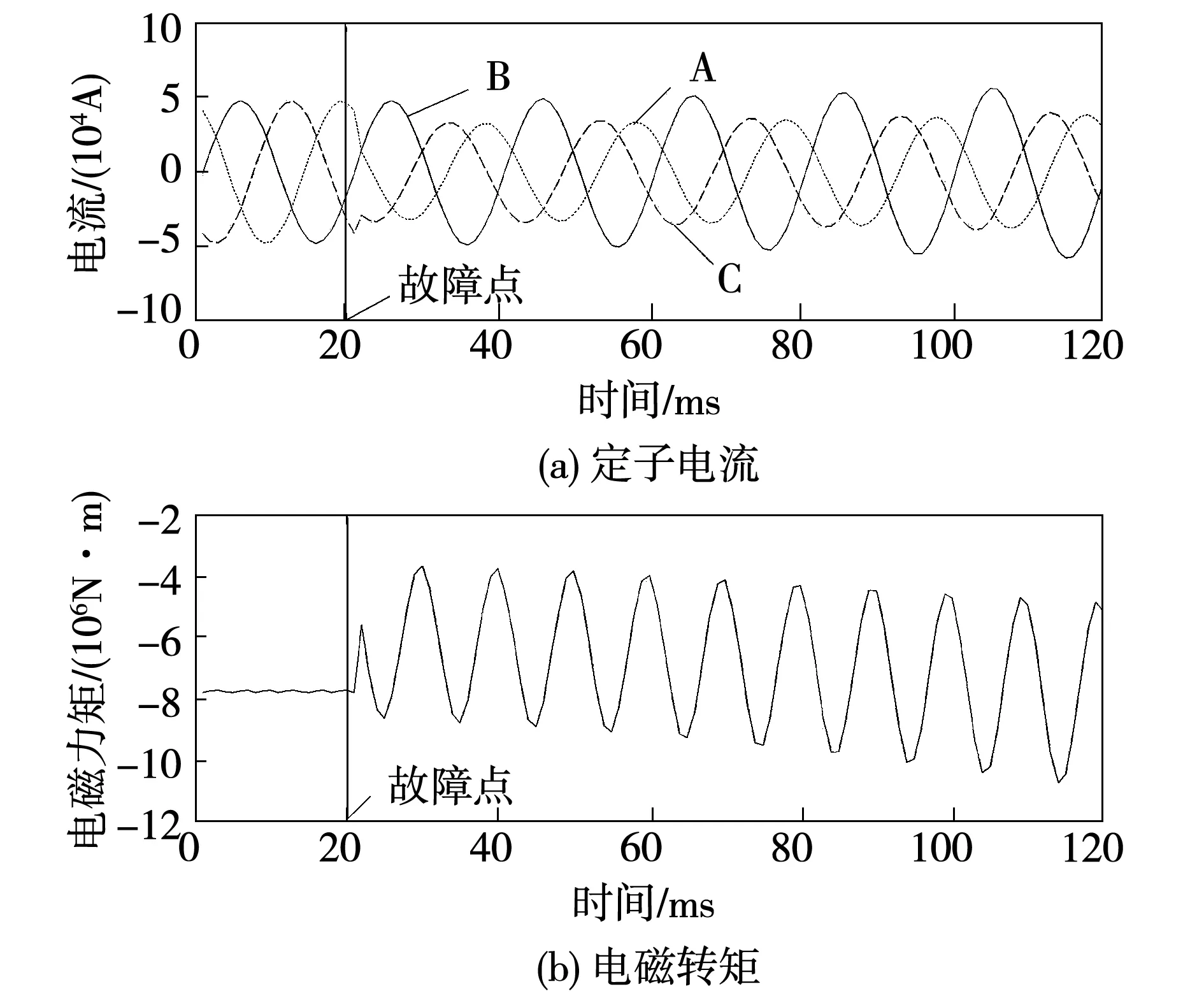
图4 定子电流与电磁转矩Fig.4 Stator current and electromagnetic torque

图5分别为非全相运行后1 /2周期和1个周期以及额定运行时汽轮发电机的磁密云图。

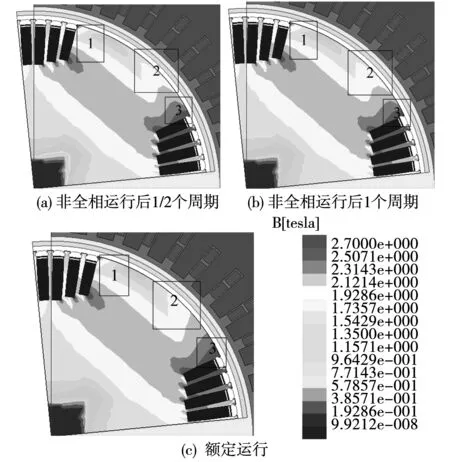
图5 非全相运行工况转子磁密云图Fig.5 Magnetic field density cloud of the rotor in the open-phase operation condition

由图5看出，断路故障后，转子磁场发生畸变，尤其在T/2时刻最为严重。随着电机的运行，磁场分布又逐渐趋于稳定，但分布情况仍保持畸变，明显畸变区域如图中的1、2、3区。在3区，其磁场密度先变大后变小，再变大。而小齿部分磁场强度由齿底向齿顶沿径向逐渐变小。对转子来说，磁场最强的区域位于转子旋转的后边，磁场最弱的区域在旋转方向前边。磁场的分布特点决定了电磁力的分布及规律，为了更准确的反映转子各部分受力的详细情况，对转子齿顶、齿壁受力情况进行详细地分析。

2.2 转子齿顶动态电磁力

由于电机非全相运行后，电机磁场发生畸变，呈现不对称分布，导致转子齿顶的磁应力分布也发生了变化。图6给出了电机故障后沿1/4转子齿顶磁应力的分布。

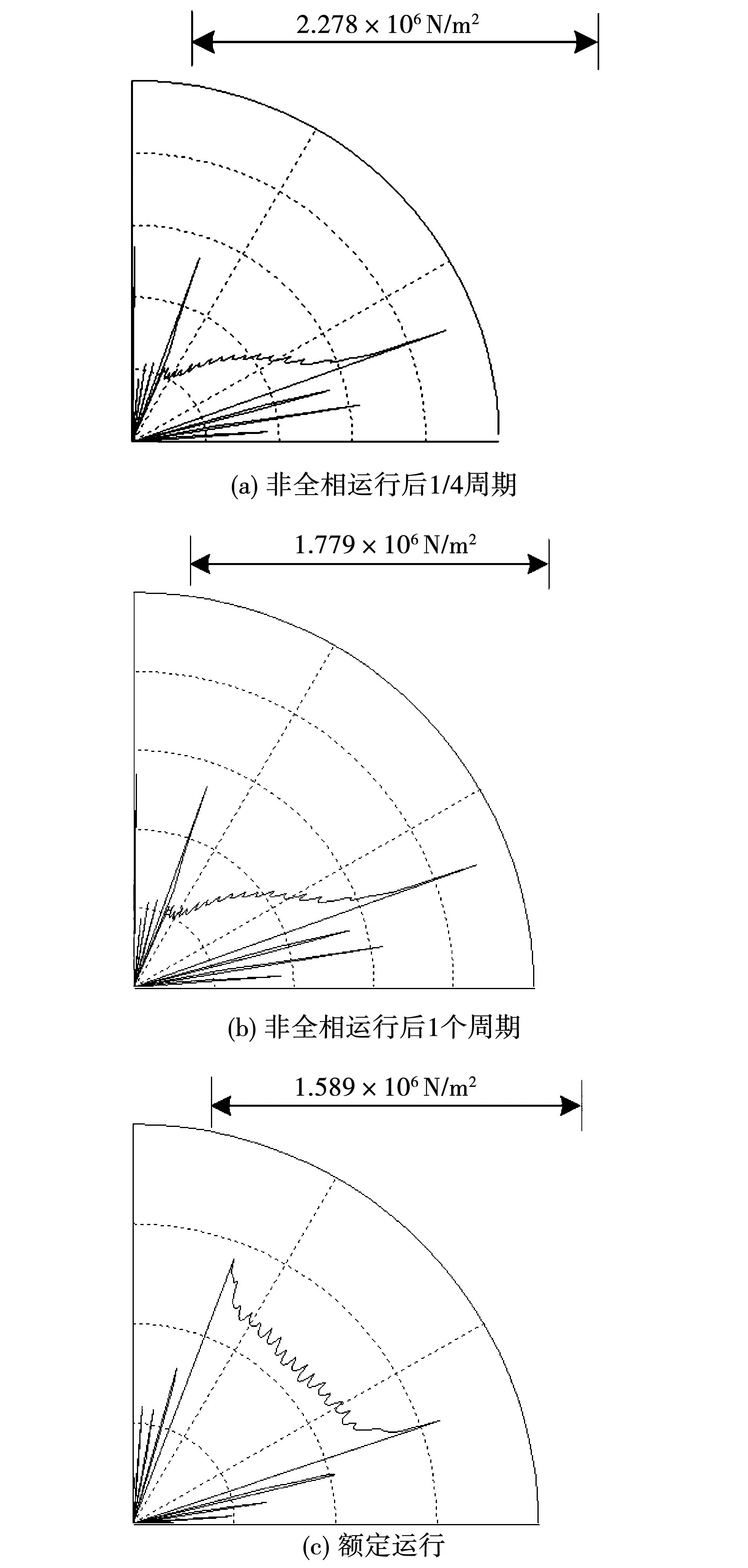
图6 转子齿顶电磁力分布Fig.6 Distribution of electromagnetic stress at the top of the rotor teeth

由图6(a)看出，在变压器高压侧一相断开后的1/4周期，磁应力在汽轮发电机转子齿面上不对称分布。由图6(a)可知，在发电机旋转方向的前方磁应力很弱，而在旋转方向的一侧磁应力后侧则很强。其中，在大齿的齿面上出现磁应力最大值，数值为2.278×106N/m2，为额定运行时相应位置磁应力的1.62倍。小齿部分，最大值出现在7#齿的齿面上，数值为1.57×106N/m2，为额定运行时相应位置磁应力的2.70倍。

由图6(b)看出，在变压器高压侧一相断开后的1个周期，磁应力在汽轮发电机转子齿面上也呈不对称分布。在发电机旋转方向的后侧磁应力很强，而在旋转方向的前方一侧磁应力则很弱。其中，在大齿的齿面上出现磁应力最大值，为1.779×106N/m2，为额定运行时相应位置磁应力的 1.10倍。在小齿部分，最大值出现在7#小齿的齿面，数值为1.513×106N/m2，为额定运行时相应位置磁应力的1.48倍。对比非全相运行后转子齿面首周期的磁应力所有最大值，可知在1/4周期时最大。

由图6(c)看出，当额定运行时，磁应力在汽轮发电机转子齿面上呈现不对称分布，但不对称程度与非全相运行时不对程度相比较小。其中，在发电机旋转方向的后侧受力较大，而在旋转方向的前方一侧受力较弱。其中，在大齿的齿面上出现磁应力最大值，数值为1.598×106N/m2。在小齿部分，最大值出现在8#小齿的齿面，数值为1.023×106N/m2。

电机非全相运行时，由于齿顶位置磁场畸变最为严重，为了更准确反映此情况，图7分别给出了1#齿、3#齿齿顶关键点D1、D2电机稳定运行和非全相运行时一个周期内磁应力的分布。

由图7(a)可知，1#齿顶的关键点D1在故障后一个周期内所受的磁应力最大值为1.508×106N/m2，为额定运行时相应位置相应时刻的1.37倍，其所受磁应力在首周期内波动较为严重。而额定运行时，D1点磁应力在一个周期内的平均值为1.094×106N/m2，其所受磁应力波动不大。由图7(b)可知，3#齿顶的关键点D2在故障后一个周期内所受的磁应力最大值为1.102×106N/m2，为额定运行时相应位置相应时刻的1.40倍。其所受磁应力在首周期内波动十分严重。而额定运行时，D2点磁应力在一个周期内的平均值为0.787×106N/m2，其所受磁应力也波动不大。

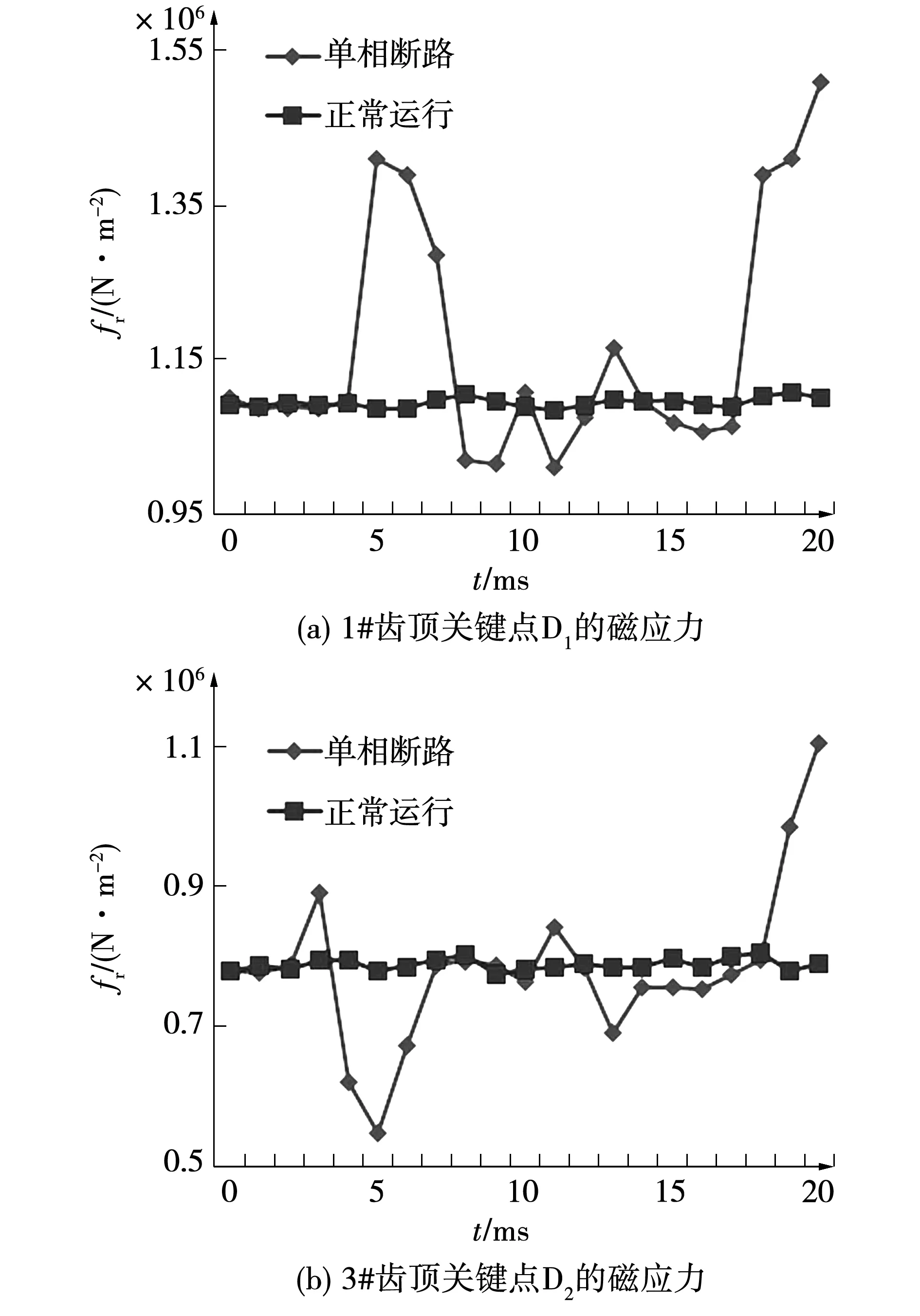
图7 转子齿顶关键点的磁应力Fig.7 Magnetic stress of key points at the top of the rotor teeth

通过对转子1#齿、3#齿齿顶各关键点受力变化情况进行计算可以看出，电机非全相运行工况下，磁场震荡最大的区域在临近气隙区，所以齿的顶端上关键点受力较正常负载运行时波动明显；并且转子小齿一侧有浅槽时小齿齿顶所受磁应力较一侧无浅槽小齿大。由此表明，电机转子槽型的设计对于齿顶受力影响很大。

2.3 转子齿壁动态电磁力

汽轮发电机非全相运行后首周期内1#小齿两侧齿壁上关键点所受应力情况如图8所示。1#小齿的11个关键点编号、位置及电磁力正方向如图3(a)中所示。

由图8可知，当汽轮发电机突然非全相运行后首周期内，在1#齿的两侧齿壁上各关键点所受应力不相等。关键点O1在前侧齿壁所取的点中最靠近转子的齿面，其所受磁应力的最大值为3.120×106N/m2，是所有在该侧齿壁关键点所受最大应力平均值的1.608倍，是与它最近关键点O2的1.581倍。在后侧齿壁所有的关键点中，关键点O6最靠近齿面，其所受磁应力最大值2.947×106N/m2，是所有的在该侧齿壁上关键点所受最大磁应力平均值的1.193倍，是与它最近的关键点O7的1.402倍。

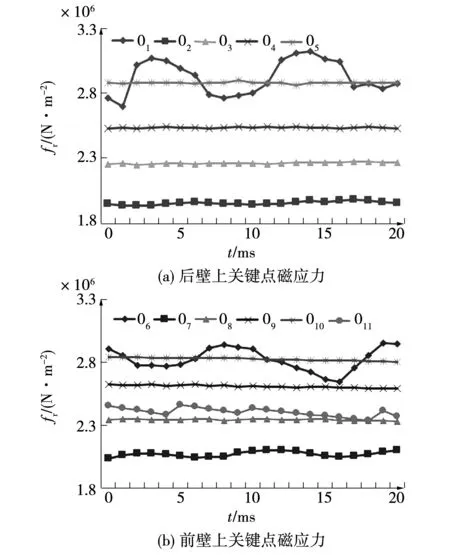
图8 转子1#齿上关键点磁应力Fig.8 Magnetic stress of key point in the 1# rotor teeth

当前壁关键点O1、O2取得最大值时，后壁相对的关键点O6、O7取得最小值。当前壁关键点O1、O2取得最小值时，后壁相对的关键点O6、O7取得最大值。关键点O3、O4、O5部分所受电磁力稍有下降趋势，后壁O8、O9、O10、O11所受电磁力稍有上升趋势，但整体波动不大。

汽轮发电机非全相运行后首周期内，3#小齿齿壁上关键点所受磁应力如图9所示。因为3#小齿所有关键点编号、位置及电磁力的正方向如图3(b)所示。

由图9可知，当变压器高压侧一相断开时，在汽轮发电机转子与大齿相邻的3#小齿前后齿壁所受磁应力分布不平衡。最接近齿顶面点O1所受电磁力波动最大，其受到的磁应力最大值为2.201×106N/m2，为与它最近关键点O2所受最大磁应力的1.531倍。关键点O6在后侧齿壁所有的关键点中最靠近齿面，它所受磁应力最大值为2.092×106N/m2，为和它最近关键点 O7的1.461倍，是该侧所有的齿壁上关键点所受最大磁应力的平均值1.082倍。

当前壁关键点O1、O2取得最大值时，后壁相对的关键点O6、O7取得最、小值。当前壁关键点O1、O2取得最小值时，后壁相对的关键点O6、O7取得最大值。关键点O3、O4、O5部分所受电磁力稍有下降趋势，后壁O8、O9、O10所受电磁力稍有上升趋势，但整体波动不大。

根据图8和图9可知，在时域内，磁应力随在转子小齿位置不同变化规律也各不相同。转子小齿一侧有浅槽时，小齿两侧齿壁所受磁应力较一侧无浅槽小齿大。在一个周期内，磁应力最大值的分布规律是: 在槽楔和阻尼条等高的小齿部分，小齿齿壁上关键点所受的电磁力较大，并且其所受的电磁力在时域内波动较大。而在励磁绕组部分等高的小齿部分，小齿壁所受电磁力由齿顶至齿底逐渐增大，并且其所受的电磁力在时域内波动越来越小，其后壁所受力稍有上升趋势，其前壁所受力稍有下降趋势，但整体趋于平稳。因此，在转子槽口、槽楔及阻尼条设计和各部分料选择方面，可考虑进行优化。

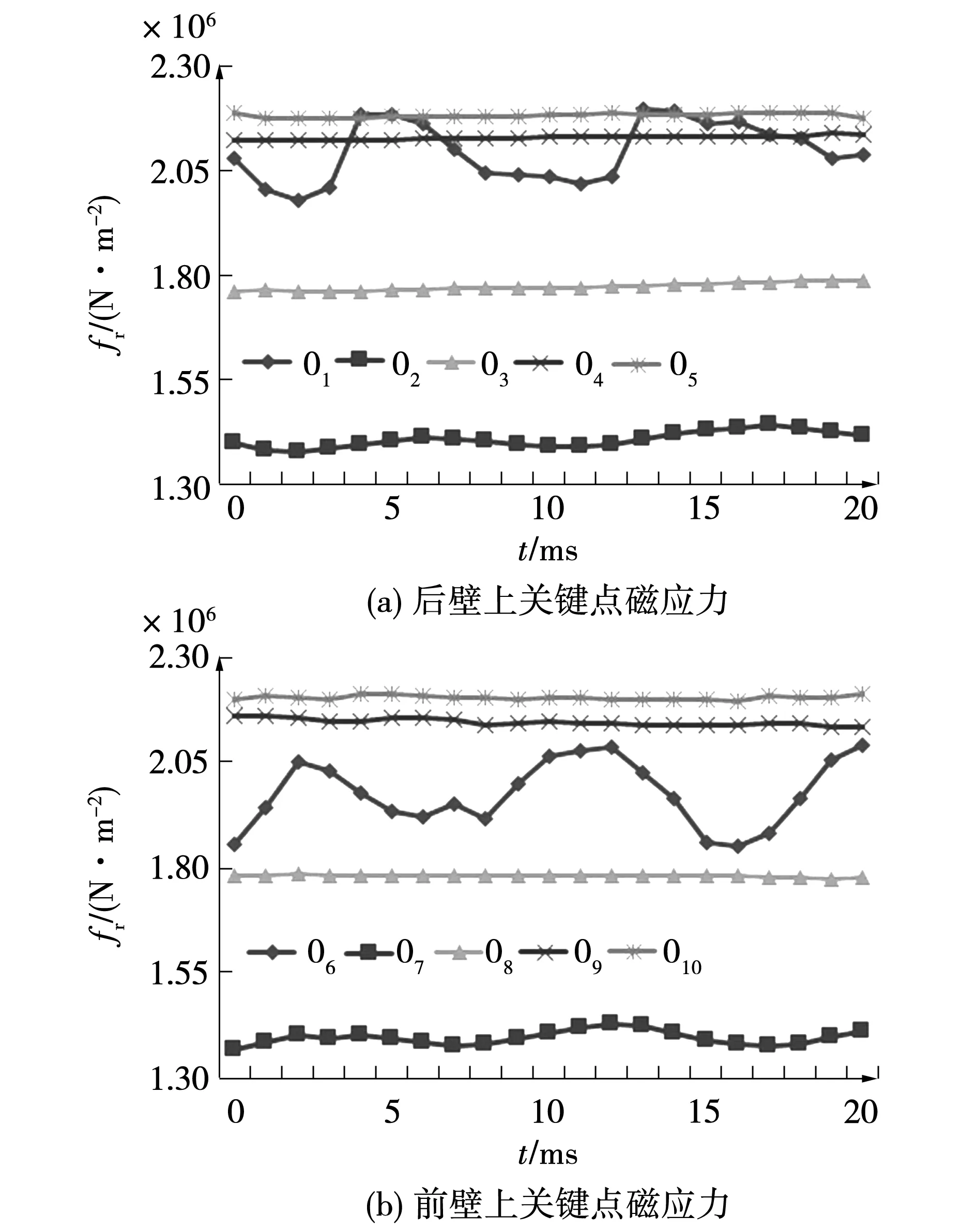
图9 转子3#齿上关键点磁应力Fig.9 Magnetic stress of key point in the 3# rotor teeth

为了与非全相运行相比，汽轮发电机额定运行时，转子1#齿、3#齿前后2个齿壁受力分布状况如图10所示，其中，横轴代表小齿齿壁所受磁应力，纵轴代表齿高。

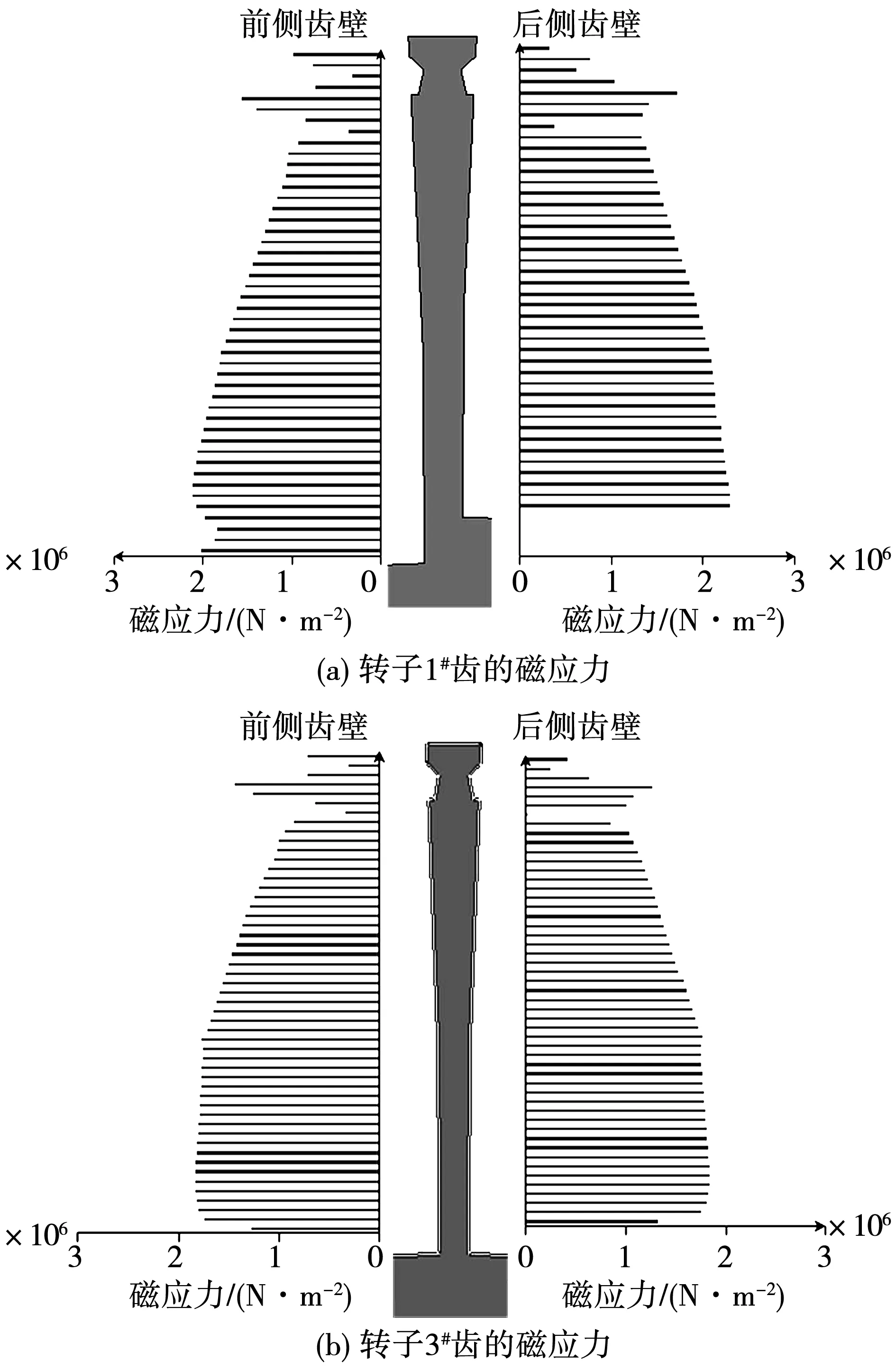
图10 额定运行时转子齿的磁应力分布Fig.10 Magnetic stress of the rotor teeth in the rated condition

由图10知，电机额定运行时，转子小齿前后两侧槽壁所受的磁应力方向相反，前侧受力方向与转子旋转的方向相同，与转子总的电磁转矩的方向相反；而后侧受力方向和转子旋转方向相反，与转子总的电磁转矩的方向相同。

在1#齿前后两侧齿壁上磁应力最大幅值分别为1.993×106、2.119×106N/m2。而电机非全相运行后首周期内，转子1#齿在前后侧相应位置磁应力最大幅值分别为额定运行时的1.472倍和1.479倍，3#齿前后两侧齿壁上磁应力最大幅值分别为1.839×106和1.836×106N/m2；而电机非全相运行后首周期内，3#齿前后侧相应位置的磁应力最大幅值分别为额定运行时的1.196倍和1.138倍。显然，非全相运行后首周期内，齿壁后侧磁应力是对形成电磁转矩起到主导作用的磁应力较额定时增强。

2.4 转子电磁力波计算

气隙磁场变化是研究电磁力波变化规律的基础，因此，针对非全乡运行的汽轮发电机，进行运用时步有限元模型计算磁场变化是首要工作。非全相运行后，汽轮发电机一个周期内典型时刻转子圆周上气隙磁密波进行谐波分析，得到典型次谐波幅值变化情况如图11所示。

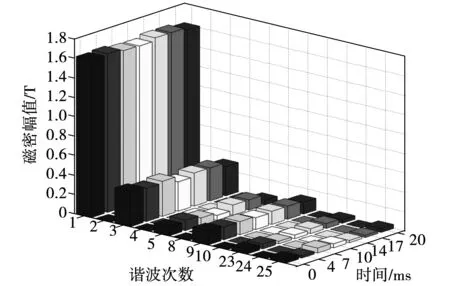
图11 气隙磁密典型时刻典型次谐波幅值Fig.11 Amplitude of typical harmonic of air gap flux density at the typical moments

由图11可以看出，断路故障发生后首周期内，1阶齿谐波中变化明显的为基波、5次、23次和25次谐波，它们的磁密幅值都增大。其中，基波磁密幅值最大为1.641 T，5次谐波磁密幅值最大为0.105 T，23次及25次谐波磁密幅值最大分别为0.0494 T与0.0508 T，磁密幅值下降的为3次谐波与9次谐波。

电机气隙磁场的波动影响电机转子经切向电磁力波变化规律，非全相运行后首周期内典型时刻转子切向和径向电磁力波变化情况分别如图12、图13所示。

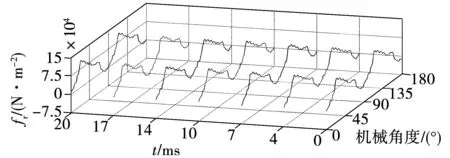
图12 非全相运行工况转子径向电磁力波变化Fig.12 Change of the radial electromagnetic wave of rotor under open-phase operation conditions

由图12、图13可以看出，非全相发生后，转子在第一个时间周期内受到的切向与径向电磁力波会发生畸变，且电磁力波幅值会有一定幅度的增加，表2、表3为具体不同时刻电磁力波的峰值。

由表2、表3结合图12、图13可以看出，非全相运行后转子受到径向力波正向最大幅值为正常时刻的1.05倍，力波负向最大幅值约为正常时刻的1.3倍，最小幅值为正常时刻的0.57倍。转子在切向方向上受到电磁力波同样发生较大变化，正方向的最大幅值为额定运行的1.32倍，负方向最大幅值为额定运行的1.04倍，负向最小幅值为正常时刻的0.76倍。由此可知，非全相运行后转子会受到反向电磁力较额定运行时波动较大，这一现象造成转子受到大小不均的扭转应力，非常容易使得转子部分区域受力不平衡，从而造成转子损坏等。

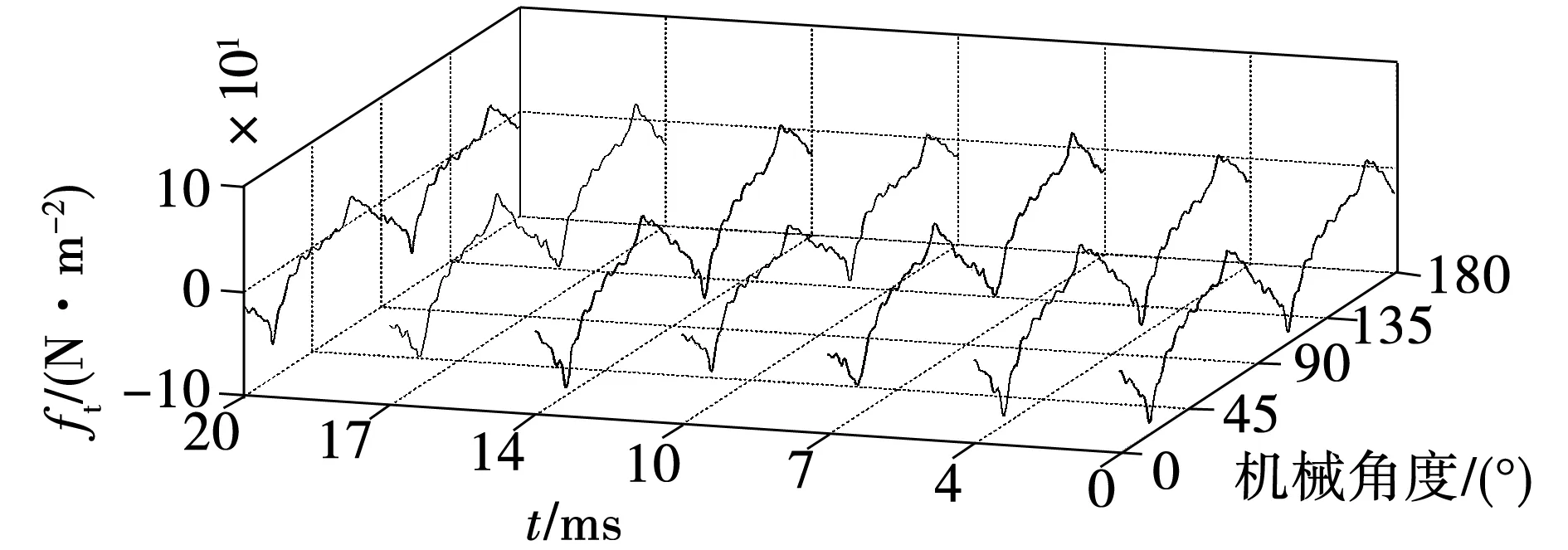
图13 非全相运行工况转子切向电磁力波变化Fig.13 Change of the tangential electromagnetic wave of rotor under open-phase operation conditions

表2 典型时刻径向电磁力波峰值

表3 典型时刻切向电磁力波峰值

3 结 论

本文建立了汽轮发电机非全相运行的场-路-网耦合仿真模型，运用麦克斯韦应力法，全面深入地分析了汽轮发电机非全相运行情况下转子局部动态电磁力的分布规律，主要结论为：

1)汽轮发电机发生非全相故障后首周期内，1/4周期时出现转子齿顶磁应力最大值，为2.278×106N/m2；且此时磁应力在汽轮发电机转子齿面上呈不对称分布，但不对称程度与额定运行时对比程度较大；此外，由于气隙附近的磁场变化最为剧烈，齿顶部的关键点受力较正常负载运行时变化明显。

2)非全相运行后，在转子槽楔和阻尼条等高部分小齿齿壁上关键点所受的电磁力较大，并且其所受的电磁力在时域内波动较大。而在转子励磁绕组部分等高部分小齿壁所受电磁力由小齿齿顶至小齿底沿径向逐渐增大，并且其所受的电磁力在时域内波动较小。其中，后壁所受力稍有上升趋势，前壁所受力稍有下降趋势，但整体趋于平稳。

3)非全相运行后，转子会受到反向电磁力波较额定运行时波动较大，这将对转子产生极大的波动扭转应力作用，极易造成转子局部受力不均。