部分核实数据下基于比例差的置信区间宽度的样本量确定

2021-06-10 07:30:06王黎明刘青松张晓良邱世芳

重庆理工大学学报(自然科学) 2021年5期

王黎明，刘青松，张晓良，邱世芳

（重庆理工大学理学院，重庆 400054）

研究某种疾病在人群中的流行率对生物医学相关研究具有重要意义，一般情况下通过判断受试者是否患有某种疾病对其进行分类从而获得该疾病的患病率。然而，在现实生活中，金标准检验无误判但价格昂贵，筛检方法价格低但常有误判。为了克服二者的不足，Tenenbein［1］提出了二重抽样的方法，即从总体中随机抽取N个个体利用筛检方法进行检验，再从N个个体中随机抽取n个个体接受金标准检验。这样，这n个个体同时接受了2种检验，而N-n个个体只接受了筛检检验，因此，Tang等［2］将采用二重抽样方法获得的数据称为部分核实数据。

在部分核实数据的研究方面，已有大量成果，例如文献［3-10］，但是上述研究都是基于有金标准分类器存在的情况下进行的。实际生活中，金标准分类器并不一定存在或可用，而无金标准存在的部分核实数据在实际生活中广泛存在。一个典型例子是Nedelman［11］利用二重抽样数据研究了疟疾的流行率，使用2种分类器（即初级显微镜者和高级显微镜者）对病人是否患有疟疾进行分类。由于无论是初级还是高级显微镜都存在误判，因而不存在金标准。表1列出了1个干旱季节和潮湿季节下2个年龄组（9～18岁，19～29岁）的疟疾数据。感兴趣的问题是：在不同的季节和不同的年龄组，疟疾的流行率是否有显著不同。为此，Qiu等［12］从齐性检验的角度进行了研究。然而，在医学研究中，需要多少个体参与试验也是一个重要的研究课题。Qiu等［13］从疾病流行率显著性检验的角度对样本量的确定进行了探究。Tang等［14］基于比例比，分别从假设检验与置信区间宽度的角度确定了近似样本量公式。然而，在给定置信水平下，关于疾病流行率之差（比例差）的置信区间的宽度控制在指定范围内的样本量确定还没有相关研究文献。因此，本文中将从置信区间宽度的角度出发对此问题进行研究，提出几种有效的样本量的确定公式或有效算法。如Nedelman［11］所论述，对此类问题假定不存在假阳性误判是合理的。因而，研究不存在假阳性误判下基于流行率之差的区间宽度控制下的样本量的确定问题。

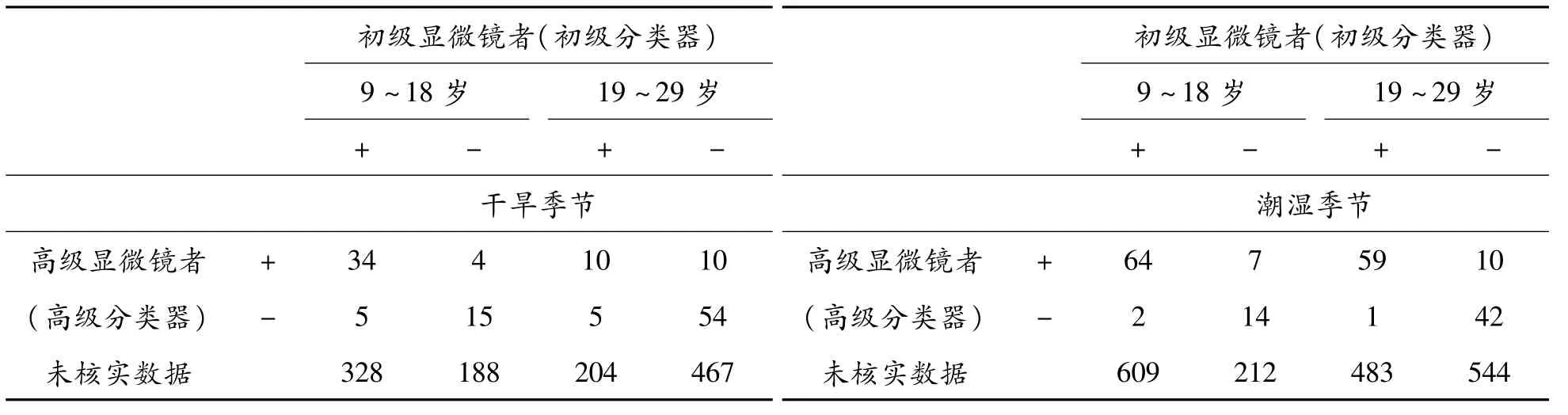
表1 疟疾数据

1 数据结构和统计模型

1.1 数据结构

假设有来自第j组的Nj个个体，对每个个体先用初级分类器进行检验，Jj=1表示阳性，Jj=0表示阴性。接着从Nj个样本中随机选取nj个个体再用高级分类器进行检验，Sj=1表示阳性，Sj=0表示阴性（j=1，2），数据如表2所示。

表2 二重抽样的数据类型

1.2 模型1的概率结构

表3 模型1的概率结构

设mj=（n11j，n10j，n01j，n00j，xj，yj），m=｛mj∶j=1，2｝，且π=（π1，π2），η=（η1，η2），θ=（θ1，θ2），则模型1下的似然函数为

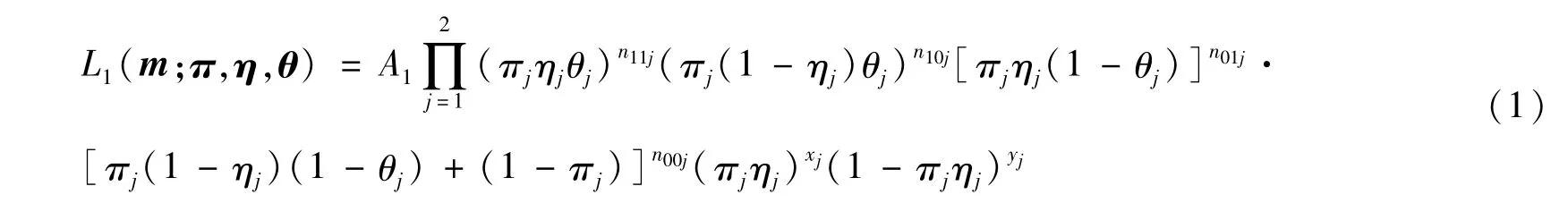
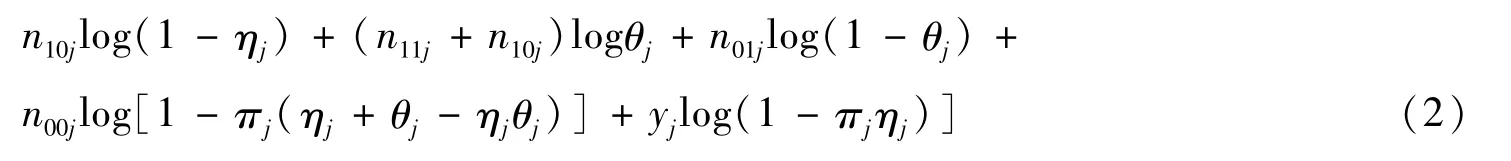
其中C1=log（A1）。根据文献［15］，当n11jn00j≥n10jn01j时，参数πj，ηj，θj的极大似然估计为

1.3 模型2的概率结构

在不假定条件独立性下，Lie等［16］在假定Pr（Jj=1，Sj=0|Dj=1）=Pr（Sj=0|Dj=1）、Pr（Jj=0，Sj=1|Dj=1）=Pr（Jj=0|Dj=1）下，提出了模型2，如表4所示。

表4 模型2的概率结构

模型2的似然函数为：

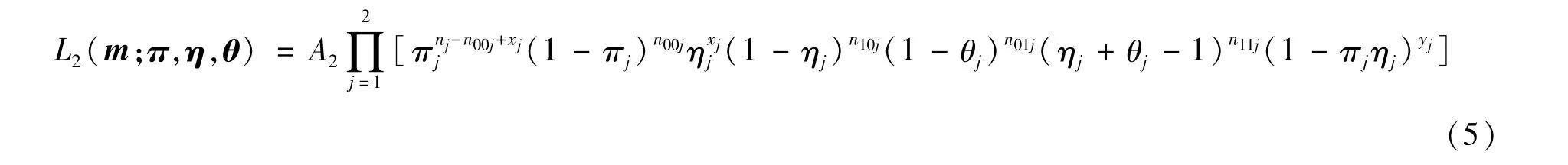
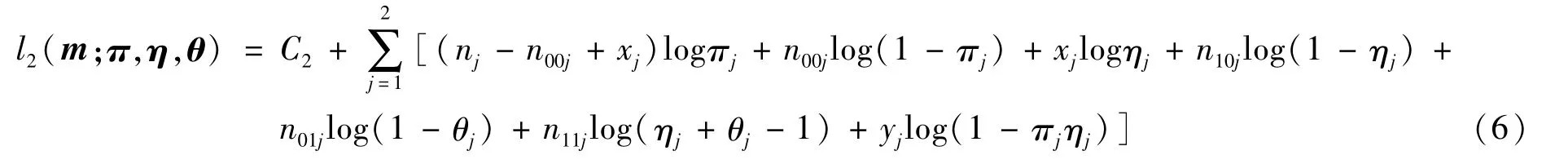
其中C2是与参数无关的常数。根据文献［15］，可得参数πj，ηj，θj的极大似然估计分别为

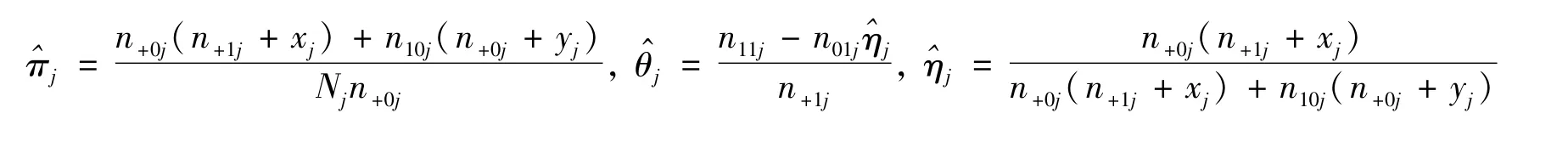
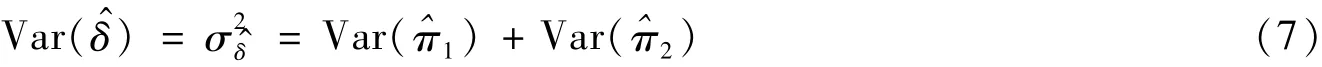
2 样本量的确定

假设核实验证比例为pj，即nj=Njpj，（j=1，2），并在N2=N1r下考虑样本量的确定问题。

2.1 基于Wald置信区间的样本量

基于以上得到的δ的估计和其估计的方差，易得到参数δ的基于Wald检验的置信水平为1-α的置信区间为：

其中，zα/2是标准正态分布的α/2分位数。为了将置信区间宽度控制在2ω以内，当ω≤δ时设否则由此可得置信区间宽度控制在指定宽度2ω所需的样本量为：

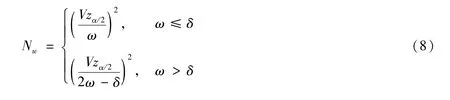
对于模型1：

对于模型2：

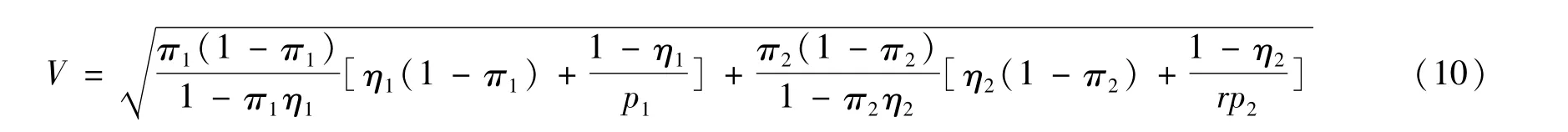
2.2 基于对数变换置信区间的样本量

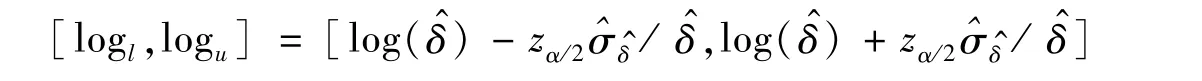
则δ的置信水平为1-α的置信区间为：

通过计算得到，基于对数变换的置信区间宽度控制在2ω所需的样本量为：

其中，模型1与模型2下，V分别由式（9）与（10）得到。

2.3 基于Logit变换置信区间的样本量

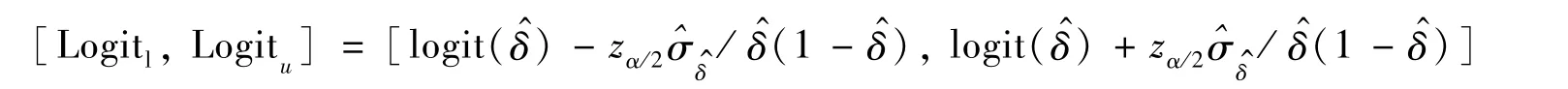
则δ的置信水平为1-α的置信区间为

通过计算可得基于Logit变换的置信区间宽度控制在2ω所需的样本量为

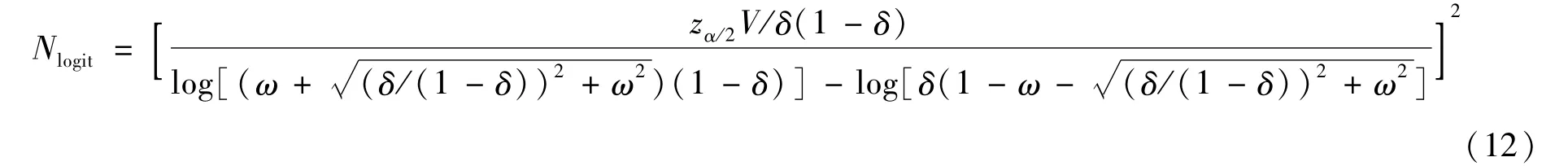
其中，模型1与模型2下，V分别由式（9）与（10）得到。

2.4 基于Score置信区间和似然比置信区间的样本量

由于基于Score和似然比检验统计量的δ的置信区间计算中需要参数π1，ηj，θj在δ=δ0下的限制性极大似然估计而这些估计没有显表达式，需要通过迭代算法得到，故考虑Zou等［17］提出的MOVER方法求得δ的置信区间。设δ的置信水平为1-α的置信区间上限δU和下限δL，根据中心极限定理易得：

同样，通过中心极限定理可直接求出πj（j=1，2）的置信水平为1-α的双边置信区间的上限uj和下限lj分别为：

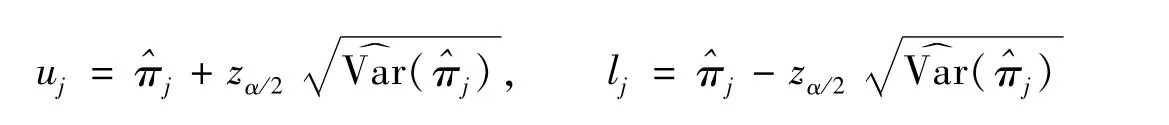
由此可得：

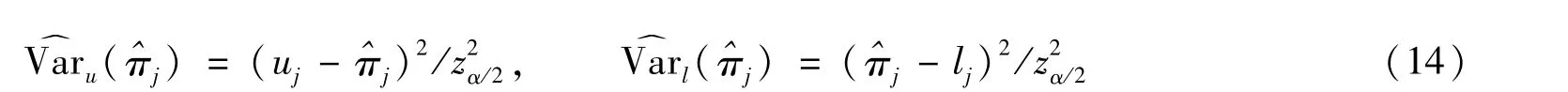
根据MOVER方法，下限δL的替换得到：

类似地，将上限δU的替换得到：

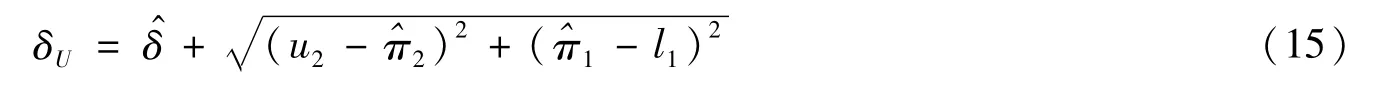
分别基于以下的Score检验统计量与似然比检验统计量求得πj（j=1，2）的置信水平为1-α的双边置信区间的上限uj和下限lj，代入上述δL和δU的式中，从而得到δ的置信水平为1-α的置信区间。

2.4.1 基于Score检验统计量的置信区间

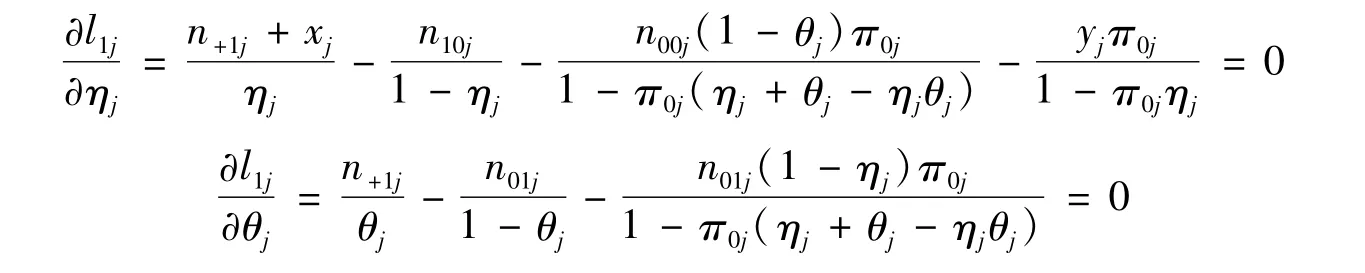
上述方程组无显式解，可通过迭代算法求得。

在模型2下：

基于Rao［18］的理论，在模型1下，检验假设H0j∶πj=π0j的Score检验统计量为

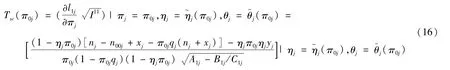
在模型2下：

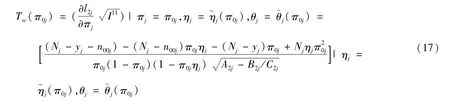
根据文献［19］，当nj→∞时，在H0j下Tsc（π0j）渐近服从标准正态分布，利用迭代方法解如下方程可得到基于Score检验统计量的置信水平为1-α的πj置信区间上限与下限为

2.4.2 基于似然比检验统计量的置信区间

在模型1下，检验假设H0j∶πj=π0j的似然比检验统计量为

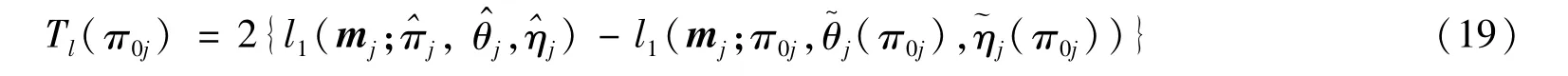
在模型2下，检验假设H0j∶πj=π0j的似然比检验统计量为

根据文献［20］，似然比检验统计量Tl（π0j）渐近服从自由度为1的卡方分布，通过解方程Tl（π0j）=可得到基于似然比检验统计量的置信水平为1-α的πj置信区间上下限。

2.4.3 样本量的数值解法

由于基于以上检验统计量Tsc（π0j）和Tl（π0j）计算的πj置信区间均没有显表达式，采取如下的搜索算法来获得近似样本量的估计：

步骤1给定π1，ηj，θj，δ，r，pj，N1的值，产生K组随机样本mj=（n11j，n10j，n01j，n00j，xj，yj）。

令M（·）表示多项分布，在模型1下，（n11j，n10j，n01j，n00j）～M（nj；πjηjθj，πj（1-ηj）θj，πjηj（1-θj），πj（1-ηj）（1-θj）+（1-πj））。

在模型2下，（n11j，n10j，n01j，n00j）～M（pjNj；πj（ηj+θj-1），πj（1-ηj），πj（1-θj），（1-πj））。

两种模型下（xj，yj）都服从二项分布B（（1-pj）Nj，πjηj）。

步骤2基于步骤1产生的样本，结合MOVER方法计算δ的置信区间。并通过K个置信区间宽度的平均值计算近似的区间宽度，记为2ω*（N1）。

步骤3若2ω*（N1）大于（小于）2ω，则增加（减少）N1的值，重复步骤1、2。

步骤4重复步骤3直到近似的半区间宽度ω*（N1）非常接近于给定的区间宽度ω，则N1=min｛N1∶|ω*（N1）-ω|≤0.001｝即为满足条件的近似样本量。

通过以上搜索方法可获得基于Tsc（π0j）和Tl（π0j）的置信区间的样本量Nsc和Nl。

3 模拟研究

对于模型1和模型2下所提出的样本量的估计方法，通过计算在估计的样本量下δ的置信区间的经验覆盖概率（ECP）和经验覆盖宽度（ECW）来评估本文中所提出方法的有效性。1）经验覆盖概率（ECP）

［δL（m（k）），δU（m（k））］为δ的第k个置信区间，：j=1，2｝，此时I｛δ∈［δL（m（k）），δU（m（k））］｝为示性函数。

2）经验覆盖宽度（ECW）

在置信水平1-α=0.95下分别通过以下参数设置考察了各种样本量估计方法的有效性：

1）δ的影响。为研究δ的变化对样本量的影响，在2种模型下，考虑如下参数设置：δ=0.1（0.01）0.3，π1=0.3，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1以及（a）：r=1.0，p1=p2=1/3，（b）：r=2.0，p1=p2=1/3，（c）：r=1.0，p1=1/3，p2=1/5，（d）：r=2.0，p1=1/3，p2=1/5。图1、3给出了估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW。对于模型1和模型2，随着δ的逐渐增大，基于所有方法计算的所需样本量均逐渐增加，基于对数变换置信区间的样本量Nlog和基于Logit变换置信区间的样本量Nlogit相对其他3种方法较小，所有方法的ECP均接近于事先给定的置信水平1-α=0.95，ECW接近于2ω=0.2。

2）p1和p2的影响。为研究p1的变化对样本量的影响，考虑如下参数设置：p1=0.1（0.1）0.9，π1=0.3，δ=0.2，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1，p2=0.3，（a）：r=1.0，（b）：r=2.0。为研究p2的变化对样本量的影响，考虑如下参数设置：p2=0.1（0.1）0.9，π1=0.3，δ=0.2，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1，p1=0.3，（c）：r=1.0，（d）：r=2.0。图2、4给出了估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW。模拟研究结果表明，随着p1和p2的增大，基于所有方法计算得到的样本量均减少，所有方法的ECP均接近于事先给定的置信水平1-α=0.95，ECW接近于2ω=0.2。

图1中，δ=0.1（0.01）0.3，π1=0.3，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1。

图1 模型1：置信水平1-α=0.95下，估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW随δ变化的情况

图2中，π1=0.3，δ=0.2，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1。

图2 模型1：置信水平1-α=0.95下，估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW随p1、p2变化的情况

图3中，δ=0.1（0.01）0.3，π1=0.3，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1。

图3 模型2：置信水平1-α=0.95下，估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW随δ变化的情况

图4中，π1=0.3，δ=0.2，η1=θ1=0.8，η2=0.85，θ2=0.75，ω=0.1。

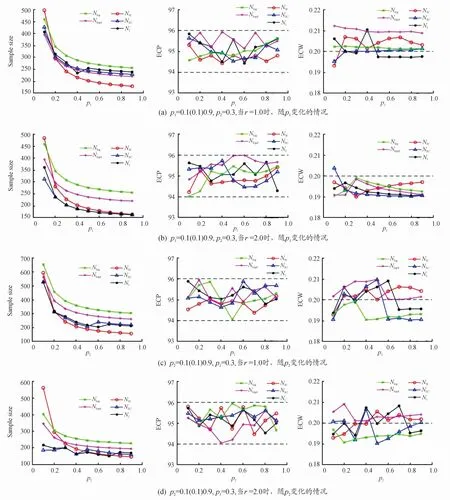
图4 模型2：置信水平1-α=0.95下，估计的样本量N1、置信区间的经验覆盖概率ECP（%）和经验覆盖宽度ECW随p1、p2变化的情况

4 实例分析

采用所提出的方法对表1数据进行分析。表5列出了2个调查组下不同年龄组患病率之差δ、2组年龄下不同调查组患病率之差δ的参数估计，置信水平1-α=0.95下区间宽度控制在区间宽度ω=0.1下的样本量估计，在估计样本量下δ的置信区间的经验覆盖概率和经验覆盖宽度。结果表明：对于模型1，基于对数变换方法的ECW相对于其他4种方法较小，在模型2下则相反。值得注意的是，在模型1与模型2下，基于Wald方法置信区间得到的样本量明显大于其他4种方法的样本量，但所有方法的ECP均接近于事先给定的置信水平1-α=0.95，ECW接近于2ω=0.2，现有样本量满足实验需求。

5 结论

基于无金标准的部分核实数据，从比例差的区间宽度的角度给出了比较2组患病率是否有显著性差异所需要的样本量。在2种不同二重抽样模型下，给出了在给定置信水平下置信区间宽度控制在指定范围内的样本量估计公式。模拟结果表明：相同参数设置下模型1下各种方法所需样本量大于模型2下相应方法所需的样本量；在2种模型下，基于所提出的各种方法估计的样本量下计算的δ的置信区间的经验覆盖概率接近给定的置信水平且经验覆盖宽度接近设定的宽度。由此可知，所提出的样本量估计公式和数值算法有效，推荐在实际应用中使用。

附录：Fisher信息阵

令Ij=（Ilkj）3×3表示第j组下2个模型的费希尔信息矩阵，其中，在模型1下，

在模型2下