基于果蝇优化算法的无人机航路规划方法

张国印，孟 想，李思照

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨150001)

0 引言

无人机静态航路规划是指根据已知的地图信息和威胁因素，离线规划出一条连接起点和终点的代价最小的全局路径。

果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)是潘文超在2012年提出的一种新型生物启发算法[1]，FOA不仅能够非常有效地解决复杂的优化问题，而且拥有更少的参数和更小的计算成本[2]。自推出以来，FOA已被广泛应用于科学和工程领域，并与其他数据挖掘技术相结合，如优化机器学习算法，提高人脸识别系统的识别率、特征选择、培训风险评估模型以及预测空闲停车位的可用性[3]。

FOA算法操作简单、搜索能力强，但也存在后期进化过程中过早收敛和收敛速度慢等缺点。为了克服这些缺点以及提高全局搜索能力，研究人员已经对果蝇优化算法提出了各种改进和变体。IFFO算法[4]引入了一个新的参数来控制果蝇群体，使其能够自适应地调整搜索范围，并引入了一种新的解生成方法来提高精度和收敛速度。在MFOA[5]中，多个子群可以同时在搜索空间中独立移动，并且利用子群之间的局部行为规则来探索全局最优。所有这些改进的FOA变种在一定程度上成功克服了原始FOA的缺点。然而，在收敛速度或避免陷入局部最优方面，特别是对于处理复杂的实际问题方面，仍然有很大的改进空间。

本文提出了一种基于果蝇优化算法的静态航路规划方案。针对上述FOA的不足，在基础FOA的基础上，从3个方面提出改进：① 采用混沌初始化，减少初始参数对解的影响，提高FOA的稳定性；② 自适应调节果蝇步长，提高算法精度；③ 引入模拟退火策略，使FOA可以有效避免陷入局部最优。使用改进后的FOA进行无人机静态航路规划，最后验证算法在无人机航路规划中的合理性和有效性。

1 果蝇优化算法介绍

果蝇优化算法的灵感来源于果蝇的觅食行为，由于其拥有突出的嗅觉和视觉，在觅食的过程中，果蝇可以利用嗅觉器官感知空气中漂浮的食物味道，判断出食物的大致方向，然后向该位置飞近。随后，其他果蝇会利用视觉器官感知最优果蝇的位置，并向其飞去。果蝇群体的食物搜寻过程如图1所示，整个觅食的过程就是一个不断迭代求取最优值的过程。

图1 果蝇觅食过程Fig.1 Group iterative food searching process of the fruit fly swarm

根据果蝇的觅食特点，果蝇优化算法大概可以分为以下3个阶段。

(1) 参数和种群位置初始化

FOA的参数包含种群大小Mosp和最大迭代次数Gmax。首先，在决策空间中随机初始化果蝇群位置(Xaxis,Yaxis)，如式(1)所示。

(1)

式中，rand()是生成[0,1]之间均匀随机数的函数。

(2) 基于嗅觉的搜索

在基于嗅觉搜索的过程中，随机分配果蝇个体搜索食物的距离与方向，搜索策略如式(2)所示。

(2)

式中，i=1,2,…,Mosp，random是范围为[-1,1]之间的随机值。

食物的准确位置未知，因此需要先计算出果蝇个体与原点之间的距离Dist，再计算味道浓度判定值S，此值是Dist的倒数，如式(3)所示。

(3)

实际上，味道浓度的判断对应于决策空间中目标函数的候选解，因此，将S带入目标函数，可以求出该果蝇个体此时所处位置的味道浓度，计算如式(4)所示。

Smelli=f(Si)。

(4)

(3) 基于视觉的搜索

基于视觉的果蝇群体搜索过程本质上就是一个贪婪选择的过程，果蝇群通过观察上述基于嗅觉搜索过程生成的所有位置，找出气味浓度最佳的位置并记录该位置的下标，如式(5)所示。

index=argmin(Smelli)。

(5)

果蝇群体会利用视觉向新位置飞去。基于视觉的搜索过程可以描述成式(6)。

(6)

最后，重复基于嗅觉和视觉的搜索过程，直到达到最大迭代次数或找到最优解。

2 基于果蝇优化算法的无人机航路规划

2.1 基于B样条曲线的航路表示

无人机无法直接实现“急转弯”，直接转换方向进入下个航段，因此需要对存在夹角的航路进行平滑处理，使平滑后的航路能够满足无人机的物理转弯性能，即要大于无人机的最小转弯半径。B样条曲线是目前应用比较广泛的航迹平滑算法。

一般采用二次B样条曲线进行航路平滑，下面详细介绍应用于平滑航路的B样条曲线的曲率表达式推导过程[6]。每一段二次B样条曲线参数方程如式(7)和式(8)所示。

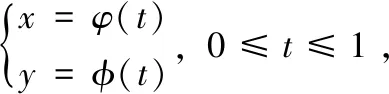
(7)

(8)

对式(7)求导得到式(9)和式(10)：

(9)

(10)

式中，a=x02x1+x2，b=x1-x0，c=y0-2y1+y2，d=y1-y0。由曲线曲率公式可以得到曲率k，如式(11)所示。

(11)

曲线的曲率半径r为曲率的倒数。当r大于无人机最小转弯半径时，则认为无人机满足飞行约束条件。

B样条函数具有连续的一阶导数和二阶导数，并且其曲率在转弯点变化均匀，符合无人机速度和加速度连续变化的要求，生成的航路曲线更加平滑，也解决了转弯点大角度控制问题。

2.2 无人机自身性能约束

(1) 最低飞行高度

无人机在进行飞行的过程中需要保持一定海拔高度，飞行高度过低可出现撞击地面的风险。采用Hmin表示物流无人机的最低飞行高度，则每一段航路的飞行高度Hi(i=1,2,…,n)，需满足:

Hi≥Hmin。

(12)

(2) 最小航段长度

最小航段长度是指无人机在调整飞行姿态前必须保持的最小直线飞行距离。用Lmin表示物流无人机的最小航段长度，Li(i=1,2,…,n)表示物流无人机第i个飞行航段的长度，则该约束可以表示为:

(13)

其中，(xi,yi,zi)为航迹点i的三维空间坐标，(xi-1,yi-1,zi-1)为航迹点i-1的三维空间坐标。

(3) 最大航程约束

无人机在执行任务时，由于物理性能、燃料量以及快件配送时效性等因素，需要对无人机的最大航程加以约束。最大航程总长为每个航段长度之和，用Lmax表示最大航程，则该约束可以表示为:

(14)

(4) 最大偏航角

偏航角限制也是最小转弯半径限制，转弯角越小无人机就越能平稳飞行。假设无人机允许的最大偏航角是θ，最大偏航角示意如图2所示。

图2 最大偏航角示意图Fig.2 Schematic diagram of maximum yaw angle

图中，Pi-1，Pi，Pi+1分别表示第i-1，i，i+1个航迹点，坐标值分别是(xi-1,yi-1)，(xi,yi)，(xi+1,yi+1)，航路段i的水平投影为ai=(xi-xi-1,yi-yi-1)，航路段i+1的水平投影为ai+1=(xi+1-xi,yi+1-yi)，则该约束可以表示为:

(15)

(5) 最大俯仰角

最大俯仰角是指无人机在垂直方向上爬升和俯冲的性能约束限制，主要是为了降低无人机发生碰撞和坠机的风险。假设无人机允许的最大俯仰角为φ，航迹段i的纵向高度差为|zi-zi-1|，则该约束可以表示为：

(16)

2.3 航迹评价指标

本文主要研究的代价包括航程代价、高程代价和威胁代价。代价函数表示方式为：

Fcost=ω1fL+ω2fH-ω3fT，

(17)

式中，fL为每段航路的航程代价，fH为高程代价，fT为威胁代价，ω1，ω2，ω3为各个航路代价指标的权重，满足ω1,ω2,ω3≥0且ω1+ω2+ω3=1，通过调整权重的取值，可以实现使某项代价指标为航路代价的主要影响因素，体现航路规划的灵活性，为综合决策提供参考。

(1) 航程代价

航程代价需要考虑从航迹点到目标点的飞行距离，设fL为航程代价，起始点S为第0个航迹点，某段航路共有m个航迹点，则该航路的航程代价可表示为：

(18)

式中，di,i+!表示两个相邻航迹点之间的距离。

(2) 高程代价

高程代价表示无人机由当前航迹点飞向下一个航迹点处于的海拔高度所需要的做功值。无人机飞行高度越大，代价越大；反之，代价越小。设fH为高程代价，则该航路的高程代价可表示为：

(19)

式中，M为无人机在负载情况下的整机质量，是无量纲的可变常量，hi为航迹点i的海拔高度，g为重力加速度，取值为10。

(3) 威胁代价

威胁代价考虑地形、天气威胁以及禁飞区危险性各代价的总和，设fT为威胁代价，共有λ个威胁，第k个威胁的中心平面坐标为(xk,yk)，则威胁代价可表示为：

(20)

2.4 果蝇优化算法在航路规划中的应用

在基于FOA做无人机航路规划的过程中，FOA被用来生成连接给定起点和终点的具有最小代价函数值的B样条曲线。

B样条曲线的形状由无人机起点和终点之间的一些可以自由移动的控制点来决定，把曲线控制点的笛卡尔坐标作为果蝇群体的食物来源。假设自定义控制点的数量为n，那么在规划航路的过程中需要确定D=3n个坐标参数，即{x1,x2,…,xD}，其中(xi,xn+i,x2n+i),i=1,2,…,n为航路曲线第i个控制点的三维坐标。

设置每个果蝇的位置代表一个控制点的坐标，这样果蝇群体的所有位置都可以表示一条飞行路径。通过FOA所得到的每条候选路径都由代价函数来进行评估。假设无人机飞行航路的任务空间限制在[0,Lmax]×[0,Wmax]，最大飞行高度为Hmax，在FOA第t次迭代时，第i只果蝇的位置由坐标(Xi,1,Xi,2,…,Xi,D)和(Yi,1,Yi,2,…,Yi,D)表示，对应的控制点序列由(Si,1,Si,2,…,Si,D)表示，无人机飞行代价函数作为FOA气味浓度判断函数。将FOA应用于无人机路径规划的具体实现过程如算法1所示。

算法1 基于FOA的航路规划伪代码

3 基于改进果蝇优化算法的无人机航路规划

3.1 果蝇优化算法改进策略

3.1.1 混沌初始化

混沌理论是指在一个完全被数学公式精确描述的确定系统中，即便没有外部因素的干扰，系统的运行也可能变得无法预测。混沌理论具有内在随机性，会产生与外界因素干扰完全无关的系统内部自发性的自组织现象。混沌理论的另一个特性是初值敏感性，这种特性会对系统运动趋势产生强烈影响，并且会使系统长期行为变得不可预见[7]。

FOA的运行结果高度依赖于初始条件，初始条件的微小差异将会对最终结果产生重大的影响，本文采用Logistic混沌映射来处理初始参数，以提高FOA的稳定性。

Logistic映射是混沌系统行为的一个经典模型，本质上是一个时间离散的动力系统，即按照式(21)进行反复迭代。

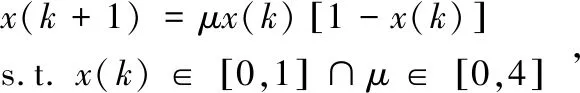
(21)

式中，k为当前迭代次数，μ为混沌控制参数，当x(k)∈[0,1]并且μ=4时，上述系统处于完全混沌状态，混沌变量Cx(k)可以表示为:

Cx(k+1)=4Cx(k)[1-Cx(k)]。

(22)

如果所求问题满足xi∈[li,ui]，li和ui分别代表变量取值范围的下界和上界，那么其与混沌变量之间可以由式(23)和式(24)进行往返映射。

Cx(i)=(xi-li)/(ui-li)，

(23)

xi=li+Cx(i)(ui-li)，

(24)

式中，xi表示第i个混沌变量经过混沌映射变换后转换为常规变量的值。

本文基于混沌变量的遍历性，使用logistic映射对果蝇群的初始位置进行赋值，降低在搜索最优解时初始条件的敏感性。具体过程如下：

步骤1：首先随机生成3个M维向量Cx1=(x1,x2,…,xM)，Cy1=(y1,y2,…,yM)和Cz1=(z1,z2,…,zM)，任意分量取值在[0,1]之间。

步骤2：分别将Cx1，Cy1，Cz1带入式(21)，得到Cx2，Cy2，Cz2，再将Cx2，Cy2，Cz2带入式(22)，循环计算，直到迭代次数达到300。

步骤3：将步骤2中得到的300个混沌变量Cxi，Cyi，Czi(i=1,2,…,300)，根据式(23)映射到算法的规划空间中，并以此计算目标函数值，从中选取出较优的Mosp个向量作为果蝇群的初始位置。

其中，M表示求解问题的维度，μ=4，为保证遍历的充分性，混沌序列取值点数要大于等于300。

经过上述过程的初始化后，果蝇群的初始位置相较于随机分配具有一定的优势，降低了随机初始化对果蝇群搜索最优解的不良影响，一定程度上提高了算法的求解性能。

3.1.2 自适应步长

在基本FOA中，果蝇在迭代过程中的步长是预设的固定值，若步长取值较大，随着多次迭代的完成，当果蝇群体距离目标越来越近时，局部搜索会有限制，会导致求解精度的下降；若步长取值较小，虽然可以做到局部深度搜索，但是搜索的效率和速度都会大幅下降，甚至可能无法求得最优解。因此，将果蝇群迭代过程中的固定步长调整为线性递减的自适应步长，以提高算法的精度，避免陷入局部最优。步长自调整过程如式(25)所示。

(25)

式中，stept为第t次迭代的步长，Gmax为最大迭代次数，α为步长调节因子，当α取值不同时，步长变化速率也不同，此处取α=0.1。当Gmax取值100，step的初始值取1时，stept的数值变化曲线如图3所示。

图3 步长变化曲线Fig.3 Step change curve

由图3可知，随着迭代次数t的增加，stept单调递减，因此果蝇移动的步长可以随着迭代次数的增长而自适应变小。将自适应步长变化带入果蝇基于嗅觉的搜索过程，如式(26)所示。

(26)

综上所述，使用自适应策略调整果蝇在迭代过程中的步长大小，可以使步长随着迭代次数的增加而减小，这样不仅满足算法在运行初期时需要采用大步长进行全局搜索，又满足在算法迭代后期需要采用小步长进行局部深度搜索，可以有效控制FOA的收敛速度，增加算法的求解精度。

3.1.3 模拟退火策略

模拟退火算法(Simulated Annealing Algorithm,SA)最早是由N.Metropolis等于1953年提出[8]，其出发点是模仿经典粒子系统降温的过程来寻找问题的极值，从而优化求解过程。对于温度T的每一个取值，都需要采用Metropolis[9]准则进行判断，依概率决定是否跳出。

Metropolis准则是SA的核心部分，通常表示为:

(27)

式中，Ej为新状态的能量，Ei为当前状态的能量，在改进算法中对应的是相应目标函数。当m>[0,1)区间的随机数时接受跳出，否则不接受跳出。i为当前状态，j为新状态，T表示温度，则“跳出概率”p的表达式为:

(28)

当新状态的能量比旧状态能量低时，跳出概率为1；当新状态的能量比旧状态能量高时，不会立刻舍弃Ej，而是进行概率判断，将m与随机数ε(0≤ε<1)比较，当m>ε时，同样跳出，否则舍弃Ej。由于Ej-Ei与T的值是变动的，因此这个概率是一个动态概率。

在FOA基于视觉搜索的过程中，所有的果蝇个体都会向当前最优个体的方向飞去，如果当前最优个体陷入局部极值，基本FOA没有策略可以帮助果蝇跳出极值，果蝇将停止继续进化，算法寻优过程将以失败告终。为了解决这一问题，本文采用了模拟退火策略，结合SA策略的视觉搜索具体流程如下：

步骤1：根据FOA算法实现过程，保留本次迭代果蝇群中最优味道浓度的果蝇，记为S(i)，同时记录该果蝇的位置坐标(Xi,Yi)，S(i)为当前模型。

步骤2：确定初始温度T0=S(i)/lg(5)。

步骤3：用式(25)和式(26)对当前位置(Xi,Yi)进行一定次数的扰动，得到新的模型S(i)′，位置坐标为(X′i,Y′i)。

步骤4：采用模拟退火策略，计算新旧模型的差值Δs=S(i)'-S(i)：若Δs≤0，则S(i)′被接受。若Δs>0，则计算概率p=epx(-Δs/T)，若p>ε，ε为[0,1]之间的随机数，则S(i)′被接受，并以(X′i,Y′i)开始下一次的迭代寻优；否则以原模型的位置坐标进行下一次迭代寻优。

步骤5：利用T=T0×0.5进行退温操作。

由于SA有一定概率可以接受较差解，所以当果蝇在陷入局部极值后可能跳出，部分果蝇可以飞向其他方向，这部分果蝇可能具备更强的全局搜索能力，搜寻到更佳的全局最优解。因此，引入模拟退火策略在一定程度上解决了FOA容易陷入局部最优的问题，对于求解多极值问题，引入模拟退火机制的FOA更具优势。

3.2 改进果蝇优化算法在航路规划中的应用

在FOA的基础上，本文引入了混沌初始化、自适应步长和模拟退火三个策略，形成了基于混合策略的果蝇优化算法，结合求取极大值问题，该算法运行步骤如下：

步骤1：初始化算法相关参数，并采用混沌策略设置果蝇群初始位置(Xaxis,Yaxis)。初始化参数包括估果蝇种群规模Mosp，最大迭代次数Gmax，初始温度T0，步长初始值step0等。令当前迭代次数t=0。

步骤2：遍历每一只果蝇，依次计算果蝇个体与原点之间的距离Dist，味道浓度判定值S和味道浓度Smell。

步骤3：找出本次迭代过程中味道浓度最好的个体，保留味道浓度值和该个体对应的位置坐标。

步骤4：利用自适应步长公式对最佳位置的果蝇进行混沌局部扰动，依据Metropolis接受准则，选取本次迭代过程中的最优味道浓度值和下次寻优的初始位置。

步骤5：更新全局最优值。如果本次迭代得到的最优值优于全局最优值，那么更新全局最优值，否则保持不变。

步骤6：进入迭代寻优。进行退温操作，令k=k+1，重复步骤2～步骤5，直到寻得最优解或者到达最大迭代次数。

前面已经讨论过基本FOA在无人机航路规划过程中的应用，本节将给出改进后FOA在无人机航路规划过程的应用流程。基于改进FOA在无人机航路规划中的应用流程如算法2所示。

算法2 基于改进FOA的航路规划伪代码

4 仿真实验与结果分析

为验证算法的有效性，本文在Windows10-Intel(R)Core(TM)i5-8250U CPU @ 1.60GHz 1.80GHz-16GB八核处理器-64bit PyCharm平台上进行仿真。将在同一场景下测试5种算法，包括本文提出的多策略融合FOA、基本FOA、文献[4]提出的IFFO、粒子群算法(PSO)以及差分进化算法(DE)。

4.1 实验参数

本文构建10 km×10 km×0.2 km的三维空间，已知地形和威胁如图4所示。

图4 等效数字地图仿真Fig.4 Equivalent digital map simulation map

仿真实验中对物流无人机的物理约束条件规定和航迹评价指标权重值参数设置如表1所示。

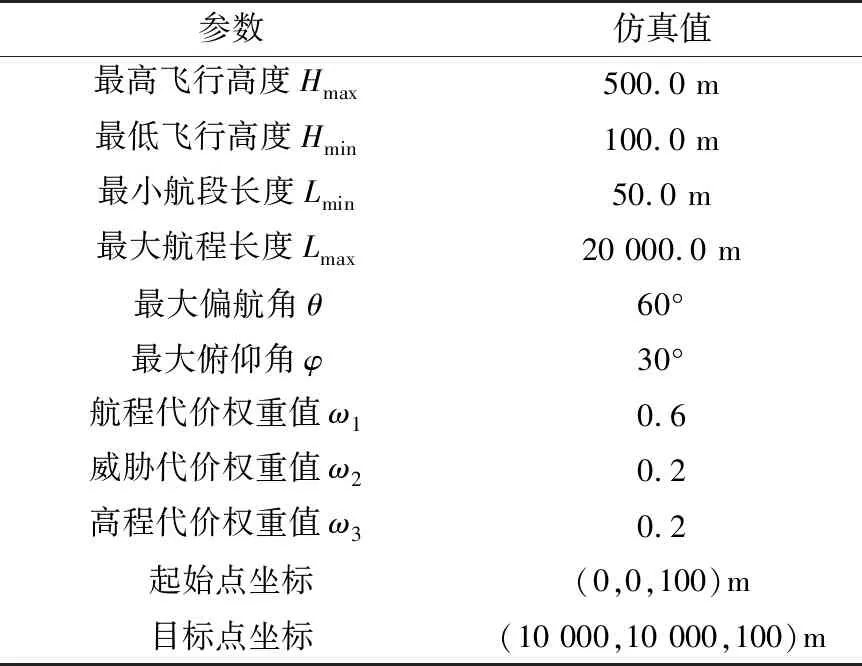
表1 仿真参数

5种测试算法的主要参数如表2所示。为了进行公平的比较，所有算法都使用相同的最大迭代次数作为停止标准，所有算法的种群大小都设置为50。

表2 算法控制参数

4.2 实验结果分析

图5展示的是5种算法进行50次独立运行所得到的最优路径在xoy平面上的投影，图6展示了5种测试算法得到的最佳无人机航路的飞行高度变化曲线。

从图5和图6可知，大多数算法都成功找到可以避开所有威胁区域的安全航路，但是在图5中，可以明显看出由DE生成的航路是一条不完整的曲线，这是因为DE规划的航路进入了威胁区域。图7展示了5条航路对应的三维立体图，分别对应的是改进FOA、基本FOA、IFFO、PSO和DE。

由图7可知，改进FOA可以生成具有威胁规避和地形跟随特性的无人机航路，从而提高物流无人机的生存能力和执行配送任务的有效性。表3展示了5条最佳航路的航程、规划耗时以及代价值等数据结论，从中可以看出改进FOA在5种测试算法中生成的路径最短，基本FOA生成的路径最长，IFFO生成的航路长度虽然和改进FOA生成的航路长度相近，但由图7可以看出，IFFO多是进行高程避障，而无人机在执行任务时，应尽量避免采用高程避障。

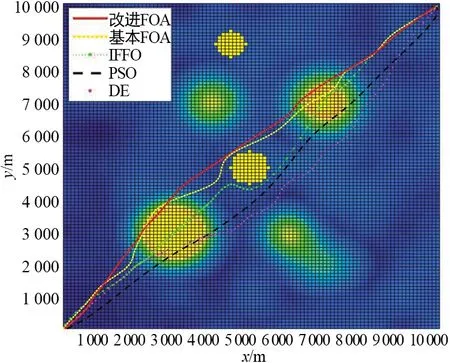
图5 最优航路xoy平面投影Fig.5 Plane projection of optimal route

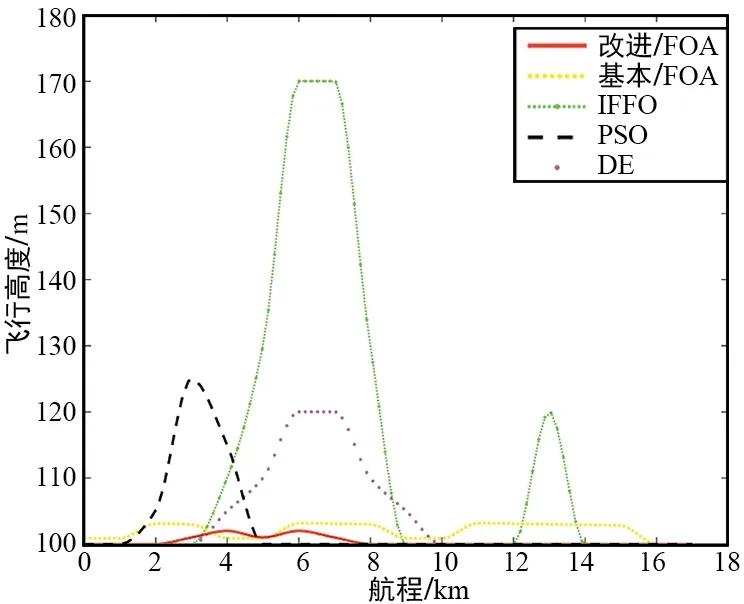
图6 最优航路高程变化曲线Fig.6 Optimal route elevation change curve

(a) 改进FOA最优航路

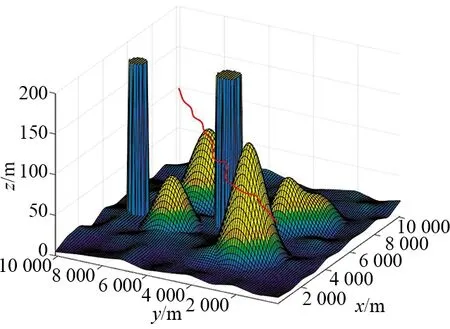
(b) FOA最优航路

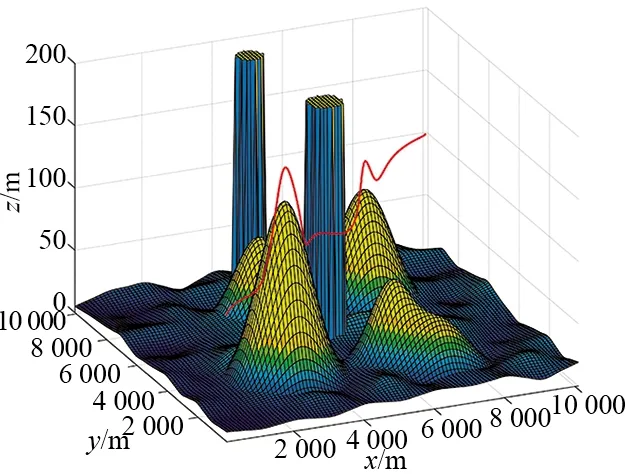
(c) IFFO最优航路

(d) PSO最优航路

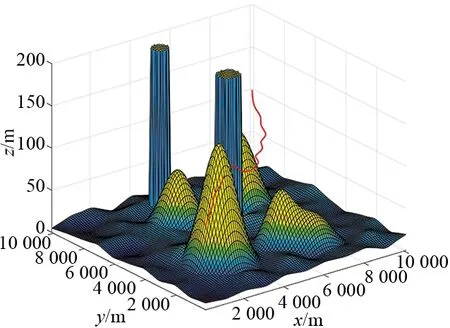
(e) DE最优航路

表3 最优航路数据结论

表4展示了5种算法分别独立运行50次的统计结果，分别展示了航路代价的最优值、中位数、平均值、最差值和标准差值，每一项的最佳值用粗体突出。

一般来说，生物启发算法的搜索能力和稳定性可以通过平均代价成本和标准差来反映。对比统计结果发现，改进FOA代价的最优值、中位数、平均值和最差值在5种算法中都是最小的，这表明改进FOA具有强大的寻优性能。虽然DE在5种算法中拥有最小的标准差，但是由图5和图7(e)可以看出，DE算法规划的航迹穿越了障碍物，该算法并没有找到安全可行的航路。因此，在所有能得到安全航路的算法中，改进FOA也拥有最小的标准差值，这进一步证明了改进FOA的高鲁棒性。总之，在有效性和鲁棒性方面，改进FOA的性能明显优于其他4种算法。

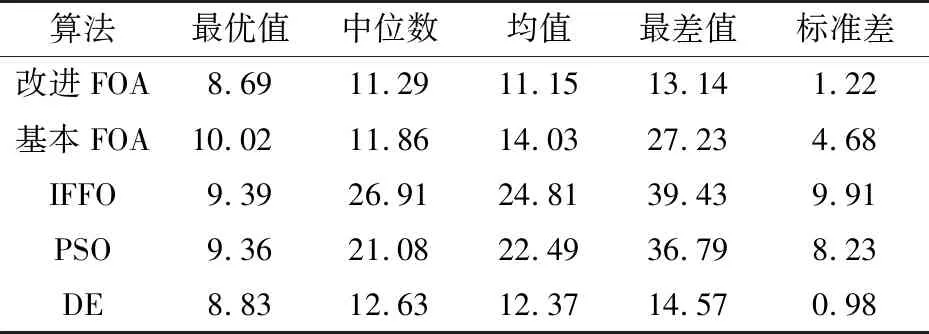
表4 算法性能比较

5 结论

将FOA应用于无人机静态航路规划中，并提出了FOA的改进版本。本文提出的改进FOA，从果蝇群位置的初始化、搜索步长以及跳出局部最优三方面对FOA进行了改进，成功解决了复杂地形和威胁环境下无人机静态航路规划问题。所提出混沌初始化策略增强了FOA在搜索能力方面的性能，自适应步长策略有助于FOA在收敛过程中实现高性能，模拟退火策略避免了FOA容易陷入局部最优的问题，本文给出的仿真实例说明了改进后FOA在无人机静态航路规划应用中具有较强的鲁棒性和有效性。