K-means聚类算法的一种改进方法研究
曾如明,李云飞
(西华师范大学 数学与信息学院,四川 南充,637009)
聚类分析是处理多元数据分类问题、挖掘数据内在信息进行统计决策的常用方式,在生物医学、经济统计等领域也广泛使用[1-2]。常用的聚类分析方法包括基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法、基于模型的方法和基于模糊理论的聚类算法[3]。而K-means聚类因具有简单性及高效性,因而成为研究性最强的划分式聚类算法[4]。
但K-means算法的聚类划分结果在很大程度上取决于初始聚类中心的选择。为了解决这个问题,众多学者针对初始聚类中心的优化问题进行了研究。HUANG等[5]采用特征加权法选取初始聚类中心,综合考虑了每个属性数据对聚类结果的影响;JIANG等[6]首先在样本数据集中将离群点剔除后选取K-means聚类的初始聚类中心;ZHANG等[7]基于密度选取初始聚类中心的思想对其进行改进,研究结果表明,改进的K-means聚类算法具有更高的稳定性和准确性;YODER和PRIEBE[8]考虑到随机选取初始聚类中心造成的聚类效果差等原因,提出K-means++聚类算法。翟东海等[9]为了解决初始聚类中心距离太近的问题,将距离最远的2个样本作为2个初始聚类中心,选取到前两个初始聚类中心距离之积最大的样本点作为下一个初始聚类中心;马克勤等[10]将距离最远的2个样本点作为初始聚类中心,将剩余样本点与已知聚类中心距离最小值组成的集合中选取最大值所对应的样本作为下一个聚类中心;韩凌波[11]以每个样本为中心,将一定区域内所含样本点的个数来衡量样本的密度,选取密度较大的k个样本作为初始聚类中心;文献[12-14]基于密度最大且相互距离较远的样本选取初始聚类中心,但在计算样本密度时需要引入参数,参数的选取会严重影响聚类效果,且参数的设置缺乏客观性,需要先进知识或者经验;周本金等[15]选择最大化减少聚类误差平方和的数据作为第t+1个聚类中心,实验表明,采用该方法不仅得到较好的聚类结果,而且迭代时间有所降低。
针对初始聚类中心对聚类的影响,本文对其选取方式进行改进。首先,根据密度和误差平方和优化初始聚类中心,利用改进算法将UCI数据库中所选取的数据集进行聚类,然后,选取合适的聚类有效性指标,对比不同聚类算法下的聚类效果。
1 相关理论
1.1 传统K-means聚类算法
K-means聚类是常用的划分式聚类算法之一。通过选取1种相似性度量方式将样本进行划分,使得相同类别中的数据尽可能相似[16]。算法的基本思想为采用欧氏距离衡量样本间的距离,将距离相近的样本聚成同一类,距离较远的样本聚成不同的类簇,直至得到初始划分的k个样本的集合。将每个类簇样本的均值作为下一次聚类的中心,计算剩余样本到新的聚类中心的距离并将其归类[17]。反复迭代,直至聚类准则函数收敛或者达到迭代次数为止[18-19]。
将w={x1,x2,…,xn}划分为k个类簇:w1,w2,… ,wn,其中,xi=(xi1,xi2,…,xim)Τ,c1,c2,…,ck为k个初始聚类中心,聚类过程中用到的定义如下[20]。
定义1 样本xi与xj之间的欧式距离:
定义2 样本xi到所有样本距离的平均值:
定义3 样本xi的方差:
定义4 数据集样本的平均距离:
定义5 误差平方和:
1.2 聚类有效性指标
聚类有效性指标用于衡量某次聚类的划分效果。为了评估聚类结果的质量,许多新的聚类有效性指标也不断被提出,这些指标可以分为3类:内部有效性指标、外部有效性指标和相对有效性指标[21-22]。其中,内部有效性指标不利用任何参考模型,由本身的聚类结果得到,主要基于数据集的几何结构信息从紧致性、分离度、重叠度等方面对聚类划分进行评价。外部有效性指标是指在已知数据真实分类的情况下,将本身的聚类结果与其进行比较,从而得出本次聚类划分的准确率与纯度等系数。相对有效性评价指标通过调整参数达到特定的评价标准,从而选取最优的参数及聚类模式[23]。常用的相对有效性评价指标有RS,CS和SD等。
2 基于方差和误差平方和的改进K-means聚类算法
K-means聚类随机选取初始聚类中心,具有容易选取到孤立点和异常点,或者选取的初始聚类中心之间距离较小等缺点。
基于上述2种缺点,文献[12-14]提出了基于密度和距离的初始聚类中心选取算法。首先,将样本数据集中最为紧密的样本作为第1个初始聚类中心。然后,以样本间平均距离为半径,将处于区域内的样本从数据集中删除,在剩余样本中选取密度最大的样本作为第2个初始聚类中心,仍然以样本间平均距离为半径,将区域内所在样本从数据集中删除,寻找下一个初始聚类中心,直至找到k个初始聚类中心。利用密度和距离优化算法,可以有效避免随机选取初始聚类中心而导致的聚类缺陷,从而提高聚类划分结果的质量。
2.1 基本原理
本文在基于密度和距离选取初始聚类中心的思想下,考虑到K-means算法本身是以最小化误差平方和为目标进行聚类,聚类的迭代过程,实际上就是误差平方和逐步减小的过程。为了在初始聚类中心选择阶段获取较小的误差平方和,本文以方差来衡量样本点的密度,根据最小方差选取中心,以样本间的平均距离为半径,选取k个位于不同区域且使该区域所有样本点的误差平方和最小的数据作为初始聚类中心。若k个初始聚类中心所在集合的误差平方和达到最小,则可以加快聚类的收敛速度,提高聚类质量。为了在聚类初始中心选择阶段获取较小的误差平方和,首先,计算所有样本的方差,选取方差最小的样本点为中心,以所有样本点的平均距离为半径,处于该区域的数据点构成集合w1;在剩余样本点中选取方差最小的样本点,并以所有样本点的平均距离为半径,将区域内所有样本点记为集合w2;直至找到k个位于不同区域且数据相对集中的集合;分别将集合w1,…,wk中所有样本点的均值作为k个初始聚类中心。由于k个集合是基于最小方差样本点(紧密度最高)为中心,所有样本间平均距离为半径进行划分并在k个集合中选取使得集合内误差平方和最小的数据作为k个初始聚类中心,故本文的优化K-means算法选取的初始聚类中心满足每个初始中心附近数据点尽量密集和k个初始聚类中心具有一定距离2个条件。
2.2 基本步骤
输入:n个m维样本的数据集,分类数目k。
输出:k个分类类簇。
1)选取初始聚类中心。
①根据定义1~3计算每个样本点的方差。
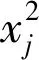
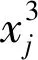
⑤直至找到k个较为紧密且互不干扰的样本集合w1,w2,…,wk。
⑥取w1,w2,…,wk每个集合的样本均值作为k个初始聚类中心。
2)构造初始划分。
①根据定义1计算所有样本点与k个初始聚类中心的欧式距离,并将其划分在最近的初始聚类中心所在的类中,即得初始划分集合。
②将初始划分得到的k个集合的均值作为中心,计算初始划分的误差平方和。
3)迭代更新。
①将上一次聚类划分得到的k个集合的均值作为本次的聚类中心,根据样本点与新的聚类中心之间的欧式距离重新构造划分。
②分别将所得k个类簇样本点的均值作为中心,计算划分的误差平方和。
③比较本次划分的误差平方和与上一次划分的误差平方和,若满足|EΤ-E|<10-10,即聚类中心不再变化,则迭代停止,输出最终的聚类划分结果。否则,继续运行,直至聚类中心不再发生变化为止。
3 实验结果与分析
为了测试本文所提算法的性能,分别采用传统K-means聚类算法、最大最小距离聚类算法、最小方差聚类算法和本文算法在UCI机器学习数据集(http://archive.ics.uci.edu/ml/index.php)上进行验证[24]。由于K-means聚类算法初始聚类中心选取的随机性和基于最大最小距离聚类算法的第1个初始聚类中心选取的随机性,为了验证算法的有效性,取100次聚类结果的平均值作为2种算法最后的聚类结果。本文采用外部有效性指标准确率、迭代时间和聚类误差平方和作为聚类评价指标。实验所采用的数据为UCI机器学习数据集中经常用来衡量聚类算法性能的数据集。选用的数据及其描述见表1。

表1 UCI数据集Table 1 UCI dataset
3.1 聚类误差平方和比较
本文算法在不需要任何参数调整条件下,在iris,wine和soybean-small 3个数据集上相对于传统K-means算法、最大最小距离算法有最小的误差平方和,聚类效果有很大提升,且本文算法与最小方差聚类算法在3个数据集上具有相同的误差平方和,即2种方法聚类效果一致,见表2。

表2 各算法的聚类误差平方和Table 2 The sum of squared of clustering errors of each algorithm
3.2 迭代次数比较
本文算法无论在iris、wine还是soybean-small数据集均有最小的迭代次数。原因在于,本文算法在基于密度和距离选取初始聚类中心的基础上,考虑了聚类的原则,使最终划分结果中处于同一类中的样本数据尽可能地相似,故在初始聚类中心选择阶段从相互独立且样本较为密集的k个集合中选出使得各个集合内误差平方和最小的k个数据。由于聚类的每一次迭代过程就是使聚类误差平方和逐渐减小的过程,故在初始聚类中心选择阶段,使k个区域的误差平方和最小将会减少后续的迭代次数,从而使得本文算法所需要的迭代次数比其他算法明显减少,收敛速度加快,见表3。

表3 各算法的迭代次数Table 3 Iteration times of each algorithm
3.3 准确率比较
各算法对iris,wine和soybean-small 3个数据集聚类划分的准确率见表4。由表4可以看出本文算法在3个数据集上的准确率相对于传统K-means算法、最大最小距离算法来说都是最高的,本文算法和最小方差算法在3个数据集上的聚类准确率相同;对于iris和soybean-small数据集来说,其他算法的准确率均高于传统K-means算法,但wine数据集的最大最小距离的聚类准确率低于传统K-means聚类准确率,这可能是因为该算法在选取初始聚类中心时,随机选取1个样本点作为第1个聚类中心,然后根据最大距离原则选取下一个聚类中心,并没有考虑选取离群点作为初始聚类中心对聚类结果产生的影响。

表4 各算法准确率 Table 4 Accuracy of each algorithm %
综上所述,本文算法较传统K-means聚类算法、最大最小距离算法相比在误差平方和、迭代次数及准确率这3个聚类评价指标上都有较大提升。与最小方差聚类算法相比,最终聚类结果具有相同的准确率及误差平方和,但在聚类过程中需要更少的迭代次数,收敛速度更快。原因在于本文是在最小方差聚类算法选取初始聚类中心的基础上,考虑了误差平方和在聚类中的作用,通过最小化初始聚类中心所在区域的聚类误差平方和,减少了聚类的迭代次数,加快了收敛速度。
4 结论
针对传统K-means聚类算法随机选取初始聚类中心带来的聚类稳定性差及聚类质量低以及现有优化初始聚类中心的K-means算法需依赖一些参数,参数的设置缺乏客观性,聚类结果取决于参数选取质量等缺点,提出了1种结合方差和误差平方和的改进K-means聚类算法。算法首先基于方差和距离选取出k个位于不同区域,且样本点相对集中的集合,然后根据最小化误差平方和的思想,选取使k个所选集合的误差平方和最小的数据作为k个初始聚类中心。利用本文算法与其他算法对iris,wine与soybean-small数据集进行聚类划分,结果表明,改进算法能够加快聚类的收敛速度,且聚类效果更好。

