UHPC华夫桥面单向板的荷载有效分布宽度及抗弯承载力计算方法

朱劲松 王修策 丁婧楠 陈胜利

(1天津大学建筑工程学院, 天津 300072)(2天津大学滨海土木工程结构与安全教育部重点实验室, 天津 300072)

连续组合梁桥中主梁或横隔梁间的普通混凝土桥面板在车辆荷载作用下会产生拉应力而易开裂,影响桥面板的耐久性.UHPC作为一种集超高强度、超高韧性、超高耐久性于一体的新型水泥基复合材料可用于建造桥面板,以改善其开裂问题.由于UHPC的强度远高于普通混凝土,故在相同荷载条件下UHPC桥面板厚度远小于普通混凝土板,从而导致桥面板截面刚度降低.采用UHPC华夫板作为桥面板则既可发挥UHPC优异的力学性能,又可保证桥面板的截面刚度.国内外学者已经验证了UHPC华夫板作为桥面板的可行性[1-2],对UHPC华夫桥面板的结构性能进行了评估[3],并建议在计算UHPC华夫板抗弯承载力时将沿桥梁横向简化为一系列T形梁[4].桥面板在车轮荷载作用下,除直接承压部分的板带外,与其相邻的板带也会参与工作,因此需确定其荷载有效分布宽度.目前的梁桥设计中,桥面板多属单向板,现行各国规范中单向桥面板荷载有效分布宽度主要与桥面板横向跨度呈一定的比例关系.国内学者已对交叉梁体系桥面板[5]与波形钢腹板箱梁桥面板[6]的荷载有效分布宽度进行了相关研究,但关于UHPC华夫桥面板荷载有效分布宽度计算方法的相关研究则较为少见.

本文采用ANSYS软件建立了华夫桥面单向板参数化模型,分析其荷载有效分布宽度,拟合出考虑华夫板横向跨径和横肋间距的荷载有效分布宽度经验公式,提出了UHPC华夫桥面单向板抗弯承载力和有效分布宽度的计算方法.将计算结果与试验结果进行对比,以验证所提方法的可靠性和适用性.

1 荷载有效分布宽度

(1)

(a) 华夫桥面板结构

(b) 车轮荷载

(c) 荷载有效分布宽度

2 有限元分析

通过有限元软件ANSYS对文献[2,4,7]中的试验进行模拟,3组试件分别为UHPC简支矩形梁B2[7]、UHPC简支T形梁T3[4]和单跨固支华夫板Test7[2],模型尺寸及材料性能参数均按文献取值.有限元模型中采用solid65单元模拟UHPC,采用link10单元模拟钢筋,采用精度较高的映射网格划分方法进行网格划分.

有限元模型中UHPC和钢筋本构关系均采用双折线简化模型.UHPC本构关系如图2(a)所示.图中,σ为应力；ε为应变；fc为轴心抗压强度；ft为抗拉强度；Ec为UHPC的弹性模量；峰值压应变εc0=fc/Ec；极限压应变εcu=εc0+0.001[8],峰值拉应变εt0=ft/Ec；极限拉应变εtu=30ft/Ec[8].钢筋本构关系如图2(b)所示.图中,fy为屈服抗拉强度；εsy为屈服应变；fu为极限抗拉强度；εsu为极限应变；Es为钢筋的弹性模量；塑性强化模量ET=0.01Es.

(a) UHPC

图3为数值模拟与试验实测的荷载-位移曲线.由图可见,试件B2与Test7的弹性阶段刚度吻合良好,试件T3的弹性阶段刚度模拟值略高于试验值.试件B2、T3与Test7的极限承载力模拟值与试验值基本一致.可见该有限元模型可以较好地模拟UHPC梁和华夫板的破坏过程.

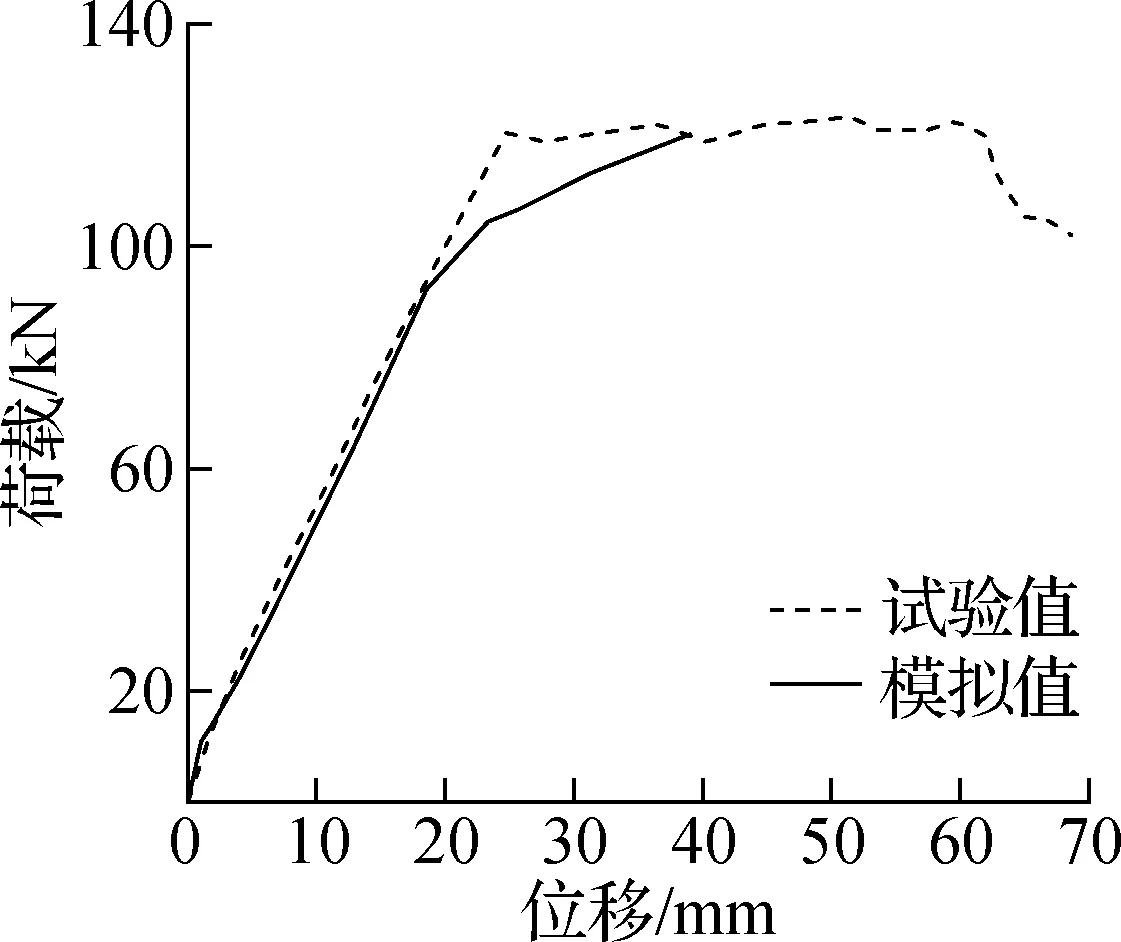
(a) 试件B2

(b) 试件T3

(c) 试件Test7

图4为各试件数值模拟的等效应力云图.由图可见,试件B2与Test7破坏时UHPC的等效应力接近轴心抗压强度,试件T3的等效应力最大值为55.4 MPa,约为轴心抗压强度的1/2,这是因为试件T3的受拉钢筋配筋率低,受拉钢筋过早屈服,导致少筋梁破坏.

(a) 试件B2

(b) 试件T3

(c) 试件Test7

3 荷载有效分布宽度

采用第2节中的ANSYS建模方法建立华夫桥面单向板有限元模型,且UHPC和钢筋的本构关系均采用简化的双折线模型.UHPC的轴心抗压强度取150 MPa,抗拉强度取7.5 MPa,弹性模量采用文献[9]中的拟合公式进行计算取值.由于UHPC的抗压强度高,并且掺入大量钢纤维,故模型中未配置受压钢筋和箍筋,仅在肋板受拉区配置1根直径为22 mm的HRB400钢筋.

华夫桥面板结构如图1所示.本文共建立了41组华夫桥面单向板有限元模型并进行参数化分析,具体参数如下：L=1 500～3 500 mm；St=250～750 mm；Sl=300～1 300 mm；ts=40～80 mm；hr=100～140 mm；br=80～120 mm；a1=200～1 000 mm；b1=300～900 mm；边界条件分为简支和固支；受力阶段分为弹性和塑性阶段.考虑华夫桥面板最不利受力情况及受力特点,取面荷载作用于华夫桥面板中心位置,且该处仅布置横肋而不布置纵肋(见图1).标准模型参数取L=2 500 mm；St=500 mm；Sl=800 mm；ts=60 mm；hr=120 mm；br=100 mm；荷载形式根据《公路桥涵设计通用规范》[10]取中后车轮荷载,着地面积a1b1=200 mm×600 mm.

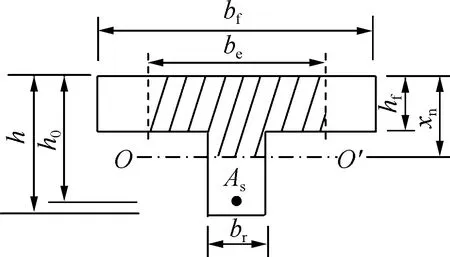
华夫桥面板横向跨径、纵横肋尺寸与布置、荷载作用面积及支承条件等因素在弹性阶段和塑性阶段对华夫桥面单向板有效分布宽度的影响规律如图5所示.由于固支板相比简支板应力分布更为均匀,两边固支的华夫板有效分布宽度要比简支板小30%～50%.简支板在弹性阶段荷载有效分布宽度小于塑性阶段,而固支板弹性阶段荷载有效分布宽度大于塑性阶段.这是因为简支板属于静定结构,塑性应力重分布使得应力趋于均匀且不会引起内力重分布,而固支板属于超静定结构,其塑性应力重分布会引起内力重分布.由图5可见,华夫板荷载有效分布宽度随华夫板横向跨径和横肋间距的增大而增大,随肋高和肋宽变化不明显.简支华夫板荷载有效分布宽度随面板厚度增大略有增大,而面固支华夫板荷载有效分布宽度则不受板厚度变化影响.当b1St-br时,则随纵肋间距增大明显减小.当a1Sl-br时,则随荷载纵向宽度增大而明显增大.由此可知,当华夫桥面板纵横肋间距和车轮荷载面积满足a1

(a) 随横向跨径变化

(c) 随肋宽变化

(f) 随纵肋间距变化

基于数值分析结果,采用MATLAB拟合工具箱CFTOOL中的多项式,拟合得到UHPC华夫桥面单向板荷载有效分布宽度a与华夫桥面板横向跨度L及横肋间距St的关系如下：

(2)

在固支弹性阶段,基于文献[11-12]及式(2)得到的华夫桥面单向板荷载有效分布宽度随桥面板横向跨径变化趋势见图6.由图可见,St=0.8L且L<2 000 mm时,式(2)计算值接近文献[12]结果；St=0.8L且L>2 000 mm时,式(2)计算值明显大于文献[11-12]结果；St=0.6L时,式(2)计算值介于文献[11-12]结果之间；St=0.4L且L>2 000 mm时,式(2)计算值明显小于文献[11-12]结果；St=0.4L且L<2 000 mm时,式(2)结果接近文献[11]结果；St=0.2L时,式(2)计算值明显小于文献[11]结果.因此,当华夫桥面板的横向跨径、肋宽、纵横肋间距及车轮荷载宽度满足a1

图6 式(2)计算值与文献[11-12]结果对比

4 抗弯承载力计算

如图1所示,可将华夫桥面板简化为一系列的T梁,华夫板的整体抗弯承载力即为荷载有效分布宽度a内T梁的承载力之和.图7为T梁抗弯承载力计算示意图.图中,h为T梁高度；h0为钢筋至T梁上边缘的距离；hf为翼板厚度；bf为翼板宽度；be为翼缘有效宽度；As为钢筋截面积；xn为受压区高度；xte为弹性受拉区高度；xte为塑性受拉区高度；εc为受压区上边缘UHPC压应变；εs为钢筋拉应变；σc为受压区上边缘UHPC应力；σs为钢筋应力.

(a) T梁横截面图

(b) 开裂状态时截面应力与应变分布

(c) 极限状态时截面应变与应力分布

4.1 开裂承载力

T梁下边缘UHPC拉应力达到抗拉强度时认为梁底开裂.此时的应力应变分布如图7(b)所示.可根据几何关系计算εc与εs,则σc=Ecεc,σs=Esεs,进而得到受压合力C和受拉合力T分别为

(3)

(4)

令C=T,确定xn及xte,对中性轴取矩得到T梁开裂弯矩为

(5)

则华夫桥面板整体开裂弯矩的计算公式为

(6)

4.2 极限承载力

由于UHPC的抗压强度高,在实际工程中其抗压强度很难充分利用,因此UHPC华夫板的极限破坏由受拉钢筋屈服控制.当T梁达到承载力极限状态时,截面应力、应变分布如图7(c)所示.钢筋应变εsy=fy/Es,根据几何关系可计算得到受压区上边缘UHPC压应变εc,则受压区上边缘UHPC应力σc=Ecεc,此时受压合力C的表达式与式(3)相同,受拉合力T为

(7)

令C=T,确定xn、xte和xtp,对中性轴取矩得到T梁极限弯矩为

(8)

则华夫桥面板整体极限弯矩的计算公式为

(9)

文献[2,4,7]中的试验结果与本文抗弯承载力公式计算结果比较见表1和表2.表中,Mcrt、Mut分别为开裂弯矩和极限弯矩的试验值；Mcra、McrCa、McrAa分别为基于式(2)、文献[11-12]的荷载有效分布宽度通过式(6)得到的开裂弯矩计算值；Mua、MuCa和MuAa分别为基于式(2)、文献[11-12]的荷载有效分布宽度通过式(9)得到的极限弯矩计算值.由表可知,McrCa、McrAa与Mcrt的误差较大,而Mcra则与Mcrt基本一致.与Mua相比,MuCa与Mut更为接近,但较MuCa与MuAa更为保守,且各试件中Mua与Mut的最大误差在20%以内.由此说明,本文所提出的有效分布宽度法更为合理.

表1 开裂弯矩的试验值与计算值对比 kN·m

表2 极限弯矩的试验值与计算值对比 kN·m

5 结论

1) ANSYS有限元分析结果与文献中的UHPC矩形梁、矮肋T梁和华夫板抗弯承载力试验结果吻合较好,从而验证了UHPC和钢筋采用简化双折线本构关系的有限元模拟的可靠性.

2) 固支华夫桥面单向板的荷载有效分布宽度较简支板小30%～50%.当华夫桥面板的纵横肋间距和车轮荷载宽度满足a1

3) 在华夫桥面板的横向跨径、肋宽、纵横肋间距及车轮荷载面积满足a1

4) 基于平截面假定推导了华夫桥面单向板抗弯承载力和有效分布宽度计算方法,由其得到的计算结果与试验结果吻合较好,从而验证了该方法的可靠性与适用性.