高频驱动条件下法拉第斑图生成的临界参数探究

严 涵，王 伟，周路群

(北京大学 物理学院，北京 100871 )

竖直方向的周期性驱动力作用于液体，可使其表面产生有序的周期性结构——这一现象最早被法拉第研究[1]，称为“法拉第斑图”.

理论上，为定量研究这一现象，需要在流体动力学的纳维-斯托克斯(Navier-Stokes)方程中加入表面张力和黏滞阻力的贡献项.20世纪中叶，Benjamin和Ursell分析了不含黏滞阻力项的情形，得到了振幅随时间演化的方程，并表述为Mathieu方程的标准形式.由此，他们定量地预言了依赖于外界的驱动振幅和驱动频率的法拉第斑图的生成条件[2].其生成机制为溶液系统在特定边界条件下的本征模式与外界驱动参数作用下达到参数共振，这一理论框架在低频条件下被较充分地进行了实验检验(根据实验观察经验及前人研究[3]，在本实验条件下，“低频”即可用线性理论近似描述的区域大致在40 Hz以下，高频大致在60 Hz以上)，并得到了理论和实验上的推广[4].然而，在较高的驱动频率下，非线性效应更为显著，前述理论的预言能力较为有限.实验观察表明，在高频驱动条件下，法拉第斑图生成的参数条件受溶液系统边界条件的影响较小，其生成和选择问题极大地依赖溶液本身的特性.

本实验关注高频驱动条件下黄原胶溶液生成法拉第斑图的临界参数关系，发现最大驱动加速度Acc与驱动频率f存在准线性变化关系，这个线性关系预示着驱动加速度和驱动频率的比值存在常量的可能，即某种速率特征量可能是描述法拉第斑图生成行为的特征量.之后，本文尝试使用修改后的纳维-斯托克斯方程，得到基于溶液系统能量耗散和外界能量输入达到平衡的有关临界参数的半定量理论关系预言.然后，根据实验结果和理论预言的对比，提出液面速率可能是描述系统斑图生成行为的特征量，并指出了进行进一步研究的可能.

1 仪器及测量方案介绍

1.1 实验仪器介绍

实验仪器由模态激振器(JZK-100)、扫频信号发生器(YE1311)、功率放大器(YE5878)、压电式加速度传感器(GA-YD-107)、电荷放大器(YE5852)(这五部分购自江苏联能电子技术有限公司)以及示波器(TDS1002，泰克科技中国有限公司)和高速摄像机(AOS S-MOTION，瑞士AOS公司，AOS Technologies AG)组成.扫频信号发生器输出特定频率f、特定振幅Am的交变信号，经功率放大器放大后，输入模态激振器，使固连于其上的平板以及无盖圆形容器在竖直方向上周期性振动.固定在平板上的加速度传感器将加速度信号经电荷放大器输入示波器，通过读出示波器电压峰-峰值(记为U)可知平台振动的最大驱动加速度值Acc∝U(比例系数受电荷放大器控制，为一常数，单位ms-2V-1).在实验过程中，可使用安装在圆形容器上方的高速摄像机观察液体表面的图样.实验装置示意图如图1所示，该图参考自同一实验平台进行实验的亓瑞时等人的论文[3].

图1 实验装置示意图

本实验中，溶液系统为具有一定黏稠性的黄原胶溶液.黄原胶溶液是有黏性的非理想流体，应用于法拉第斑图的研究，能获得更丰富稳定的非线性物理效应.另外，本实验希望关注黄原胶溶液的表面性质，希望尽可能减少系统整体几何属性如容器边界、液体深度的影响.之前低频段的研究表明：液体深度较大(远大于重力波波长)时，深度对液面结构的影响近似可以忽略；而高频段的定性实验则表明，容器口径较大时边界的影响较小.因此，本文选用较大口径(直径D=14 cm)的圆形容器，分别加入150 ml、250 ml溶液(深度分别为0.97 cm、1.62 cm)进行实验.根据预实验，选取斑图易于产生、便于观察的典型浓度c=5 mg/ml进行实验.

1.2 实验现象及测量方案

固定信号发生器输出频率，即固定驱动频率f，缓慢调大输出信号幅值U，可以观测到在某一特定参数范围内，溶液表面迅速“生长”出一定的有序结构，即法拉第斑图.在低频时，这种结构一般分布于整个液面或其中某个对称轴上，并展现出显著的对称性[4]；高频时，这种结构更倾向于表现出“晶格”的状态，同时其开始出现的区域也不必然对称地分布于整个液面上，而是呈现出更多样的状态.图2给出了几个例子.

(a) f=60 Hz时的“半环”结构 (b) f=90 Hz时的“半环+半带”结构

待斑图稳定后，缓慢调低U，斑图将消失.其对应的U不必然等于前述增大U时的“临界值”，即展现出某种“滞回”现象.一般而言，当频率较高时，上下两个临界值分辨得较为清楚，且增大时的临界值(记为U1)一般高于降低时的临界值(记为U2).

考虑到仪器的精度和稳定性，驱动频率选取信号发生器的输出值，驱动外力选取示波器上由加速度传感器测得的加速度峰-峰值(用电压表示，如前所述).为尽可能提高实验结果的可重复性，本实验在操作时要求尽可能按照示波器可观测的最小分辨率来调节信号发生器输出，每调节到一个输出值，等待5 s并利用高速摄像机传回的画面观察斑图是否出现.

需要特别说明的是，“斑图是否出现”的判定是依据肉眼对频幕上高速摄像机传回图像的观察.这种判据之所以有一定的可重复性，是因为斑图出现时液体表面驻波振幅是“跳变”(迅速增长到可观察的水平)而非缓慢增大的.当然，这种判据的引入，使得其结果必然带有一定的主观性，存在一定的系统误差.

2 实验结果

选用浓度固定为5 mg/ml的黄原胶溶液，分别测量溶液体积为Va=150 ml和Vb=250 ml时的上下两个临界电压U1和U2.频率以5 Hz为间隔变化，实验结果如图3所示.

(a) Va=150 ml

从图3中可以看出，临界电压近似线性正相关地依赖于驱动频率.需要说明的是，两图中曲线在65 Hz附近的明显“凹陷”可以被解释为仪器平台的共振效应——在这频率附近可观察到整个激振器有较大的、宏观可见的晃动，且在同一平台上进行实验的其他研究者也报告了相似的现象.由此，本文将65 Hz处的数据的“偏移”视为外界干扰导致，在之后拟合分析时舍去该点.为更准确地研究临界电压对驱动频率的依赖关系，对二者均取对数，再进行分析.考虑到中频(小于60 Hz)上下两个临界点可能有“倒转”现象(即不符合通常所见的U1>U2情形)、且不能很好的排除在误差范围之外，本文参考之前研究者的做法[3]，对同一频率的上下两值取平均后再取对数，进行进一步分析.计算结果表明这一做法对后续的幂指数分析几乎没有影响.

图4即为按上述方案进行处理的结果.图中的两条直线是对数取平均后的数据进行线性拟合生成的(已舍去65 Hz的点.实际上这一操作对拟合结果影响很小).线性拟合的参数如表1所示，其中σa、σb为拟合直线参数的不确定度(未考虑单次测量误差).

令人感兴趣的现象是图4的线性拟合结果，因临界电压U正比于溶液系统的最大驱动加速度Acc，故有lnAcc∝lnf，而表1显示二者线性拟合的斜率接近1，这预示着驱动加速度和驱动频率的比值存在是常量的可能，即某种速率特征量可能是描述法拉第斑图生成行为的特征量.若斜率严格等于1，这个速率特征量就是外界驱动溶液系统即平台的最大速率，也就是说，当外界周期驱动力足够大，使得平台带动溶液系统在上下振动过程中其最大瞬时速率达到某个临界值，斑图就会生成，概括地说就是斑图是否生成取决于溶液系统所处平台的最大速率是否越过这个临界值.

图4 临界点随频率变化的线性拟合结果

表1 临界点随频率变化关系的线性拟合(lnU=a*lnf+b)结果

接下来，继续关心拟合直线的斜率偏离1的程度，因为这反映了Acc对f的依赖关系偏离线性的程度.从实验结果来看，拟合得到的斜率大致在1.2～1.3的范围内，有系统性的对1的偏离——不妨把这种关系称作“准线性”关系.这种偏离表明本文的猜想“平台最大速率存在控制斑图生成的临界值”不太准确.在下一节中，将尝试对此给出一个半定量的理论解释，并讨论其可能的物理意义.

3 半定量理论分析与讨论

从考虑表面张力的理想流体的纳维-斯托克斯方程出发，方程的原始版本一般为关于速度势的形式[2,5]：

(1)

式中z坐标指向竖直方向(以竖直向上为正)，ζ为液体表面的z坐标，仅为x、y、t的函数；g为(z方向的)重力加速度.该式假设了小振幅运动的理想流体(不可压缩、不考虑粘滞).对其求梯度，并进行推广——补充黏滞项、推广加速度项，得到

(2)

式中最后补充的一项黏滞项为仿照教材[5]中常见写法给出的形式；g*为推广的、可依赖于时间变化的“重力加速度”.对于本实验所涉及的情况，可以写出

g*=g+Acccos(2πft+φ)

(3)

式中g、Acc均为常矢量.式(2)两边点乘v，再对起振的空间区域取平均，得到

(4)

对式(4)的导出，有几个说明：首先，最后一项尖括号中并矢的定义为v:v=(∂kvi)(∂kvi)(重复指标需求和)；其二，式(2)中右边第二项的空间积分可利用散度定理化为区域边界处结果为零的积分(注意不可压缩流体即速度场无散的假设)；其三，式(2)中最后一项利用分部积分的办法，可得到式(4)中的最后一项.

在式(2)成立的情况下，式(4)是严格的.然而，为与本文的实验尽可能相对照，需再做一定假设的基础上简化式(4).本文对式(4)进行时间上的平均.这样，左边就可理解为某种“平均起振幅度”随时间的变化.令其为0后，还需要得到等式右边的简化结果.将各振动量的幅值用下角标m表示，得到如下近似表达式

(5)

其中，k为表面张力重力波的波数，注意到无黏滞条件下重力波速度场的解析结果在各空间方向上都有对k的依赖(参见教材[5]相关内容).在能量角度下，这等式可近似的理解为斑图生成临界点处的能量平衡方程，即外“重力场”的做功与起振流体黏滞耗散的能量相平衡.考虑到高频、较大深度条件下，如下的色散关系符合得较好

(6)

由此，式(5)化为

(7)

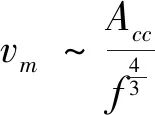
最后，实验结果的幂指数在1.2～1.3的范围内，离理论分析的结果4/3还有一定的差距.这极有可能源自黄原胶溶液是非牛顿黏性流体的特性，以及判断斑图生成的临界状态的主观性等方面带来的误差.

将来，进一步的研究可以在实验层面尝试证实或证伪这一推论，也可以在理论角度考察这一结果的物理意义——例如，这是否包含了一类非线性系统的普遍特性，或者反映了某种类似标度律的属性.

4 结束语

本实验观察高频周期外力驱动的黄原胶溶液表面生成法拉第斑图的临界参数的情形，得到了临界参数最大驱动加速度对驱动频率的准线性指数依赖关系，其幂指数约为1.2～1.3.基于一种半定量的理论分析，本文得到了一个类似于能量平衡方程的关系式，且相应的理论幂指数为4/3.由此推断，在斑图生成的临界状态附近，溶液表面最大速率可能存在临界值，也就是说，当外界驱动溶液时，溶液表面在上下振动时其最大速率若达到这个临界值，斑图就可能瞬间生成；同时也猜测，溶液表面最大速率可能是体系一重要的特征量.

5 致谢

本实验得以完成，需要感谢北京大学物理学院的场地、仪器支持，周路群、王伟老师的指导、帮助，以及与赵瑞博同学的讨论交流.此外，本实验的有关想法也受到了诸多前辈包括在同一实验室进行过实验的学长们的启发，在此一并表示感谢.