考虑机组分类的海上风电短期功率预测-校正模型

祁 乐，唐 健，江 平，郑芳雯，刘德志

（1.广西电网电力调度控制中心，广西 南宁 530023；2.北京心知科技有限公司，北京 100102）

0 引言

随着海上风电制造、安装、并网成本的逐步下降，海上风电开发不断向深海拓展，预计中国海上风电累计装机容量将在2025年达到2 500万kW［1］。海上风电场装机规模大、风能质量高，但因海上存在风流热效应和放大的尾流效应等，且海上风电功率预测技术发展较晚，故海上风电功率预测一般以陆上风电模型为基准，并结合海上特征加以改进，相关研究证明该做法切实可行［2］。

传统的风功率预测方法可分为物理模型、统计模型和将二者结合的方法［3］。随着气象数值模式性能的提高，目前主流采用结合法，即使用机器学习方法对数值天气预报（Numerical Weather Prediction，NWP）风速预测结果进行误差订正后处理，得到较为准确的风速，并基于优化后的风速进行风电功率预测［4］。

通过引入多位置NWP 信息，可有效避免出现单位置NWP 无法准确描述风电场气象信息的问题，提高预测精度［5-6］。文献［7］同时考虑多位置NWP 与非典型气象特征，基于最大相关-最小冗余原则和主成分分析进行特征选择，减少整体冗余性，有效降低了预测模型的训练时间。此外，考虑风机数据的时间相关性，用聚类分析方法生成不同天气类型数据，针对不同天气类型进行NWP 数据订正后处理，能进一步提升预报能力［8］。文献［9］考虑功率变化趋势，获取更优的性能，可在一定程度上解决功率波动大的问题，即爬坡问题。然而上述研究只针对风电场的单一风速，缺乏对大型风电场内部差异的充分考虑，没有利用机组各风机的历史信息。

机组分类是研究大型风电场发电规律的重要手段，相关研究也表明基于风电场机组分类的功率输出模型能有效代表实际功率输出情况，可降低功率建模过程的复杂度和时间［10］。近年来，考虑机组分类的短期功率预测的研究表明，风电场内不同风机受地形、尾流、湍流影响而差异明显，基于机组分类的功率预测优于单一风速的功率预测［11-13］。但遗憾的是，此类研究均仅简单对机组的所有子类进行功率预测建模，并采用叠加法对将预测功率累加求和，受到各个子类预测精度的影响，模型误差累计造成其精度偏低。

综上所述，提出一种考虑多NWP 和机组分类的功率预测校正模型，基于多NWP 信息和单一风速进行风速订正后处理，并通过理想功率曲线，生成初始预测功率。然后基于层次聚类［14］，将风电场内风力发电机组分类成若干代表组，生成若干组预测风速；通过正则化极限学习机（Regularized Extreme Learning Machine，RELM）建立代表预报风速与初始预测功率残差的关系，最终校正初始预测功率。通过算例分析，所提出的模型能有机结合多NWP 和机组内部信息，有效避免极端误报，提高考核天的准确率，减少短期功率预测考核电量。

1 海上风电功率预测的校正模型结构

建立的海上风电功率模型主要由初步预测功率模型和考虑机组分类的校正模型两部分组成。

初步预测功率模型采用经典的两步法，首先使用物理模型和统计模型结合的方法预测风速，为了考虑多位置的NWP信息，采用适合处理高维样本的极限梯度提升树（Extreme Gradient Boosting，XGBoost）模型作为统计学模型，然后将订正后的NWP 预测风速代入理想功率曲线（曲线由风机信息所得），得到初始预测功率。

为引入风场内部差异信息，基于层次聚类将机组S 台风机风速分类为G 组，生成G 组子类平均风速，经订正后处理模块生成G 组预测风速，作为RELM 模型的输入，模拟初始预测功率与实际观测功率的差值，最终校正初始预测功率。

如图1所示，设置3组实验。

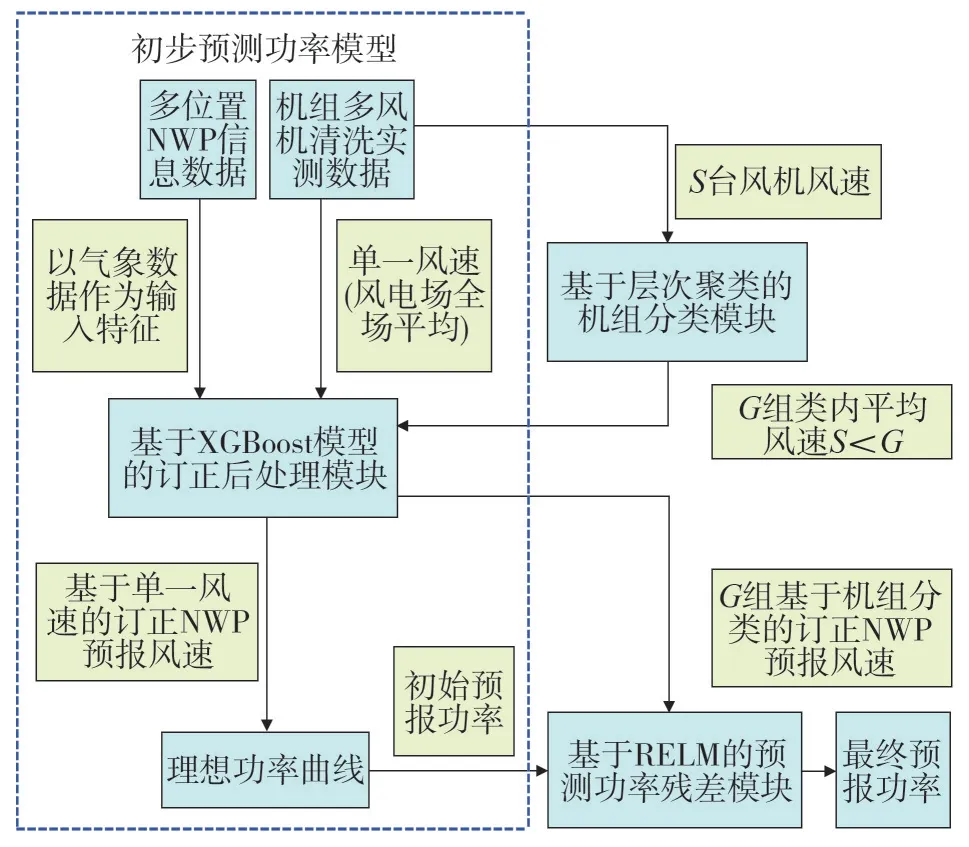
图1 风功率预测流程

1）单一风速：将风电场平均风速作为优化目标，经XGBoost 模型得优化预报风速，代入理想功率曲线，得预测功率P1。

2）机组分类：基于层次聚类，将S 台风机分为G组，分别以G 组平均风速作为优化目标，得G 组优化预报风速W，代入理想功率曲线得各组预测功率，累加得风电场预测功率P2。

3）RELM 校正：设预测功率P1与真实功率的差距为残差D，以D 为优化目标，W 为RELM 模型输入，预测残差与P1之和即为最终预测功率P3。

2 初始预测模型的建立

2.1 多NWP的特征选择

为覆盖风电场更大范围、涵盖各种地形，应选取风电场周边典型4～9 个位置的NWP 的气象数据，每个位置包含4 个高度层的经向风、纬向风、温度、湿度、气压等5 个参数信息，即每个时刻最多含180 维数据。NWP 为未来72 h 预报数据，每天进行一次更新，时间分辨率插值至15 min。

2.2 基于层次聚类的机组分类

对机组分类时，层次聚类法无须先验地指定子类的个数。相较k 点均值中心法kmeans、模糊C 点均值中心法（Fuzzy C Means，FCM）等方法，可添加约束，调整子类的个数。基于此，采用层次聚类法中的凝聚法，采用自底向上策略，输入数据机组内所有风机的相似性度量向量矩阵，逐步合并相似距离相近的风机为一类，直至将所有风机聚为一个大类。具体流程为：

1）设N 为样本数，M 为风机数，选取同一时间段参与并网的M1台风机，构建N×M1阶矩阵；

2）基于欧式距离、皮尔逊相关系数、熵相关系数，计算M1个风机两两间的相似性度量矩阵。

3）利用离差平方和法［15］计算不通类之间的距离d，每缩小一类，离差平方和SX就要增大，选择使SX增加最小的两类合并，如式（1）所示。

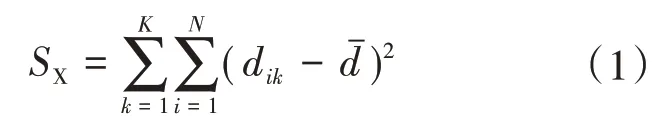
4）若类的个数不等于1，则重复执行步骤3），否则执行步骤5）。

5）保证类内的风机数不超过总风机数一半，取子类个数的最大值。

6）计算聚类评判标准指数［16］，确定计算相似性度量的方法。

设Y 为历史功率，X 为历史气象数据，则上述提及相似度距离公式为：

①欧式距离DXY为

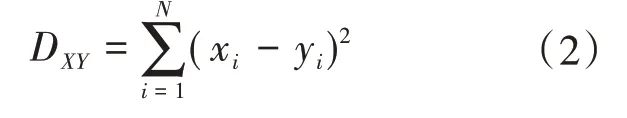
式中：xi、yi分别为样本i的气象数据和功率数据。

②皮尔逊相关系数ρXY为

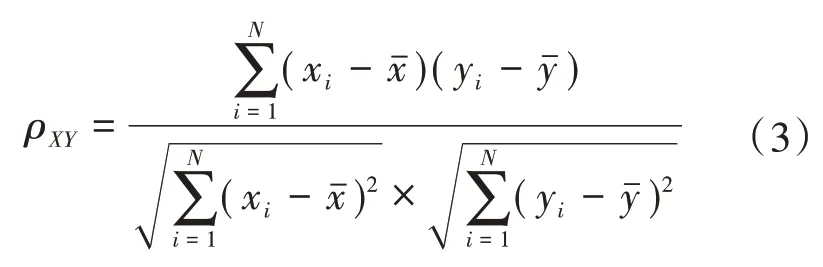
③熵相关系数IXY为

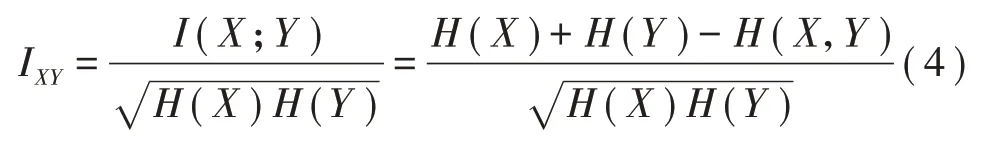
式中：H（X）为X 的信息熵；H（X，Y）为X、Y 联合熵；I（X；Y）为互信息，表示X 和Y 之间共享信息量的多少。信息熵和联合熵分别定义为：

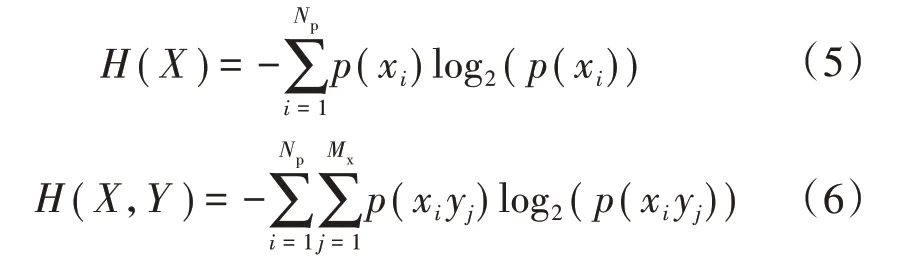
式中：p（·）为落入区间的频率；MX、Np分别为X、Y 升序排列等分的子区间的个数，对于等分区间个数可参考式（7）。

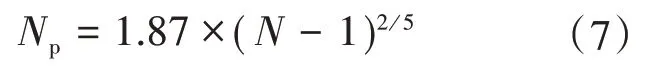
④另外，聚类评价标准选取基于标准差指数（Standard Deviation Based Index，STDI）ISTD，其定义为类间距离与类内距离之比，如式（8）所示，其值越大代表聚类效果越好。

式中：ck为第k类的质心；为所有样本的质心；xi为第k类中的第i个样本；nk为第k类中所有样本数。

2.3 XGBoost模型

NWP 作为输入特征，经XGBoost 模型后获得预测风速，而预测风速的准确性是预测功率是否准确的关键。XGBoost 为梯度提升树（Gradient Boosting，GBoost）算法的改良版本，Boosting 属于串行的集成方法，第t 个弱学习器优化学习前t-1 个学习器的残差部分，逐步引入学习器而最大化地降低目标函数，进而得到一个强学习器。由于多NWP 数据具有多维（180 个）特征，XGBoost 构建学习器时会对特征采样，并添加正则项，防止过拟合，同时训练速度快，十分适合NWP风速订正后处理［17］。

XGBoost 算法以CART 回归树为弱学习器，预测函数输出y′为

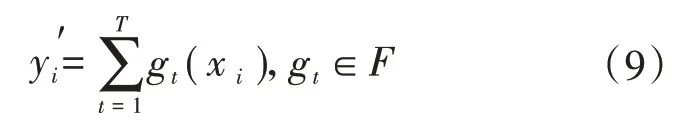
式中：gt（·）为CART回归树；xi为输入特征，i=1，…，N；T 为XGBoost 超参数，指共有T 个弱学习器；F 为搜索空间。

正则化目标函数为

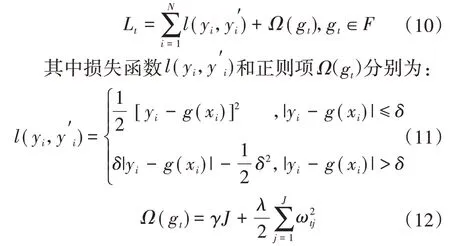
式中：yi为真值样本，i=1，…，N；J 为叶子节点的个数；ω为各叶子节点权重，δ、γ、λ为超参数。

则训练过程如下：

1）对所有样本，初始化一颗CART 树，同时得预测输出g0为

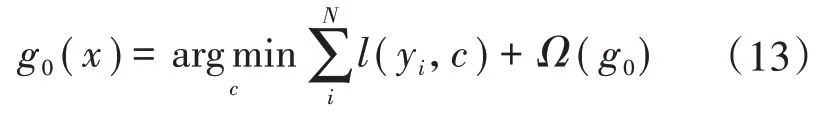
式中：c为预测输出集合

2）对所有样本计算负梯度rti为

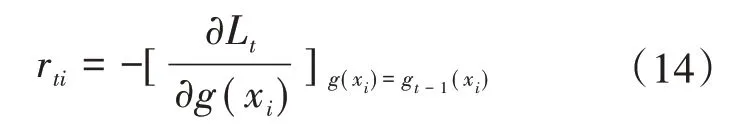
3）利用负梯度，拟合一颗CART回归树，得到第t颗回归树，其对应的叶子节点区域为Rtj，j=1，2，…，J。其中J为回归树t的叶子节点的个数。

4）对叶子区域j=1，2，…，J，计算最佳拟合值ctj为

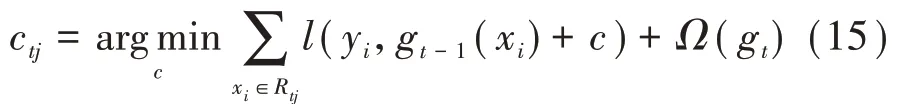
5）经T轮更新得强学习器，最终预测输出为

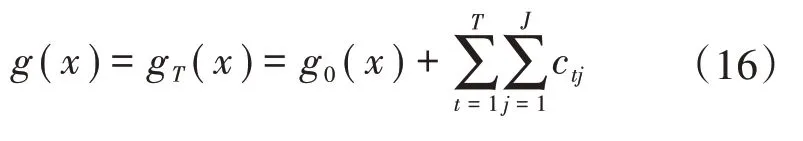
3 功率预测结果校正模型

3.1 功率预测评价标准

国家能源局规定，所有并网运行的风电场须每日定时向电网调度机构提供次日00：00—24：00 发电功率曲线，称为日前功率预测，属短期功率预测范畴。评价标准如式（17）—式（18）所示。

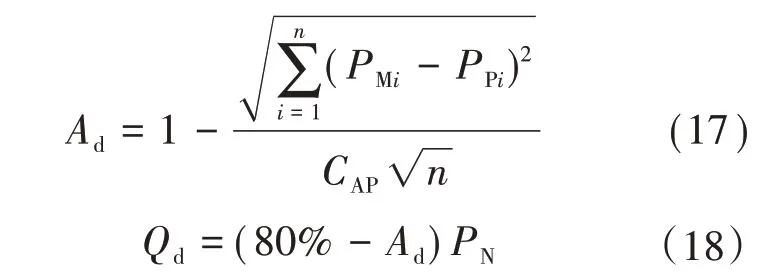
式中：Ad为日前准确率；Qd为日前考核电量；n为一天的预测个数（一般取96，即预测时间分辨率为15 min）；PMi为i 时刻的实际功率；PPi为i 时刻的日前功率预测值；CAP为风电场可用容量；PN为风电场装机容量。

对于长时间（nd天），其评价函数为准确率ACC和考核电量QCE，计算公式为：

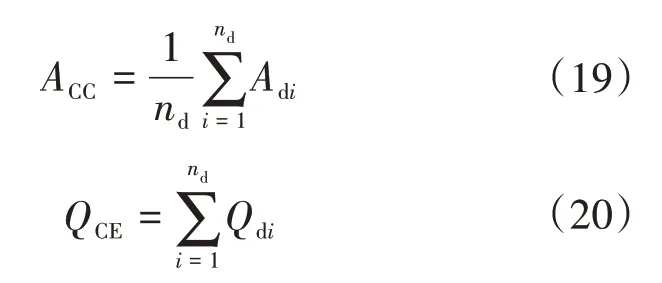
式中：Adi为第i天日前准确率；Qdi为第i天日前考核电量。

3.2 RELM功率校正模型

相较于传统神经网络，极限学习机（Extreme Learning Machine，ELM）具有结构简单、学习能力好、泛化能力强等优点。如图2，RELM 网络在传统ELM 模型的基础上引入正则化系数，可一定程度上提高功率预测模型的精度［18］。

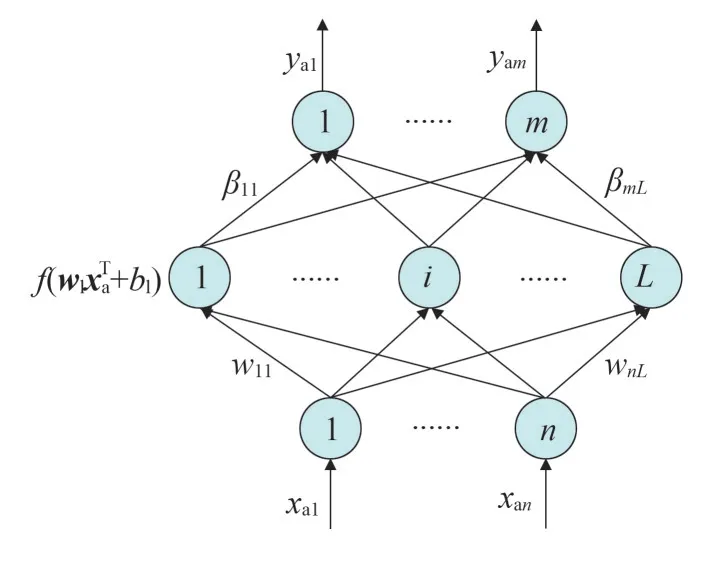
图2 RELM结构

风电场各风机风速进行机组分类后，经XGBoost模型得多组子类的预测风速，视该若干组风速为风电场内的差异特征，作为RELM 模型的输入。同时由初步功率预测模型获取预测功率计算预测功率与实际功率之差，将功率残差作为RELM 模型的学习目标，预测需校正的功率，获得最终的预测功率。

设xa为“机组分类”实验的预报风速，d′为“单一风速”实验的预测功率与真实功率的残差，f 为激活函数，则RELM的输出函数为：

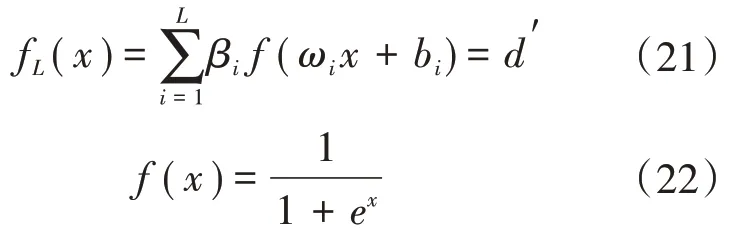
式中：ωi和βi分别为输入、输出向量与第i 个隐含层神经元之间的连接权值；bi为第i 个隐含层神经元对应的偏置值，L为隐含层个数。

将式（21）写成矩阵形式，有：

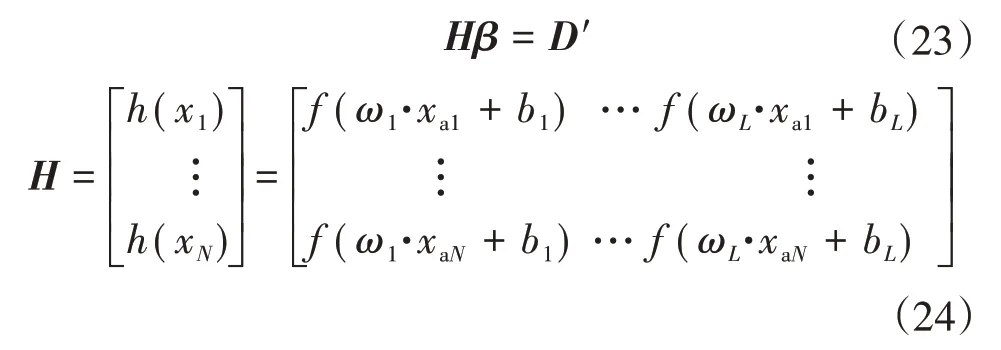
式中：β为输出向量与隐含层神经元之间的连接权值向量；D′为残差矩阵；H为激活函数矩阵。

引入正则项，得RELM的目标函数为

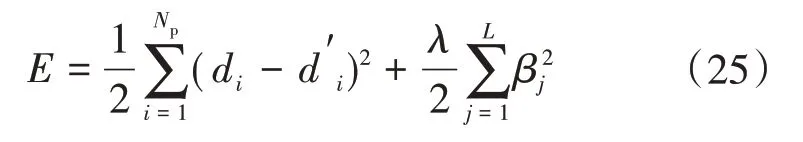
随机确定输入权值矩阵ω 以及偏置向量b，由式（23）—式（25）可得最优输出权值矩阵为

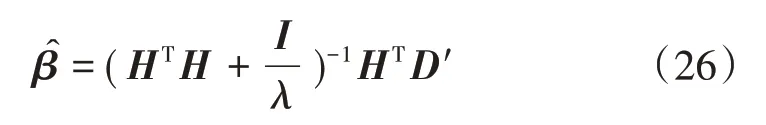
式中：I为单位矩阵。

根据初始预测功率P1与最优残差预报，得最终预测功率P3为

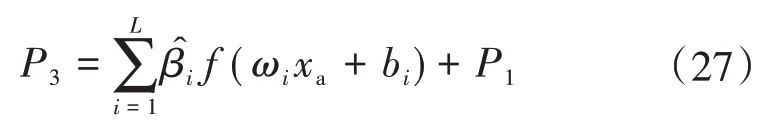
4 算例分析

4.1 风电场详情

对浙江某海上风电场开展研究，其中有效试验数据为2019-07-10至2020-04-24期间的实测风速、功率数据，采样周期为15 min。该场站如图3 所示，处于近海区域，北部临近我国第一大群岛，西部为大陆架，海面糙率变化各向异质，故选择周边9个NWP信息（NWP1—NWP 3 为群岛位置）作为初步预测模型的输入特征，剔除风电场内严重缺数的风机后，本研究共筛选59 台风机数据进行研究，图3 中镂空圆点为风机所在位置。

图3 风场风机排布与周围NWP位置

4.2 机组分类结果

计算59 台风机2019 年风速数据的3 种相似性度量，并将不同的度量矩阵进行层次聚类，对聚类结果计算STDI评判标准值，如表1所示。

表1 不同聚类下的STDI值

由表1 可知皮尔逊相关系数为最优聚类的相似性度量，基于皮尔逊相关系数的聚类结果如图4 所示，最终机组分类成4 类，每一类分布情况如图5 所示，最终获得4组子类平均风速及其累计功率。

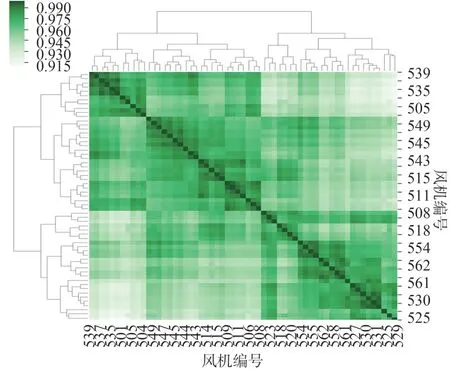
图4 基于皮尔逊相关系数的聚类结果

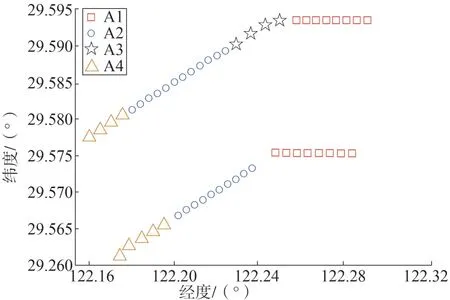
图5 不同机组子类的分布

4.3 结果分析

采用2019 年数据作为初步预测功率模型的训练数据，将2020-01-01至2020-03-01的数据同时作为初步功率模型的验证数据和校正模型训练数据，并利用2020-03-01 至2020-03-24 的数据对RELM模型进行参数调优，最终以2020-03-25至2020-04-24的数据验证模型的功率预测效果。

“单一风速”实验将风电场平均风速v0作为初步预测功率模型的输入，记为A0 组。“机组分类”实验将4 组子类（A1、A2、A3、A4）平均风速作为初步预测功率模型的输入。最后“单一风速”所得预测功率经校正模型，得“RELM 校正”实验的最终预测功率。

机组分类后，经XGBoost 的预测风速结果见表2。由于组内信息较为一致，各项评价指标较“单一风速”的风速预测结果要好，各类内的风速规律更容易被模型学习出来。由图6 可见，各子类的预报风速存在差异，在所选取的样本点中，同一时刻预报风速差异可达3～4 m/s。由此可知，风电场内存在差异信息，可利用该信息进行预测功率校正。

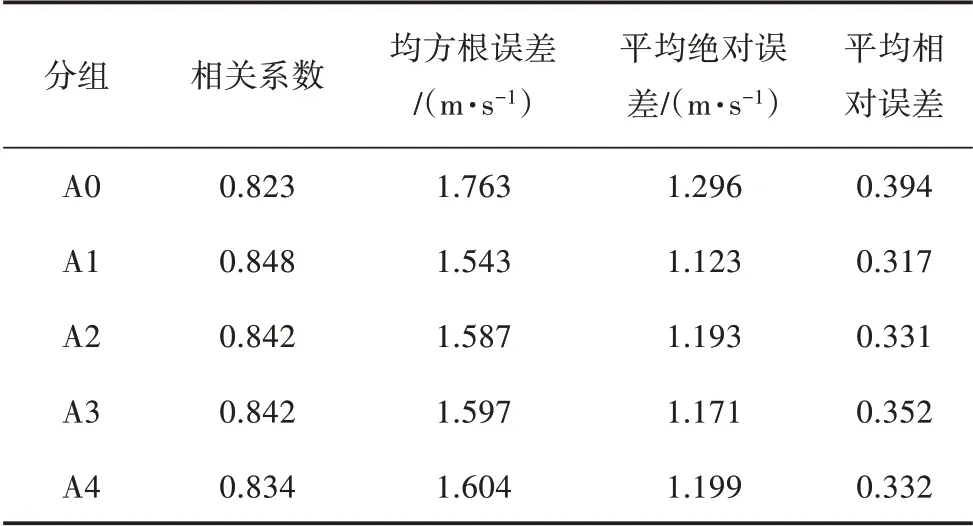
表2 风速模拟结果评价指标

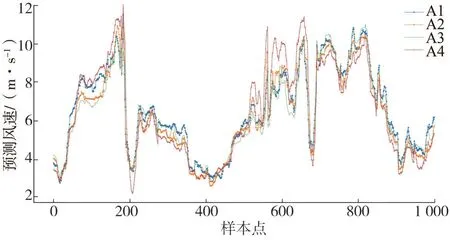
图6 四组子类预测风速对比

3 组实验功率预测结果对比如表3 所示，在训练集（为初步预测功率模型的测试集）中，“机组分类”预测功率较优，考核电量QCE下降5.36%，可见提高预测风速的准确性能有效提高预测功率的精度。经校正模型后，“REML 校正”模型长期准确率ACC有略微提升，而考核电量QCE有明显下降，相较“单一风速”下降19.24%。

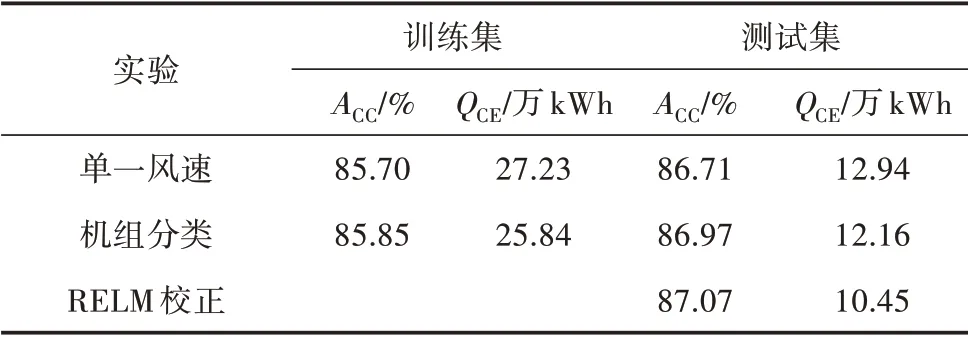
表3 不同实验的功率模拟结果对比

由于“单一风速”实验没有考虑风电场内部差异，导致个别天会极端误报，由此产生较大的考核电量。选取4月1日和4月13日典型考核天分析，如表4 所示。可知“REML 校正”可利用各机组的差异信息，有效提高预测功率的准确性，提升幅度可达3.59%。

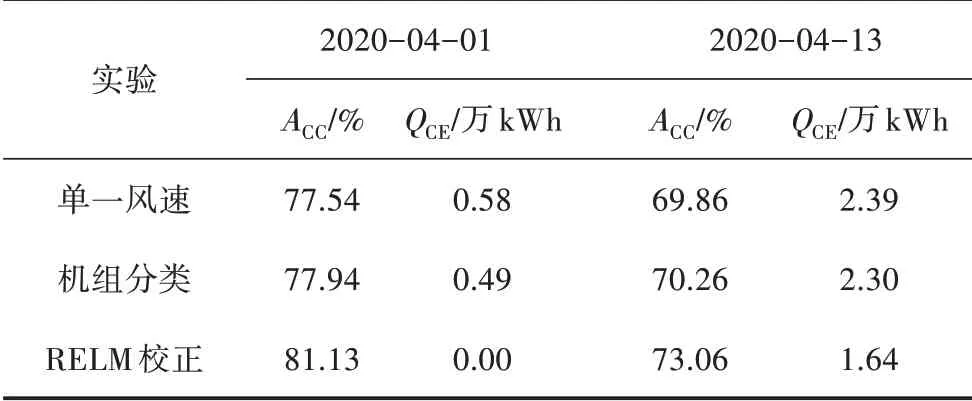
表4 选取天的功率模拟结果情况

由此表明，对于大规模风电场内部差异信息的利用有助于提高功率模型精度，避免极端误报，保证功率预测的稳定性，从而降低运行成本。

5 结语

考虑多位置NWP 数据构建初始功率预测模型，风电短期功率预测结果准确度较高，结果显示机组分类的预测功率略优于单一风速。

引入机组内部差异信息，考虑机组分类的RELM 校正预测功率，有效改善极端误报情况，降低了风电场功率预测偏差考核电量，能有效降低风电场运营成本。