基于小波分解与神经网络的光伏功率预测

王士柏，王玥娇，王 楠，孙树敏，程 艳

（国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

全球经济的快速发展对能源需求不断提高。目前，我国的主要能源供给仍是石油、煤炭和天然气，这些能源除了不可再生之外，还造成严重的环境污染，加剧温室效应［1-2］。为了应对能源短缺、减少化石燃料污染，研究可再生能源和绿色能源发电势在必行［3-4］。根据IEA（国际能源署）的报告，自2000 年以来，全球光伏发电能力以年均40%以上的速度增长，并在未来几十年具有巨大的长期增长潜力。预计到2050 年，光伏发电系统将提供全球11%的电力（4 500 TWh/a），相当于3 000 GW 的累计光伏系统装机容量［5］。

光伏发电作为具有发展前景的清洁能源之一，随着其发电技术的不断发展，光伏发电并网容量也不断增大［6-7］，因此对于光伏发电功率的预测尤为重要。光伏功率预测方法大致可分为物理方法和统计方法。物理方法以天气预报和光伏系统数据作为输入，在典型的物理方法中计算出平面阵列辐照度、模型温度，最后计算功率输出；统计方法是基于时间序列分析、因果预测、分类模型和具有历史功率测量的数据集，以及对数值天气预报、从地面或卫星图像检索的数据、太阳辐照度传感器和PV 系统数据进行统计和研究，最后得到功率［8］。统计方法模型简单，计算量小，但需要大量历史数据，无法快速反映天气的变化；物理方法不需要大量的历史数据，但建立光伏组件的模型相对复杂。文献［9-10］介绍了统计模型的功率预测方法，并对统计方法和物理方法进行了比较。实际上，为了提升光伏发电功率预测的精确度，在实践中这两种方法可以结合使用。

现有研究主要利用神经网络进行功率预测，或者通过预测相关参数的方法来得到I-V 曲线［11］。为提高光伏功率预测结果的准确性与普适性，文献［12］提出基于泄漏积分型回声状态网络（Leaky⁃Integrator Echo Sate Network，LIESN）的具有在线学习功能的预测方法。Karatepe 等人使用人工神经网络（Artificial Neural Network，ANN）方法对光伏电池组件进行建模，进而利用人工神经网络对参数进行预测，得到组件模块的电流和电压［13-14］。同时，也可根据改进电导增量法来对光伏电池最大功率点进行跟踪研究［15］。可以看出，神经网络与各种数学模型相结合可以有效提高预测精度，并已成为目前研究光伏功率预测的主流方法。

在光伏发电过程中，光辐照度、外界温度与功率之间存在显著的相关性，因此，目前大部分预测研究将辐照度和温度作为神经网络方法的输入。实际上，根据相关性理论分析，气压、湿度等因素也与光伏输出功率存在一定的相依特性。小波分解技术能够将数据分成不同的频率，对不同频率的数据输入到神经网络进行训练，因此，提出一种基于小波分解与神经网络的光伏功率预测方法，在考虑更多天气预报因素的同时，使用神经网络结合小波分解的技术来提升光伏功率的预测精度。

1 神经网络与小波分解理论

1.1 光伏功率与天气的相关性

现有研究认为光伏电站的输出功率主要与辐照度和温度有关，但其也受风速、气压、湿度、风向等其他环境参数的影响［16-17］。

LIU Luyao等人给出了不同环境因子与功率的相关性的准确数据［18］，如表1所示。

表1 环境因子对功率的影响

1.2 预测光伏输出性能的神经网络

采用BP算法的多层感知器是应用最广泛的神经网络。一般将单隐含层的前馈网络称为三层感知器，包含输入层、隐含层和输出层，如图1所示。不同的神经网络在迭代时的计算量不同，神经网络越小，计算量越小，可避免在解决预测问题时出现过拟合现象［19］。但神经网络过小，将导致预测的精度不够准确，因此需要反复试验确定神经网络隐含层的数量。

神经网络的神经元模型由一组称为突触的连接组成，每个突触都有相应的权重。在对所有加权输入求和之前，这个权重要乘以其输入层对应的输入变量xi（i 为输入层的神经元编号），并加一个输出层外部偏差负责降低或增加总和的输出（k 为输出层的神经元编号，图1 中输出层有1 个神经元），然后对该输出应用激活函数f2进行映射，将输出信号的幅值范围减小到一个有限值。激活函数可以给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中，处理复杂的问题。

图1 神经网络理论

图1中，辐照度、温度、风速、风向、气压、湿度，分别用x1，x2，…，x6表示。将输入向量X=［x1，x2，…，x6］应用于网络输入层，如图1 所示。隐含层第j 个神经元的净输入为

式中：j为隐含层神经元的编号；wji为输入层的第i个变量（i=1，2，…，6）对隐含层的第j个单元（j=1，2，…，20）的权重，其大小由神经网络训练过程自动获得；为隐含层神经元j的偏置。

图1中，f1为输入层与隐含层之间的激活函数

式中：tansig为双曲正切S型传输函数。

隐含层神经元j的输出为

输出层神经元的净输入为

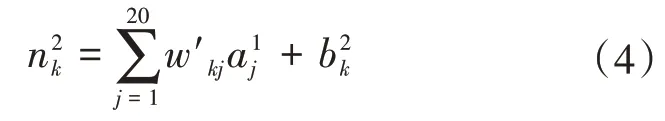
式中：w′kj为隐含层第j个单元与输出层第k个单元间的权重，图1 中神经网络输出层为1 个神经元，因此k=1；为输出层神经元的偏置。

f2为隐含层与输出层之间的激活函数，选取斜率为1的purelin线性传输函数

1.3 小波分解基本原理

在分析时间序列信号时，可以用小波变换方法来分析非线性和非平稳信号。平方可积函数是小波变换的基础，所以小波变换可以将信号分解为不同尺度层，并且分解后具有不同的分辨率。小波变换提供了给定信号的局部表示，因此适用于分析具有变化时频分辨率的信号，如光伏电站的输出功率［20-22］。小波变换的数学定义如下。

给定x（t）为平方可积信号，满足

给定一个函数ψ（t）

则x（t）的连续小波变换为

式中：CWTx(a，b)为连续小波变换；a、b 为母小波基函数的变换参数，a 为尺度因子，b 为时移；Ψa，b(t)为母小波基函数，(t)为Ψa，b(t)的共轭。

通过a 和b 的选择，小波变换提供了一种算法，即小波技术，将信号分解成具有不同时间和不同频率分辨率的低频层和高频层。

小波分解将给定信号x（n）分解为详细的平滑层。由于光伏电站的功率输出信号中含有由太阳辐射波动引起的跳变，因此具有非线性和周期性特征。利用小波分解方法，将光伏电厂的输出功率分解为两部分：信号的平滑部分与信号的详细部分。因此，小波分解方法可以从原始信号中分辨出干扰，并能分别进行分析。

1.4 预测过程

首先利用小波分解将环境因子分解为高频和低频部分，然后对低频和高频部分别输入到神经网络中进行训练，得到结果后再进行小波重构。预测过程如图2 所示。ANN1 为训练低频数据，ANN2 为训练高频数据。

图2 预测过程

2 试验数据的选择

2.1 数据来源

试验数据选自山东省某集中式光伏电站。从2018年9月至2019年6月，全天24 h进行监测得到的数据，用于训练神经网络和预测05：00：00—19：00：00这一光伏输出主要时间段的功率。每天约有1 500个监测点。这些环境因子包括太阳辐照度、温度、湿度、气压、风向、风速，测量时间间隔从几毫秒到1 s之间。

2.2 数据的选择和数据分布

监测周期约为10 个月，基本涵盖了一年的各个季节。从不同季节、不同天气中随机选取600 条数据，保证通过训练得到的神经网络具有随机性和普遍的适用性。为了更直观地看到所选数据的分布情况，证明网络的有效性，图3（a）—图3（c）以二维图的形式给出了3 种天气参数的训练值分布。从每个季节中随机抽取约3 000 个值（所选数据不包括训练数据集）作为验证数据，来验证网络预测的准确性，如图3（d）—图3（f）所示。

图3 训练数据与预测数据分布

由图3 可以看出，训练数据的分布范围较大，预测的数据没有超过训练数据的分布范围，说明了训练网络的有效性。

2.3 小波分解

对6个输入量进行小波分解，将每个变量分解为高频系数和低频系数。结果如图4—图9所示。

图4 辐照度小波分解示意

图5 湿度小波分解示意

图6 气压小波分解示意

由图4—图9 可以看出，通过一维离散小波分解对光伏电站辐照度信号、湿度信号、气压信号、温度信号、风速信号、风向信号等进行小波分解，并将低频层与高频层进行对比。每张图像均显示了小波分解之后的低频层和高频层。通过对比可知，小波分解后每个信号序列的低频部分具有平稳特性，平滑后的信号层可以表示原始信号的主要低频信息，具有良好的逼近性。而高频层信号的周期性更加明显，同时对高频干扰噪声进行了较好的滤波。

图7 温度小波分解示意

图8 风速小波分解示意

图9 风向小波分解示意

2.4 对称平均绝对误差百分比

在验证过程中，为了比较网络预测的性能，使用对称平均绝对百分比误差来度量误差，对称平均绝对百分比误差SMAPE和平均绝对百分比误差MAPE计算公式分别为：

式中：n 为验证数据的个数；At为第t 个实际值；Ft为第t个预测值。

3 试验验证

3.1 神经网络节点数的选择

不同的神经网络在迭代过程中的时间和计算量也不同。在选择神经网络进行预测时，神经网络节点数量的选择对预测精度和计算时间影响较大。对于不同问题的预测可以使用不同的神经网络，隐含层数也可以不同，有时候确定隐含层的数量是一个反复试验的过程。

测试不同节点数对网络精度的影响，如图10所示。

图10 神经网络节点个数对网络精度的影响

由图10 可以看出，当节点数量增加到约13、14个节点时，网络的准确率得到了显著提高。随着节点数量的不断增加，神经网络的误差稳定在3.5%左右。然而，随着节点数量的增加，网络越来越复杂，训练时间也越来越长，但准确率没有明显提高。考虑到训练时间和网络的准确性，神经网络的隐含层节点数选择20个。

3.2 试验结果分析

为了方便起见，第1 种神经网络预测方法简称ANN，第2种小波分解与神经网络相结合的方法简称WDANN。两种方法的误差对比如表2 所示。由表2可知，小波分解与神经网络相结合的预测方法比神经网络预测方法更准确。

表2 两种预测方法误差对比 单位：%

为了更具体地分析结果，对上述两种方法和3 000 个预测数据进行了不确定性分析，如图11 所示。图11 中，上四分位数表示从最小到最大排名为75%的值，下四分位数表示从最小到最大，排名为25%的值，上下限表示除异常值外的所有误差值的范围。由图11 可以看出，与神经网络预测的数据误差分布相比，小波分解与神经网络相结合的方法更加紧凑和准确，误差的中位数和平均值显著变小。

图11 预测数据误差对比分析

预测功率和实测功率的分布如图12 所示。图12中，蓝点的横坐标表示归一化后的实测功率，蓝点的纵坐标表示归一化后的预测功率，实线表示比例函数曲线。预测的结果越精确，则预测功率越接近于实测功率，大量数据分布应越接近y=x 的函数曲线。对比图12 可知，WDANN 预测结果较ANN 预测结果的分布更接近于y=x，所以可以直观地看出WDANN比ANN预测的更加准确。

图12 实测功率与预测功率分布

4 结语

提出了一种将人工神经网络与小波分解相结合的光伏系统功率的预测方法。在同时考虑神经网络训练精度和时间消耗的基础上，确定了神经网络训练精度更高、速度更快的隐含层节点数。研究了不同节点数对神经网络精度的影响，选取精度好且训练时间短的点作为隐含层数，对光伏功率进行预测。

所提方法将不同的环境因子分为低频和高频两类，然后用小波变换对预测的低频功率和高频功率进行重构，最后合成预测功率。该方法将小波分解与神经网络相结合，比单纯使用神经网络进行功率预测具有更高的精度。通过试验验证了模型可以有效准确地预测光伏发电系统的输出功率，提高了电网的安全性和稳定性。