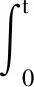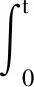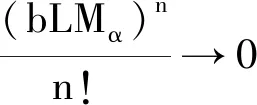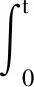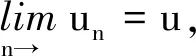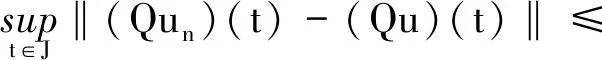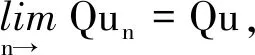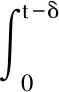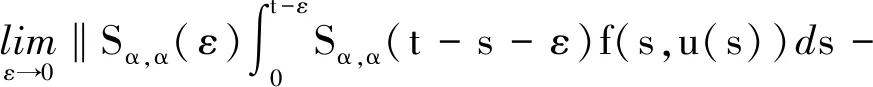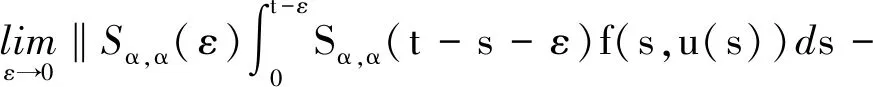一类分数阶发展方程柯西问题mild解的存在性
陈 燕
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
整数阶微分方程在很多学科领域中起着非常重要的作用,而相比于整数阶微分方程,分数阶微分方程由于它的记忆性和遗传性能更精确地描述实际问题.近年来,分数阶微分方程已被应用在很多学科领域,如粘弹性力学、分数物理学、动力系统控制理论、混沌与湍流、反常扩散、信号处理等[1-4].
因此,越来越多数学学者开始研究分数阶发展方程,进而其相关理论也越来越深厚.各类分数阶发展方程解的存在性和唯一性也受到了广泛的研究[5-9].
文献[10]利用预解算子族{Sα,β(t)}t≥0的性质研究了如下一类分数阶发展方程mild解的渐近性及可积性.
(1)
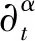
Caputo分数阶导数是在1967年由Caputo提出的,参见文献[11],它的定义如下:
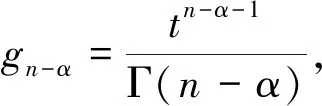
本文将在Banach空间中研究下列分数阶发展方程
(2)
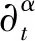
本文运用Laplace变换法、Banach压缩映射原理以及Shauder不动点定理等方法证明了该类方程mild解的存在性与唯一性.
1 预备知识
设(X,‖·‖)是Banach空间,B(X)是由X→X的所有有界线性算子全体构成的空间.C(J,X)表示定义在区间J上取值于X上的连续函数全体构成的Banach空间,其范数定义为
‖x‖C=sup{‖x(t)‖,t∈J}.
可测函数x:J→X称为Bochner可积,当且仅当t→‖x(t)‖是Lebesgue可积的.
L1(J,X)表示定义在区间J上取值于X上的Bochner可积函数全体构成的Banach空间,其范数定义为
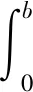


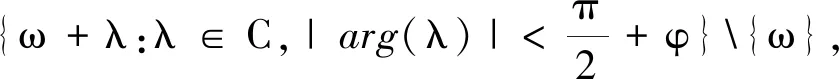
且
则称A关于角φ是ω-扇形的.
定义1[10]设A:D(A)⊂X→X为闭的线性算子,1≤α≤2,且0<β≤2,如果存在ω≥0及强连续且指数有界的算子族
Sα,β:[0,∞)→B(X),
使得
{λα:Reλ>ω}⊂ρ(A),
对∀x∈X,有
(3)
及
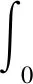
(4)
则称A是(α,β)-预解族的生成元,称{Sα,β(t)}t≥0是由A生成的(α,β)-预解族,其中γ是合适的复路径.
引理1[10]设1≤α,β≤2,Sα,β是由A生成的(α,β)-预解族,则
(1)对∀x∈D(A),t≥0,有
Sα,β(t)x∈D(A),Sα,β(t)Ax=ASα,β(t)x.
(2)如果x∈D(A),t≥0,则
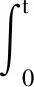
(5)
(3)如果x∈X,t≥0,那么
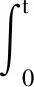
且
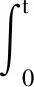
(6)
特别地,Sα,β(0)=gβ(0)I.

(7)
记
(8)

类似于文献[12],可以得到以下结论.
引理4设对于任意t>0,{Sα,β(t)}t≥0按一致算子拓扑连续,如果Sα,β(t)是紧的,则有
(9)
证明设‖x‖≤1,t>0以及ε>0.由于Sα,β(t)是紧的,则集
Wt:={Sα,β(t)x:‖x‖≤1}
也是紧的.那么存在一列有限族
{Sα,β(t)x1,Sα,β(t)x2,…,Sα,β(t)xm}⊂Wt,
使得对∀x,有‖x‖≤1,那么存在xi(1≤i≤m),使得
(10)
由Sα,β(t)的强连续性,t≥0,知存在0 (11) 另一方面,由于Sα,β(t)按一致算子拓扑连续,所以存在0 (12) 因此,对0≤k≤min{h1,h2}以及‖x‖≤1,根据式(10)~(12)即得, 则对∀t>0,式(9)成立. 由引理4可以得出如下结论. 引理5设对于任意t>0,{Sα,β(t)}t≥0按一致算子拓扑连续,如果Sα,β(t)是紧的,那么有 (13) 证明设t>0且0 ‖Sα,β(t)-Sα,β(h)Sα,β(t-h)‖≤‖Sα,β(t)-Sα,β(t+h)‖+‖Sα,β(t+h)-Sα,β(h)Sα,β(t)‖+‖Sα,β(h)Sα,β(t)-Sα,β(h)Sα,β(t-h)‖≤‖Sα,β(t)-Sα,β(t+h)‖+‖Sα,β(t+h)-Sα,β(h)Sα,β(t)‖+M‖Sα,β(t)-Sα,β(t-h)‖. 由引理4及Sα,β(t)的连续性得该式成立. 考虑下面的分数阶线性发展方程 (14) 其中f(t)∈L1(J,X),对此方程两边做Laplace变换,左端为 则 整理可得 (15) 将式(4)代入式(15),可得 因此有 其中Sα,α(t)*f(t)表示Sα,α(t)与f(t)的卷积. 定义2如果函数u∈C(J,X),对任意t∈J,有 (16) 则称u是方程(2)的mild解. 本文中,令r>0,为有限常数,记Br={u∈C(J,X):‖u‖C≤r}. 本文主要结论的证明要用到如下两个结论. 定理1(Shauder不动点定理)如果V是Banach空间X的一个有界凸闭子集,如果T:V→V是全连续算子,则T至少存在一个不动点x*,使得Tx*=x*. 定理2(Banach压缩射原理)设V是Banach空间X的有界闭子集,如果T:V→V满足∃0<α<1,∀x,y∈V,使得 ‖Tx-Ty‖<α‖x-y‖, 那么T在X上存在唯一的不动点. 注:若存在自然数n使得Tn是X上的压缩映射,那么T在X上存在唯一的不动点. 下面给出几个假设条件,以方便定理的叙述和证明: (Hf)f:J×X→X满足: (1)f(t,·):X→X对几乎处处t∈J连续,f(·,x):J→X对x∈X可测. (2)存在函数φ∈L1(J,R+),使得‖f(t,x)‖≤φ(t),t∈J. (3)f(t,x)关于x满足Lipschitz条件,即∃L>0,使得 ‖f(t,x2)-f(t,x1)‖≤L‖x2-x1‖,∀t∈J,x1,x2∈X. (HS):由A生成的预解算子族{Sα,β(t)}t≥0是紧的. 定理3假设条件Hf(3)满足,则方程(2)在区间J上存在唯一的mild解. 证明定义算子Q:C(J,X)→C(J,X),满足 (17) 显然u是方程(2)的mild解等价于u是算子Q的不动点. ∀u1,u2∈C(J,X),由Hf(3)及式(8)可得 累次使用该不等式可得 所以有 (18) 定理4假设条件Hf(1)、(2),HS都满足,则方程(2)在区间J上至少存在一个mild解. 证明如式(17),定义算子Q:C(J,X)→C(J,X).取r>0,满足 M1‖x‖+M2‖y‖+bMα‖φ‖L1(J,R+)≤r. (19) 第1步:证明Q(Br)⊂Br. 对任意u∈Br,t∈J,有 (20) 由Hf(2)及式(8)可得 ‖(Qu)(t)‖≤M1‖x‖+M2‖y‖+bMα‖φ‖L1(J,R+). (21) 所以有 ‖Qu‖C≤r. (22) 第2步:证明Q是连续算子. 第3步:证明Q是紧算子. 首先证明对任意的t∈J,V(t)={(Qu)(t):u∈Br}是X中的相对紧集.显然,当t=0时,V(0)是X中的相对紧集.当t∈(0,b]时,对∀ε∈(0,t)及u∈Br,定义算子Qε如下: (23) 对∀δ∈(ε,t),有 由引理5可得,对s∈[0,t-δ],当ε→0时, Sα,α(ε)Sα,α(t-s-ε)-Sα,α(t-s)→0, 且有 (24) 由δ的任意性及控制收敛定理可得 (25) 另一方面, 因此, (26) 那么,由完全有界性可得 在X中是相对紧的.这意味着存在一族相对紧集{Vε(t)}0<ε 下面证QBr是等度连续的. ∀u∈Br,0≤t1≤t2≤b,有 因此,由预解算子族{Sα,β(t)}t≥0的强连续性知,当t2-t1→0时,容易验证‖(Qu)(t2)-(Qu)(t1)‖→0,从而对t∈J,QBr是等度连续的.由Arzela-Ascoli定理可得Q为紧算子.由Shauder不动点定理知Q至少存在一个不动点,即方程(2)在区间J上至少存在一个mild解.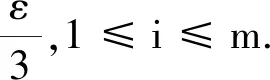
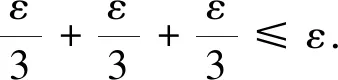
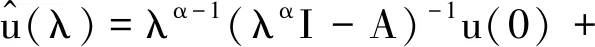
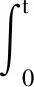
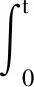
2 主要结论