高度差:解决最值问题的一个传奇

杭州第十四中学(310006) 朱成万

近年来,求函数的值域或最值,或者代数式的最值问题,试题越来越灵活、越来越难,对学生的能力要求越来越高.所以透彻地理解问题本质,合理选择解题方法和解题工具显得尤为重要,选择不恰当,费时、费力,且不得要领.

本文将探讨用“高度差”破解最值问题,这是借助函数图象,从形的角度解题,能减少运算量,直入问题核心,使题目变得简单易懂.下面以近几年的学考题、高考题和竞赛题为例,阐述“高度差”在解题中的妙用.

一、学考题难,思路何在

例1(2016年浙江省学考第18 题) 设函数f(x) =,x ∈[1,2](a,b ∈R).若对任意的正实数a和实数b,总存在x0∈[1,2],使得f(x0) ≤m,求实数m的取值范围.

本题中f(x) 是含参数的绝对值函数,涉及到任意和存在问题,需先求x ∈[1,2] 时f(x) 的最大值M(a,b),进而求a >0,b ∈R 时M(a,b) 的最小值,即这是一道综合性强、难度较大的题目.

思路一:分类讨论

令u(x) =−ax −b(a >0),则u(x) 在区间[1,2]上单调递减.它的图象可能出现三种情形:在图1 中M(a,b) =u(1); 在图2 中M(a,b) =u(2); 在图3 中,由于对u(x)图象进行翻折之后,f(x)的最大值在x= 1 或2处取到,所以需对两个端点的函数值进行比较,再次分类讨论(讨论略).

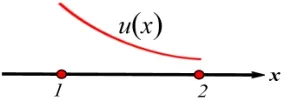
图1

图2

图3

求出f(x)的最大值M(a,b)后,再将a,b作为变量,求M(a,b)的最小值(解法略).显然,这种方法运算量大,费时、费力,在学考有限时间内难以完成.

思路二:绝对值三角不等式

从思路一的讨论可知,f(x)的最大值只能在x= 1 或x=2 处取到,则

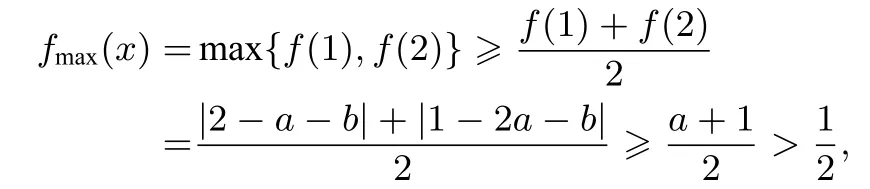
这种方法技巧性强,对学生的能力要求较高,有的学生即使进行了大量的训练,也不一定能掌握.

思路三:高度差

构造函数g(x) =,h(x) =ax+b,则f(x) =|g(x)−h(x)|.如图4 所示,f(x) 的几何意义是对于每个x来说,函数g(x)和h(x)图象上两点之间纵坐标的差距,即纵向距离,也称“高度差”.

图4

直线h(x) 的两个参数a,b都在变化,b的变化表示直线可上下平移,a的变化表示直线可旋转.在运动过程中,显然当a趋向于0 时,即h(x) 处于图5 所示的位置时,最大高度差就是g(x) 最大值与最小值之差的一半,即

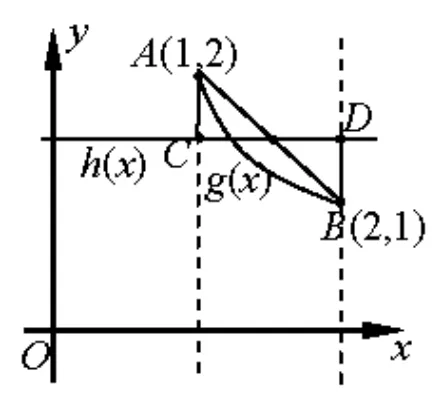
图5

例2(2015年浙江省学考第34 题) 设函数f(x) =若对任意实数a,b,总存在实数x0∈[0,4],使得f(x0)≤m,求实数m的取值范围.

类同例1 的分析,该题也可转化为求m≤则f(x)的几何意义是函数g(x)和h(x)最大高度差的最小值.

如图6 所示,直线OA的方程是平行于OA且与g(x)相切的直线BC的方程是则两条平行线OA与BC正中间的那条平行直线就是使得最大高度差达到最小的直线h(x).此时,最大高度差为两条平行线OA与BC纵截距之差的一半,故

图6

二、高考常考,一脉相承

用“高度差解决有关最值问题的方法,在高考中也经常出现,下举几例.

例3(2008年高考浙江卷第15 题)已知t为常数,函数y=｜x2−2x −t｜在区间[0,3]上的最大值为2,则t=____.

分析把函数表达式化为y=｜(x −1)2−(t+1)｜,其几何意义为函数y= (x −1)2,x ∈[0,3] 图象上任一点到y=t+ 1 的“高度差”,如图7 所示,满足= 2 的t+ 1 只能等于2,所以t=1.

图7

例4(2017年高考浙江卷第17 题) 已知a ∈R,函数在区间[1,4]上的最大值是5,则a的取值范围是____.

分析f(x) 在区间[1,4] 上的最大值是5,即令u(x) =|x+−a|,则其几何意义是曲线y=x+与直线y=a的高度差.如图8 所示,函数y=x+在区间[1,4]上是平口单峰函数,它与直线y=a最大高度差的最小值为此时a=时,,所以a≤

图8

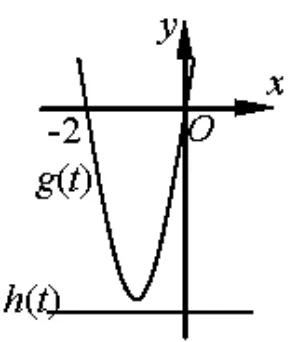
图9

例5(2019年高考浙江卷第16 题) 已知a ∈R,函数f(x) =ax3−x,若存在t ∈R,使得|f(t+2)−f(t)|≤则实数a的最大值是____.

解法1f(t+2)−f(t)=a(t+2)3−(t+2)−(at3−t)=2a(3t2+6t+4)−2,由题意得|3at2+6at+4a −1|≤即

令g(t) = 3at2+6at,h(t) = 1−4a,则①的几何意义是函数y=g(t)图象上存在一点到y= 1−4a的“高度差”的绝对值的最小值为当函数g(t)与h(t)的图象相交时,显然成立;当函数g(t)与h(t)的图象不相交时,如图9 所示,显然当t=−1 时符合题意,即|−3a −(1−4a)|≤解得

解法2f(t+2)看作是f(t)的图象往左平移两个单位,则|f(t+2)−f(t)|可看作y=f(t+2)与y=f(t)的高度差.

若函数图象相交,如图10 所示,则高度差最小值为0,符合; 若函数图象不相交,如图11 所示,要使在x=t处“高度差”最小,则两曲线在x=t处的切线平行,即f′(t+2)=f′(t),则3at2−1=3a(t+2)3−1,解得t=−1,所以|f(1)−f(−1)|≤

图10

图11

三、竞赛参和,方法雷同

这类试题不仅在学考、高考中出现,在数学竞赛中也经常出现,解题方法与前述是一致的.这同时也说明了,这类题型是一个常见的题型,有研究的价值.

例6(2010年全国高中数学联赛第9 题) 函数f(x) =ax3+bx2+cx+d(a ̸=0),当0 ≤x≤1 时,|f′(x)|≤1,试求a的最大值.

解由题知f′(x) = 3ax2+2bx+c,不妨设a >0,令g(x) = 3ax2,h(x) =−2bx −c,则f′(x) =g(x)−h(x),它的几何意义是g(x) 与h(x) 的高度差,如图12 所示.直线OA方程:y= 3ax,与OA平行且与g(x)切于B点的直线方程:y= 3ax −两者最大高度差的最小值为所以所以a的最大值为

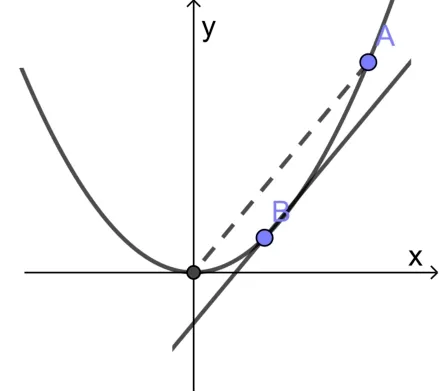
图12

例7(2017年全国高中数学联赛第9 题) 设k,m为实数,不等式|x2−kx −m|≤1 对所有x ∈[a,b]成立,证明:

解设f(x)=|x2−(kx+m)|,则f(x)表示函数y=x2与y=kx+m的高度差,由题知,如图13 所示,直线AB的方程为y=(a+b)x−ab,与AB平行且过点C的切线方程为y= (a+b)x −所以最大高度差的最小值为故只需,所以b −a≤

图13

四、追本求源,最佳逼近

利用“高度差”解决此类函数最值问题,它的根源是切比雪夫最佳直线逼近原理.设函数f(x) =|g(x)−(ax+b)|(a,b ∈R)在区间[m,n]上的最大值的最小值为T,其中g(x)是在[m,n]上的连续单峰函数.则:

(1) 若g(m) =g(n),设g(x) 的最值点为x0,则T=当a= 0,b=时取到最大值的最小值,前述例1,例3,例4 就是这种情况.

(2)g(m)̸=g(n),设过A(m,g(m)),B(n,g(n))两点的直线方程为:y=kx+b1,与g(x)相切且平行AB的直线方程为:y=kx+b2,则T=当a=k,b=时取到最大值的最小值.前述例2,例6,例7 就是这种情况.

五、平时练习,变式拓展

上述用高度差解决的是“最大值的最小值”问题,典型特征是带有绝对值,即函数f(x)可以表示为|g(x)−(ax+b)|.实际上,高度差并不局限于上述题型,它有着广泛的应用.任何一个函数都可以表述成两个函数之差,即f(x) =g(x)−h(x),所以任意一个函数f(x) 都可以看作是两函数g(x)与h(x)的高度差.

例8求函数f(x)=x+的值域.

分析函数f(x) =可看成是曲线与直线y=x的高度差,如图14 所示.当时,高度差的最小值为故值域为

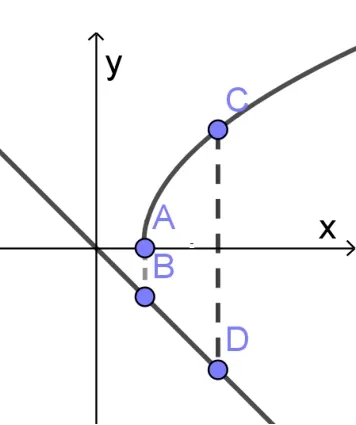
图14

例9(2020年高考全国Ⅱ卷理科第23 题) 已知函数f(x)=｜x −a2｜+|x −2a+1|.

(1)当a=2 时,求不等式f(x)≤4 的解集;

(2)若f(x)≤4,求a的取值范围.

解令g(x) =｜x −a2｜,h(x) =−|x −2a+1|,则f(x)的几何意义就是函数g(x)和h(x)图象上两点之高度差.

(1)由图15 知,当x≤或x≤时,高度差f(x) ≤4.

图15

(2)由图16 知,要使高度差f(x) ≤4,则需a2−(2a −1)≤4,解得a≤−1 或a≤3.

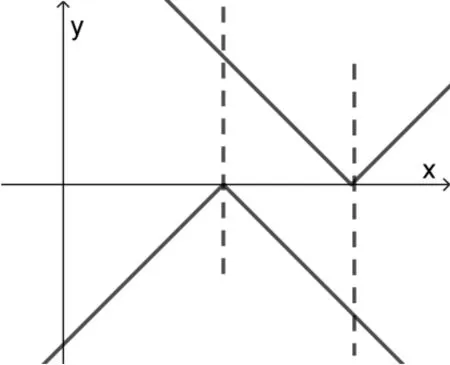
图16

六、题后反思,至精至简

高考真题是专家们精心研究之成果,学考题、竞赛题也是如此.它所承载的思想方法和核心素养深厚,对教学有引领作用,解题思路的获得,问题本质的理解,与学生的数学能力和数学素养息息相关.本文用“高度差”解答学考、高考、竞赛题,是从形的角度入手,以形驭数,能提升学生的数形结合能力,提升直观想象的数学核心素养.

基础数学的本质都是“精简朴实的,它们的根源都是自然而富有直观的内涵.”高考、学考、竞赛题目也是如此,表面看纷繁芜杂,但内核的东西却简约明了.用“高度差”解决最值问题,直观形象,直入问题核心,至精至简.本文的“多题一解”,旨在帮助学生理解数学,优化解题方法,提升数学素养,发挥数学的内在的价值,以数学的方式立德树人.