基于正交设计的黏滞流体阻尼器性能仿真及参数分析

伍勇，郭有松，洪明*

1 大连理工大学 船舶工程学院，辽宁 大连 116024

2 江苏工邦振控科技有限公司，江苏 常州 213000

0 引 言

黏滞流体阻尼器（viscous fluid damper, VFD）由缸筒、活塞头、活塞杆 、密封件和黏性介质等部分组成，属于速度相关型阻尼器，具有结构简单、无刚度、速度快以及减振效果好等特点，被广泛应用于军事装备、航空航天、船舶、车辆等领域。目前，VFD的理论相对比较成熟，而准确把握各结构参数对VFD阻尼性能影响的敏感度以用于指导设计仍是当前研究的难点，与此同时，其阻尼性能的设计和参数测定仍以大量的试验为主，研发周期长、成本高。

国内外研究人员对于VFD的研究已取得诸多成果。Makris等[1]重点研究了VFD的流体动力学理论，提出了力学模型，该研究为VFD的应用设计奠定了理论基础，但未研究VFD结构参数对阻尼性能的影响。美国国家地震研究中心和加州大学伯克利分校地震研究中心针对VFD做了大量的模型试验研究。此外，美国国家科学基金会和美国土木工程学会也针对VFD组织了2次大型的联合测试：美国旧金山金门大桥联合测试和美国高速公路创新技术评估中心对比试验（HITEC）[2-3]。这些试验测试旨在证明VFD用于结构抗振的可行性和可靠性，而对于如何具体设计未做研究。对于VFD结构参数与阻尼性能间的关系，欧进萍和丁建华[4-5]构建了间隙式和孔隙式VFD的阻尼力计算公式，但未能得出各结构参数对速度指数的影响程度。陈威[6]通过控制变量法研究了VFD的结构参数对阻尼性能的影响，但因研究方案太多，效率较低，无法得出各参数对阻尼性能的敏感度。刘晓飞[7]重点研究了活塞开孔形式对VFD的速度指数的影响，而其他结构参数对速度指数的影响则未予以研究。

从上述国内外研究情况来看，对VFD的研究主要包括2类：一类是研究理论基础及其实际应用的可行性；另一类是研究各结构参数与阻尼性能间的关系。然而，目前对于VFD各结构参数对阻尼性能的敏感度，以及通过FLUENT仿真计算与理论对比分析来设计研究VFD阻尼性能的文献较为少见。

受前人启发，本文拟采用正交设计方法，研究VFD的结构参数对阻尼性能的敏感度，并优化VFD的设计方法。首先，确定各结构参数的选取范围；然后，运用正交设计表确定各参数组合，得到最具代表性的不同设计方案，通过FLUENT流场仿真计算得到各方案的阻尼系数和速度指数，并与理论计算和实测结果进行对比，验证仿真的准确性；最后，由正交设计原理得到各结构参数对阻尼性能影响的敏感度，以用于优化结构参数。

1 正交设计原理

在20世纪40年代后期，日本统计学家田口玄一（Genichi Taguchi）使用设计好的正交表（正交设计法中用于合理安排试验并对数据统计分析的一种特殊表格工具）安排试验 ，这种方法简单易行，从此正交设计在世界范围内得以普遍推广和使用[8]。正交设计是多因素的优化试验设计方法，是从全面试验的样本点中挑选出具有代表性的样本点来做试验 ，这些样本点具有均匀分散性和整齐可比性[8]。具体的实际操作就是使用正交表得到这些样本点，进而得到相应的试验方案。

以L9(34)正交表为例，L为正交表代号，9表示该表共9行，3表示每个影响因素具有3个水平取值，4表示该正交表最多安排4个因素。以图1对L9(34)进行直观解释：三维正方体由3个互相垂直的平面分割出27个交叉点，每个维度代表一个影响因素； 将每个维度分割成3份代表每个因素的水平，则全部27个交叉点代表3个因素、3个水平所需的全部试验次数。

根据正交设计思想，只需均匀分散的9个试验点。具体位置安排如下：每个平面含9个交叉点，能确保刚好有3个是正交试验点，且每条横线及竖线上分布有1个正交试验方案。图1所示为得到的含9个标记的试验点方案。以三角形标记点为例，其表示A2B2C1，即A因素取2个水平，B因素取2个水平，C因素取1个水平。

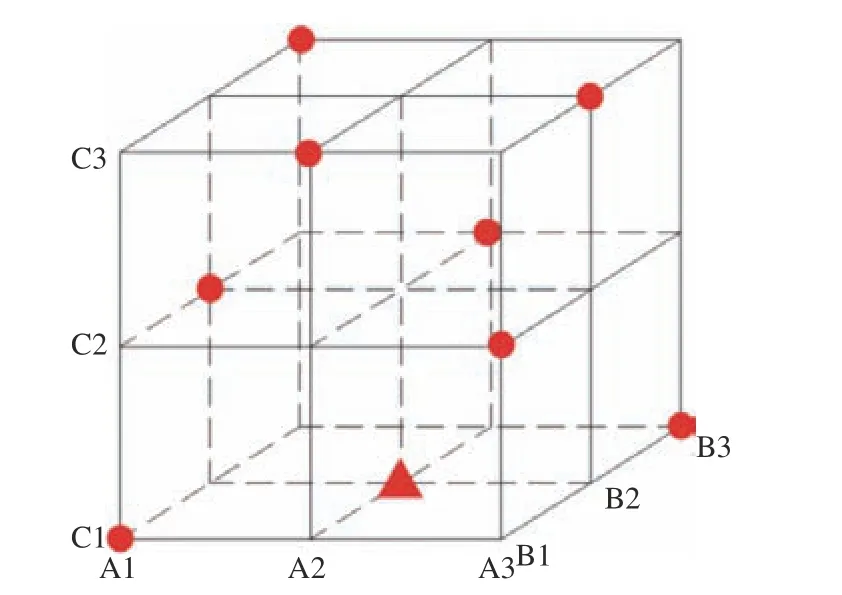
图 1 L9(34)正交表试验分布Fig.1 Experimental distribution of L9(34) orthogonal array

正交试验设计方案制定与数据处理流程如图2所示。图中，K为正交表中任一列相同水平号对应的试验结果之和，R为各水平K的平均值中最大与最小值的差值（极差），F为阻尼力。

2 物理模型

本研究设计了组合式VFD，图3所示为构建的物理模型，其由缸筒、活塞、活塞杆及内部二甲基硅油介质组成。分析中，假设阻尼器内部的二甲基硅油均匀且不可压缩，活塞杆和活塞头等为不变形的刚体，且温度恒定。图中，D0为缸筒直径，D1为活塞直径，D2为活塞杆直径，L为缸筒长度，l为开孔长度，l0为活塞厚度，r0为开孔半径，H为缸壁与活塞间隙。

图 2 正交设计流程Fig.2 Flowchart of orthogonal design

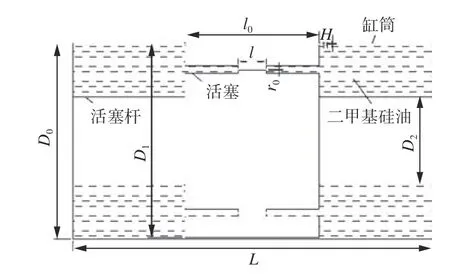
图 3 黏滞流体阻尼器结构模型Fig.3 Structural model of viscous fluid damper

3 黏滞流体阻尼器正交试验方案设计

基于前人[1,4-7,9]的研究分析，活塞上的开孔半径r0、开孔长度l、开孔个数n、活塞直径D1等是影响VFD性能的主要因素。参考某工程VFD产品的结构参数，固定因素取值如表1所示，研究选取的4个影响因素取值如表2所示。

由4因素4水平所要求的全面试验次数（≥44=256次）可见，其工作量过多，需要采用正交设计来安排试验。具体思路如下：每个方案的数据组合应保证4因素4水平的四维空间中各水平分割平面上的方案数据相互正交，每个选取的数据在统计学上具有不相关性，且均匀分散，整齐可比。具体而言，本次试验为4因素4水平试验，按正交试验思路只需安排16次试验，故选取L16(45)正交表，把试验因素安排到列，因素水平安排到行，每列不同数字出现的次数相等，任意两列及同一行中的数对出现次数相等，得到16种方案组合，并设置空列作为随机误差列。具体试验方案如表3所示。

表 1 固定因素取值Table 1 Value of fixed factors

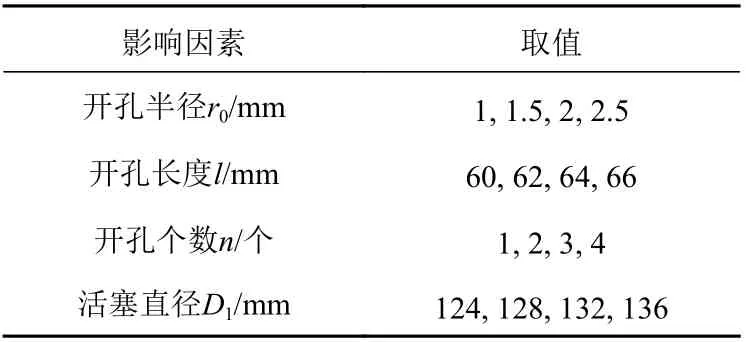
表 2 影响因素的取值范围Table 2 Value range of influence factors

表 3 正交设计方案表Table 3 Schemes of orthogonal design

4 正交设计方案计算

VFD的本构关系如式（1）所示，其阻尼特性取决于阻尼系数C和速度指数α。为研究各参数变量影响阻尼特性的程度，根据正交设计原理，C和α需要作为正交设计的评价指标。将FLUENT计算得到的速度与阻尼力曲线进行乘幂函数拟合，即可得到C和α。

式中，v为活塞运动速度。

4.1 仿真计算

4.1.1 计算方法与边界条件

仿真时，根据相对运动原理，保持活塞静止，二甲基硅油以正弦位移由左端入口进入阻尼器内部做往复流动[10]。VFD内的流体（即硅油）为非牛顿幂律流体，其本构关系[11]表示如下：

式中：τ为剪应力；k为稠度系数， Pa·sm，m为流变指数；γ˙为剪切速率。分析中，选用30万cSt黏度硅油，按文献[9]，k=2 600 P a·s0.275，m=0.275，流体密度ρ=970 kg/m3。仿真时，硅油材料黏度采用非牛顿幂律模型。经式（3）[12]及连续性方程计算，得到试验方案中的最大雷诺数在间隙和孔隙处，仅达到1.355，远远低于2 300，故选用了层流模型。

式中：D为有效直径；μ为液体介质的动力黏度。

为得到活塞面两侧压力变化，采用非稳态计算，分析中以余弦速度加载，其速度为：

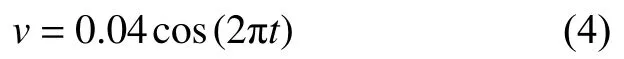
在FLUENT软件设置中：与硅油接触的边界设为固壁，即无滑移光滑边界条件；出口为压力出口；根据加载周期性，迭代时间取0.25个周期；考虑到计算速度，迭代时间步长取0.001 s。监测记录活塞两侧的瞬时绝对压力，通过其与活塞面的有效面积的乘积得到每个时刻的瞬时阻尼力。

4.1.2 网格独立性检验

对流体域进行网格划分计算时，不同网格大小对计算结果有一定的影响，故选取了如表4所示的4组网格数的模型。根据稳态计算得到的压差阻力进行网格独立性检验，结果如图4所示。随着网格数的增加，压差阻力偏差较小，可以认为达到了网格独立性要求。经综合考虑，最终选取的是计算网格数为2 091 891的计算模型。

表 4 网格独立性检验Table 4 Grid independence test

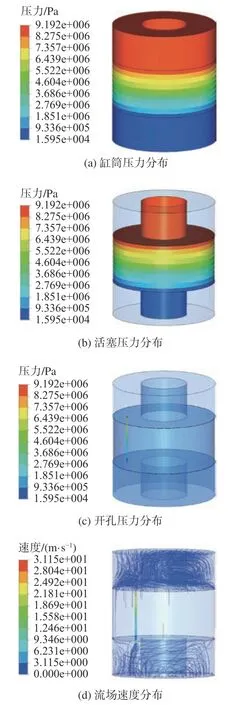
图 4 黏滞流体阻尼器性能仿真网格独立性检验结果Fig.4 Results of grid independence testing for property simulation of VFD

4.2 理论计算

根据流体控制方程，欧进萍等[4-5]构建了间隙式和孔隙式VFD的阻尼力计算模型，推导了阻尼力计算公式。

为了防止拉缸，在实际的VFD缸壁与活塞之间留有间隙。根据间隙式和孔隙式阻尼力计算公式进一步推导得到组合式（既有间隙又有孔隙）阻尼力的计算式为

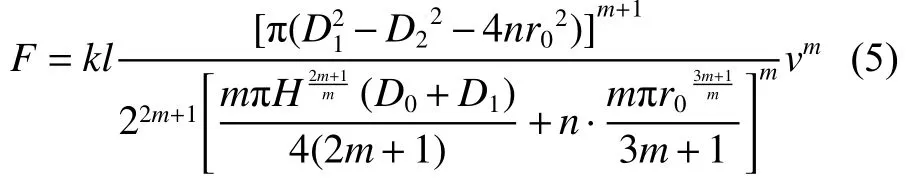
4.3 正交设计仿真、理论与试验结果分析

以方案1，8，16为例，将仿真、理论与实测结果的阻尼力和速度绘制成“力-速度”关系曲线，取0.85倍和1.15倍理论值进行对比分析，同时对“力-速度”进行乘幂函数拟合，如图5～图7所示。经比较，仿真结果与理论值的相对误差为±15%，且相比实测结果偏小，误差为±15%。

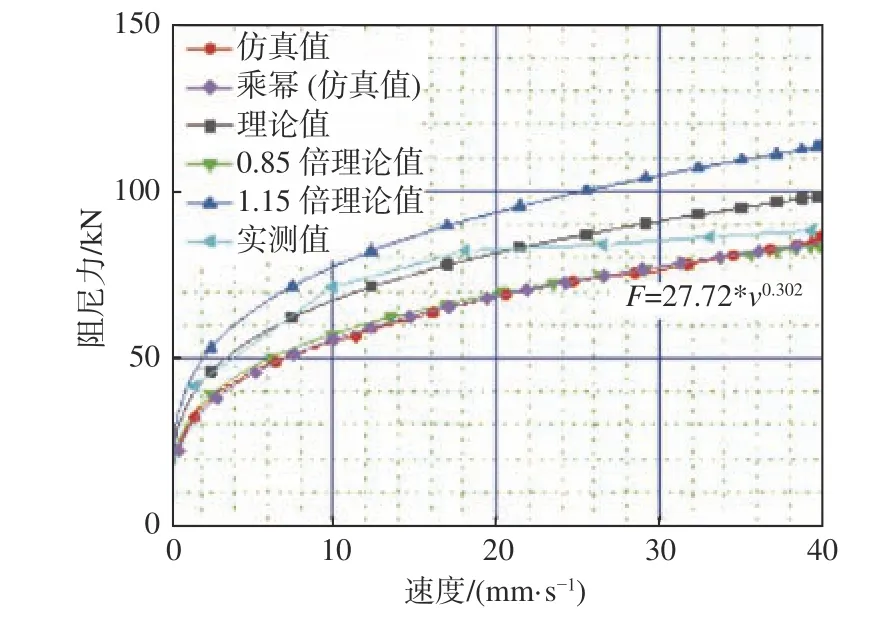
图 5 仿真、理论和试验结果的力-速度曲线（方案1）Fig.5 Force-velocity curves of simulation, theoretical and experimental results in scheme 1

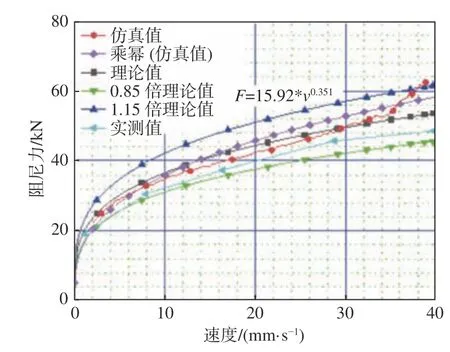
图 6 仿真、理论与试验结果的力-速度曲线（方案8）Fig.6 Force-velocity curves of simulation, theoretical and experimental results in scheme 8

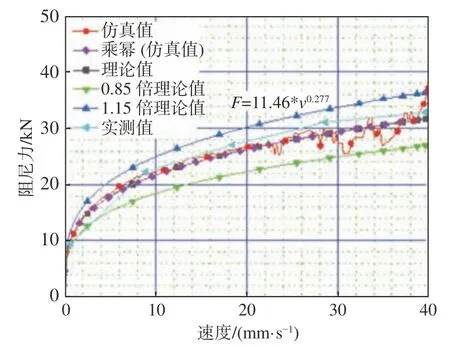
图 7 仿真、理论与试验结果的力-速度曲线（方案16）Fig.7 Force-velocity curves of simulation, theoretical and experimental results in scheme 16

由正交设计方案计算得到的仿真与理论结果如表5所示。阻尼系数仿真结果与理论结果的相对误差为±15%，速度指数仿真与理论不同，主要在于理论推导中速度指数等于黏性介质的流变指数，并且假设流体介质不可压缩，黏度不变。而仿真模拟幂律流体考虑了流体的黏度变化及可压缩性，因而会随结构的不同而发生变化。

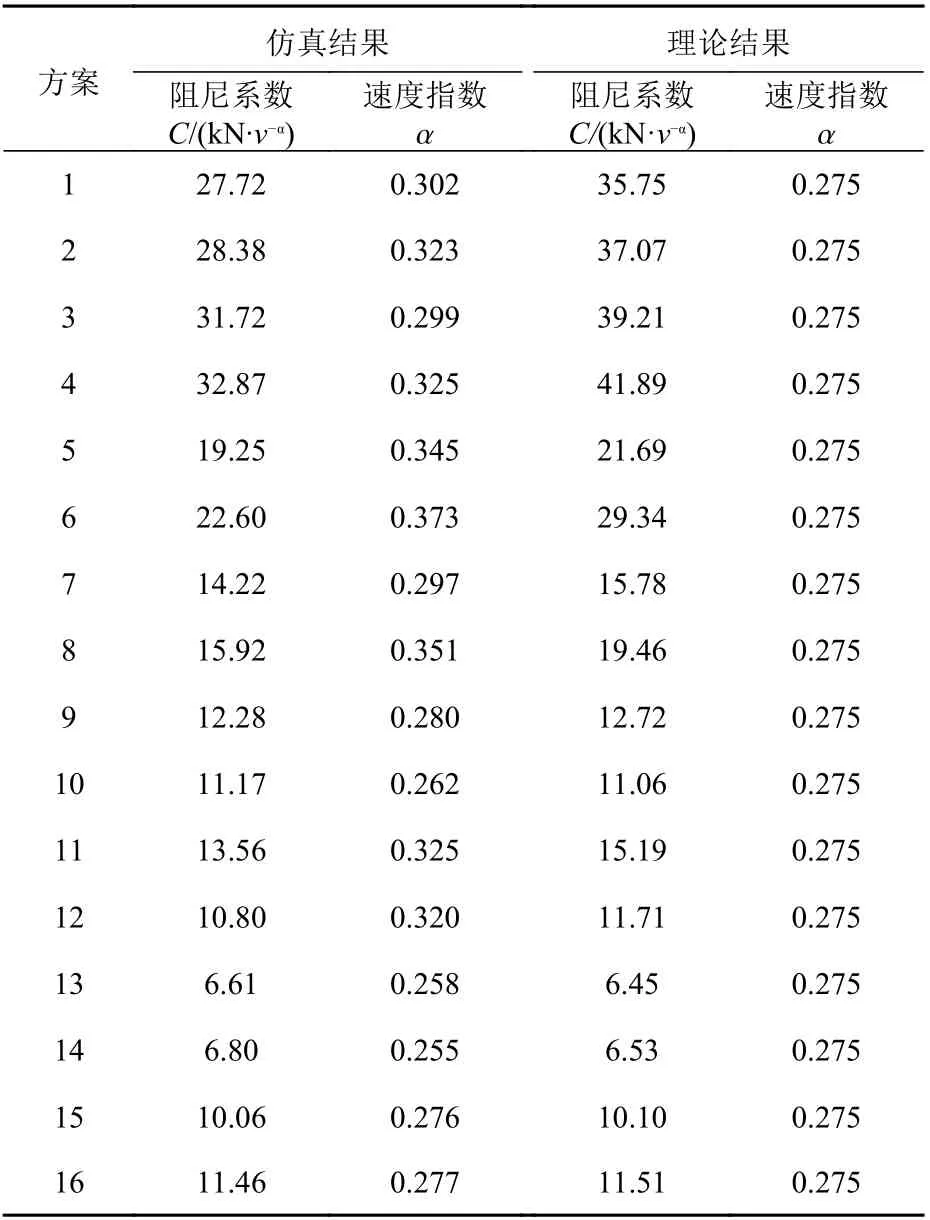
表 5 正交试验设计仿真与理论计算结果Table 5 Simulation and theoretical calculation results of orthogonal design

4.3.1 以C为评价指标的仿真结果直观分析

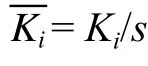
根据表6中极差的大小排列，可知各影响因素在该取值范围内对阻尼系数C的影响程度由大到小为：r0＞D1＞n＞l，其中阻尼孔半径r0为主要影响因素，空白列极差较小，可以认为各因素之间无交互作用。

4.3.2 以α为评价指标的仿真结果直观分析

以速度指数α为评价指标的仿真结果直观分析如表7所示。随其取值的变化趋势可知，在表7中的取值范围内，速度指数α是随r0的增大先增后减；随着l，D1的增大，则是先增大后减小然后再增大；随着n的增加而减小；当r0=1.5 mm，l=66 mm，n=1，D1=136 mm时，速度指数α达到最大值。同理，由表7中极差R的大小排列可知，各影响因素在表中取值范围内对速度指数α的影响作用由大到小为：r0＞n＞l＞D1，其中主要影响因素还是阻尼孔半径r0，空列极差较小可以认为是各因素之间无交互作用。

表 6 以 阻尼系数C为评价指标的直观分析Table 6 Visual analysis with the damping coefficient as the evaluation index C

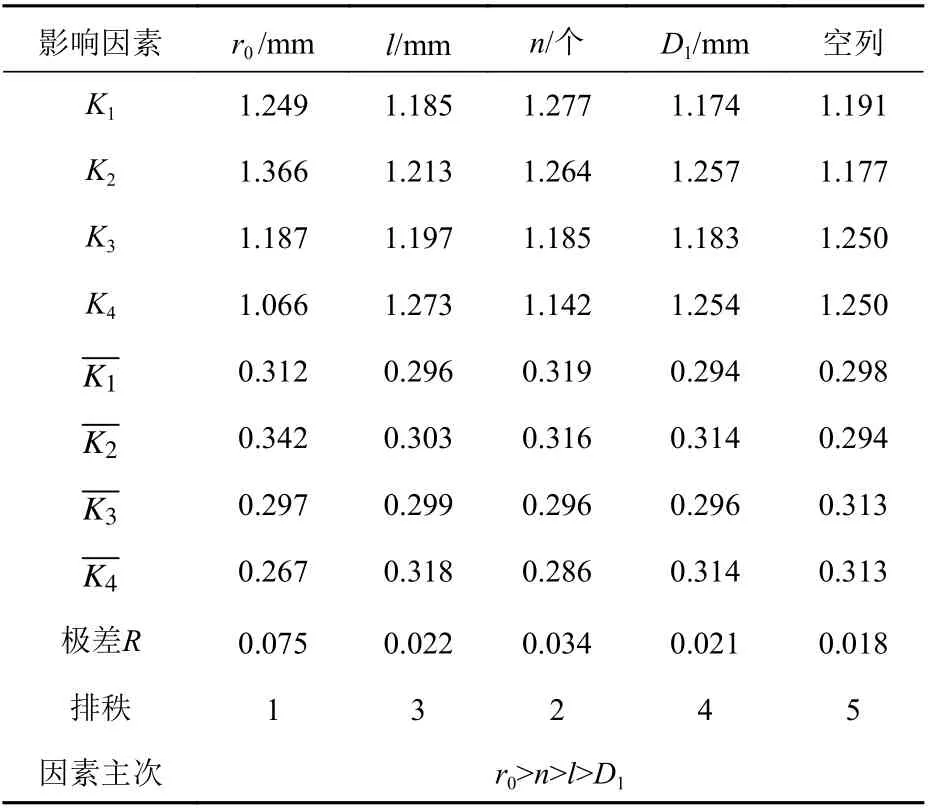
表 7 以速度指数α为评价指标的直观分析Table 7 Visual analysis with the velocity index as the evaluation index α

5 结 论

本文基于正交试验设计的思想，制定了多个VFD设计方案，建立了仿真模型，并通过FLUENT软件对VFD工作时的内部流场进行仿真计算，得到了压力和速度的分布规律及“力-速度”曲线。然后，将仿真结果和理论计算与其中3个方案的实测数据分别进行对比，验证了仿真模型的可行性，得到了r0，l，n，D1对阻尼系数C和速度指数α的影响程度，并得到如下结论：

1) 基于正交设计的仿真结果，并以VFD的阻尼系数C和速度指数α为评价指标，得到阻尼系数C的影响程度从大到小依次为r0＞D1＞n＞l，对速度指数α影响程度从大到小依次为r0＞n＞l＞D1。

2) 通过正交设计，得到各因素在该范围内评价指标达到最大的最佳组合。当r0=1.0 mm，l=66 mm，n=1，D1=136 mm时，阻尼系数C达到最大值；当r0=1.5 mm，l=66 mm，n=1，D1=136 mm时，速度指数α达到最大值。

3) 仿真计算结果与理论值和实测值的误差在±15%以内。理论计算中，VFD的速度指数α等于硅油介质的流变指数m，而由实际数值模拟的设定和结果推知，VFD的速度指数除硅油参数外还主要取决于阻尼孔的大小，故可以通过改变结构参数来改变速度指数。

4) 在本研究的基础上可对评价指标进行改进。例如，取实际值与设计值的误差作为指标，则可以通过正交设计确定评价指标最小，即与设计值最接近的设计方案。将正交设计方法应用于VFD的设计开发，可以显著减少设计方案，缩短设计周期，降低试验成本。